9.2.2 一元一次不等式的应用 课件(共18张PPT)
文档属性
| 名称 | 9.2.2 一元一次不等式的应用 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 09:02:29 | ||
图片预览






文档简介
(共18张PPT)
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
学习目标
会列一元一次不等式解决具有不等关系的实际问题.
重点:列一元一次不等式解决实际问题.
难点:寻找不等关系列出不等式,结合不等式的解集和题意,得出符合题意的解.
课前预习
阅读课本第P124-125页内容,学习本节主要内容.
设未知数
解不等式并检验解是否符合题意
答案
新课导入
有人问李老师,他所教的班级有多少名学生.李老师说:“现在正是兴趣小组活动的时间,我班一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在念外语,还剩不足6名学生在操场上踢足球.”你知道李老师班上有多少学生吗
新课导入
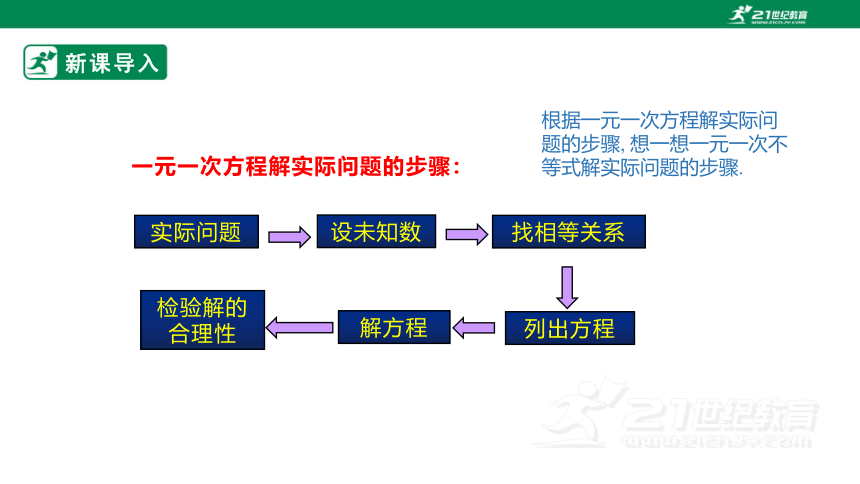
一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
根据一元一次方程解实际问题的步骤, 想一想一元一次不等式解实际问题的步骤.
例1 小明上午8时20分出发去郊游, 10时20分时, 小亮乘车从同一地点出发,已知小明每小时走4km, 那么小亮要在11时或11时前追上小明, 速度至少应是多少
新知探究
x ≥ 16.
答: 速度至少应是16km/h.
x km/h.
,
解析: 这是一个追赶问题, 读懂题意后从路程下手找不等关系. 小亮40min 行进路程要比小明从8时20分到11时行进的路程远或二者相等才可以追上. 这样可以得到不等式, 进而解决问题. 通过上述分析, 你能够通过列不等式解决这个问题吗
例1: 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比
达到60%, 如果明年(365天)这样的比值要超过70%, 那么明年空气
质量良好的天数比去年至少要增加多少
探究新知
例2: 甲、乙两商场以同样价格出售同样的商品, 并且又各自推出不同的
优惠方案: 在甲商场累计购物超过100元后, 超出100元的部分按90%
收费; 在乙商场累计购物超过50元后, 超出50元的部分按95%收费.
顾客到哪家商场购物花费少
解析: 顾客到哪家商场购物花费少, 这里有两个相关的因素: 一是顾客的购
物钱数, 二是在哪家购物. 两个商场的优惠方式是不同的, 在甲商场购
物超过100元后享受优惠, 在乙商场购物超过50元后享受优惠. 因此,
我们需要分三种情况讨论: (1)累计购物不超过50元; (2)累计购物超
过50元而不超过100元; (3)累计购物超过100元.
解: (1)当累计购物不超过50元时, 在甲、乙两商 场购物都不享受优惠, 且两商
场以同样价格出售同样的商品, 因此到两商场购物花费一样.
(2)当累计购物超过50元而不超过100元时, 享受乙商场的购物优惠, 不享受
甲商场的购物优惠,因此到乙商场购物花费少.
(3)当累计购物超过100元时, 设累计购物 x(x>100)元.
①若到甲商场购物花费少, 则50+0.95(x-50) > 100+0.9(x-100),
解得 x>150.
这就是说, 累计购物超过150元时, 到甲商场购物花费少.
②若到乙商场购物花费少, 则50+0.95(x-50) < 100+0.9(x-100),
解得 x<150.
这就是说, 累计购物超过100元而不到150元时, 到乙商场购物花费少.
③若50+0.95(x- 50)=100+0.9(x- 100), 解得x=150.
这就是说,累计购物为150元时, 到甲、乙两商场购物花费一样.
利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数, 列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
检验
数学建模
实际问题的解答
归纳总结
列一元一次不等式解实际问题与列一元一次方程解实际问题有相似之处, 一般方法步骤是 “审、设、列、解、验、答” 六步.
“审” 即审清题意, 是不需要写在纸面上的, 但一定要通过审题找出已知量和未知量, 其他五步都要写在纸面上.
“设” 是指由题意恰当地设未知数, 有直接设法和间接设法两种,因题而异;
“列” 是指找出不等关系, 列出不等式;
“解” 是指求出这个不等式的解集;
“验” 是指在不等式的解集内找到适合条件的解;
“答” 指针对题目的问题, 写出答案.
其中 “列” 是关键.
知识归纳
1.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队预计在本赛季32场比赛中至少得到48分,才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是( )
A.2x+(32-x)≥48 B.2x-(32-x)≥48
C.2x+(32-x)≤48 D.2x≥48
A
随堂练习
2.光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其他费用,结果取整数).
解:(1)设这个月的晴天有x天.
根据题意,得30x+5(30-x)=550,
解得x=16.
答:这个月晴天有16天;
(2)设y年可收回成本,根据题意,
得(550-150)×(0.52+0.45)×12y≥40 000,
解得y≥8.6.
答:至少需要9年可收回成本.
实际问题
根据题意列不等式
解一元一次不等式
根据实际问题找出符合条件的解集或整数解
得出解决问题的答案
应用一元一次不等式解决实际问题的步骤:
课堂小结
1.教材P126习题9.2第5,6,7,8题;
2.完成对应课时练习.
作业布置
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
学习目标
会列一元一次不等式解决具有不等关系的实际问题.
重点:列一元一次不等式解决实际问题.
难点:寻找不等关系列出不等式,结合不等式的解集和题意,得出符合题意的解.
课前预习
阅读课本第P124-125页内容,学习本节主要内容.
设未知数
解不等式并检验解是否符合题意
答案
新课导入
有人问李老师,他所教的班级有多少名学生.李老师说:“现在正是兴趣小组活动的时间,我班一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在念外语,还剩不足6名学生在操场上踢足球.”你知道李老师班上有多少学生吗
新课导入
一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
根据一元一次方程解实际问题的步骤, 想一想一元一次不等式解实际问题的步骤.
例1 小明上午8时20分出发去郊游, 10时20分时, 小亮乘车从同一地点出发,已知小明每小时走4km, 那么小亮要在11时或11时前追上小明, 速度至少应是多少
新知探究
x ≥ 16.
答: 速度至少应是16km/h.
x km/h.
,
解析: 这是一个追赶问题, 读懂题意后从路程下手找不等关系. 小亮40min 行进路程要比小明从8时20分到11时行进的路程远或二者相等才可以追上. 这样可以得到不等式, 进而解决问题. 通过上述分析, 你能够通过列不等式解决这个问题吗
例1: 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比
达到60%, 如果明年(365天)这样的比值要超过70%, 那么明年空气
质量良好的天数比去年至少要增加多少
探究新知
例2: 甲、乙两商场以同样价格出售同样的商品, 并且又各自推出不同的
优惠方案: 在甲商场累计购物超过100元后, 超出100元的部分按90%
收费; 在乙商场累计购物超过50元后, 超出50元的部分按95%收费.
顾客到哪家商场购物花费少
解析: 顾客到哪家商场购物花费少, 这里有两个相关的因素: 一是顾客的购
物钱数, 二是在哪家购物. 两个商场的优惠方式是不同的, 在甲商场购
物超过100元后享受优惠, 在乙商场购物超过50元后享受优惠. 因此,
我们需要分三种情况讨论: (1)累计购物不超过50元; (2)累计购物超
过50元而不超过100元; (3)累计购物超过100元.
解: (1)当累计购物不超过50元时, 在甲、乙两商 场购物都不享受优惠, 且两商
场以同样价格出售同样的商品, 因此到两商场购物花费一样.
(2)当累计购物超过50元而不超过100元时, 享受乙商场的购物优惠, 不享受
甲商场的购物优惠,因此到乙商场购物花费少.
(3)当累计购物超过100元时, 设累计购物 x(x>100)元.
①若到甲商场购物花费少, 则50+0.95(x-50) > 100+0.9(x-100),
解得 x>150.
这就是说, 累计购物超过150元时, 到甲商场购物花费少.
②若到乙商场购物花费少, 则50+0.95(x-50) < 100+0.9(x-100),
解得 x<150.
这就是说, 累计购物超过100元而不到150元时, 到乙商场购物花费少.
③若50+0.95(x- 50)=100+0.9(x- 100), 解得x=150.
这就是说,累计购物为150元时, 到甲、乙两商场购物花费一样.
利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数, 列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
检验
数学建模
实际问题的解答
归纳总结
列一元一次不等式解实际问题与列一元一次方程解实际问题有相似之处, 一般方法步骤是 “审、设、列、解、验、答” 六步.
“审” 即审清题意, 是不需要写在纸面上的, 但一定要通过审题找出已知量和未知量, 其他五步都要写在纸面上.
“设” 是指由题意恰当地设未知数, 有直接设法和间接设法两种,因题而异;
“列” 是指找出不等关系, 列出不等式;
“解” 是指求出这个不等式的解集;
“验” 是指在不等式的解集内找到适合条件的解;
“答” 指针对题目的问题, 写出答案.
其中 “列” 是关键.
知识归纳
1.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队预计在本赛季32场比赛中至少得到48分,才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是( )
A.2x+(32-x)≥48 B.2x-(32-x)≥48
C.2x+(32-x)≤48 D.2x≥48
A
随堂练习
2.光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其他费用,结果取整数).
解:(1)设这个月的晴天有x天.
根据题意,得30x+5(30-x)=550,
解得x=16.
答:这个月晴天有16天;
(2)设y年可收回成本,根据题意,
得(550-150)×(0.52+0.45)×12y≥40 000,
解得y≥8.6.
答:至少需要9年可收回成本.
实际问题
根据题意列不等式
解一元一次不等式
根据实际问题找出符合条件的解集或整数解
得出解决问题的答案
应用一元一次不等式解决实际问题的步骤:
课堂小结
1.教材P126习题9.2第5,6,7,8题;
2.完成对应课时练习.
作业布置
