勾股定理[上学期]
图片预览



文档简介
课件22张PPT。14.1勾股定理石门实验中学初二数学备课组如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?挑战难关(图中每一格代表一平方厘米)观察左图:
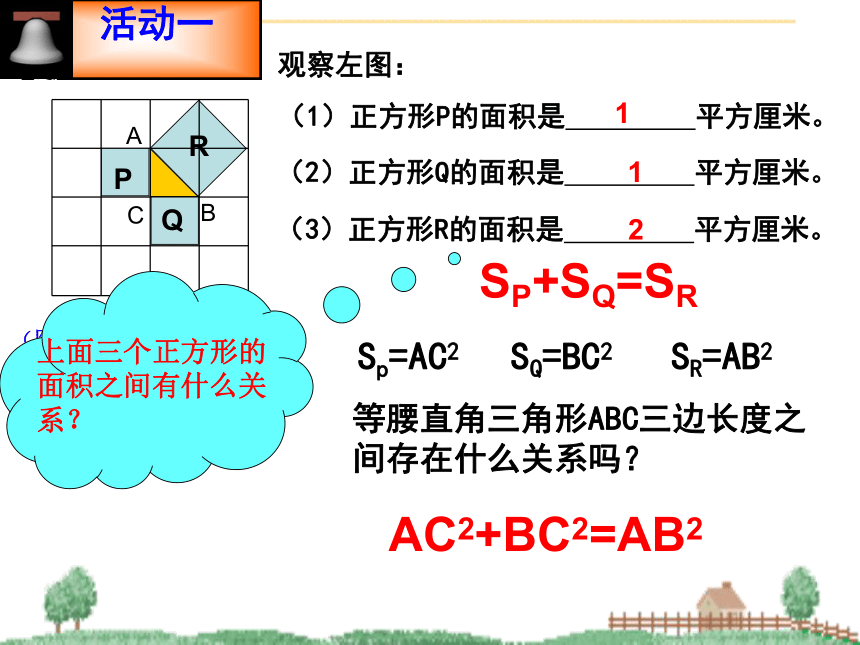
(1)正方形P的面积是 平方厘米。(2)正方形Q的面积是 平方厘米。(3)正方形R的面积是 平方厘米。121SP+SQ=SRRQPAC2+BC2=AB2等腰直角三角形ABC三边长度之间存在什么关系吗? 活动一 ? Sp=AC2 SQ=BC2 SR=AB2这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
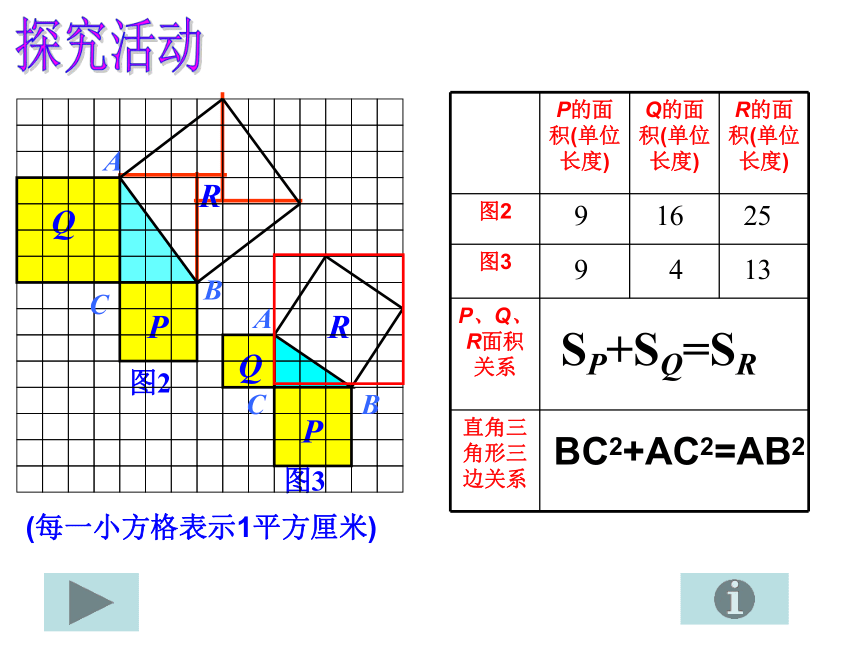
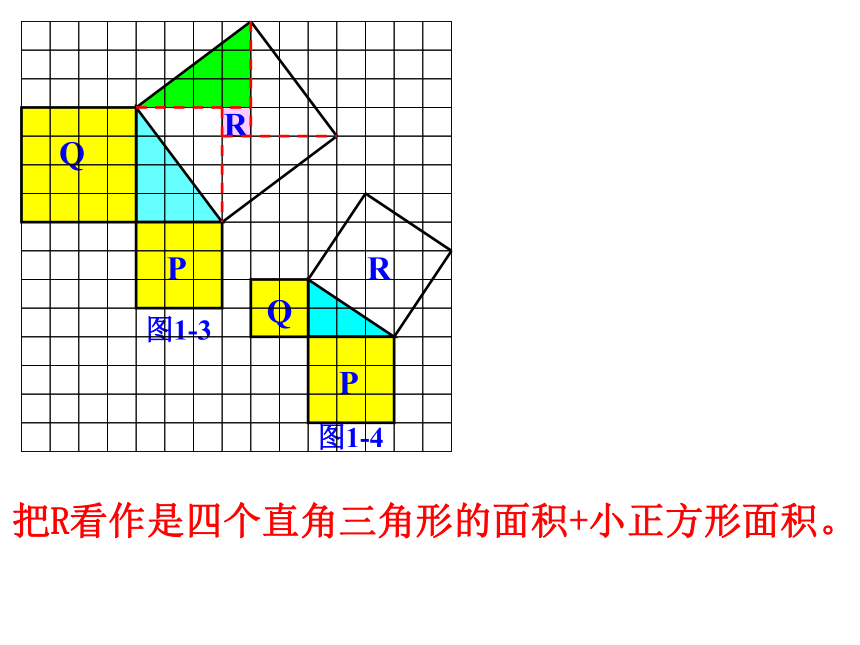
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?想一想探究活动916259413SP+SQ=SRBC2+AC2=AB2(每一小方格表示1平方厘米)把R看作是四个直角三角形的面积+小正方形面积。把R看作是大正方形面积减去四个直角三角形的面积。
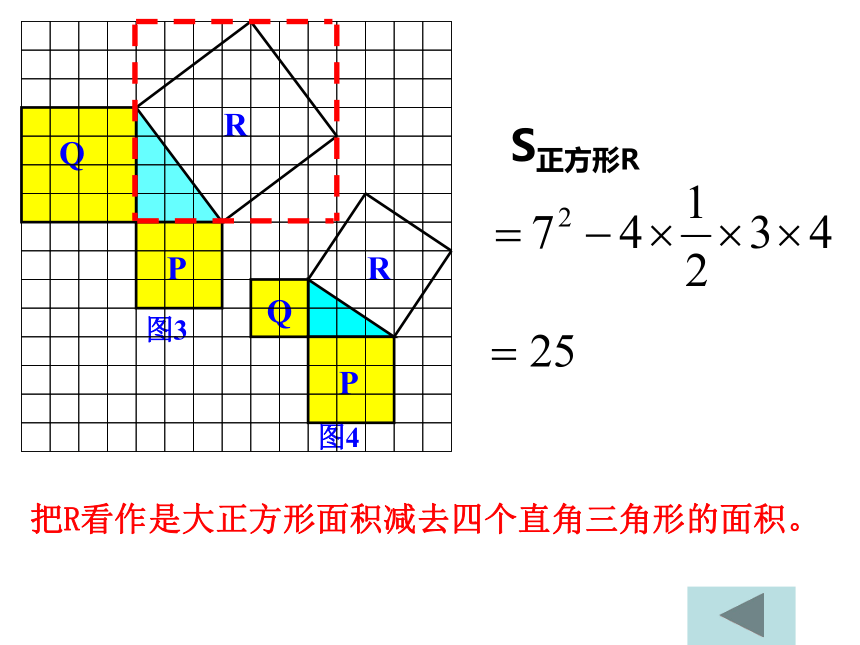
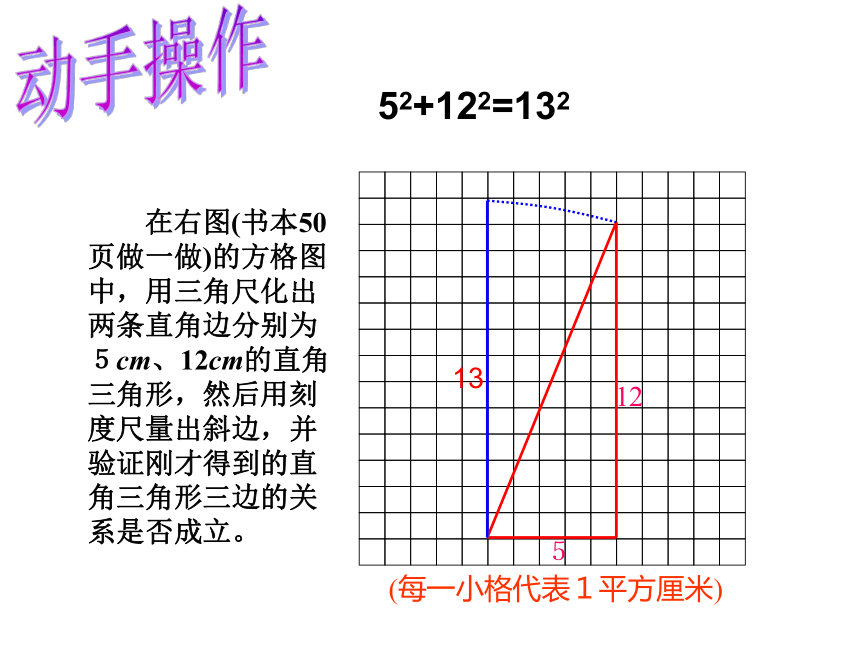
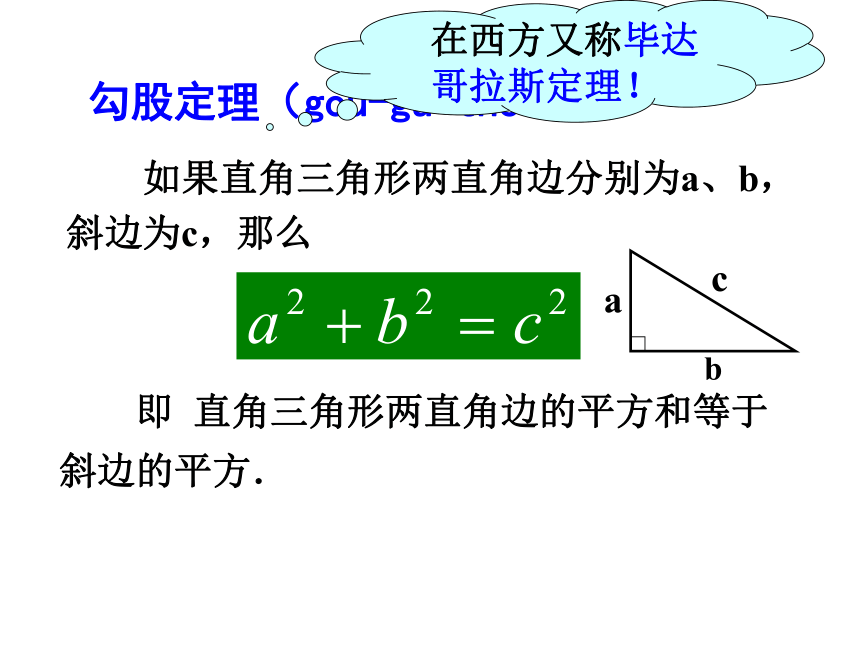
S正方形R动手操作 在右图(书本50页做一做)的方格图中,用三角尺化出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。(每一小格代表1平方厘米)51252+122=13213 勾股定理(gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?排除万难ABC课堂 练 习求出下列直角三角形中未知边的长度。6x2524x10完成同步练习卷的堂堂清、质量检测1这节课你学到了什么知识?
如果直角三角形两直角边分别为a,b,斜边为c,那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方(勾股定理)
2 你是通过什么方法得出这一结论的?小 结:3 这节课体现了哪些数学思想方法?通过数格子和割补法求面积数形相结合,从特殊到一般.再见 作业:
1、预习课本第50-53页的内容。
2、完成下节课同步练习卷的预习检测勾股定理史话 勾股定理从被发现到现在已有五千年的历史,远在公元前三千年的巴比伦人就知道和应用它了。我国古代也发现了这个定理,据《周髀算经》记载,商高(公元前1120年)关于勾股定理已有明确的认识,《周髀算经》中有商高答周公的话:“勾广三,股修四,径隅五。”同书中还有另一为学者陈子(公元前六七世纪)与荣方的一段对话:“求邪(斜)至日者,以日下为勾,日高为股,勾、股各自乘,并而开方除之,得邪(斜)至日”即
邪至日2=勾2+股2
陈子已不限于:三、四、五的特殊情形,而是推广到一般情形了。
人们对勾股定理的认识,经历过一个从特殊到一般的过程,很难区分是谁最先发明的.
勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多,1940年卢米斯收集了这个定理的370种证明,期中包括大画家达·芬奇和美国总统詹姆士·阿·加菲尔德的证法。到目前为止,已有四百多种证法.
毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 cababc证明:s总=4s1+s2①②又s总=c2赵爽弦图美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法伽菲尔德证法
剪四个完全一样的直角三角形,将他们拼成下图所示的正方形,用不同的方法表示大正方形的面积,也可以说明勾股定理的正确性
(1)正方形P的面积是 平方厘米。(2)正方形Q的面积是 平方厘米。(3)正方形R的面积是 平方厘米。121SP+SQ=SRRQPAC2+BC2=AB2等腰直角三角形ABC三边长度之间存在什么关系吗? 活动一 ? Sp=AC2 SQ=BC2 SR=AB2这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?想一想探究活动916259413SP+SQ=SRBC2+AC2=AB2(每一小方格表示1平方厘米)把R看作是四个直角三角形的面积+小正方形面积。把R看作是大正方形面积减去四个直角三角形的面积。
S正方形R动手操作 在右图(书本50页做一做)的方格图中,用三角尺化出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。(每一小格代表1平方厘米)51252+122=13213 勾股定理(gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 如图,强大的台风使得一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?排除万难ABC课堂 练 习求出下列直角三角形中未知边的长度。6x2524x10完成同步练习卷的堂堂清、质量检测1这节课你学到了什么知识?
如果直角三角形两直角边分别为a,b,斜边为c,那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方(勾股定理)
2 你是通过什么方法得出这一结论的?小 结:3 这节课体现了哪些数学思想方法?通过数格子和割补法求面积数形相结合,从特殊到一般.再见 作业:
1、预习课本第50-53页的内容。
2、完成下节课同步练习卷的预习检测勾股定理史话 勾股定理从被发现到现在已有五千年的历史,远在公元前三千年的巴比伦人就知道和应用它了。我国古代也发现了这个定理,据《周髀算经》记载,商高(公元前1120年)关于勾股定理已有明确的认识,《周髀算经》中有商高答周公的话:“勾广三,股修四,径隅五。”同书中还有另一为学者陈子(公元前六七世纪)与荣方的一段对话:“求邪(斜)至日者,以日下为勾,日高为股,勾、股各自乘,并而开方除之,得邪(斜)至日”即
邪至日2=勾2+股2
陈子已不限于:三、四、五的特殊情形,而是推广到一般情形了。
人们对勾股定理的认识,经历过一个从特殊到一般的过程,很难区分是谁最先发明的.
勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多,1940年卢米斯收集了这个定理的370种证明,期中包括大画家达·芬奇和美国总统詹姆士·阿·加菲尔德的证法。到目前为止,已有四百多种证法.
毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 cababc证明:s总=4s1+s2①②又s总=c2赵爽弦图美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法伽菲尔德证法
剪四个完全一样的直角三角形,将他们拼成下图所示的正方形,用不同的方法表示大正方形的面积,也可以说明勾股定理的正确性
