第十八章平行四边形 单元自测题 2022—2023学年华东师大版数学八年级下册(含解析)
文档属性
| 名称 | 第十八章平行四边形 单元自测题 2022—2023学年华东师大版数学八年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 550.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 16:47:22 | ||
图片预览




文档简介
华东师大版八年级数学下册 第十八章平行四边形 单元自测题
一、单选题
1.如图,四边形是平行四边形,其对角线,相交于点,下列理论一定成立的是( )
A. B. C. D.
2.下面各条件中,能判定四边形是平行四边形的是( )
A.对角线互相垂直 B.对角线互相平分 C.一组对角相等 D.一组对边相等
3.如图,在四边形中,对角线和相交于点,下列条件不能判断四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图,的对角线,交于点,若,,,则的周长为
A.14 B.17 C.18 D.19
5.若平行四边形中两内角的度数比为2:3,则其中较小的内角是( )
A. B. C. D.
6.在平行四边形ABCD中,如果,那么的度数是( )
A. B. C. D.
7.如图,已知:中,于E,,,的平分线交BC于F,连接EF.则的度数等于( )
A. B. C. D.
8.已知平行四边形中,,则等于( )
A. B. C. D.
9.如图,在平行四边形ABCD中,∠ABC的角平分线交AD于点E,∠BCD的角平分线交AD于点F,若AB=7,BC=10,则EF的长为( )
A.4 B.3 C.6 D.5
10.如图,平行四边形中的顶点O,A,C的坐标分别为,,,则顶点B的坐标为( )
A. B. C. D.
二、填空题
11.如图,在中,,若,则的度数是 .
12.如图,在平行四边形ABCD中,AC、BD相交于点O,,,,则BC的长为 .
13.如图,□ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是
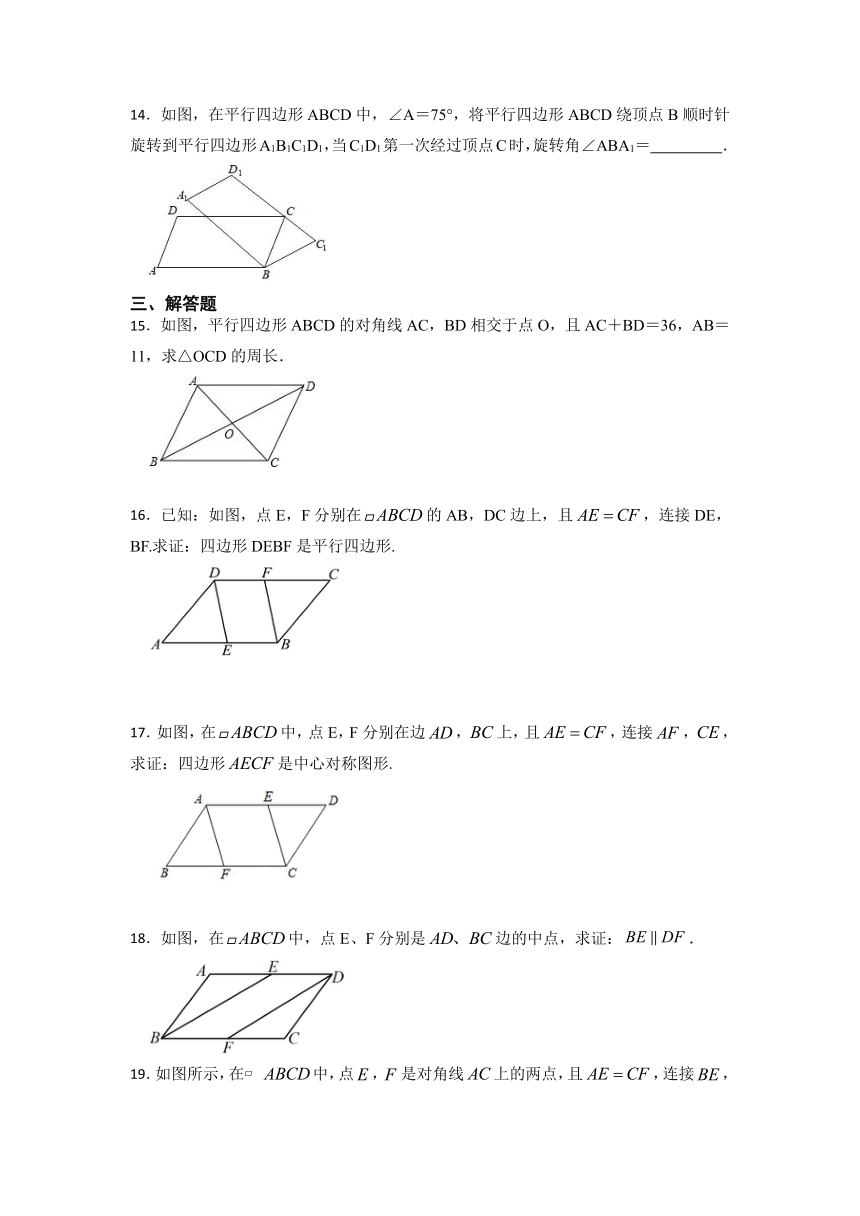
14.如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,当C1D1第一次经过顶点C时,旋转角∠ABA1= .
三、解答题
15.如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
16.已知:如图,点E,F分别在的AB,DC边上,且,连接DE,BF.求证:四边形DEBF是平行四边形.
17.如图,在中,点E,F分别在边,上,且,连接,,求证:四边形是中心对称图形.
18.如图,在中,点E、F分别是边的中点,求证:.
19.如图所示,在 中,点,是对角线上的两点,且,连接,,,求证:四边形是平行四边形.
20.如图,点P,Q是对角线上的两个点,且,顺次连接,,,.
求证:四边形是平行四边形.
四、综合题
21.如图,在四边形中,,,.
(1)用尺规完成以下基本作图:作的角平分线交于点E;(保留作图痕迹)
(2)在(1)所作的图中,证明四边形ABED是平行四边形,完成下列填空.
证明:∵.
∴① .
∵.
∴.
∵平分.
∴② .
∵.
∴③ .
∵
∴.
∴④ .
∵.
∴四边形ABED是平行四边形.
22.如图,四边形为平行四边形,为上的一点,连接并延长,使,连接并延长,使,连接.为的中点,连接.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
23.在平行四边形中,点E在边上,点F在边上,连接、、、,.
(1)如图1,求证:;
(2)如图2,设交于点G,交于点H,连接,若E是边的中点,在不添加任何辅助线的情况下,请直接写出图中以G为顶点并且与全等的所有三角形.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形是平行四边形,
∴,,,,,,
故只有选项C符合题意.
故答案为:C.
【分析】平行四边形的性质:对边平行且相等,对角线互相平分,据此判断.
2.【答案】B
【解析】【解答】解:根据对角线互相平分的四边形是平行四边形可得B正确.
故答案为:B.
【分析】利用对角线互相平分的四边形是平行四边形,可对A,B作出判断;利用有两组对角分别相等的四边形是平行四边形,可对C作出判断;利用一组对边平行且相等的四边形是平行四边形,可对D作出判断.
3.【答案】D
【解析】【解答】解: A 、 ∵AB∥DC , AD∥BC ,
四边形ABCD是平行四边形,故选项A不符合题意;
B、 , ,
四边形ABCD是平行四边形,故选项A不符合题意;
C、 , ,
四边形ABCD是平行四边形,故选项A不符合题意;
D、 ∵AB∥DC , AD=BC ,
四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
故答案为:D.
【分析】平行四边形的判定:两条对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形,据此一一判断得出答案.
4.【答案】D
【解析】【解答】解: 四边形ABCD是平行四边形,
, , ,
∴△ABC的周长 ,
故答案为:D.
【分析】由平行四边形的性质可得,,,根据△OBC的周长=BC+OC+OB即可求解.
5.【答案】D
【解析】【解答】解:如图,设,,
四边形ABCD是平行四边形,
,
,
,
解得:,
,
即其中较小的内角是,
故答案为:D.
【分析】如图,设∠A=3x,∠B=2x,由平行四边形的邻角互补可得∠A+∠B=180°,于是可得关于x的方程,解方程可求解.
6.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形,,
∴,
故答案为:D
【分析】根据平行四边形的性质,结合求解即可。
7.【答案】C
【解析】【解答】解:∵中,,
∴,
∵,
∴,
∵的平分线交BC于F,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:C.
【分析】先求出,可得,再结合,可得,利用等腰三角形的内角和求出,再利用角的运算求出即可。
8.【答案】D
【解析】【解答】解:∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∴.
故答案为:D.
【分析】利用平行四边形的性质可得,再结合,求出即可。
9.【答案】A
【解析】【解答】解:∵平行四边形ABCD,
∴AD∥BC,
∴∠DFC=∠FCB,
又CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证:AE=AB,
∵AB=7,AD=BC=10,
∴EF=AE+FD-AD=2AB-BC=4.
故答案为:A.
【分析】根据角平分线的定义及平行线的性质证出∠DFC=∠DCF,可得DF=DC,AE=AB,再利用线段的和差及等量代换求出EF的长即可。
10.【答案】D
【解析】【解答】解:在中,,A,,
∴,
又∵,
∴点B的纵坐标与点A的纵坐标相等,
∴,故D符合题意.
故答案为:D.
【分析】利用平行四边形的性质可得,再结合点B的纵坐标与点A的纵坐标相等,即可得到,从而得解。
11.【答案】40°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:40°.
【分析】由平行四边形的对边平行得AD∥BC,进而根据二直线平行,内错角相等得∠CAD=∠ACB,进而根据三角形的内角和算出∠ACB的度数即可.
12.【答案】4
【解析】【解答】解:∵四边形ABCD是平行四边形,AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3,,
∵∠ODA=90°,
∴在Rt△ADO中,由勾股定理可知,,
∴.
故答案为:4.
【分析】利用勾股定理求出AD的长,再利用平行四边形的性质可得。
13.【答案】20
【解析】【解答】解:四边形是平行四边形,
,,,
,
,
的周长为10,
即,
平行四边形的周长为:
.
故答案为:20.
【分析】根据平行四边形的性质可得,,,再利用三角形的周长公式可得,最后利用平行四边形的周长公式及等量代换可得答案。
14.【答案】30°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠BCD=75°,
∵将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,
∴∠ABA1=∠CBC1,BC=BC1,∠C1=∠BCD=75°,
∴∠C1=∠BCC1=75°,
∠CBC1=∠ABA1=180°-75°-75°=30°.
故答案为:30°
【分析】利用平行四边形的性质可求出∠BCD的度数,利用旋转的性质可得到∠ABA1=∠CBC1,BC=BC1,∠C1=∠BCD=75°,利用等边对等角可证得∠C1=∠BCC1=75°,然后利用三角形的内角和定理求出结果.
15.【答案】解:∵ABCD是平行四边形,
∴AB=CD=11,,,
∵AC+BD=36,
∴,
∴△OCD的周长=OC+OD+CD=18+11=29.
【解析】【分析】根据平行四边形的性质可得,再利用三角形的周长公式计算即可。
16.【答案】证明:四边形ABCD是平行四边形,
,
,
,
四边形DEBF是平行四边形.
【解析】【分析】根据平行四边形的性质可得AB=CD,AB∥CD,由已知条件知AE=CF,结合线段的和差关系可得BE=DF,然后根据一组对边平行且相等的四边形是平行四边形进行证明.
17.【答案】证明:四边形是平行四边形,
,,
四边形是平行四边形,
四边形是中心对称图形.
【解析】【分析】根据平行四边形的性质可得AD∥BC,由已知条件可知AE=CF,推出四边形AECF为平行四边形,据此证明.
18.【答案】证明:∵四边形是平行四边形,
∴,
∵点E、F分别是边的中点,
∴
∴,
∴四边形是平行四边形,
∴.
【解析】【分析】先证明四边形是平行四边形, 再利用平行四边形的性质可得。
19.【答案】证明:连接,交于点,如图.
四边形是平行四边形,
,平行四边形的对角线互相平分.
,,
,即,
四边形是平行四边形对角线互相平分的四边形是平行四边形.
【解析】【分析】连接BD,交AC于点O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,结合AE=CF,根据线段的和差关系可得OE=OF,然后根据平行四边形的判定定理(对角线互相平分的四边形是平行四边形)进行证明.
20.【答案】证明:连接交于点O,
∵四边形是平行四边形,
,,
,
,
即,
,
∴四边形是平行四边形.
【解析】【分析】利用对角线互相平分的四边形是平行四边形证明即可。
21.【答案】(1)解:如图,即为所求;
;
(2)证明:∵.
∴.
∵.
∴.
∵平分.
∴.
∵.
∴.
∵
∴.
∴.
∵.
∴四边形ABED是平行四边形.
故答案为:①;②;③;④.
【解析】【分析】(1)利用角平分线的作法,利用尺规作图作出∠ABC的角平分线,交CD于点E.
(2)利用平行线的性质可证得∠ABE=∠BEC,同时可求出∠ABC的度数;再利用角平分线的定义求出∠ABE的度数;利用平行线的性质求出∠BEC的度数,可推出∠D=∠BEC,利用平行线的判定定理可得AD∥BE,利用有两组对边分别平行的四边形是平行四边形,可证得四边形ABED是平行四边形.
22.【答案】(1)证明:四边形是平行四边形,
,,
,,
是的中位线,
,,
为的中点,
,
,,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
,
,
,
,
.
【解析】【分析】(1)先证明,再结合AD=FH,可得四边形是平行四边形;
(2)根据平行四边形的性质可得,利用角的运算求出,再利用三角形的内角和及等腰三角形的性质可得。
23.【答案】(1)证明:∵四边形是平行四边形,
∴,.
∵,
∴.
∴.
(2)解:以为顶点的三角形且与全等的三角形有:,,,.
【解析】【解答】(2)解:∵E是的中点,
∴.
∵,
∴.
∵四边形是平行四边形,
∴,.
∴.
∴.
∴.
∵,
∴,,
∴,
∴,,
同理可得:,,
∴,,
∴四边形是平行四边形,四边形是平行四边形,四边形是平行四边形.
由平行四边形的中心对称的性质可得:以为顶点的三角形且与全等的三角形有:,,,.
【分析】(1)先利用“ASA”证明,再利用全等三角形的性质可得;
(2)利用全等三角形的判定方法求解即可。
一、单选题
1.如图,四边形是平行四边形,其对角线,相交于点,下列理论一定成立的是( )
A. B. C. D.
2.下面各条件中,能判定四边形是平行四边形的是( )
A.对角线互相垂直 B.对角线互相平分 C.一组对角相等 D.一组对边相等
3.如图,在四边形中,对角线和相交于点,下列条件不能判断四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图,的对角线,交于点,若,,,则的周长为
A.14 B.17 C.18 D.19
5.若平行四边形中两内角的度数比为2:3,则其中较小的内角是( )
A. B. C. D.
6.在平行四边形ABCD中,如果,那么的度数是( )
A. B. C. D.
7.如图,已知:中,于E,,,的平分线交BC于F,连接EF.则的度数等于( )
A. B. C. D.
8.已知平行四边形中,,则等于( )
A. B. C. D.
9.如图,在平行四边形ABCD中,∠ABC的角平分线交AD于点E,∠BCD的角平分线交AD于点F,若AB=7,BC=10,则EF的长为( )
A.4 B.3 C.6 D.5
10.如图,平行四边形中的顶点O,A,C的坐标分别为,,,则顶点B的坐标为( )
A. B. C. D.
二、填空题
11.如图,在中,,若,则的度数是 .
12.如图,在平行四边形ABCD中,AC、BD相交于点O,,,,则BC的长为 .
13.如图,□ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是
14.如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,当C1D1第一次经过顶点C时,旋转角∠ABA1= .
三、解答题
15.如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
16.已知:如图,点E,F分别在的AB,DC边上,且,连接DE,BF.求证:四边形DEBF是平行四边形.
17.如图,在中,点E,F分别在边,上,且,连接,,求证:四边形是中心对称图形.
18.如图,在中,点E、F分别是边的中点,求证:.
19.如图所示,在 中,点,是对角线上的两点,且,连接,,,求证:四边形是平行四边形.
20.如图,点P,Q是对角线上的两个点,且,顺次连接,,,.
求证:四边形是平行四边形.
四、综合题
21.如图,在四边形中,,,.
(1)用尺规完成以下基本作图:作的角平分线交于点E;(保留作图痕迹)
(2)在(1)所作的图中,证明四边形ABED是平行四边形,完成下列填空.
证明:∵.
∴① .
∵.
∴.
∵平分.
∴② .
∵.
∴③ .
∵
∴.
∴④ .
∵.
∴四边形ABED是平行四边形.
22.如图,四边形为平行四边形,为上的一点,连接并延长,使,连接并延长,使,连接.为的中点,连接.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
23.在平行四边形中,点E在边上,点F在边上,连接、、、,.
(1)如图1,求证:;
(2)如图2,设交于点G,交于点H,连接,若E是边的中点,在不添加任何辅助线的情况下,请直接写出图中以G为顶点并且与全等的所有三角形.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形是平行四边形,
∴,,,,,,
故只有选项C符合题意.
故答案为:C.
【分析】平行四边形的性质:对边平行且相等,对角线互相平分,据此判断.
2.【答案】B
【解析】【解答】解:根据对角线互相平分的四边形是平行四边形可得B正确.
故答案为:B.
【分析】利用对角线互相平分的四边形是平行四边形,可对A,B作出判断;利用有两组对角分别相等的四边形是平行四边形,可对C作出判断;利用一组对边平行且相等的四边形是平行四边形,可对D作出判断.
3.【答案】D
【解析】【解答】解: A 、 ∵AB∥DC , AD∥BC ,
四边形ABCD是平行四边形,故选项A不符合题意;
B、 , ,
四边形ABCD是平行四边形,故选项A不符合题意;
C、 , ,
四边形ABCD是平行四边形,故选项A不符合题意;
D、 ∵AB∥DC , AD=BC ,
四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
故答案为:D.
【分析】平行四边形的判定:两条对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形,据此一一判断得出答案.
4.【答案】D
【解析】【解答】解: 四边形ABCD是平行四边形,
, , ,
∴△ABC的周长 ,
故答案为:D.
【分析】由平行四边形的性质可得,,,根据△OBC的周长=BC+OC+OB即可求解.
5.【答案】D
【解析】【解答】解:如图,设,,
四边形ABCD是平行四边形,
,
,
,
解得:,
,
即其中较小的内角是,
故答案为:D.
【分析】如图,设∠A=3x,∠B=2x,由平行四边形的邻角互补可得∠A+∠B=180°,于是可得关于x的方程,解方程可求解.
6.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形,,
∴,
故答案为:D
【分析】根据平行四边形的性质,结合求解即可。
7.【答案】C
【解析】【解答】解:∵中,,
∴,
∵,
∴,
∵的平分线交BC于F,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:C.
【分析】先求出,可得,再结合,可得,利用等腰三角形的内角和求出,再利用角的运算求出即可。
8.【答案】D
【解析】【解答】解:∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∴.
故答案为:D.
【分析】利用平行四边形的性质可得,再结合,求出即可。
9.【答案】A
【解析】【解答】解:∵平行四边形ABCD,
∴AD∥BC,
∴∠DFC=∠FCB,
又CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证:AE=AB,
∵AB=7,AD=BC=10,
∴EF=AE+FD-AD=2AB-BC=4.
故答案为:A.
【分析】根据角平分线的定义及平行线的性质证出∠DFC=∠DCF,可得DF=DC,AE=AB,再利用线段的和差及等量代换求出EF的长即可。
10.【答案】D
【解析】【解答】解:在中,,A,,
∴,
又∵,
∴点B的纵坐标与点A的纵坐标相等,
∴,故D符合题意.
故答案为:D.
【分析】利用平行四边形的性质可得,再结合点B的纵坐标与点A的纵坐标相等,即可得到,从而得解。
11.【答案】40°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:40°.
【分析】由平行四边形的对边平行得AD∥BC,进而根据二直线平行,内错角相等得∠CAD=∠ACB,进而根据三角形的内角和算出∠ACB的度数即可.
12.【答案】4
【解析】【解答】解:∵四边形ABCD是平行四边形,AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3,,
∵∠ODA=90°,
∴在Rt△ADO中,由勾股定理可知,,
∴.
故答案为:4.
【分析】利用勾股定理求出AD的长,再利用平行四边形的性质可得。
13.【答案】20
【解析】【解答】解:四边形是平行四边形,
,,,
,
,
的周长为10,
即,
平行四边形的周长为:
.
故答案为:20.
【分析】根据平行四边形的性质可得,,,再利用三角形的周长公式可得,最后利用平行四边形的周长公式及等量代换可得答案。
14.【答案】30°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠BCD=75°,
∵将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,
∴∠ABA1=∠CBC1,BC=BC1,∠C1=∠BCD=75°,
∴∠C1=∠BCC1=75°,
∠CBC1=∠ABA1=180°-75°-75°=30°.
故答案为:30°
【分析】利用平行四边形的性质可求出∠BCD的度数,利用旋转的性质可得到∠ABA1=∠CBC1,BC=BC1,∠C1=∠BCD=75°,利用等边对等角可证得∠C1=∠BCC1=75°,然后利用三角形的内角和定理求出结果.
15.【答案】解:∵ABCD是平行四边形,
∴AB=CD=11,,,
∵AC+BD=36,
∴,
∴△OCD的周长=OC+OD+CD=18+11=29.
【解析】【分析】根据平行四边形的性质可得,再利用三角形的周长公式计算即可。
16.【答案】证明:四边形ABCD是平行四边形,
,
,
,
四边形DEBF是平行四边形.
【解析】【分析】根据平行四边形的性质可得AB=CD,AB∥CD,由已知条件知AE=CF,结合线段的和差关系可得BE=DF,然后根据一组对边平行且相等的四边形是平行四边形进行证明.
17.【答案】证明:四边形是平行四边形,
,,
四边形是平行四边形,
四边形是中心对称图形.
【解析】【分析】根据平行四边形的性质可得AD∥BC,由已知条件可知AE=CF,推出四边形AECF为平行四边形,据此证明.
18.【答案】证明:∵四边形是平行四边形,
∴,
∵点E、F分别是边的中点,
∴
∴,
∴四边形是平行四边形,
∴.
【解析】【分析】先证明四边形是平行四边形, 再利用平行四边形的性质可得。
19.【答案】证明:连接,交于点,如图.
四边形是平行四边形,
,平行四边形的对角线互相平分.
,,
,即,
四边形是平行四边形对角线互相平分的四边形是平行四边形.
【解析】【分析】连接BD,交AC于点O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,结合AE=CF,根据线段的和差关系可得OE=OF,然后根据平行四边形的判定定理(对角线互相平分的四边形是平行四边形)进行证明.
20.【答案】证明:连接交于点O,
∵四边形是平行四边形,
,,
,
,
即,
,
∴四边形是平行四边形.
【解析】【分析】利用对角线互相平分的四边形是平行四边形证明即可。
21.【答案】(1)解:如图,即为所求;
;
(2)证明:∵.
∴.
∵.
∴.
∵平分.
∴.
∵.
∴.
∵
∴.
∴.
∵.
∴四边形ABED是平行四边形.
故答案为:①;②;③;④.
【解析】【分析】(1)利用角平分线的作法,利用尺规作图作出∠ABC的角平分线,交CD于点E.
(2)利用平行线的性质可证得∠ABE=∠BEC,同时可求出∠ABC的度数;再利用角平分线的定义求出∠ABE的度数;利用平行线的性质求出∠BEC的度数,可推出∠D=∠BEC,利用平行线的判定定理可得AD∥BE,利用有两组对边分别平行的四边形是平行四边形,可证得四边形ABED是平行四边形.
22.【答案】(1)证明:四边形是平行四边形,
,,
,,
是的中位线,
,,
为的中点,
,
,,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
,
,
,
,
.
【解析】【分析】(1)先证明,再结合AD=FH,可得四边形是平行四边形;
(2)根据平行四边形的性质可得,利用角的运算求出,再利用三角形的内角和及等腰三角形的性质可得。
23.【答案】(1)证明:∵四边形是平行四边形,
∴,.
∵,
∴.
∴.
(2)解:以为顶点的三角形且与全等的三角形有:,,,.
【解析】【解答】(2)解:∵E是的中点,
∴.
∵,
∴.
∵四边形是平行四边形,
∴,.
∴.
∴.
∴.
∵,
∴,,
∴,
∴,,
同理可得:,,
∴,,
∴四边形是平行四边形,四边形是平行四边形,四边形是平行四边形.
由平行四边形的中心对称的性质可得:以为顶点的三角形且与全等的三角形有:,,,.
【分析】(1)先利用“ASA”证明,再利用全等三角形的性质可得;
(2)利用全等三角形的判定方法求解即可。
