勾股定理2[上学期]
图片预览






文档简介
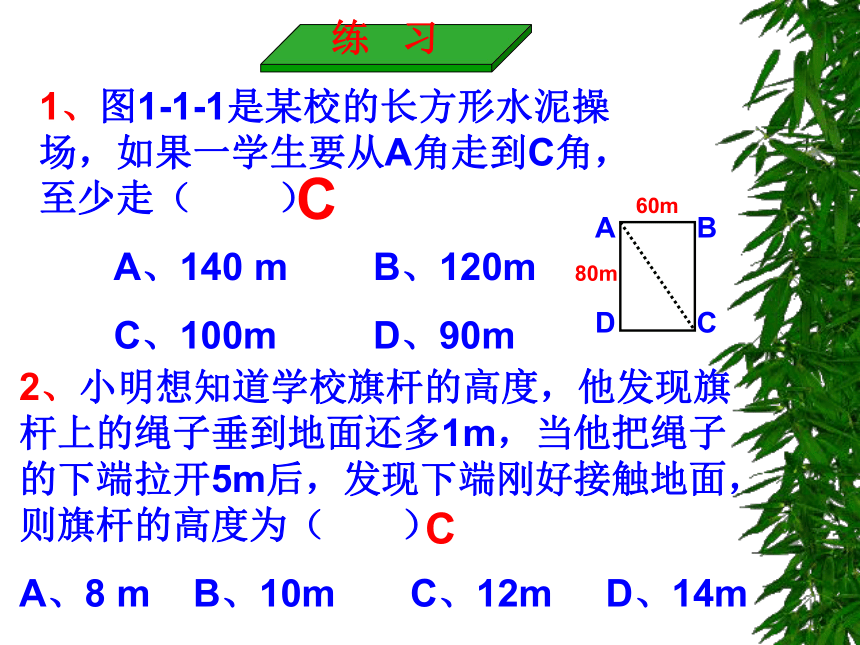
课件17张PPT。14.1.2勾股定理 练 习1、图1-1-1是某校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
A、140 m B、120m
C、100m D、90mCC2、小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高度为( )
A、8 m B、10m C、12m D、14m3、现有一长5m的梯子,架靠在建筑物的墙上,它们的底部在地面的水平距离是3m,则梯子可以到达建筑物的高度是_______;
4、在Rt△ABC中,斜边AB=2,
则AB2+BC2+CA2=_______;
5、在直角三角形中,一条直角边长为11cm,另两边是两个连续自然数,则此三角形的周长为_____。4m8132例1.在Rt?ABC中,AB=c,BC=a,AC=b,?B=90? (1)已知a=6,b=10,求c; (2)已知a=24,c=25,求b.解:在Rt?ABC中,?B=90?,
根据勾股定理,有a2+c2=b2例2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?设斜边长为xcm,根据勾股定理,得=5设另一直角边长为ycm,根据勾股定理,得ABC34ABC34合作探究为了求出湖两岸A,B两点之间的距离,动动脑筋用你学过的知识来解决吧?我相信你一定能成功!例3、如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米。问从点A穿过湖到点B有多远?解:在Rt△ABC中,∠B=90°,AC=160米,BC=128米,根据勾股定理,得= 96(米)答:从点A穿过湖到点B有96米。 葭生池中 今有方池一丈, 葭生其中央, 出水一尺, 引葭赴岸, 适与岸齐。 问:水深、葭长各几何? X-1X1尺解:可设葭长为x尺,则水深为(x-1)尺。则有: (x-1)2+52=x2解得:x=13所以:葭长13尺,水深12尺。葭(jiā) 本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?1.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?C解:在Rt△ABC中,∠ACB=90°AC=6,BC=8,根据勾股定理,得AB ===10(千米)答:登陆点A到宝藏点B的直线距离是10千米。过点B作BC⊥AC于CDA2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,则a,b,c为
基本勾股数.如:3、4、5 ; 5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数
勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2你能用一块砖推倒的过程证明《勾股定理》吗?提示:表示出梯形的面积
设AC=a AB=b
BC=c美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法伽菲尔德证法
A、140 m B、120m
C、100m D、90mCC2、小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高度为( )
A、8 m B、10m C、12m D、14m3、现有一长5m的梯子,架靠在建筑物的墙上,它们的底部在地面的水平距离是3m,则梯子可以到达建筑物的高度是_______;
4、在Rt△ABC中,斜边AB=2,
则AB2+BC2+CA2=_______;
5、在直角三角形中,一条直角边长为11cm,另两边是两个连续自然数,则此三角形的周长为_____。4m8132例1.在Rt?ABC中,AB=c,BC=a,AC=b,?B=90? (1)已知a=6,b=10,求c; (2)已知a=24,c=25,求b.解:在Rt?ABC中,?B=90?,
根据勾股定理,有a2+c2=b2例2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?设斜边长为xcm,根据勾股定理,得=5设另一直角边长为ycm,根据勾股定理,得ABC34ABC34合作探究为了求出湖两岸A,B两点之间的距离,动动脑筋用你学过的知识来解决吧?我相信你一定能成功!例3、如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米。问从点A穿过湖到点B有多远?解:在Rt△ABC中,∠B=90°,AC=160米,BC=128米,根据勾股定理,得= 96(米)答:从点A穿过湖到点B有96米。 葭生池中 今有方池一丈, 葭生其中央, 出水一尺, 引葭赴岸, 适与岸齐。 问:水深、葭长各几何? X-1X1尺解:可设葭长为x尺,则水深为(x-1)尺。则有: (x-1)2+52=x2解得:x=13所以:葭长13尺,水深12尺。葭(jiā) 本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?1.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?C解:在Rt△ABC中,∠ACB=90°AC=6,BC=8,根据勾股定理,得AB ===10(千米)答:登陆点A到宝藏点B的直线距离是10千米。过点B作BC⊥AC于CDA2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,则a,b,c为
基本勾股数.如:3、4、5 ; 5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数
勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2你能用一块砖推倒的过程证明《勾股定理》吗?提示:表示出梯形的面积
设AC=a AB=b
BC=c美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法伽菲尔德证法
