勾股定理习题课[上学期]
图片预览




文档简介
课件10张PPT。1.在Rt?ABC中,AB=c,BC=a,AC=b,?B=90?.
(1)已知a=6,b=10,求c;
(2)已知a=24,c=25,求b.2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么
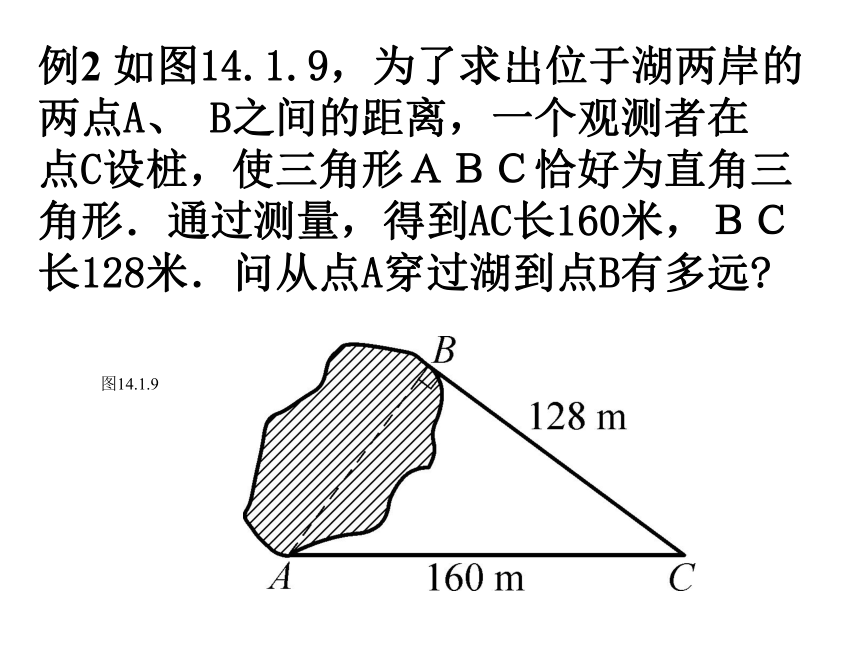
这个三角形的周长是多少厘米?练一练解:在Rt?ABC中,?C=90?,ABC34DABC34D 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?想一想:∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396例2 如图14.1.9,为了求出位于湖两岸的
两点A、 B之间的距离,一个观测者在
点C设桩,使三角形ABC恰好为直角三
角形.通过测量,得到AC长160米,BC
长128米.问从点A穿过湖到点B有多远?
图14.1.9解 如图14.1.9,在直角三角形ABC中,AC=160米, BC=128米,
根据勾股定理可得
AB===96(米).
答: 从点A穿过湖到点B有96米. 例.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
如图,小方格都是边长为1的正方
形,求四边形ABCD的面积与周长 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水截面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.?6841?244.8在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。
(1)已知a=6,b=10,求c;
(2)已知a=24,c=25,求b.2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么
这个三角形的周长是多少厘米?练一练解:在Rt?ABC中,?C=90?,ABC34DABC34D 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?想一想:∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396例2 如图14.1.9,为了求出位于湖两岸的
两点A、 B之间的距离,一个观测者在
点C设桩,使三角形ABC恰好为直角三
角形.通过测量,得到AC长160米,BC
长128米.问从点A穿过湖到点B有多远?
图14.1.9解 如图14.1.9,在直角三角形ABC中,AC=160米, BC=128米,
根据勾股定理可得
AB===96(米).
答: 从点A穿过湖到点B有96米. 例.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
如图,小方格都是边长为1的正方
形,求四边形ABCD的面积与周长 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水截面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.?6841?244.8在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。
