探索勾股定理[上学期]
图片预览





文档简介
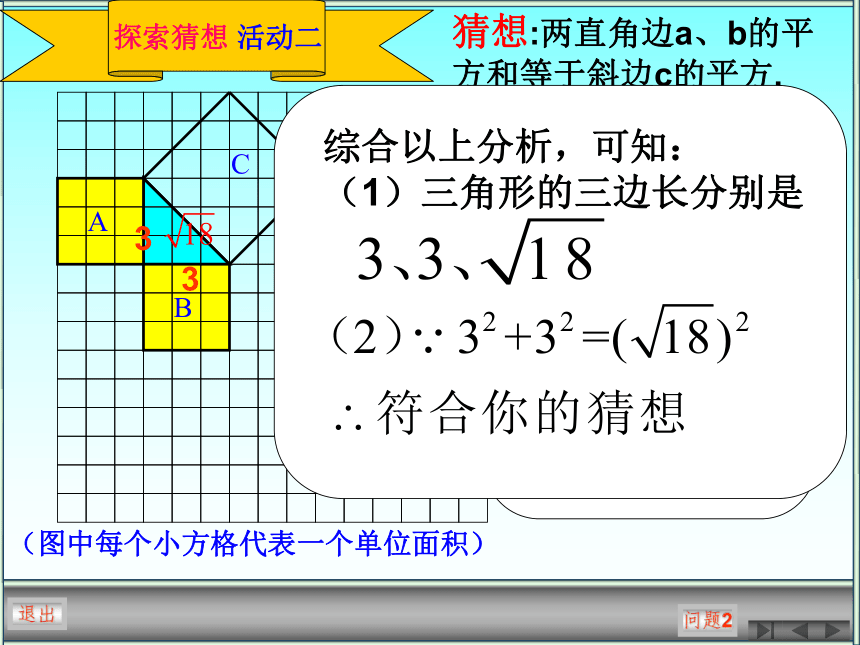
课件14张PPT。探索勾股定理退出(图中每个小方格代表一个单位面积)退出演示+=+=探索猜想 活动一看图思考:直角三角形各边是多少?由此你能得出什么猜想?即:+=91625猜想:两直角边a、b的平方和等于斜边c的平方.(图中每个小方格代表一个单位面积)探索猜想 活动二退出问题2想一想:(1)图
中的正方形C的面
积是多少?你是怎
样得到的?
(2)直角三角形
的边长各是多少?
符合你的猜想吗?33猜想:两直角边a、b的平方和等于斜边c的平方.探索猜想 活动三1分割法添补法退出分割法添补法猜想猜想:两直角边a、b的平方
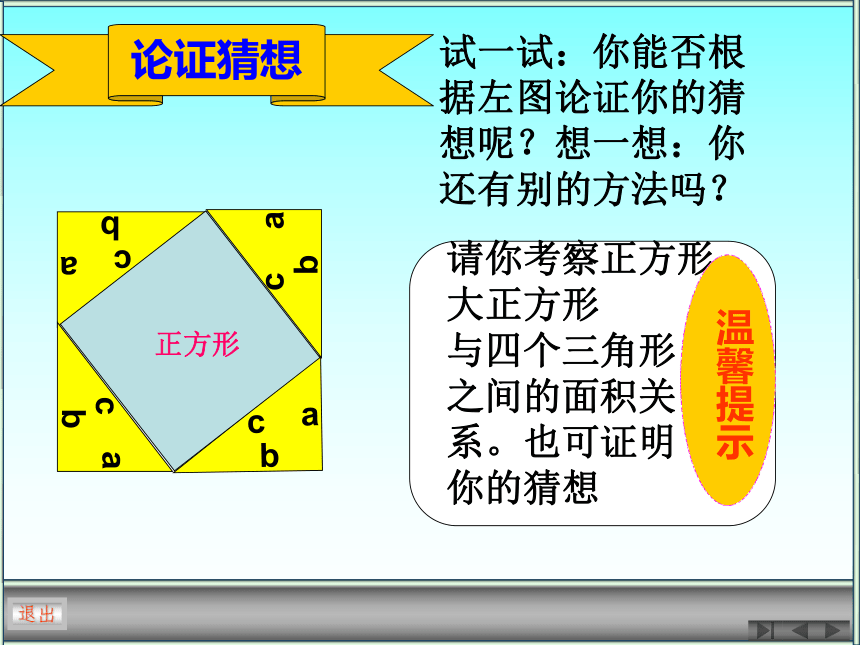
和等于斜边c的平方.退出论证猜想左图叫做玄图。是由四个相同的直角三角形拼成的。
如何证明我们的猜想呢?答案就在左图中小正方形退出退出演示论证猜想+=+=如何证明你的猜想呢?退出论证猜想正方形试一试:你能否根据左图论证你的猜想呢?想一想:你还有别的方法吗?退出 勾股定理(gou-gu theorem)勾股弦变式 在直角三角形中,两条直角边的平方和等于斜边的平方 即退出例题解析解答应用退出延伸题练习2 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长。(只考虑解法)ABCD添补分割法添补法43211234分割温馨提示:
利用勾股定理
两种方法:分割法和添补法退出温馨提示:可以考虑
构造直角三角形,过
B点作垂线BC,垂足为C点,则三角形ABC为
直角三角形,如图
所示,BC=6+2=8,
AC=8-2=6,退出练习3 (课本53页练习
第二题)求AB的距离.AB提高题演示退出本课小结谈谈你的收获小结3小结2小结1退出勾股史话★勾股定理迄今为止已有五千年历史。我国古代早在公元前1120年于著名的《周髀算经》中就已将勾股定理推广到一般情形了。
★ 《毕氏命题》搜集了370多种证明方法,包括大画家达芬奇和美国第二十任总统的证法
★美丽的勾股树
你一定见过多姿多彩的树木,可是你是否见过
美丽的勾股树呢?
中的正方形C的面
积是多少?你是怎
样得到的?
(2)直角三角形
的边长各是多少?
符合你的猜想吗?33猜想:两直角边a、b的平方和等于斜边c的平方.探索猜想 活动三1分割法添补法退出分割法添补法猜想猜想:两直角边a、b的平方
和等于斜边c的平方.退出论证猜想左图叫做玄图。是由四个相同的直角三角形拼成的。
如何证明我们的猜想呢?答案就在左图中小正方形退出退出演示论证猜想+=+=如何证明你的猜想呢?退出论证猜想正方形试一试:你能否根据左图论证你的猜想呢?想一想:你还有别的方法吗?退出 勾股定理(gou-gu theorem)勾股弦变式 在直角三角形中,两条直角边的平方和等于斜边的平方 即退出例题解析解答应用退出延伸题练习2 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长。(只考虑解法)ABCD添补分割法添补法43211234分割温馨提示:
利用勾股定理
两种方法:分割法和添补法退出温馨提示:可以考虑
构造直角三角形,过
B点作垂线BC,垂足为C点,则三角形ABC为
直角三角形,如图
所示,BC=6+2=8,
AC=8-2=6,退出练习3 (课本53页练习
第二题)求AB的距离.AB提高题演示退出本课小结谈谈你的收获小结3小结2小结1退出勾股史话★勾股定理迄今为止已有五千年历史。我国古代早在公元前1120年于著名的《周髀算经》中就已将勾股定理推广到一般情形了。
★ 《毕氏命题》搜集了370多种证明方法,包括大画家达芬奇和美国第二十任总统的证法
★美丽的勾股树
你一定见过多姿多彩的树木,可是你是否见过
美丽的勾股树呢?
