2022-2023学年京改版九年级数学下册24.3基本几何体的平面展开图课后练习(无答案)
文档属性
| 名称 | 2022-2023学年京改版九年级数学下册24.3基本几何体的平面展开图课后练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 17:29:31 | ||
图片预览



文档简介
24.3基本几何体的平面展开图课后练习
一、单选题(共 8 小题)
1、如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
2、如图,一只蚂蚁从长为,宽为,高为的长方体纸箱的A点沿纸箱表面爬到B点,那么他所爬行的最短路线的长为( )
A. B. C. D.
3、如图是一个正方体的平面展开图,若正方体相对面上的代数式的和都等于-1,则x的值是( )
A.-1 B.1
C.-2 D.2
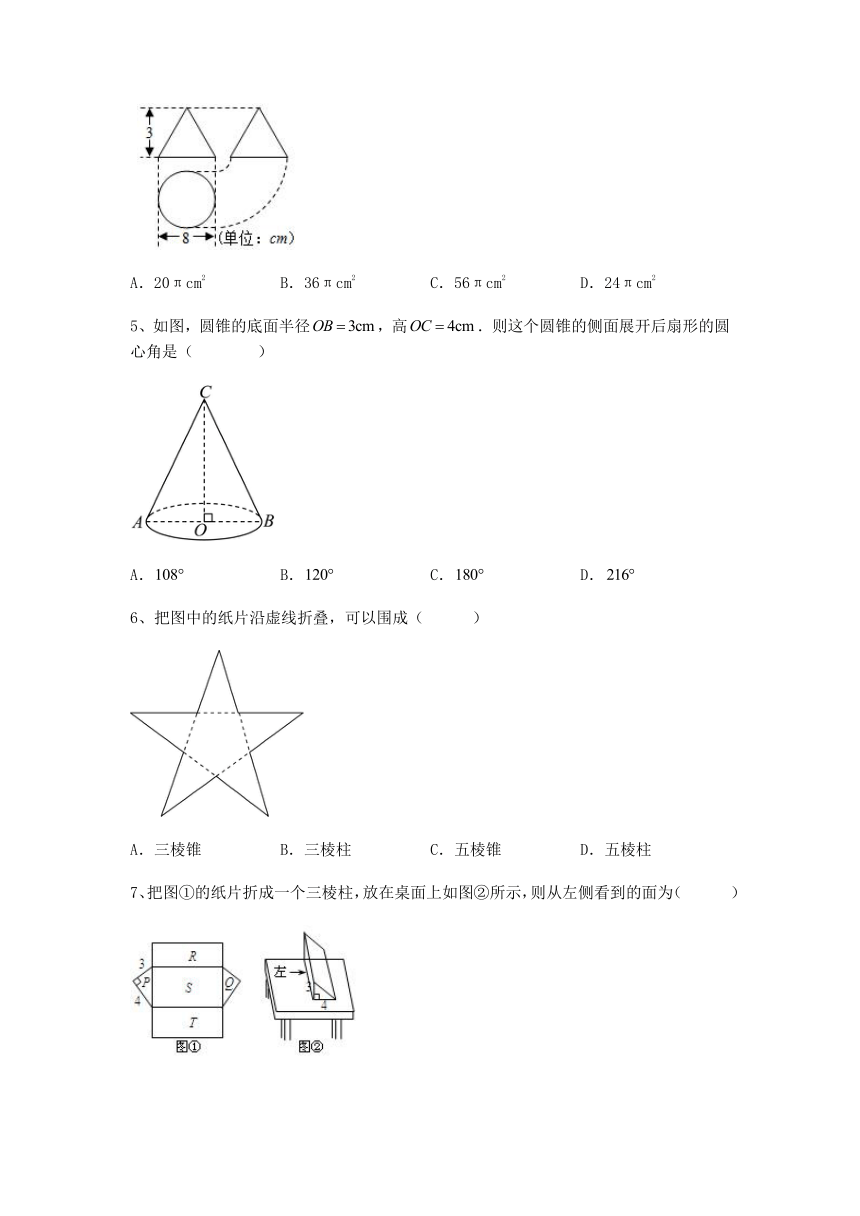
4、如图是某工件的三视图.则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
5、如图,圆锥的底面半径,高.则这个圆锥的侧面展开后扇形的圆心角是( )
A. B. C. D.
6、把图中的纸片沿虚线折叠,可以围成( )
A.三棱锥 B.三棱柱 C.五棱锥 D.五棱柱
7、把图①的纸片折成一个三棱柱,放在桌面上如图②所示,则从左侧看到的面为( )
A.Q B.R C.S D.T
8、一个小立方块六个面分别标有字母,,,,,,从三个不同方向看到的情形如下图所示,则,,对面的字母分别是( )
A.、、 B.、、 C.、、 D.、、
二、填空题(共 6 小题)
1、如图,圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是 _____°.
2、如图为由一些边长为1 cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.
3、如图①,是边长为的正方形纸板,裁掉阴影部分后折叠成如图②所示的长方体盒子,已知该长方体宽是高的2倍,则它的体积是_______________.
4、如图,在矩形中截取两个相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y和x,则因变量y与自变量x的函数关系式为y=_______.
5、学校花园边墙上有一宽为的矩形门,量得门框对角线长为,为美化校园,现准备打掉地面上方的部分墙体,使其变为以为直径的圆弧形门,则要打掉墙体(阴影部分)的面积是 __.
6、如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是______cm.(玻璃容器壁厚度忽略不计)
三、解答题(共 6 小题)
1、如图,若图中平面展开图折叠成正方体后,相对面上的两个数字互为相反数,求的值.
2、一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?
(2)若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?
3、综合实践
【问题情景】某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体形纸盒,如图1的四个图形中哪个图形经过折叠能围成无盖正方体形纸盒?
(2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的字是______.
(3)如图3,有一张边长为的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方形纸盒.
①请你在如图3中画出示意图,用实线表示剪切纸,虚线表示折痕.
②若四角各剪去了一个边长为的小正方形,用含的代数式表示这个纸盒的高为______,底面积为______;
③当四角剪去的小正方形的边长为时,求纸盒的容积.
4、如图,一个边长为10cm的无盖正方体可以展开成下面的平面图形.
(1)这个表面展开图的面积是 cm2;
(2)将一个无盖正方体展开成平面图形的过程中,需要剪开 条棱;
(3)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的图形(把需要的小正方形涂上阴影).
5、如图所示,是一个长方体纸盒平面展开图,已知纸盒中相对两个面上的数互为相反数.求a,b,c的值?
6、如图,是一个几何体的表面展开图,那么:
(1)该几何体与重合的点是________.
(2)若,,则该长方体的表面积和体积分别是多少?
一、单选题(共 8 小题)
1、如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
2、如图,一只蚂蚁从长为,宽为,高为的长方体纸箱的A点沿纸箱表面爬到B点,那么他所爬行的最短路线的长为( )
A. B. C. D.
3、如图是一个正方体的平面展开图,若正方体相对面上的代数式的和都等于-1,则x的值是( )
A.-1 B.1
C.-2 D.2
4、如图是某工件的三视图.则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
5、如图,圆锥的底面半径,高.则这个圆锥的侧面展开后扇形的圆心角是( )
A. B. C. D.
6、把图中的纸片沿虚线折叠,可以围成( )
A.三棱锥 B.三棱柱 C.五棱锥 D.五棱柱
7、把图①的纸片折成一个三棱柱,放在桌面上如图②所示,则从左侧看到的面为( )
A.Q B.R C.S D.T
8、一个小立方块六个面分别标有字母,,,,,,从三个不同方向看到的情形如下图所示,则,,对面的字母分别是( )
A.、、 B.、、 C.、、 D.、、
二、填空题(共 6 小题)
1、如图,圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是 _____°.
2、如图为由一些边长为1 cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.
3、如图①,是边长为的正方形纸板,裁掉阴影部分后折叠成如图②所示的长方体盒子,已知该长方体宽是高的2倍,则它的体积是_______________.
4、如图,在矩形中截取两个相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y和x,则因变量y与自变量x的函数关系式为y=_______.
5、学校花园边墙上有一宽为的矩形门,量得门框对角线长为,为美化校园,现准备打掉地面上方的部分墙体,使其变为以为直径的圆弧形门,则要打掉墙体(阴影部分)的面积是 __.
6、如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是______cm.(玻璃容器壁厚度忽略不计)
三、解答题(共 6 小题)
1、如图,若图中平面展开图折叠成正方体后,相对面上的两个数字互为相反数,求的值.
2、一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?
(2)若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?
3、综合实践
【问题情景】某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体形纸盒,如图1的四个图形中哪个图形经过折叠能围成无盖正方体形纸盒?
(2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的字是______.
(3)如图3,有一张边长为的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方形纸盒.
①请你在如图3中画出示意图,用实线表示剪切纸,虚线表示折痕.
②若四角各剪去了一个边长为的小正方形,用含的代数式表示这个纸盒的高为______,底面积为______;
③当四角剪去的小正方形的边长为时,求纸盒的容积.
4、如图,一个边长为10cm的无盖正方体可以展开成下面的平面图形.
(1)这个表面展开图的面积是 cm2;
(2)将一个无盖正方体展开成平面图形的过程中,需要剪开 条棱;
(3)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的图形(把需要的小正方形涂上阴影).
5、如图所示,是一个长方体纸盒平面展开图,已知纸盒中相对两个面上的数互为相反数.求a,b,c的值?
6、如图,是一个几何体的表面展开图,那么:
(1)该几何体与重合的点是________.
(2)若,,则该长方体的表面积和体积分别是多少?
