勾股定理
图片预览





文档简介
课件51张PPT。《拼图与勾股定理》 勾股定理有着悠久的历史,是人类最伟大的数学发现之一。但由于教材的编写遵循了简约性原则,在学习勾股定理知识的过程中,没能更深入地介绍它产生、发展的历史背景、多样的验证方法,以及在人类文化发展史上的贡献。
因此,在学生完成了《勾股定理》这章的学习之后,设置了《勾股定理的“无字证明”》的课题学习,它属于《数学课程标准》中所规定的“实践与综合应用”领域的内容,是对课本知识进一步的延伸和拓展,让学生更全面的认识勾股定理,了解拼图与定理证明之间的内在联系,通过经历综合应用知识解决问题的过程,领会其中的数学思想方法,以开拓学生视野,激发他们的创新意识和学习数学的兴趣。
《勾股定理证明方法汇总》 1.课前自主探究活动探究报告 请各个学习小组从网络或书籍上,尽可能多的寻找和了解验证勾股定理的方法。
2. 探 究 成 果 的
交 流 与 展 示
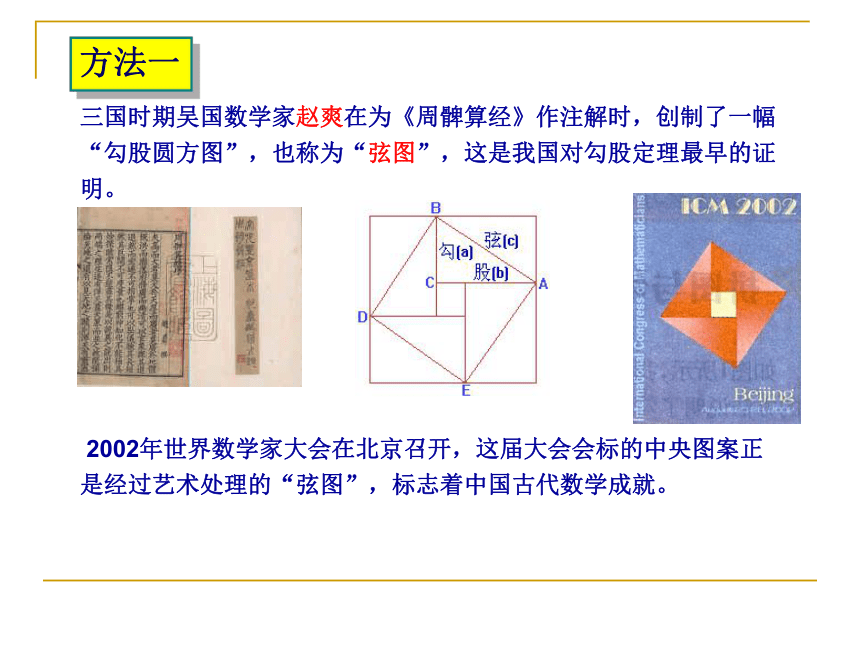
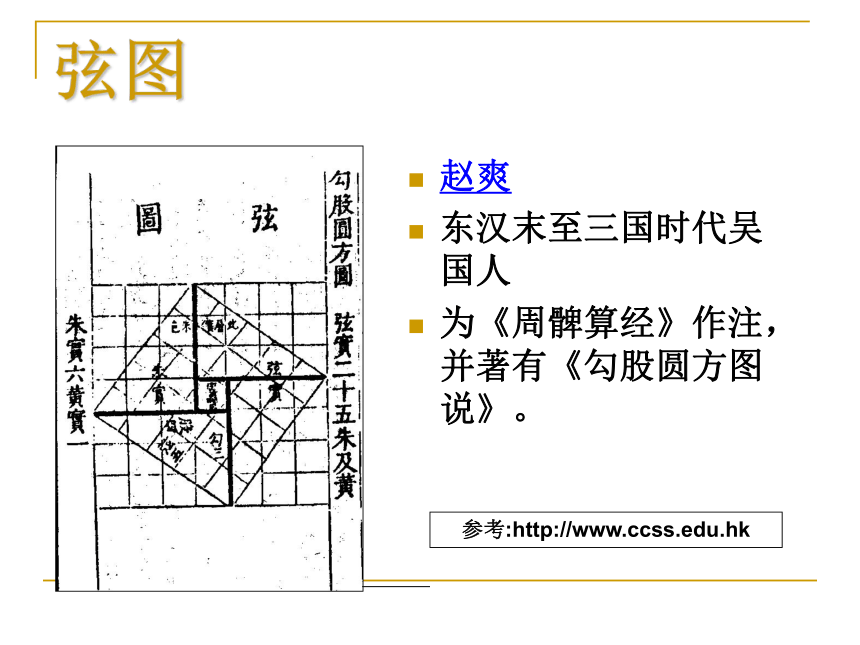
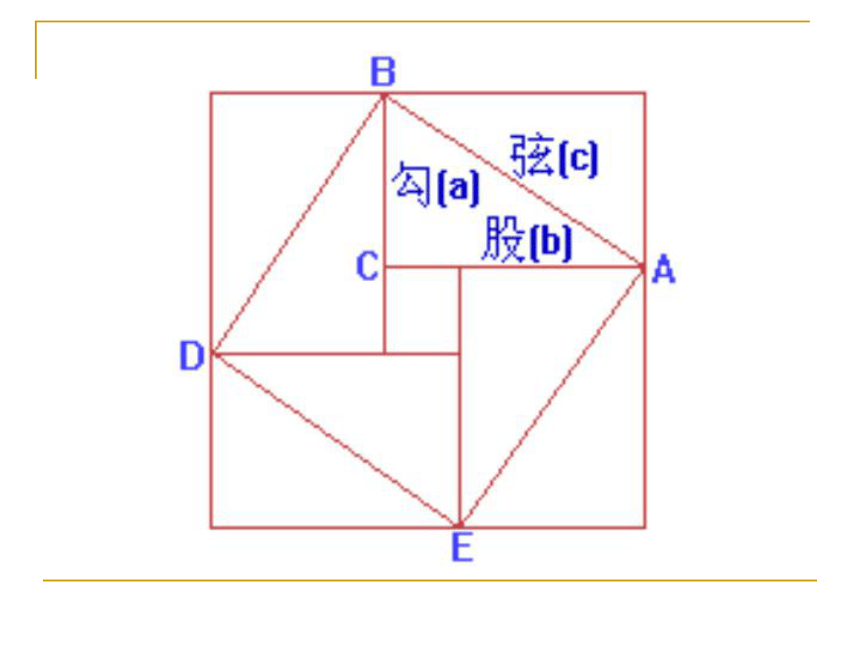
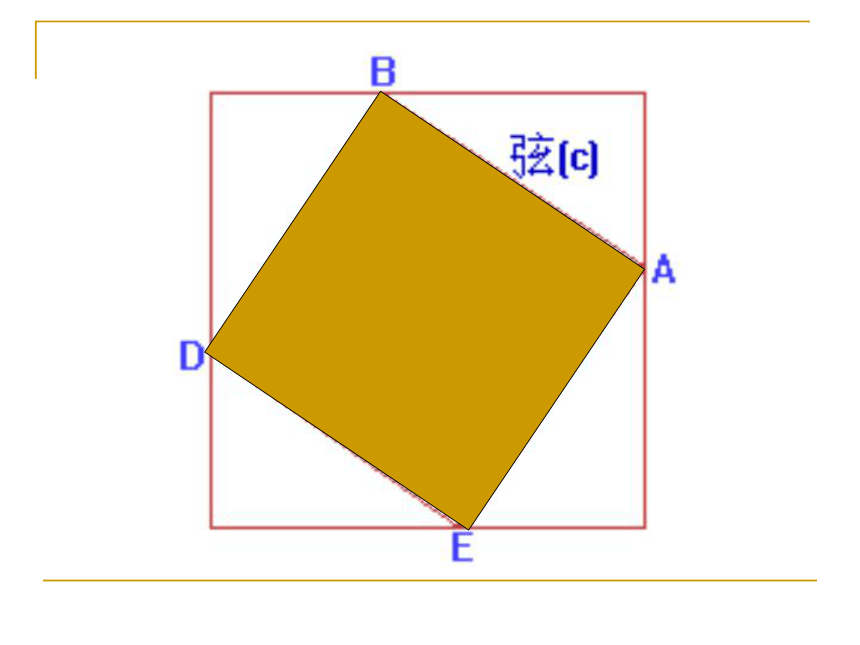
三国时期吴国数学家赵爽在为《周髀算经》作注解时,创制了一幅“勾股圆方图”,也称为“弦图”,这是我国对勾股定理最早的证明。 2002年世界数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。 方法一弦图赵爽
东汉末至三国时代吴国人
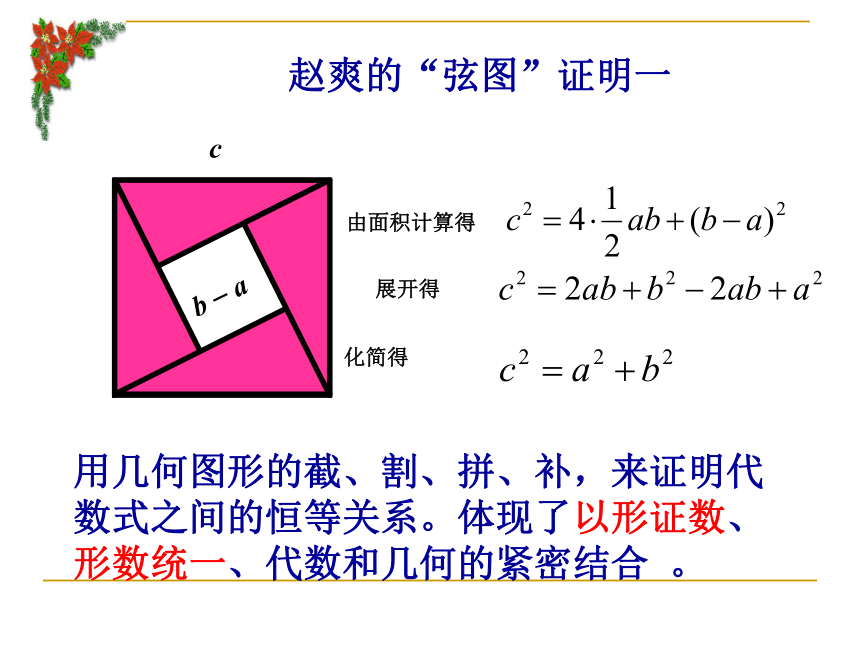
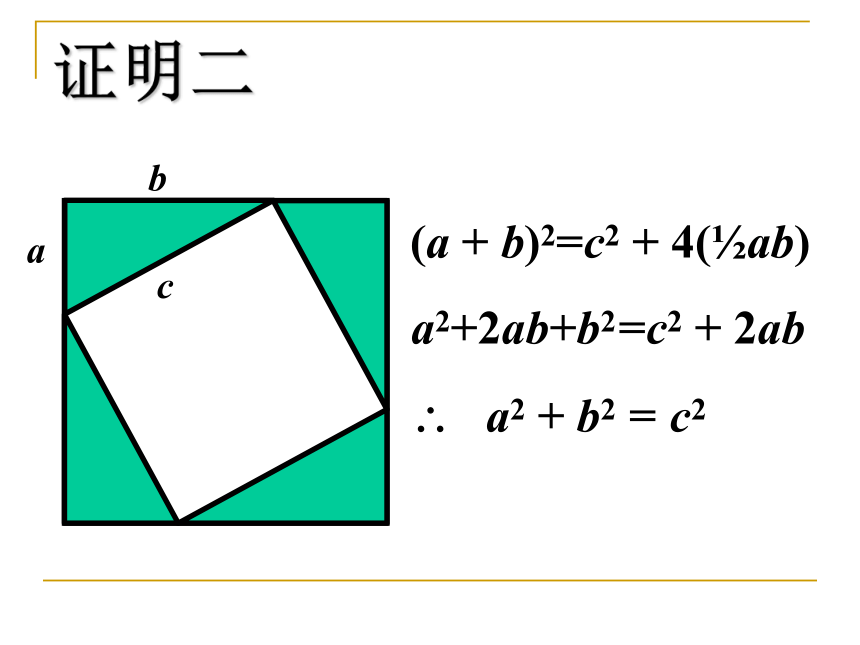
为《周髀算经》作注,并著有《勾股圆方图说》。参考:http://www.ccss.edu.hkcb ? a用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。赵爽的“弦图”证明一证明二ba(a + b)2= c2 + 4(?ab)
a2+2ab+b2 =c2 + 2ab
? a2 + b2 = c2c 美国总统的证明加菲(James A. Garfield,1831 ? 1881)1881 年成为美国第20 任总统.
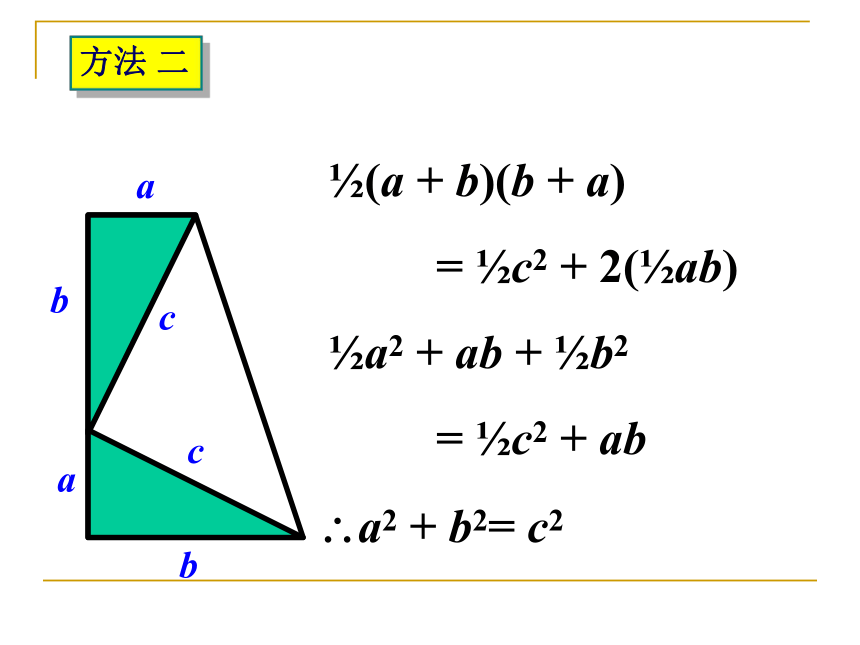
1876 年提出有关证明.参考:http://www.ccss.edu.hk方法 二 ?(a + b)(b + a)
= ?c2 + 2(?ab)
?a2 + ab + ?b2
= ?c2 + ab
?a2 + b2= c2aabbcc方法 二方法一与方法二的比较两个证明基本上相同! 方法一与方法二的比较两个证明基本上相同! 方法一与方法二的「缺点」两个证明都需要用到两个恒等式:
(a ? b)2 = a2 ? 2ab + b2 约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。 方法三a2b2证明c2? a2 + b2 = c2希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》给出一个公理化的证明。 1955年希腊为了纪念二千五百年前古希腊在勾股定理上的贡献,发行了一张邮票,图案是由三个棋盘排列而成。 方法四几何原本欧几里得(Euclid of Alexandria; 约 325 B.C. ? 约 265 B.C.)欧几里得的《几何原本》是用公理方法建立演绎数学体系的最早典范。
「证法四」就是取材自《几何原本》第一卷的第 47 命题。参考:http://www.ccss.edu.hk证明证明证明证明证明 画家的证法达· 芬奇(Leonardo Da Vinci 1452-1519 ).文艺复兴时期卓越的代表人物.
他不仅是一位天才的画家,并且是大数学家、科学家、力学家和工程师.
第一次在数学上使用加减(+、-)符号. 参考:http://yinhe2000.nease.net方法五abc方法五证明abc证明abcbca证明? a2 + b2 = c2下面据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a+b)的正方形ABCD,使中间留下边长c的一个正方形洞.画出正方形ABCD.移动三角形至图2所示的位置中,于是留下了边长分别为a与b的两个正方形洞.则图1和图2中的白色部分面积必定相等,所以c2=a2+b2图1图2abcabc5.尝试拼图,验证勾股定理拼图游戏青朱入出图拼图游戏c2拼图游戏拼图游戏拼图游戏拼图游戏a2b2? a2 + b2 = c2印度婆什迦羅的证明? c2 = b2 + a2注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 IIIIII注意:
面积 I : 面积II : 面积 III = a2 : b2 : c2 以上的证明方法都从几何图形的面积变化入手,运用了数形结合的思想方法,其中第一、二种类型还与拼图有着密切的关系。 4.勾股定理的文化价值(1) 勾股定理是联系数学中数与形的第一定理。(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应该认识它,因而勾股定理图被建议作为与“外星人”联系的信号。(3)勾股定理导致不可通约量的发现,引发第一次数学危机。(4)勾股定理公式是第一个不定方程,为不定方程的解题程序树立了一个范式。6.小结反思,课题拓展我最大的收获;我表现较好的方面;我学会了哪些知识;我还有哪些疑惑……学生反思:(1)写数学日记并发挥你的聪明才智,去探索勾股定理、去研究勾股定理,你又有什么新的发现?
(2)尝试用七巧板拼图,你能验证勾股定理吗?
课题拓展:评价表
因此,在学生完成了《勾股定理》这章的学习之后,设置了《勾股定理的“无字证明”》的课题学习,它属于《数学课程标准》中所规定的“实践与综合应用”领域的内容,是对课本知识进一步的延伸和拓展,让学生更全面的认识勾股定理,了解拼图与定理证明之间的内在联系,通过经历综合应用知识解决问题的过程,领会其中的数学思想方法,以开拓学生视野,激发他们的创新意识和学习数学的兴趣。
《勾股定理证明方法汇总》 1.课前自主探究活动探究报告 请各个学习小组从网络或书籍上,尽可能多的寻找和了解验证勾股定理的方法。
2. 探 究 成 果 的
交 流 与 展 示
三国时期吴国数学家赵爽在为《周髀算经》作注解时,创制了一幅“勾股圆方图”,也称为“弦图”,这是我国对勾股定理最早的证明。 2002年世界数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。 方法一弦图赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。参考:http://www.ccss.edu.hkcb ? a用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。赵爽的“弦图”证明一证明二ba(a + b)2= c2 + 4(?ab)
a2+2ab+b2 =c2 + 2ab
? a2 + b2 = c2c 美国总统的证明加菲(James A. Garfield,1831 ? 1881)1881 年成为美国第20 任总统.
1876 年提出有关证明.参考:http://www.ccss.edu.hk方法 二 ?(a + b)(b + a)
= ?c2 + 2(?ab)
?a2 + ab + ?b2
= ?c2 + ab
?a2 + b2= c2aabbcc方法 二方法一与方法二的比较两个证明基本上相同! 方法一与方法二的比较两个证明基本上相同! 方法一与方法二的「缺点」两个证明都需要用到两个恒等式:
(a ? b)2 = a2 ? 2ab + b2 约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。 方法三a2b2证明c2? a2 + b2 = c2希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》给出一个公理化的证明。 1955年希腊为了纪念二千五百年前古希腊在勾股定理上的贡献,发行了一张邮票,图案是由三个棋盘排列而成。 方法四几何原本欧几里得(Euclid of Alexandria; 约 325 B.C. ? 约 265 B.C.)欧几里得的《几何原本》是用公理方法建立演绎数学体系的最早典范。
「证法四」就是取材自《几何原本》第一卷的第 47 命题。参考:http://www.ccss.edu.hk证明证明证明证明证明 画家的证法达· 芬奇(Leonardo Da Vinci 1452-1519 ).文艺复兴时期卓越的代表人物.
他不仅是一位天才的画家,并且是大数学家、科学家、力学家和工程师.
第一次在数学上使用加减(+、-)符号. 参考:http://yinhe2000.nease.net方法五abc方法五证明abc证明abcbca证明? a2 + b2 = c2下面据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a+b)的正方形ABCD,使中间留下边长c的一个正方形洞.画出正方形ABCD.移动三角形至图2所示的位置中,于是留下了边长分别为a与b的两个正方形洞.则图1和图2中的白色部分面积必定相等,所以c2=a2+b2图1图2abcabc5.尝试拼图,验证勾股定理拼图游戏青朱入出图拼图游戏c2拼图游戏拼图游戏拼图游戏拼图游戏a2b2? a2 + b2 = c2印度婆什迦羅的证明? c2 = b2 + a2注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 IIIIII注意:
面积 I : 面积II : 面积 III = a2 : b2 : c2 以上的证明方法都从几何图形的面积变化入手,运用了数形结合的思想方法,其中第一、二种类型还与拼图有着密切的关系。 4.勾股定理的文化价值(1) 勾股定理是联系数学中数与形的第一定理。(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应该认识它,因而勾股定理图被建议作为与“外星人”联系的信号。(3)勾股定理导致不可通约量的发现,引发第一次数学危机。(4)勾股定理公式是第一个不定方程,为不定方程的解题程序树立了一个范式。6.小结反思,课题拓展我最大的收获;我表现较好的方面;我学会了哪些知识;我还有哪些疑惑……学生反思:(1)写数学日记并发挥你的聪明才智,去探索勾股定理、去研究勾股定理,你又有什么新的发现?
(2)尝试用七巧板拼图,你能验证勾股定理吗?
课题拓展:评价表
