沪科版七年级下学期期中考试数学试题三(含解析)
文档属性
| 名称 | 沪科版七年级下学期期中考试数学试题三(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-08 21:34:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
上海地区七年级数学下学期期中考试真题汇编
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.(2019春·上海浦东新·七年级上海市民办新竹园中学校考期中)如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则( )
A.当∠B为定值时,∠CDE为定值
B.当∠α为定值时,∠CDE为定值
C.当∠β为定值时,∠CDE为定值
D.当∠γ为定值时,∠CDE为定值
2.(2022春·上海闵行·七年级上海市七宝中学校考期中)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
3.(2018春·上海普陀·七年级统考期中)在、、、、、(每两个1之间增加一个3)这些数中,无理数的个数是( )
A.; B.; C.; D..
4.(2018春·上海浦东新·七年级统考期中)下列语句正确的是( )
A.无限小数是无理数 B.无理数是无限小数
C.实数分为正实数和负实数 D.两个无理数的和还是无理数
5.(2022春·上海·七年级统考期中)实数在数轴上的位置如图所示,下列各式正确的是( )
A. B. C. D.
6.(2019春·上海浦东新·七年级上海市民办新竹园中学校考期中)下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
7.(2022春·上海·七年级统考期中)下列各式正确的是( )
A. B. C. D.
8.(2019春·上海·七年级校考期中)如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A.120° B.108° C.126° D.114°
9.(2021春·上海·七年级上海市风华初级中学校考期中)下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
10.(2022春·上海·七年级期中)如图,A是直线l外一点,过点A作AB⊥l于点B,在直线l上取一点C,连结AC,使AC=2AB,P在线段BC上连结AP.若AB=3,则线段AP的长不可能是( )
A.3.5 B.4 C.5.5 D.6.5
二、填空题
11.(2019春·上海·七年级校考期中)在△ABC中,若∠A:∠B:∠C=1:1:2,则此三角形的形状为________.
12.(2021春·上海·七年级期中)比较大小:_____(填“>”、“<”或“=”).
13.(2019春·上海浦东新·七年级校考期中)如果一个数的平方根是和,则这个数为________.
14.(2022春·上海徐汇·七年级上海市徐汇中学校考期中)面积为2的正方形的边长是__________.
15.(2022春·上海闵行·七年级上海市闵行区莘松中学校考期中)化简:____.
16.(2022春·上海·七年级统考期中)写出一个比0大的无理数:___.
17.(2021春·上海·七年级校考期中)如图,点是上一点,,则图中与构成同旁内角的角有 ______ 个,这些角的度数和为 ______.
18.(2021春·上海·七年级校考期中)若,则______.
19.(2022春·上海松江·七年级校考期中)比较大小:______.
20.(2021春·上海宝山·七年级校考期中)如图,,则间的数量关系是_________.
21.(2022春·上海·七年级期中)如果正实数在数轴上对应的点到原点的距离是,那么______.
22.(2021春·上海·七年级校考期中)已知,是有理数,且,则______.
23.(2021春·上海·七年级校考期中)在三角形的三条高中,位于三角形外的可能条数是______条.
24.(2021春·上海·七年级校考期中)有一个如图的数值转换器,当输入的数是64时,输出的数是______.
25.(2022春·上海·七年级期中)求值:______.
26.(2021春·上海·七年级校考期中)有______个有效数字.
27.(2021春·上海·七年级校考期中)已知,,则的值是______.
28.(2022春·上海·七年级期中)实数m、n是连续整数,如果m<<n,那么m+n的值是_________________.
29.(2021春·上海·七年级校考期中)直角三角形的三条高的交点在___________________.
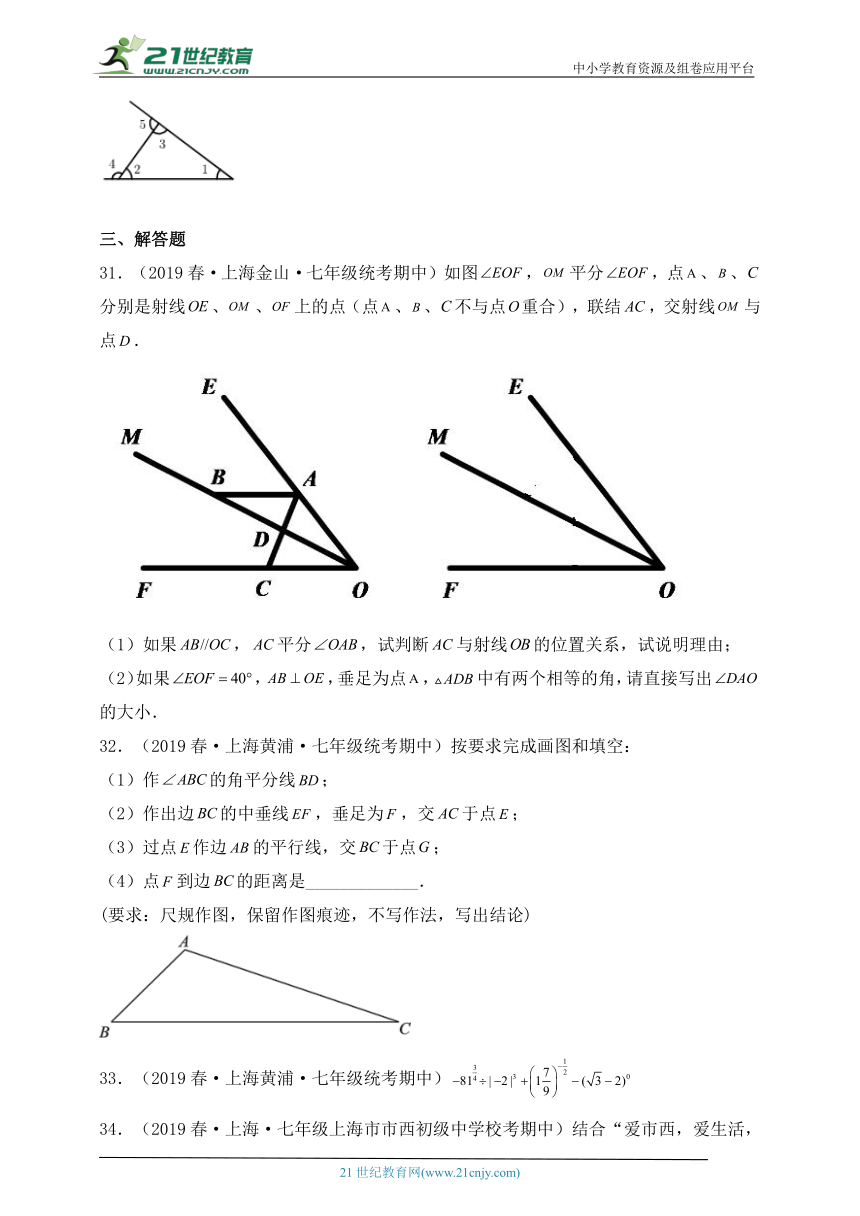
30.(2021春·上海·七年级校考期中)如图,同旁内角有_______________对.
三、解答题
31.(2019春·上海金山·七年级统考期中)如图,平分,点、、分别是射线、、上的点(点、、不与点重合),联结,交射线与点.
(1)如果,平分,试判断与射线的位置关系,试说明理由;
(2)如果,,垂足为点,中有两个相等的角,请直接写出的大小.
32.(2019春·上海黄浦·七年级统考期中)按要求完成画图和填空:
(1)作的角平分线;
(2)作出边的中垂线,垂足为,交于点;
(3)过点作边的平行线,交于点;
(4)点到边的距离是_____________.
(要求:尺规作图,保留作图痕迹,不写作法,写出结论)
33.(2019春·上海黄浦·七年级统考期中)
34.(2019春·上海·七年级上海市市西初级中学校考期中)结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯射线从开始顺时针旋转至便立即回转,灯射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是每秒2度,灯转动的速度是每秒1度.假定主道路是平行的,即,且.
(1)填空:______;
(2)若灯射线先转动60秒,灯射线才开始转动,在灯射线到达之前,灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯射线到达之前,若射出的光束交于点,过作交于点,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
35.(2019春·上海·七年级上海市市西初级中学校考期中).
36.(2019春·上海·七年级上海市市西初级中学校考期中)细心观察图,认真分析各式,然后解答问题:
;
;
;
(1)请用含(为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于的长度;
(4)若表示三角形面积,,,,计算出的值.
37.(2020春·上海·七年级校考期中)已知∠CDA=∠CBA,DE 平分∠CDA,BF 平分∠CBA.且∠1=∠2,请说明 DE//FB 的理由.
解:因为 DE 平分∠CDA( )
所以( )
因为 BF 平分∠CBA( )
所以( )
( 完 成 以 下 说 理 过 程 )
38.(2020春·上海·七年级校考期中)如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.
解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
39.(2020春·上海·七年级校考期中)计算:
40.(2019春·上海普陀·七年级统考期中)按照下列要求画图并填空:
如图,点是的边上的一点,
(1)过点作的垂线,交于点;
(2)在(1)的基础上作的边上的高,垂足为;
(3)线段___________的长度是点到直线的距离;
(4)线段这三条线段大小关系是___________(用“<”号连接).
41.(2019春·上海普陀·七年级统考期中)计算:.
42.(2019春·上海浦东新·七年级校联考期中)已知与互为相反数,求的值.
43.(2019春·上海松江·七年级校考期中)如图,已知是线段的中点,,且,试说明的理由.
44.(2022春·上海·七年级期中)利用分数指数幂的运算性质进行计算:
45.(2019春·上海金山·七年级统考期中)如图,已知线段.
(1)画图:①在的上方画,使,且,联结;
②过点作(为垂足);
③取的中点,过点作交于点.
(2)填空:
①线段长 是点到点的距离;
②线段长 是点到直线的距离;
③线段长 是平行线和间的距离.
参考答案:
1.B
【详解】试题分析:本题主要考查等腰三角形的性质和外角的性质,掌握等边对等角和三角形的外角等于不相邻两内角的和是解题的关键.根据等边对等角,可找到角之间的关系,再利用外角的性质可找到∠CDE和∠1之间的关系,从而得到答案.
解:
A∵AB=AC,
∴∠B=∠C,
又∠ADC=∠α+∠B,
∴∠ADE=∠ADC-∠CDE=∠α+∠B-∠CDE,
∵AD=AE,
∴∠ADE=∠γ=∠CDE+∠C=∠CDE+∠B,
∴∠1+∠B-∠CDE=∠CDE+∠B,
∴∠1=2∠CDE,
∴当∠α为定值时,∠CDE为定值,
故选B.
考点:等腰三角形的性质.
2.A
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
【详解】∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
【点睛】本题考查了角平分线的定义和三角形内角和定理,解决问题的关键是三角形外角性质以及角平分线的定义的运用.
3.D
【详解】分析: 根据无理数的三种形式求解.
详解:、、、(每两个1之间增加一个3)是无理数,共4个.
故选D.
点睛:本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
4.B
【详解】解:A.无限不循环小数是无理数,故A错误;
B.无理数是无限小数,正确;
C.实数分为正实数、负实数和0,故C错误;
D.互为相反数的两个无理数的和是0,不是无理数,故D错误.
故选B.
5.D
【分析】根据数轴上的数,右边的总比左边的大即可解答.
【详解】观察数轴可得:a<0<b,
∴选项A、B、C错误,选项D正确.
故选D.
【点睛】本题考查了数轴和有理数数的应用,解题的关键是掌握数轴上的数,右边的总比左边的大这一性质.
6.A
【分析】结合已知条件和全等三角形的判定方法,对所给的三个命题依次判定,即可解答..
【详解】①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选A.
【点睛】本题主要考查全等三角形的判定方法,要求学生能对常用的判定方法熟练掌握并能进行灵活运用.解决命题②时,可以用“倍长中线法”.
7.C
【分析】根据有数的乘方、立方根和平方根的知识即可判断.
【详解】A、,故选项A错误;
B、,故选项B错误;
C、,,故选项C正确;
D、=3,故选项D错误.
故选C.
【点睛】此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.
8.D
【分析】如图,设∠B′FE=x,根据折叠的性质得∠BFE=∠B′FE=x,∠AEF=∠A′EF,则∠BFC=x-18°,再由第2次折叠得到∠C′FB=∠BFC=x-18°,于是利用平角定义可计算出x=66°,接着根据平行线的性质得∠A′EF=180°-∠B′FE=114°,所以∠AEF=114°.
【详解】如图,设∠B′FE=x,
∵纸条沿EF折叠,
∴∠BFE=∠B′FE=x,∠AEF=∠A′EF,
∴∠BFC=∠BFE ∠CFE=x 18°,
∵纸条沿BF折叠,
∴∠C′FB=∠BFC=x 18°,
而∠B′FE+∠BFE+∠C′FB=180°,
∴x+x+x 18°=180°,解得x=66°,
∵A′D′∥B′C′,
∴∠A′EF=180° ∠B′FE=180° 66°=114°,
∴∠AEF=114°.
故答案选:D.
【点睛】本题考查了翻折变换(折叠问题)与平行线的性质,解题的关键是熟练的掌握翻折变换(折叠问题)与平行线的性质.
9.B
【分析】根据平行线的性质逐项判断即可.
【详解】A、∵AB//CD,
∴∠1+∠2=180°.故本选项不符合题意;
B、如图,∵AB//CD,
∴∠1=∠3.
∵∠2=∠3,
∴∠1=∠2.故本选项正确.
C、∵AB//CD,
∴∠BAD=∠CDA,不能得到∠1=∠2.故本选项不符合题意;
D、当梯形ABDC是等腰梯形时才有,∠1=∠2.故本选项不符合题意.
故选:B.
【点睛】本题考查平行线的性质,熟练掌握平行线的性质是解答的关键.
10.D
【分析】直接利用垂线段最短以及结合已知得出AP的取值范围进而得出答案.
【详解】∵过点A作AB⊥l于点B,AC=2AB,P在线段BC上连结AP,AB=3,∴AC=6,∴3≤AP≤6,故AP不可能是6.5.
故选D.
【点睛】本题考查了垂线段最短,正确得出AP的取值范围是解题的关键.
11.等腰直角三角形
【分析】设∠A=x,根据题意和三角形的内角和定理可得关于x的方程,解方程即可求出x,进而可得答案.
【详解】解:因为在△ABC中,∠A:∠B:∠C=1:1:2,
所以设∠A=x,则∠B=x,∠C=2x,
因为∠A+∠B+∠C=180°,
所以x+x+2x=180°,解得:x=45°,
所以∠A=45°,∠B=45°,∠C=90°,
所以这个三角形的形状为等腰直角三角形.
故答案为:等腰直角三角形.
【点睛】本题考查了三角形的内角和定理和特殊三角形的判定,属于基础题型,熟练掌握基本知识是解题的关键.
12.<
【分析】先把根号外的因式移入根号内,再比较大小即可.
【详解】∵=,=,<,
∴<,
故答案为:<
【点睛】本题考查了比较二次根式的大小,能选择适当的方法比较两个实数的大小是解此题的关键.
13.49
【分析】根据正数有两个平方根,它们互为相反数,先求出a的值,再求出这个数的平方.
【详解】解:因为一个非负数的平方根互为相反数,
所以a+3+2a-15=0
解得a=4
所以a+3=7
72=49.
即这个数是49.
故答案为49.
【点睛】本题考查了平方根的意义,根据正数的平方根互为相反数列出方程,是解决本题的关键.
14.
【分析】设正方形的边长为x,根据题意得,求解即可.
【详解】解:设正方形的边长为x,
由题意得,
∴x=(负值舍去),
故答案为:.
【点睛】此题考查平方根的实际应用,正确求一个数的平方根是解题的关键.
15.
【分析】根据二次根式乘除法运算法则进行计算即可得到答案.
【详解】解:
=
=.
故答案为:.
【点睛】此题主要考查了二次根式的乘除运算,掌握运算法则是解答此题的关键.
16.(答案不唯一)
【分析】本题需先根据已知条件,写出一个正数并且是无理数即可求出答案.
【详解】比0大的无理数有,等,
故答案为:(答案不唯一).
【点睛】本题主要考查无理数,用到的知识点是无理数的定义和实数的比较大小,在解题时根据正无理数的定义写出结果是解题关键.
17. 4; 230.
【分析】根据同旁内角的角的定义即可写出的所有同旁内角是,,,;根据三角形的内角和定理得,,据此求出,,,的和即可.
【详解】解:由图像可知图中与构成同旁内角的角有,,,,共计4个,
由三角形的内角和定理可得:
,
,
∴
故答案是:4,230.
【点睛】本题主要考查了同旁内角的角,三角形的内角和定理等知识点,熟悉相关知识点是解题的关键.
18.16
【分析】等式两边同时平方即可求出答案.
【详解】解:∵
∴
故答案为:16.
【点睛】此题主要考查了算术平方根,注意:一个非负数的算术平方根是非负数.
19.>
【分析】任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.
【详解】解:∵,
∴,
∴,
故答案为:>.
【点睛】本题主要考查了实数大小的比较,在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.
20.∠2+∠4=∠1+∠3
【分析】分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
【详解】解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
【点睛】本题考查的是平行线的性质,即两直线平行,内错角相等.
21.
【分析】根据数轴的特点即可求解.
【详解】∵实数在数轴上对应的点到原点的距离是,
∴a=±
∵a为正
∴
故答案为:.
【点睛】此题主要考查实数与数轴,解题的关键是熟知数轴的特点.
22.
【分析】将等式的左边展开,根据,是有理数求得a、b值,即可求解.
【详解】解:∵,且,是有理数,
∴a=﹣1,b=1,
∴ab=(﹣1)×1=﹣1,
故答案为:﹣1.
【点睛】本题考查实数的运算、代数式的求值,掌握实数的运算法则是解答的关键.
23.0或2
【分析】当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内;当三角形为直角三角形和锐角三角形时没有高在三角形外.
【详解】解:∵当三角形为直角三角形和锐角三角形时,没有高在三角形外;而当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内.
∴在三角形的三条高中,位于三角形外的可能条数是0或2条
故答案为0或2.
【点睛】此题主要考查了三角形的高的位置,不同形状的三角形,它的高的情况不同,要求学生必须熟练掌握.
24.
【分析】根据实数的性质及算术平方根的定义即可求解.
【详解】输入64时,取算术平方根为=8,为有理数;
再去算术平方根为=,为无理数,故输出
故答案为:.
【点睛】此题主要考查程序的计算,解题的关键是熟知实数的性质及算术平方根的定义.
25.
【分析】先求出根式里的数,再根据实数的性质进行化简.
【详解】
故答案为:.
【点睛】此题主要考查实数的运算,解题的关键是熟知实数的性质.
26.3
【分析】根据有效数字的定义即可求解.
【详解】的有效数字为6、1、0
故答案为:3.
【点睛】此题主要考查有效数字的个数,解题的关键是熟知有效数字的定义.
27.100
【分析】先计算,即可得到的值.
【详解】∵,
∴
∴=
故答案为:100.
【点睛】此题主要考查二次根式的运算,解题的关键是熟知其运算法则.
28.9
【分析】根据题意可得,即可得 , ,即可求解.
【详解】∵ ,
∴,
∴ , ,
∴ .
故答案为:
【点睛】本题主要考查了估算无理数的大小,解题的关键是正确估算出该无理数在哪两个连续的整数之间.
29.直角顶点
【分析】根据三角形高的概念解答即可.
【详解】解:∵直角三角形有两条高与直角边重合,
∴它们的交点是直角顶点.
故答案为:直角顶点.
【点睛】本题考查的是三角形的高的概念,注意:锐角三角形的三条高在三角形的内部,相交于三角形内一点;直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
30.4
【分析】根据同旁内角定义:两条直线被第三条直线所截,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进行分析即可.
【详解】解:∠1和∠2,∠1和∠3,∠2和∠3,∠4和∠5是同旁内角,共4对,
故答案为:4.
【点睛】此题主要考查了同旁内角的定义,关键是掌握同旁内角的边构成“U”形.
31.(1)与射线垂直,理由见解析;(2)的大小为或或.
【分析】(1)先根据平行线的性质、角平分线的定义得出,再根据角平分线的定义得出,最后根据三角形的外角性质、领补角的定义即可得出结论;
(2)先根据角平分线的定义、直角三角形的性质求出和的度数,再根据“中有两个相等的角”分三种情况,然后分别根据三角形的外角性质、角的和差求解即可得.
【详解】(1)与射线垂直,理由如下:
如图1,
平分,平分
,
由三角形的外角性质得:
又
即与射线垂直;
(2)平分,
如图2,由题意,分以下三种情况:
①当时
(三角形的外角性质)
②当时
③当时
则
解得
综上,的大小为或或.
【点睛】本题考查了平行线的性质、垂直的定义、三角形的外角性质等知识点,较难的是题(2),依据题意,正确分三种情况讨论是解题关键.
32.(1)见解析;(2)见解析;(3)见解析;(4)0
【分析】(1)根据角平分线的作法,即可得到的角平分线BD;
(2)根据垂直平分线的作法,即可得到边的中垂线;
(3)根据同位角相等,两直线平行,作即可得到;
(4)由点F在边BC上,可得点F到边BC的距离为0.
【详解】解:(1)如图所示,射线即为所求;
(2)如图所示,直线即为所求;
(3)如图所示,直线即为所求;
(4)∵点F在边BC上,
∴点到边的距离为0,
故答案为:0.
【点睛】本题主要考查了尺规作图-基本作图和点到直线的距离,熟练掌握角平分线的作法、垂直平分线的作法和作一个角等于已知角的作法是解题的关键.
33.
【分析】先计算分数指数幂、绝对值和零指数幂,再进一步计算即可求得结果.
【详解】原式
【点睛】本题主要考查实数的运算,解题的关键是熟练掌握分数指数幂、绝对值和零指数幂.
34.(1)120;(2)灯转动100秒,两灯的光束互相平行;(3)在转动过程中,和关系不会变化,且有,理由见解析.
【分析】(1)先根据角的倍差求出的度数,再根据平行线的性质即可得;
(2)设A灯转动时间为t秒,先求出两个临界位置:灯射线从开始顺时针旋转至、灯射线从开始顺时针旋转至,再分三种情况,分别利用平行线的性质列出等式求解即可得;
(3)先根据角的和差求出,再根据三角形的内角和定理可得,然后根据角的和差可得,由此即可得.
【详解】(1)∵,
∴
(两直线平行,内错角相等)
故答案为:120;
(2)设A灯转动时间为t秒
灯射线从开始顺时针旋转至所需时间为(秒),灯射线从开始顺时针旋转至所需时间为(秒)
灯射线从开始顺时针旋转至所需时间为(秒)
则t的取值范围为,即
由题意,分以下三种情况:
①当时,如图1所示
∵
∴
∵
∴
∴
∴
解得
此时,
即两灯的光束重合,不符题意,舍去
②当时,如图2所示,此时灯A射线未从AN回转
∵
∴
∵
∴
∴
∴
解得(不符题设,舍去)
③当时,如图2所示,此时灯A射线旋转至AN,并已开始回转
∵
∴
∵
∴
∴
∴
解得,符合题设
综上,灯转动100秒,两灯的光束互相平行;
(3)和关系不会变化,且有,理由如下:
设灯A射线转动时间为t秒
∵
∴
又∵
∴
∴
∴,即
故在转动过程中,和关系不会变化,且有.
【点睛】本题考查了平行线的性质、角的和差倍分、三角形的内角和定理等知识点,较难的是题(2),依据题意,找出两个临界位置,进而分三种情况讨论是解题关键.
35.
【分析】根据负指数幂、平方根与立方根、二次根式的加减法、除法运算计算即可.
【详解】原式
.
【点睛】本题考查了负指数幂、平方根与立方根、二次根式的加减法、除法运算,熟记各运算法则是解题关键.
36.(1);(2)直角边的平方和等于斜边的平方;(3)见解析;(4).
【分析】(1)观察已知各式,归纳总结规律即可得;
(2)根据等式和图形即可得;
(3)先作的垂线,再在垂线上截取,连接,可得,同理可作出点,连接即为所求;
(4)先分别求出的值,再归纳总结出一般规律得出的值,从而可得的值,然后代入求和即可.
【详解】(1)观察已知各式可得,各式的变化规律为
故答案为:;
(2)结合等式和图形可得,直角三角形两条直角边与斜边的关系为:直角边的平方和等于斜边的平方
故答案为:直角边的平方和等于斜边的平方;
(3)先作的垂线,再在垂线上截取,连接,即可得,同理可作点,连接,则即为所求,如图所示:
(4)
归纳类推得:
当时,
则
.
【点睛】本题考查了算术平方根、勾股定理等知识点,读懂题意,正确归纳类推出一般规律是解题关键.
37.见解析
【分析】根据角平分线定义和已知求出∠1=∠3,推出∠2=∠3,根据平行线的判定推出即可.
【详解】∵DE平分∠CDA(已知),
∴(角平分线的定义),
∵BF平分∠CBA(已知),
∴(角平分线的定义),
∵∠CDA=∠CBA(已知),
∴∠1=∠3(等量代换),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴DE//FB(同位角相等,两直线平行).
【点睛】本题考查了平行线的判定和角平分线定义的应用,注意:同位角相等,两直线平行.
38.已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等
【分析】先证得AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
【详解】∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD(等量代换),
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等.
【点睛】本题考查了平行线的性质和判定,垂直定义,补角定义的应用,能综合运用定理进行推理是解此题的关键.
39.6
【分析】逆用积的乘方,再运用幂的乘方运算法则计算即可.
【详解】
.
【点睛】本题考查了逆用积的乘方,运用幂的乘方运算法则计算是解题的关键.
40.(1)作图见解析;(2)作图见解析;(3);(4)
【分析】(1)过点P作∠OPC=90°,交OA于C即可;
(2)过点P作∠PHO=90°交OA于H即可;
(3)根据点到直线的距离定义,可得线段PH的长度是点到直线的距离.
(4)垂线段最短的性质可得,线段PC、PH、OC这三条线段大小关系是PH【详解】(1)过点P作∠OPC=90°,交OA于C点,如图所示;
(2)过点P作∠PHO=90°交OA于H点,如图所示;
(3)根据点到直线的距离定义,
可得线段PH的长度是点到直线的距离.
故答案为:PH
(4)根据垂线段最短性质可得
在Rt△PHC中,PC>PH
在Rt△OHP中,OC>PC
∴线段PC、PH、OC这三条线段大小关系是PH故答案为:PH【点睛】本题考查了基本作图:过一点作已知直线的垂线,本题还查考了点到直线的距离的定义及垂线段最短的性质.
41.
【分析】根据二次根式的运算法则,先算括号里的,再算乘除,最后算加减,即可求解.
【详解】解:原式
故答案为:
【点睛】本题考查了二次根式的混合运算,在运算中要掌握好运算的顺序及运算规律.
42.3
【分析】根据相反数的性质化简得,再代入原式求解即可.
【详解】解:与互为相反数,
与互为相反数,即
化简得
即
原式
【点睛】本题考查了分式的运算问题,掌握相反数的性质是解题的关键.
43.见解析
【分析】根据中点定义求出AC=CB,两直线平行,同位角相等,求出∠ACD=∠B,然后证明△ACD和△CBE全等,再利用全等三角形的对应角相等进行解答.
【详解】解:∵C是AB的中点,
∴AC=CB(线段中点的定义).)
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
∴∠D=∠E(全等三角形的对应角相等).
【点睛】本题主要考查了全等三角形的判定与全等三角形的性质,确定用SAS定理进行证明是关键.
44.4
【分析】首先将每个根式化为以2为底数的幂,然后根据同底数幂的除法与乘法运算法则求解即可求得答案.
【详解】解:原式
【点睛】此题考查了分数指数幂的知识.此题难度适中,解题的关键是掌握分数指数幂的定义,同底数幂的除法与乘法运算法则.
45.(1)画图见解析;(2)①,②,③
【分析】(1)根据角、线段、垂线、平行线的画法即可得;
(2)①根据点到点的距离定义即可得;
②根据点到直线的距离定义即可得;
③根据平行线间的距离即可得.
【详解】(1)根据角、线段、垂线、平行线的画法,作图结果如下:
(2)①线段长AC是点到点的距离
②线段长BD是点到直线的距离
③
则线段长ND是平行线和间的距离
故答案为:①,②,③.
【点睛】本题考查了角、线段、垂线、平行线的画法,理解题意,正确画出图形是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
上海地区七年级数学下学期期中考试真题汇编
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.(2019春·上海浦东新·七年级上海市民办新竹园中学校考期中)如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则( )
A.当∠B为定值时,∠CDE为定值
B.当∠α为定值时,∠CDE为定值
C.当∠β为定值时,∠CDE为定值
D.当∠γ为定值时,∠CDE为定值
2.(2022春·上海闵行·七年级上海市七宝中学校考期中)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
3.(2018春·上海普陀·七年级统考期中)在、、、、、(每两个1之间增加一个3)这些数中,无理数的个数是( )
A.; B.; C.; D..
4.(2018春·上海浦东新·七年级统考期中)下列语句正确的是( )
A.无限小数是无理数 B.无理数是无限小数
C.实数分为正实数和负实数 D.两个无理数的和还是无理数
5.(2022春·上海·七年级统考期中)实数在数轴上的位置如图所示,下列各式正确的是( )
A. B. C. D.
6.(2019春·上海浦东新·七年级上海市民办新竹园中学校考期中)下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
7.(2022春·上海·七年级统考期中)下列各式正确的是( )
A. B. C. D.
8.(2019春·上海·七年级校考期中)如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A.120° B.108° C.126° D.114°
9.(2021春·上海·七年级上海市风华初级中学校考期中)下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
10.(2022春·上海·七年级期中)如图,A是直线l外一点,过点A作AB⊥l于点B,在直线l上取一点C,连结AC,使AC=2AB,P在线段BC上连结AP.若AB=3,则线段AP的长不可能是( )
A.3.5 B.4 C.5.5 D.6.5
二、填空题
11.(2019春·上海·七年级校考期中)在△ABC中,若∠A:∠B:∠C=1:1:2,则此三角形的形状为________.
12.(2021春·上海·七年级期中)比较大小:_____(填“>”、“<”或“=”).
13.(2019春·上海浦东新·七年级校考期中)如果一个数的平方根是和,则这个数为________.
14.(2022春·上海徐汇·七年级上海市徐汇中学校考期中)面积为2的正方形的边长是__________.
15.(2022春·上海闵行·七年级上海市闵行区莘松中学校考期中)化简:____.
16.(2022春·上海·七年级统考期中)写出一个比0大的无理数:___.
17.(2021春·上海·七年级校考期中)如图,点是上一点,,则图中与构成同旁内角的角有 ______ 个,这些角的度数和为 ______.
18.(2021春·上海·七年级校考期中)若,则______.
19.(2022春·上海松江·七年级校考期中)比较大小:______.
20.(2021春·上海宝山·七年级校考期中)如图,,则间的数量关系是_________.
21.(2022春·上海·七年级期中)如果正实数在数轴上对应的点到原点的距离是,那么______.
22.(2021春·上海·七年级校考期中)已知,是有理数,且,则______.
23.(2021春·上海·七年级校考期中)在三角形的三条高中,位于三角形外的可能条数是______条.
24.(2021春·上海·七年级校考期中)有一个如图的数值转换器,当输入的数是64时,输出的数是______.
25.(2022春·上海·七年级期中)求值:______.
26.(2021春·上海·七年级校考期中)有______个有效数字.
27.(2021春·上海·七年级校考期中)已知,,则的值是______.
28.(2022春·上海·七年级期中)实数m、n是连续整数,如果m<<n,那么m+n的值是_________________.
29.(2021春·上海·七年级校考期中)直角三角形的三条高的交点在___________________.
30.(2021春·上海·七年级校考期中)如图,同旁内角有_______________对.
三、解答题
31.(2019春·上海金山·七年级统考期中)如图,平分,点、、分别是射线、、上的点(点、、不与点重合),联结,交射线与点.
(1)如果,平分,试判断与射线的位置关系,试说明理由;
(2)如果,,垂足为点,中有两个相等的角,请直接写出的大小.
32.(2019春·上海黄浦·七年级统考期中)按要求完成画图和填空:
(1)作的角平分线;
(2)作出边的中垂线,垂足为,交于点;
(3)过点作边的平行线,交于点;
(4)点到边的距离是_____________.
(要求:尺规作图,保留作图痕迹,不写作法,写出结论)
33.(2019春·上海黄浦·七年级统考期中)
34.(2019春·上海·七年级上海市市西初级中学校考期中)结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯射线从开始顺时针旋转至便立即回转,灯射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是每秒2度,灯转动的速度是每秒1度.假定主道路是平行的,即,且.
(1)填空:______;
(2)若灯射线先转动60秒,灯射线才开始转动,在灯射线到达之前,灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯射线到达之前,若射出的光束交于点,过作交于点,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
35.(2019春·上海·七年级上海市市西初级中学校考期中).
36.(2019春·上海·七年级上海市市西初级中学校考期中)细心观察图,认真分析各式,然后解答问题:
;
;
;
(1)请用含(为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于的长度;
(4)若表示三角形面积,,,,计算出的值.
37.(2020春·上海·七年级校考期中)已知∠CDA=∠CBA,DE 平分∠CDA,BF 平分∠CBA.且∠1=∠2,请说明 DE//FB 的理由.
解:因为 DE 平分∠CDA( )
所以( )
因为 BF 平分∠CBA( )
所以( )
( 完 成 以 下 说 理 过 程 )
38.(2020春·上海·七年级校考期中)如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.
解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
39.(2020春·上海·七年级校考期中)计算:
40.(2019春·上海普陀·七年级统考期中)按照下列要求画图并填空:
如图,点是的边上的一点,
(1)过点作的垂线,交于点;
(2)在(1)的基础上作的边上的高,垂足为;
(3)线段___________的长度是点到直线的距离;
(4)线段这三条线段大小关系是___________(用“<”号连接).
41.(2019春·上海普陀·七年级统考期中)计算:.
42.(2019春·上海浦东新·七年级校联考期中)已知与互为相反数,求的值.
43.(2019春·上海松江·七年级校考期中)如图,已知是线段的中点,,且,试说明的理由.
44.(2022春·上海·七年级期中)利用分数指数幂的运算性质进行计算:
45.(2019春·上海金山·七年级统考期中)如图,已知线段.
(1)画图:①在的上方画,使,且,联结;
②过点作(为垂足);
③取的中点,过点作交于点.
(2)填空:
①线段长 是点到点的距离;
②线段长 是点到直线的距离;
③线段长 是平行线和间的距离.
参考答案:
1.B
【详解】试题分析:本题主要考查等腰三角形的性质和外角的性质,掌握等边对等角和三角形的外角等于不相邻两内角的和是解题的关键.根据等边对等角,可找到角之间的关系,再利用外角的性质可找到∠CDE和∠1之间的关系,从而得到答案.
解:
A∵AB=AC,
∴∠B=∠C,
又∠ADC=∠α+∠B,
∴∠ADE=∠ADC-∠CDE=∠α+∠B-∠CDE,
∵AD=AE,
∴∠ADE=∠γ=∠CDE+∠C=∠CDE+∠B,
∴∠1+∠B-∠CDE=∠CDE+∠B,
∴∠1=2∠CDE,
∴当∠α为定值时,∠CDE为定值,
故选B.
考点:等腰三角形的性质.
2.A
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
【详解】∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
【点睛】本题考查了角平分线的定义和三角形内角和定理,解决问题的关键是三角形外角性质以及角平分线的定义的运用.
3.D
【详解】分析: 根据无理数的三种形式求解.
详解:、、、(每两个1之间增加一个3)是无理数,共4个.
故选D.
点睛:本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
4.B
【详解】解:A.无限不循环小数是无理数,故A错误;
B.无理数是无限小数,正确;
C.实数分为正实数、负实数和0,故C错误;
D.互为相反数的两个无理数的和是0,不是无理数,故D错误.
故选B.
5.D
【分析】根据数轴上的数,右边的总比左边的大即可解答.
【详解】观察数轴可得:a<0<b,
∴选项A、B、C错误,选项D正确.
故选D.
【点睛】本题考查了数轴和有理数数的应用,解题的关键是掌握数轴上的数,右边的总比左边的大这一性质.
6.A
【分析】结合已知条件和全等三角形的判定方法,对所给的三个命题依次判定,即可解答..
【详解】①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选A.
【点睛】本题主要考查全等三角形的判定方法,要求学生能对常用的判定方法熟练掌握并能进行灵活运用.解决命题②时,可以用“倍长中线法”.
7.C
【分析】根据有数的乘方、立方根和平方根的知识即可判断.
【详解】A、,故选项A错误;
B、,故选项B错误;
C、,,故选项C正确;
D、=3,故选项D错误.
故选C.
【点睛】此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.
8.D
【分析】如图,设∠B′FE=x,根据折叠的性质得∠BFE=∠B′FE=x,∠AEF=∠A′EF,则∠BFC=x-18°,再由第2次折叠得到∠C′FB=∠BFC=x-18°,于是利用平角定义可计算出x=66°,接着根据平行线的性质得∠A′EF=180°-∠B′FE=114°,所以∠AEF=114°.
【详解】如图,设∠B′FE=x,
∵纸条沿EF折叠,
∴∠BFE=∠B′FE=x,∠AEF=∠A′EF,
∴∠BFC=∠BFE ∠CFE=x 18°,
∵纸条沿BF折叠,
∴∠C′FB=∠BFC=x 18°,
而∠B′FE+∠BFE+∠C′FB=180°,
∴x+x+x 18°=180°,解得x=66°,
∵A′D′∥B′C′,
∴∠A′EF=180° ∠B′FE=180° 66°=114°,
∴∠AEF=114°.
故答案选:D.
【点睛】本题考查了翻折变换(折叠问题)与平行线的性质,解题的关键是熟练的掌握翻折变换(折叠问题)与平行线的性质.
9.B
【分析】根据平行线的性质逐项判断即可.
【详解】A、∵AB//CD,
∴∠1+∠2=180°.故本选项不符合题意;
B、如图,∵AB//CD,
∴∠1=∠3.
∵∠2=∠3,
∴∠1=∠2.故本选项正确.
C、∵AB//CD,
∴∠BAD=∠CDA,不能得到∠1=∠2.故本选项不符合题意;
D、当梯形ABDC是等腰梯形时才有,∠1=∠2.故本选项不符合题意.
故选:B.
【点睛】本题考查平行线的性质,熟练掌握平行线的性质是解答的关键.
10.D
【分析】直接利用垂线段最短以及结合已知得出AP的取值范围进而得出答案.
【详解】∵过点A作AB⊥l于点B,AC=2AB,P在线段BC上连结AP,AB=3,∴AC=6,∴3≤AP≤6,故AP不可能是6.5.
故选D.
【点睛】本题考查了垂线段最短,正确得出AP的取值范围是解题的关键.
11.等腰直角三角形
【分析】设∠A=x,根据题意和三角形的内角和定理可得关于x的方程,解方程即可求出x,进而可得答案.
【详解】解:因为在△ABC中,∠A:∠B:∠C=1:1:2,
所以设∠A=x,则∠B=x,∠C=2x,
因为∠A+∠B+∠C=180°,
所以x+x+2x=180°,解得:x=45°,
所以∠A=45°,∠B=45°,∠C=90°,
所以这个三角形的形状为等腰直角三角形.
故答案为:等腰直角三角形.
【点睛】本题考查了三角形的内角和定理和特殊三角形的判定,属于基础题型,熟练掌握基本知识是解题的关键.
12.<
【分析】先把根号外的因式移入根号内,再比较大小即可.
【详解】∵=,=,<,
∴<,
故答案为:<
【点睛】本题考查了比较二次根式的大小,能选择适当的方法比较两个实数的大小是解此题的关键.
13.49
【分析】根据正数有两个平方根,它们互为相反数,先求出a的值,再求出这个数的平方.
【详解】解:因为一个非负数的平方根互为相反数,
所以a+3+2a-15=0
解得a=4
所以a+3=7
72=49.
即这个数是49.
故答案为49.
【点睛】本题考查了平方根的意义,根据正数的平方根互为相反数列出方程,是解决本题的关键.
14.
【分析】设正方形的边长为x,根据题意得,求解即可.
【详解】解:设正方形的边长为x,
由题意得,
∴x=(负值舍去),
故答案为:.
【点睛】此题考查平方根的实际应用,正确求一个数的平方根是解题的关键.
15.
【分析】根据二次根式乘除法运算法则进行计算即可得到答案.
【详解】解:
=
=.
故答案为:.
【点睛】此题主要考查了二次根式的乘除运算,掌握运算法则是解答此题的关键.
16.(答案不唯一)
【分析】本题需先根据已知条件,写出一个正数并且是无理数即可求出答案.
【详解】比0大的无理数有,等,
故答案为:(答案不唯一).
【点睛】本题主要考查无理数,用到的知识点是无理数的定义和实数的比较大小,在解题时根据正无理数的定义写出结果是解题关键.
17. 4; 230.
【分析】根据同旁内角的角的定义即可写出的所有同旁内角是,,,;根据三角形的内角和定理得,,据此求出,,,的和即可.
【详解】解:由图像可知图中与构成同旁内角的角有,,,,共计4个,
由三角形的内角和定理可得:
,
,
∴
故答案是:4,230.
【点睛】本题主要考查了同旁内角的角,三角形的内角和定理等知识点,熟悉相关知识点是解题的关键.
18.16
【分析】等式两边同时平方即可求出答案.
【详解】解:∵
∴
故答案为:16.
【点睛】此题主要考查了算术平方根,注意:一个非负数的算术平方根是非负数.
19.>
【分析】任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.
【详解】解:∵,
∴,
∴,
故答案为:>.
【点睛】本题主要考查了实数大小的比较,在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.
20.∠2+∠4=∠1+∠3
【分析】分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
【详解】解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
【点睛】本题考查的是平行线的性质,即两直线平行,内错角相等.
21.
【分析】根据数轴的特点即可求解.
【详解】∵实数在数轴上对应的点到原点的距离是,
∴a=±
∵a为正
∴
故答案为:.
【点睛】此题主要考查实数与数轴,解题的关键是熟知数轴的特点.
22.
【分析】将等式的左边展开,根据,是有理数求得a、b值,即可求解.
【详解】解:∵,且,是有理数,
∴a=﹣1,b=1,
∴ab=(﹣1)×1=﹣1,
故答案为:﹣1.
【点睛】本题考查实数的运算、代数式的求值,掌握实数的运算法则是解答的关键.
23.0或2
【分析】当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内;当三角形为直角三角形和锐角三角形时没有高在三角形外.
【详解】解:∵当三角形为直角三角形和锐角三角形时,没有高在三角形外;而当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内.
∴在三角形的三条高中,位于三角形外的可能条数是0或2条
故答案为0或2.
【点睛】此题主要考查了三角形的高的位置,不同形状的三角形,它的高的情况不同,要求学生必须熟练掌握.
24.
【分析】根据实数的性质及算术平方根的定义即可求解.
【详解】输入64时,取算术平方根为=8,为有理数;
再去算术平方根为=,为无理数,故输出
故答案为:.
【点睛】此题主要考查程序的计算,解题的关键是熟知实数的性质及算术平方根的定义.
25.
【分析】先求出根式里的数,再根据实数的性质进行化简.
【详解】
故答案为:.
【点睛】此题主要考查实数的运算,解题的关键是熟知实数的性质.
26.3
【分析】根据有效数字的定义即可求解.
【详解】的有效数字为6、1、0
故答案为:3.
【点睛】此题主要考查有效数字的个数,解题的关键是熟知有效数字的定义.
27.100
【分析】先计算,即可得到的值.
【详解】∵,
∴
∴=
故答案为:100.
【点睛】此题主要考查二次根式的运算,解题的关键是熟知其运算法则.
28.9
【分析】根据题意可得,即可得 , ,即可求解.
【详解】∵ ,
∴,
∴ , ,
∴ .
故答案为:
【点睛】本题主要考查了估算无理数的大小,解题的关键是正确估算出该无理数在哪两个连续的整数之间.
29.直角顶点
【分析】根据三角形高的概念解答即可.
【详解】解:∵直角三角形有两条高与直角边重合,
∴它们的交点是直角顶点.
故答案为:直角顶点.
【点睛】本题考查的是三角形的高的概念,注意:锐角三角形的三条高在三角形的内部,相交于三角形内一点;直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
30.4
【分析】根据同旁内角定义:两条直线被第三条直线所截,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进行分析即可.
【详解】解:∠1和∠2,∠1和∠3,∠2和∠3,∠4和∠5是同旁内角,共4对,
故答案为:4.
【点睛】此题主要考查了同旁内角的定义,关键是掌握同旁内角的边构成“U”形.
31.(1)与射线垂直,理由见解析;(2)的大小为或或.
【分析】(1)先根据平行线的性质、角平分线的定义得出,再根据角平分线的定义得出,最后根据三角形的外角性质、领补角的定义即可得出结论;
(2)先根据角平分线的定义、直角三角形的性质求出和的度数,再根据“中有两个相等的角”分三种情况,然后分别根据三角形的外角性质、角的和差求解即可得.
【详解】(1)与射线垂直,理由如下:
如图1,
平分,平分
,
由三角形的外角性质得:
又
即与射线垂直;
(2)平分,
如图2,由题意,分以下三种情况:
①当时
(三角形的外角性质)
②当时
③当时
则
解得
综上,的大小为或或.
【点睛】本题考查了平行线的性质、垂直的定义、三角形的外角性质等知识点,较难的是题(2),依据题意,正确分三种情况讨论是解题关键.
32.(1)见解析;(2)见解析;(3)见解析;(4)0
【分析】(1)根据角平分线的作法,即可得到的角平分线BD;
(2)根据垂直平分线的作法,即可得到边的中垂线;
(3)根据同位角相等,两直线平行,作即可得到;
(4)由点F在边BC上,可得点F到边BC的距离为0.
【详解】解:(1)如图所示,射线即为所求;
(2)如图所示,直线即为所求;
(3)如图所示,直线即为所求;
(4)∵点F在边BC上,
∴点到边的距离为0,
故答案为:0.
【点睛】本题主要考查了尺规作图-基本作图和点到直线的距离,熟练掌握角平分线的作法、垂直平分线的作法和作一个角等于已知角的作法是解题的关键.
33.
【分析】先计算分数指数幂、绝对值和零指数幂,再进一步计算即可求得结果.
【详解】原式
【点睛】本题主要考查实数的运算,解题的关键是熟练掌握分数指数幂、绝对值和零指数幂.
34.(1)120;(2)灯转动100秒,两灯的光束互相平行;(3)在转动过程中,和关系不会变化,且有,理由见解析.
【分析】(1)先根据角的倍差求出的度数,再根据平行线的性质即可得;
(2)设A灯转动时间为t秒,先求出两个临界位置:灯射线从开始顺时针旋转至、灯射线从开始顺时针旋转至,再分三种情况,分别利用平行线的性质列出等式求解即可得;
(3)先根据角的和差求出,再根据三角形的内角和定理可得,然后根据角的和差可得,由此即可得.
【详解】(1)∵,
∴
(两直线平行,内错角相等)
故答案为:120;
(2)设A灯转动时间为t秒
灯射线从开始顺时针旋转至所需时间为(秒),灯射线从开始顺时针旋转至所需时间为(秒)
灯射线从开始顺时针旋转至所需时间为(秒)
则t的取值范围为,即
由题意,分以下三种情况:
①当时,如图1所示
∵
∴
∵
∴
∴
∴
解得
此时,
即两灯的光束重合,不符题意,舍去
②当时,如图2所示,此时灯A射线未从AN回转
∵
∴
∵
∴
∴
∴
解得(不符题设,舍去)
③当时,如图2所示,此时灯A射线旋转至AN,并已开始回转
∵
∴
∵
∴
∴
∴
解得,符合题设
综上,灯转动100秒,两灯的光束互相平行;
(3)和关系不会变化,且有,理由如下:
设灯A射线转动时间为t秒
∵
∴
又∵
∴
∴
∴,即
故在转动过程中,和关系不会变化,且有.
【点睛】本题考查了平行线的性质、角的和差倍分、三角形的内角和定理等知识点,较难的是题(2),依据题意,找出两个临界位置,进而分三种情况讨论是解题关键.
35.
【分析】根据负指数幂、平方根与立方根、二次根式的加减法、除法运算计算即可.
【详解】原式
.
【点睛】本题考查了负指数幂、平方根与立方根、二次根式的加减法、除法运算,熟记各运算法则是解题关键.
36.(1);(2)直角边的平方和等于斜边的平方;(3)见解析;(4).
【分析】(1)观察已知各式,归纳总结规律即可得;
(2)根据等式和图形即可得;
(3)先作的垂线,再在垂线上截取,连接,可得,同理可作出点,连接即为所求;
(4)先分别求出的值,再归纳总结出一般规律得出的值,从而可得的值,然后代入求和即可.
【详解】(1)观察已知各式可得,各式的变化规律为
故答案为:;
(2)结合等式和图形可得,直角三角形两条直角边与斜边的关系为:直角边的平方和等于斜边的平方
故答案为:直角边的平方和等于斜边的平方;
(3)先作的垂线,再在垂线上截取,连接,即可得,同理可作点,连接,则即为所求,如图所示:
(4)
归纳类推得:
当时,
则
.
【点睛】本题考查了算术平方根、勾股定理等知识点,读懂题意,正确归纳类推出一般规律是解题关键.
37.见解析
【分析】根据角平分线定义和已知求出∠1=∠3,推出∠2=∠3,根据平行线的判定推出即可.
【详解】∵DE平分∠CDA(已知),
∴(角平分线的定义),
∵BF平分∠CBA(已知),
∴(角平分线的定义),
∵∠CDA=∠CBA(已知),
∴∠1=∠3(等量代换),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴DE//FB(同位角相等,两直线平行).
【点睛】本题考查了平行线的判定和角平分线定义的应用,注意:同位角相等,两直线平行.
38.已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等
【分析】先证得AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
【详解】∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD(等量代换),
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等.
【点睛】本题考查了平行线的性质和判定,垂直定义,补角定义的应用,能综合运用定理进行推理是解此题的关键.
39.6
【分析】逆用积的乘方,再运用幂的乘方运算法则计算即可.
【详解】
.
【点睛】本题考查了逆用积的乘方,运用幂的乘方运算法则计算是解题的关键.
40.(1)作图见解析;(2)作图见解析;(3);(4)
【分析】(1)过点P作∠OPC=90°,交OA于C即可;
(2)过点P作∠PHO=90°交OA于H即可;
(3)根据点到直线的距离定义,可得线段PH的长度是点到直线的距离.
(4)垂线段最短的性质可得,线段PC、PH、OC这三条线段大小关系是PH
(2)过点P作∠PHO=90°交OA于H点,如图所示;
(3)根据点到直线的距离定义,
可得线段PH的长度是点到直线的距离.
故答案为:PH
(4)根据垂线段最短性质可得
在Rt△PHC中,PC>PH
在Rt△OHP中,OC>PC
∴线段PC、PH、OC这三条线段大小关系是PH
41.
【分析】根据二次根式的运算法则,先算括号里的,再算乘除,最后算加减,即可求解.
【详解】解:原式
故答案为:
【点睛】本题考查了二次根式的混合运算,在运算中要掌握好运算的顺序及运算规律.
42.3
【分析】根据相反数的性质化简得,再代入原式求解即可.
【详解】解:与互为相反数,
与互为相反数,即
化简得
即
原式
【点睛】本题考查了分式的运算问题,掌握相反数的性质是解题的关键.
43.见解析
【分析】根据中点定义求出AC=CB,两直线平行,同位角相等,求出∠ACD=∠B,然后证明△ACD和△CBE全等,再利用全等三角形的对应角相等进行解答.
【详解】解:∵C是AB的中点,
∴AC=CB(线段中点的定义).)
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
∴∠D=∠E(全等三角形的对应角相等).
【点睛】本题主要考查了全等三角形的判定与全等三角形的性质,确定用SAS定理进行证明是关键.
44.4
【分析】首先将每个根式化为以2为底数的幂,然后根据同底数幂的除法与乘法运算法则求解即可求得答案.
【详解】解:原式
【点睛】此题考查了分数指数幂的知识.此题难度适中,解题的关键是掌握分数指数幂的定义,同底数幂的除法与乘法运算法则.
45.(1)画图见解析;(2)①,②,③
【分析】(1)根据角、线段、垂线、平行线的画法即可得;
(2)①根据点到点的距离定义即可得;
②根据点到直线的距离定义即可得;
③根据平行线间的距离即可得.
【详解】(1)根据角、线段、垂线、平行线的画法,作图结果如下:
(2)①线段长AC是点到点的距离
②线段长BD是点到直线的距离
③
则线段长ND是平行线和间的距离
故答案为:①,②,③.
【点睛】本题考查了角、线段、垂线、平行线的画法,理解题意,正确画出图形是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
