第六章 勾股定理[上学期]
图片预览


文档简介
第六章 勾股定理
一、基础知识梳理
1.勾股定理
若a、b、c分别为直角三角形的两直角边与斜边,则满足a2+b2=c2.
2.直角三角形的判别方法
已知三角形的三边a、b、c,若满足a2+b2=c2,则这个三角形为直角三角形.
3.立体图形与平面图形的转化
(1)表面路径最短的问题,一般把表面展开,展成平面后运用勾股定理.
(2)空间距离问题,一般从立体图形中找到直角三角形并运用勾股定理.
二、考点与命题趋向分析
(一)能力
体验勾股定理的探索过程,会运用勾股定理解决简单的问题;会用勾股定理的逆定理判定直角三角形
(二)命题趋向分析
本章内容是已知直角三角形的两边求第三边或利用勾股定理得到有关线段之间的关系,是中考内容的重中之重,出现频率较高,一般以选择题、填空题或计算题的形式出现,有时也作为一道综合题的一个考查点出现.
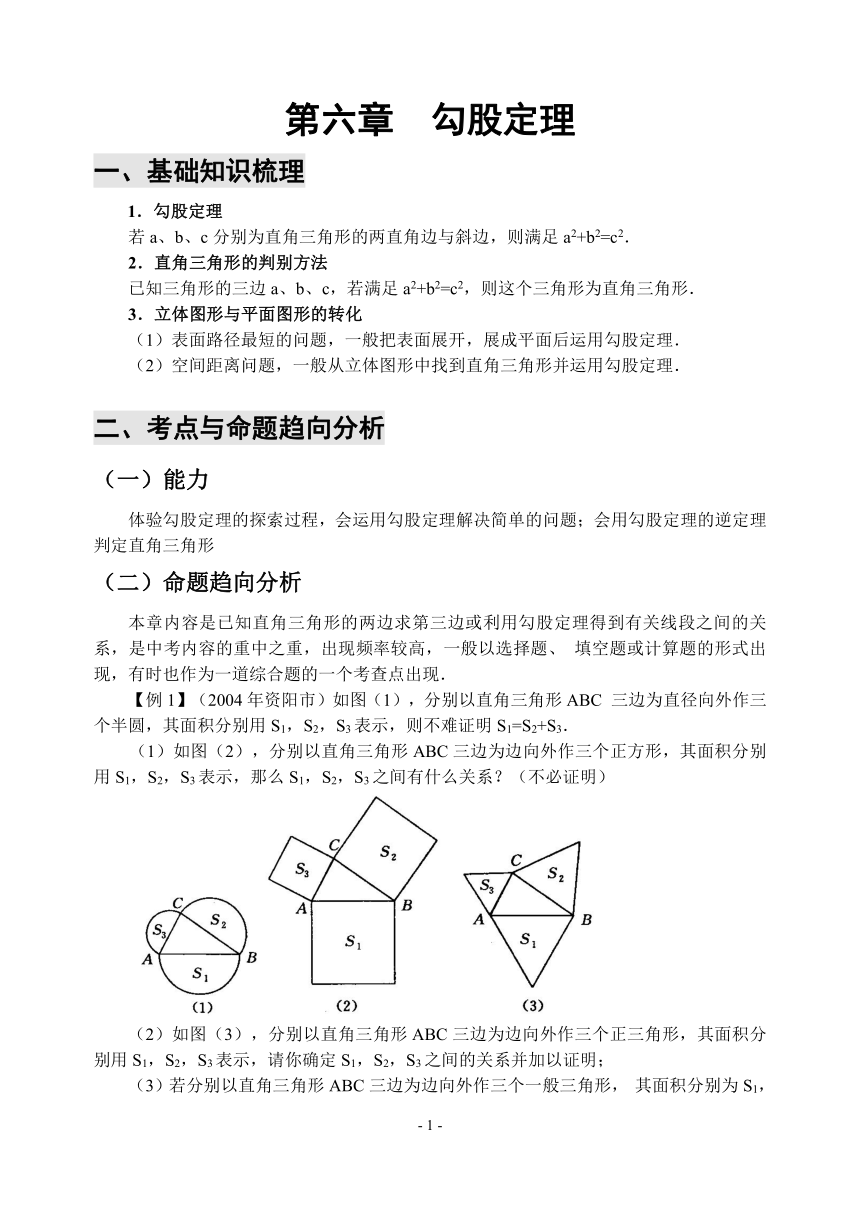
【例1】(2004年资阳市)如图(1),分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.
(1)如图(2),分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系?(不必证明)
(2)如图(3),分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明;
(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别为S1,S2,S3表示.为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
(4)类比(1)(2)(3)的结论,请你总结出一个更具有一般意义的结论.
【思路分析】设直角三角形ABC的三边BC、CA、AB的长分别为a,b,c,则c2=a2+b2.利用勾股定理本题很容易完成.
【解】设直角三角形ABC的三边BC、CA、AB的长分别为a,b,c,则c2=a2+b2.
(1)S1=S2+S3.
(2)S1=S2+S3.证明如下:
显然S1=C2,S2=a2,S3=b2,
∵c2=a2+b2
∴S2+S3=(a2+b2)=c2=S1
(3)当所作的三个三角形相似时,S1=S2+S3,证明如下:
∵所作三个三角形相似,
∴,
∴==1,
∴S2+S3=S1
(4)分别以直角三角形ABC三边一边向外作相似图形,其面积分别用S1,S2,S3表示,则S1=S2+S3.
三、解题方法与技巧
方法1:关注最长边
【例1】已知三角形的三边长a=,b=,c=1,这个三角形是直角三角形吗?
【思路分析】a2=,b2=,c2=1.
虽然a2+b2≠c2,但不能急于判断这个三角形不是直角三角形.因为不难计算a2+c2=b2,这个三角形是直角三角形.
【解】∵a2+c2=+1==b2
【规律总结】1.在利用勾股定理的逆定理判断是否是直角三角形时,应先找最长边,而不要受思维定势的影响.
2.常见的勾股数3,4,5三边分别乘以,则可得,1,,可见这个三角形是直角三角形.
方法2:运用数形结合思想证明勾股定理
【例2】(2004年济南市)如图1是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,图2是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图,写出它是什么图形;
(2)用这个图形证明勾股定理;
(3)假设图1中的直角三角形有若干个.你能运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
(1) (2) (3)
【思路分析】(1)利用两个图形中有相同的线段c,并注意运用直角三角形两锐角互余,可拼成图3的直角梯形,这是美国总统Carfield于1876年给出的一种验证勾股定理的方法.
(2)利用面积关系,从两个不同的角度即可说明勾股定理.
(3)拼图方案较多,能说明勾股定理即可.
【解】(1)用所给三角形可接成如图所示的图形,它是一个直角梯形.
(2)∵S梯形=(a+b)(a+b)=(a+b)2
S梯形=ab×2+c2=ab+c2
∴(a+b)2=ab+c2
整理,得a2+b2=c2.
(3)拼图方案较多,现给出几种,如图所示:
方法3:立体图形问题转化为平面图形问题
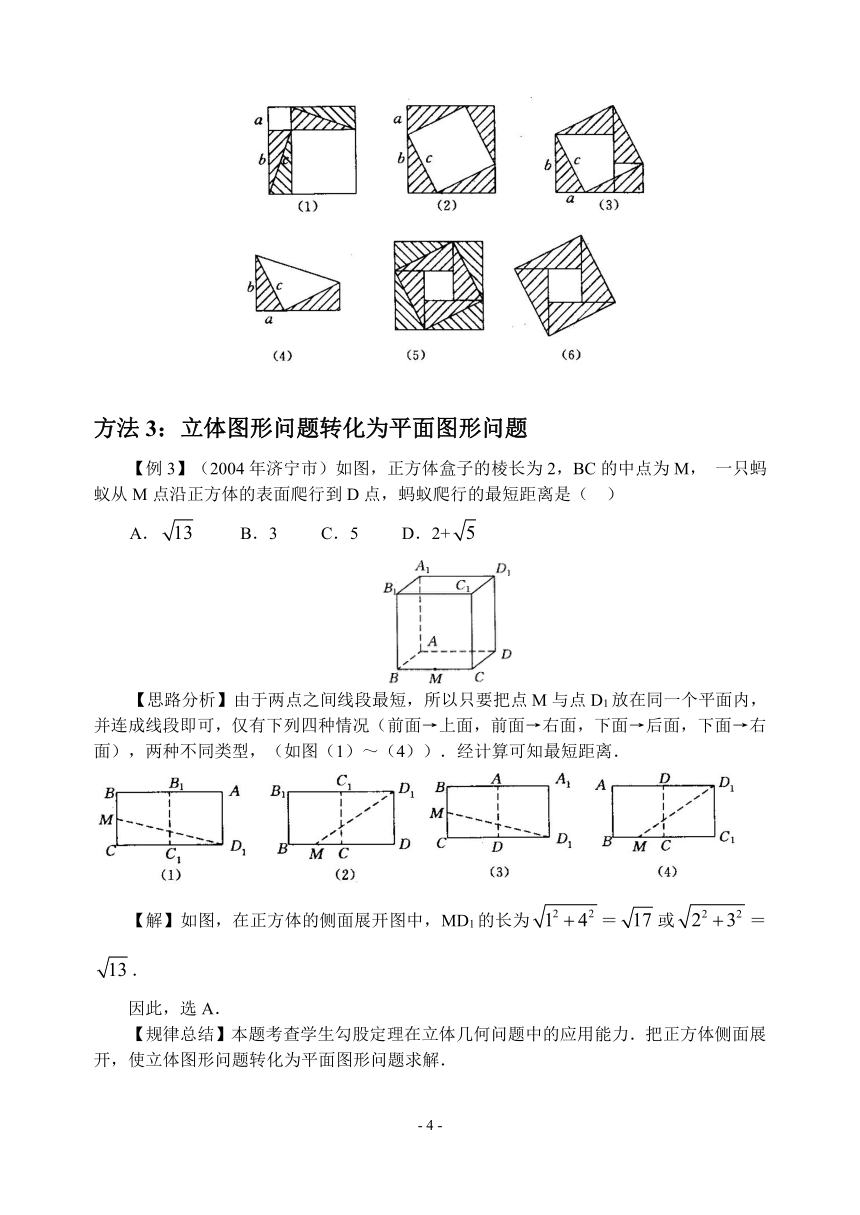
【例3】(2004年济宁市)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬行到D点,蚂蚁爬行的最短距离是( )
A. B.3 C.5 D.2+
【思路分析】由于两点之间线段最短,所以只要把点M与点D1放在同一个平面内,并连成线段即可,仅有下列四种情况(前面→上面,前面→右面,下面→后面,下面→右面),两种不同类型,(如图(1)~(4)).经计算可知最短距离.
【解】如图,在正方体的侧面展开图中,MD1的长为=或=.
因此,选A.
【规律总结】本题考查学生勾股定理在立体几何问题中的应用能力.把正方体侧面展开,使立体图形问题转化为平面图形问题求解.
方法4:运用勾股定理解决实际问题
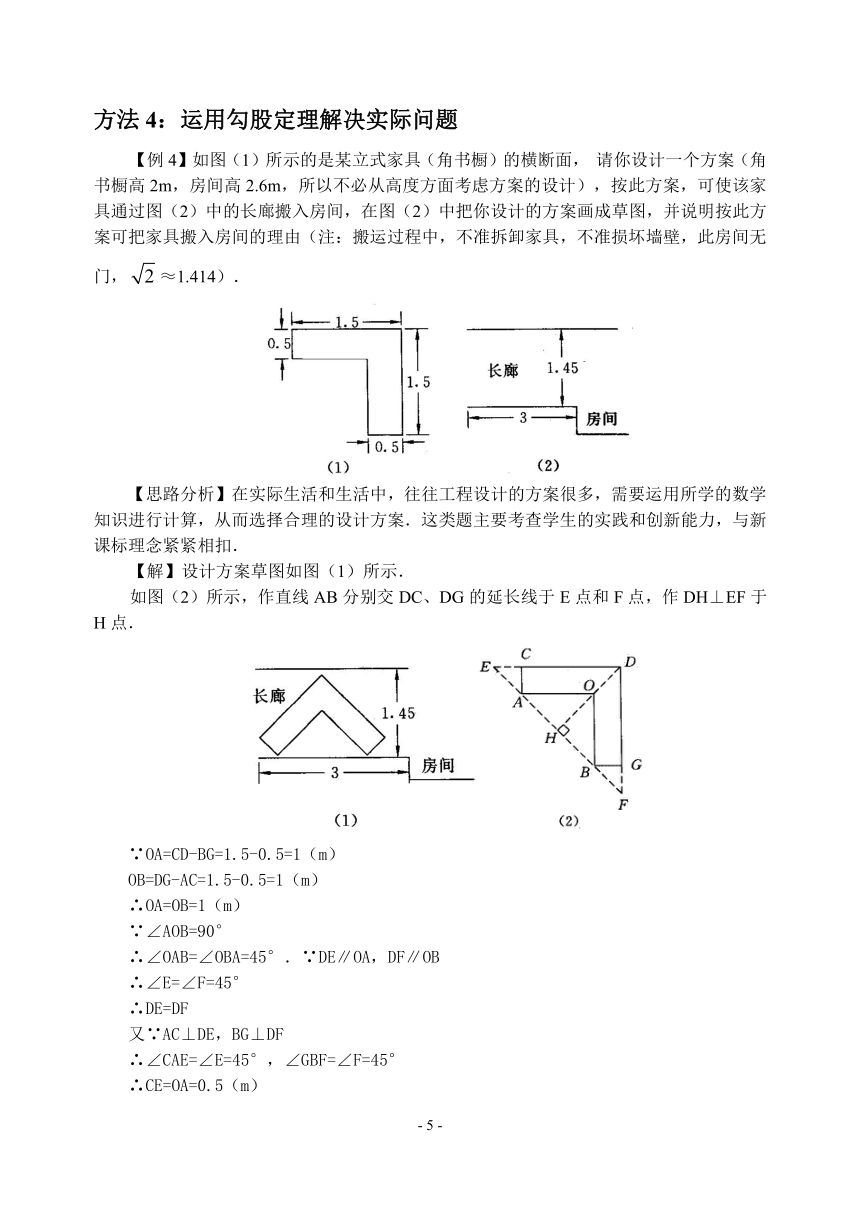
【例4】如图(1)所示的是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2m,房间高2.6m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图(2)中的长廊搬入房间,在图(2)中把你设计的方案画成草图,并说明按此方案可把家具搬入房间的理由(注:搬运过程中,不准拆卸家具,不准损坏墙壁,此房间无门,≈1.414).
【思路分析】在实际生活和生活中,往往工程设计的方案很多,需要运用所学的数学知识进行计算,从而选择合理的设计方案.这类题主要考查学生的实践和创新能力,与新课标理念紧紧相扣.
【解】设计方案草图如图(1)所示.
如图(2)所示,作直线AB分别交DC、DG的延长线于E点和F点,作DH⊥EF于H点.
∵OA=CD-BG=1.5-0.5=1(m)
OB=DG-AC=1.5-0.5=1(m)
∴OA=OB=1(m)
∵∠AOB=90°
∴∠OAB=∠OBA=45°.∵DE∥OA,DF∥OB
∴∠E=∠F=45°
∴DE=DF
又∵AC⊥DE,BG⊥DF
∴∠CAE=∠E=45°,∠GBF=∠F=45°
∴CE=OA=0.5(m)
∴DE=DC+CE=1.5+0.5=2(m)
DF=DG+GF=1.5+0.5=2(m)
∵∠EDF=90°
∴EF2=DE2+DF2=22+22=8
∴EF=2
∵S△DEF=DE·DF=EF·DH
∴×2×2=×2×DH
∴DH=≈1.414<1.45
∴可以按照方案设计图将家具搬入房间.
方法5:总结规律,找出常见勾股数
序号 a b c
1 3=2×1+1 4=2×1×(1+1) 5=2×1×(1+1)+1
2 5=2×2+1 12=2×2×(2+1) 13=2×2×(2+1)+1
3 7=2×3+1 24=2×3×(3+1) 25=2×3×(3+1)+1
4 9=2×4+1 40=2×4×(4+1) 41=2×4×(4+1)+1
… … … …
n 2n+1 2n(n+1) 2n(n+1)+1
序号 a b c
1 6=4×1+2 8=4×1×(1+1) 10=4×1×(1+1)+2
2 10=4×2+2 24=4×2×(2+1) 26=4×2×(2+1)+2
3 14=4×3+2 48=4×3×(3+1) 50=4×3×(3+1)+2
4 18=4×4+2 80=4×4×(4+1) 82=4×4×(4+1)+2
… … … …
n 4n+2 4n(n+1) 4n(n+1)+2
四、中考试题归类解析
(一)勾股定理
【例1】(2004,北京市)已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
【思路分析】利用∠B=30°,CD=6可求出BC.然后再用BC和∠B=30°求出AC,最后利用勾股定理可求出AB.
【解】∵∠B=30° ∠CDB=90° CD=6
∴BC=12
又∵tan∠B=
∴AC=BC·tan∠B=12×=4
AB===8
【规律总结】此题解法很多,利用三角函数解是最为简便的.
【例2】(2004,四川省)如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知AB=4,那么AD_______.
【思路分析】由∠B=30°,AB=4可求出AC,再由AC、∠DAC=30°可求CD,然后由勾股定理可求出AD.
【解】∵∠ACB=90° ∠B=30° AB=4
∴AC=AB=×4=2
又∵∠BAC=60° AD是∠BAC平分线
∴∠CAD=30°
∵∠ACD=90° ∠CAD=30° AC=2
∴tan∠CAD=
∴CD=AC.tan∠CAD=2×=2
∴AD====4
【规律总结】本题当求出AC的长时,可利用三角函数直接求出AD.且比利用勾股定理简单.
(二)直角三角形全等
【例1】(2004,乌鲁木齐市)如图,在△ABC中,∠B=∠C,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.
求证:(1)△BDE≌△CDF。
(2)当△ABC是直角三角形时,四边形AEDF是正方形.
【思路分析】(1)由D是BC中点可得BD=DC,而∠B=∠C、∠BED=∠CFD可证出△BED≌△CDF.
(2)当△ABC是直角三角形时可得到四边形AEDF是矩形,又因为DE=DF所以能够得到四边形AEDF是正方形.
证明:(1)∵DE⊥AB,DF⊥AC
∴∠BED=∠CFD=90°
又∵∠B=∠C BD=CD
∴△BDE≌△CDF
(2)∵∠DEA=∠DFA=∠A=90°
∴四边形AEDF是矩形
又∵DE=DF
∴矩形AEDF是正方形
【规律总结】证明两个直角三角形全等不能只想到用(LH)来证明,应该想到证明一般三角形全等的方法也适用
【例2】(2004,徐州)已知:如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足DE=BF,求证:AF=CE,且AB∥CD.
【思路分析】由DE⊥AC、BF⊥AC可得∠DEC=∠BFA=90°,加上AB=CD、DE=BF能推出Rt△CDE≌Rt△ABF下,当两个直角三角形全等了可得∠C=∠A,所以DC∥AB.
证明:∵DE⊥AC,BF⊥AC
∴∠AFB=∠CED=90°
在Rt△AFB和Rt△CED中
∵AB=CD,BF=DE
∴Rt△AFB≌Rt△CED
∴AF=CE,∠A=∠C
∴AB∥CD
【规律总结】要证两个直角三角形的全等,首先应该想到用(HL)去证明,当用(HL)证明不出来时再考虑用别的方法.
五、中考试题集萃
一、填空题
1.(2004,临汾市)如图1,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC=_______度.
(1) (2) (3) (4)
2.(2004,青海省湟中县)如图2,已知:在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,AC=10,则AB_______.
3.(2004,南通市)如图3,为了求出湖两岸A、B两点之间的距离,观测者从测点A、B分别测得∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间的距离为______m.(结果保留根号).
4.(2004,昆明市)如图4,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S2_____.
5.(2004,杭州)在第六册课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽,它的主体图案是由一连串如图所示的直角三角形演化而成的,设其中的第一个直角三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3=A3A4…=A8A9=1,请你先把图中其他8条线段的长计算出来,填在下面的表格中,然后再计算这8条线段的长的乘积.
OA2 OA3 OA4 OA5 OA6 OA7 OA8 OA9
二、选择题
1.(2004,黑龙江)如图在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
A.15° B.20° C.25° D.30°
(5) (6) (7)
2.(2004,杭州)如图,在Rt△ABC中,AF是斜边BC上的高线,且BD=DC=FC=1,则AC的长为( )
A. B. C. D.
3.(2004,包头市)如图,为了确定一条河的宽度AB,可以在点B一测的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
A.40米 B.40米 C.20米 D.20米
三、解答题
1.(2004,青海)如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D,求证:OC=OD.
2.(2004,荆门)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法,如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积证明勾股定理:a2+b2=c2.
答案:
一、填空题:
1.35 2.6 3.80 4.144
5.表内从左到右依次为,,2,,,,2,3;
它们的乘积为72
二、选择题:1.D 2.A 3.A
三、解答题:
1.证△OCE≌△ODE.
2.矩形ABCD绕点A旋转90°,AC旋转到AC′的位置,则∠CAC′=90°
∴S梯形BCC‘D’=S△ABC+S△CAC‘+S△D’AC‘
=ab+c2+ab
=
∴=
∴a2+b2=c2.毛
- 1 -
一、基础知识梳理
1.勾股定理
若a、b、c分别为直角三角形的两直角边与斜边,则满足a2+b2=c2.
2.直角三角形的判别方法
已知三角形的三边a、b、c,若满足a2+b2=c2,则这个三角形为直角三角形.
3.立体图形与平面图形的转化
(1)表面路径最短的问题,一般把表面展开,展成平面后运用勾股定理.
(2)空间距离问题,一般从立体图形中找到直角三角形并运用勾股定理.
二、考点与命题趋向分析
(一)能力
体验勾股定理的探索过程,会运用勾股定理解决简单的问题;会用勾股定理的逆定理判定直角三角形
(二)命题趋向分析
本章内容是已知直角三角形的两边求第三边或利用勾股定理得到有关线段之间的关系,是中考内容的重中之重,出现频率较高,一般以选择题、填空题或计算题的形式出现,有时也作为一道综合题的一个考查点出现.
【例1】(2004年资阳市)如图(1),分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.
(1)如图(2),分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系?(不必证明)
(2)如图(3),分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明;
(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别为S1,S2,S3表示.为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
(4)类比(1)(2)(3)的结论,请你总结出一个更具有一般意义的结论.
【思路分析】设直角三角形ABC的三边BC、CA、AB的长分别为a,b,c,则c2=a2+b2.利用勾股定理本题很容易完成.
【解】设直角三角形ABC的三边BC、CA、AB的长分别为a,b,c,则c2=a2+b2.
(1)S1=S2+S3.
(2)S1=S2+S3.证明如下:
显然S1=C2,S2=a2,S3=b2,
∵c2=a2+b2
∴S2+S3=(a2+b2)=c2=S1
(3)当所作的三个三角形相似时,S1=S2+S3,证明如下:
∵所作三个三角形相似,
∴,
∴==1,
∴S2+S3=S1
(4)分别以直角三角形ABC三边一边向外作相似图形,其面积分别用S1,S2,S3表示,则S1=S2+S3.
三、解题方法与技巧
方法1:关注最长边
【例1】已知三角形的三边长a=,b=,c=1,这个三角形是直角三角形吗?
【思路分析】a2=,b2=,c2=1.
虽然a2+b2≠c2,但不能急于判断这个三角形不是直角三角形.因为不难计算a2+c2=b2,这个三角形是直角三角形.
【解】∵a2+c2=+1==b2
【规律总结】1.在利用勾股定理的逆定理判断是否是直角三角形时,应先找最长边,而不要受思维定势的影响.
2.常见的勾股数3,4,5三边分别乘以,则可得,1,,可见这个三角形是直角三角形.
方法2:运用数形结合思想证明勾股定理
【例2】(2004年济南市)如图1是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,图2是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图,写出它是什么图形;
(2)用这个图形证明勾股定理;
(3)假设图1中的直角三角形有若干个.你能运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
(1) (2) (3)
【思路分析】(1)利用两个图形中有相同的线段c,并注意运用直角三角形两锐角互余,可拼成图3的直角梯形,这是美国总统Carfield于1876年给出的一种验证勾股定理的方法.
(2)利用面积关系,从两个不同的角度即可说明勾股定理.
(3)拼图方案较多,能说明勾股定理即可.
【解】(1)用所给三角形可接成如图所示的图形,它是一个直角梯形.
(2)∵S梯形=(a+b)(a+b)=(a+b)2
S梯形=ab×2+c2=ab+c2
∴(a+b)2=ab+c2
整理,得a2+b2=c2.
(3)拼图方案较多,现给出几种,如图所示:
方法3:立体图形问题转化为平面图形问题
【例3】(2004年济宁市)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬行到D点,蚂蚁爬行的最短距离是( )
A. B.3 C.5 D.2+
【思路分析】由于两点之间线段最短,所以只要把点M与点D1放在同一个平面内,并连成线段即可,仅有下列四种情况(前面→上面,前面→右面,下面→后面,下面→右面),两种不同类型,(如图(1)~(4)).经计算可知最短距离.
【解】如图,在正方体的侧面展开图中,MD1的长为=或=.
因此,选A.
【规律总结】本题考查学生勾股定理在立体几何问题中的应用能力.把正方体侧面展开,使立体图形问题转化为平面图形问题求解.
方法4:运用勾股定理解决实际问题
【例4】如图(1)所示的是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2m,房间高2.6m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图(2)中的长廊搬入房间,在图(2)中把你设计的方案画成草图,并说明按此方案可把家具搬入房间的理由(注:搬运过程中,不准拆卸家具,不准损坏墙壁,此房间无门,≈1.414).
【思路分析】在实际生活和生活中,往往工程设计的方案很多,需要运用所学的数学知识进行计算,从而选择合理的设计方案.这类题主要考查学生的实践和创新能力,与新课标理念紧紧相扣.
【解】设计方案草图如图(1)所示.
如图(2)所示,作直线AB分别交DC、DG的延长线于E点和F点,作DH⊥EF于H点.
∵OA=CD-BG=1.5-0.5=1(m)
OB=DG-AC=1.5-0.5=1(m)
∴OA=OB=1(m)
∵∠AOB=90°
∴∠OAB=∠OBA=45°.∵DE∥OA,DF∥OB
∴∠E=∠F=45°
∴DE=DF
又∵AC⊥DE,BG⊥DF
∴∠CAE=∠E=45°,∠GBF=∠F=45°
∴CE=OA=0.5(m)
∴DE=DC+CE=1.5+0.5=2(m)
DF=DG+GF=1.5+0.5=2(m)
∵∠EDF=90°
∴EF2=DE2+DF2=22+22=8
∴EF=2
∵S△DEF=DE·DF=EF·DH
∴×2×2=×2×DH
∴DH=≈1.414<1.45
∴可以按照方案设计图将家具搬入房间.
方法5:总结规律,找出常见勾股数
序号 a b c
1 3=2×1+1 4=2×1×(1+1) 5=2×1×(1+1)+1
2 5=2×2+1 12=2×2×(2+1) 13=2×2×(2+1)+1
3 7=2×3+1 24=2×3×(3+1) 25=2×3×(3+1)+1
4 9=2×4+1 40=2×4×(4+1) 41=2×4×(4+1)+1
… … … …
n 2n+1 2n(n+1) 2n(n+1)+1
序号 a b c
1 6=4×1+2 8=4×1×(1+1) 10=4×1×(1+1)+2
2 10=4×2+2 24=4×2×(2+1) 26=4×2×(2+1)+2
3 14=4×3+2 48=4×3×(3+1) 50=4×3×(3+1)+2
4 18=4×4+2 80=4×4×(4+1) 82=4×4×(4+1)+2
… … … …
n 4n+2 4n(n+1) 4n(n+1)+2
四、中考试题归类解析
(一)勾股定理
【例1】(2004,北京市)已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
【思路分析】利用∠B=30°,CD=6可求出BC.然后再用BC和∠B=30°求出AC,最后利用勾股定理可求出AB.
【解】∵∠B=30° ∠CDB=90° CD=6
∴BC=12
又∵tan∠B=
∴AC=BC·tan∠B=12×=4
AB===8
【规律总结】此题解法很多,利用三角函数解是最为简便的.
【例2】(2004,四川省)如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知AB=4,那么AD_______.
【思路分析】由∠B=30°,AB=4可求出AC,再由AC、∠DAC=30°可求CD,然后由勾股定理可求出AD.
【解】∵∠ACB=90° ∠B=30° AB=4
∴AC=AB=×4=2
又∵∠BAC=60° AD是∠BAC平分线
∴∠CAD=30°
∵∠ACD=90° ∠CAD=30° AC=2
∴tan∠CAD=
∴CD=AC.tan∠CAD=2×=2
∴AD====4
【规律总结】本题当求出AC的长时,可利用三角函数直接求出AD.且比利用勾股定理简单.
(二)直角三角形全等
【例1】(2004,乌鲁木齐市)如图,在△ABC中,∠B=∠C,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.
求证:(1)△BDE≌△CDF。
(2)当△ABC是直角三角形时,四边形AEDF是正方形.
【思路分析】(1)由D是BC中点可得BD=DC,而∠B=∠C、∠BED=∠CFD可证出△BED≌△CDF.
(2)当△ABC是直角三角形时可得到四边形AEDF是矩形,又因为DE=DF所以能够得到四边形AEDF是正方形.
证明:(1)∵DE⊥AB,DF⊥AC
∴∠BED=∠CFD=90°
又∵∠B=∠C BD=CD
∴△BDE≌△CDF
(2)∵∠DEA=∠DFA=∠A=90°
∴四边形AEDF是矩形
又∵DE=DF
∴矩形AEDF是正方形
【规律总结】证明两个直角三角形全等不能只想到用(LH)来证明,应该想到证明一般三角形全等的方法也适用
【例2】(2004,徐州)已知:如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足DE=BF,求证:AF=CE,且AB∥CD.
【思路分析】由DE⊥AC、BF⊥AC可得∠DEC=∠BFA=90°,加上AB=CD、DE=BF能推出Rt△CDE≌Rt△ABF下,当两个直角三角形全等了可得∠C=∠A,所以DC∥AB.
证明:∵DE⊥AC,BF⊥AC
∴∠AFB=∠CED=90°
在Rt△AFB和Rt△CED中
∵AB=CD,BF=DE
∴Rt△AFB≌Rt△CED
∴AF=CE,∠A=∠C
∴AB∥CD
【规律总结】要证两个直角三角形的全等,首先应该想到用(HL)去证明,当用(HL)证明不出来时再考虑用别的方法.
五、中考试题集萃
一、填空题
1.(2004,临汾市)如图1,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC=_______度.
(1) (2) (3) (4)
2.(2004,青海省湟中县)如图2,已知:在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,AC=10,则AB_______.
3.(2004,南通市)如图3,为了求出湖两岸A、B两点之间的距离,观测者从测点A、B分别测得∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间的距离为______m.(结果保留根号).
4.(2004,昆明市)如图4,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S2_____.
5.(2004,杭州)在第六册课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽,它的主体图案是由一连串如图所示的直角三角形演化而成的,设其中的第一个直角三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3=A3A4…=A8A9=1,请你先把图中其他8条线段的长计算出来,填在下面的表格中,然后再计算这8条线段的长的乘积.
OA2 OA3 OA4 OA5 OA6 OA7 OA8 OA9
二、选择题
1.(2004,黑龙江)如图在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
A.15° B.20° C.25° D.30°
(5) (6) (7)
2.(2004,杭州)如图,在Rt△ABC中,AF是斜边BC上的高线,且BD=DC=FC=1,则AC的长为( )
A. B. C. D.
3.(2004,包头市)如图,为了确定一条河的宽度AB,可以在点B一测的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
A.40米 B.40米 C.20米 D.20米
三、解答题
1.(2004,青海)如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D,求证:OC=OD.
2.(2004,荆门)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法,如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积证明勾股定理:a2+b2=c2.
答案:
一、填空题:
1.35 2.6 3.80 4.144
5.表内从左到右依次为,,2,,,,2,3;
它们的乘积为72
二、选择题:1.D 2.A 3.A
三、解答题:
1.证△OCE≌△ODE.
2.矩形ABCD绕点A旋转90°,AC旋转到AC′的位置,则∠CAC′=90°
∴S梯形BCC‘D’=S△ABC+S△CAC‘+S△D’AC‘
=ab+c2+ab
=
∴=
∴a2+b2=c2.毛
- 1 -
