勾股定理2[上学期]
图片预览

文档简介
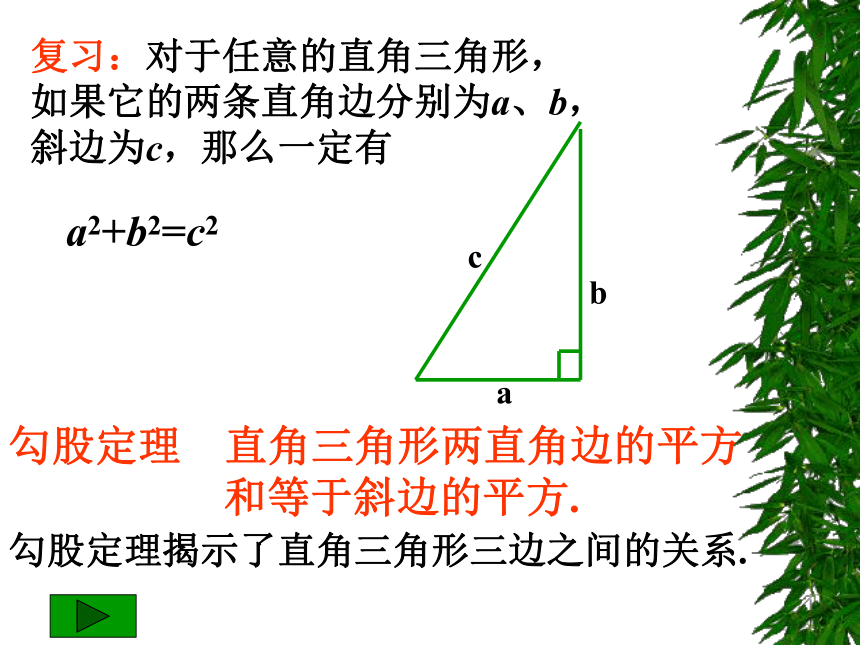
课件9张PPT。勾股定理2复习:对于任意的直角三角形,
如果它的两条直角边分别为a、b,
斜边为c,那么一定有
a2+b2=c2
勾股定理 直角三角形两直角边的平方
和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
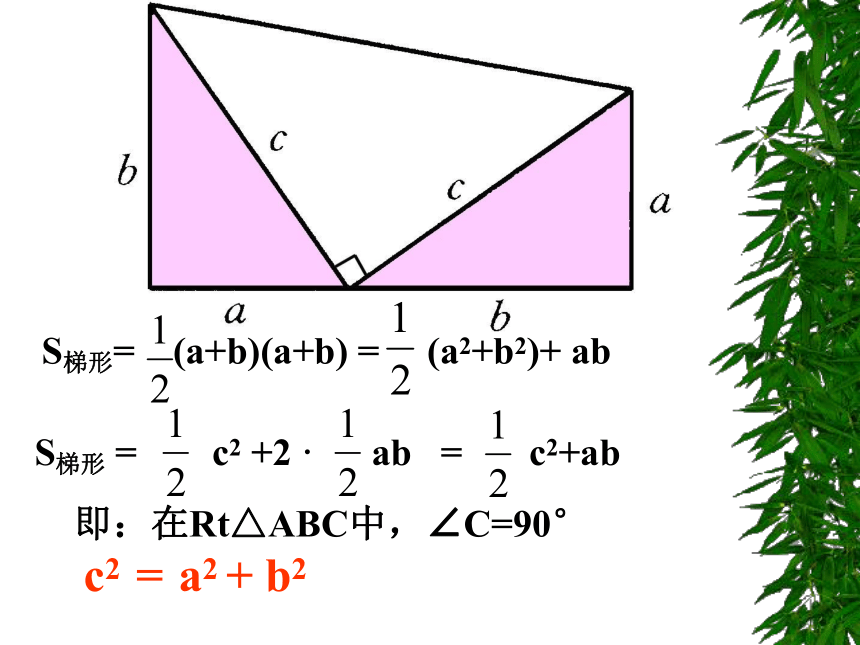
S梯形= (a+b)(a+b) = (a2+b2)+ abS梯形 = c2 +2 · ab = c2+ab 即:在Rt△ABC中,∠C=90°
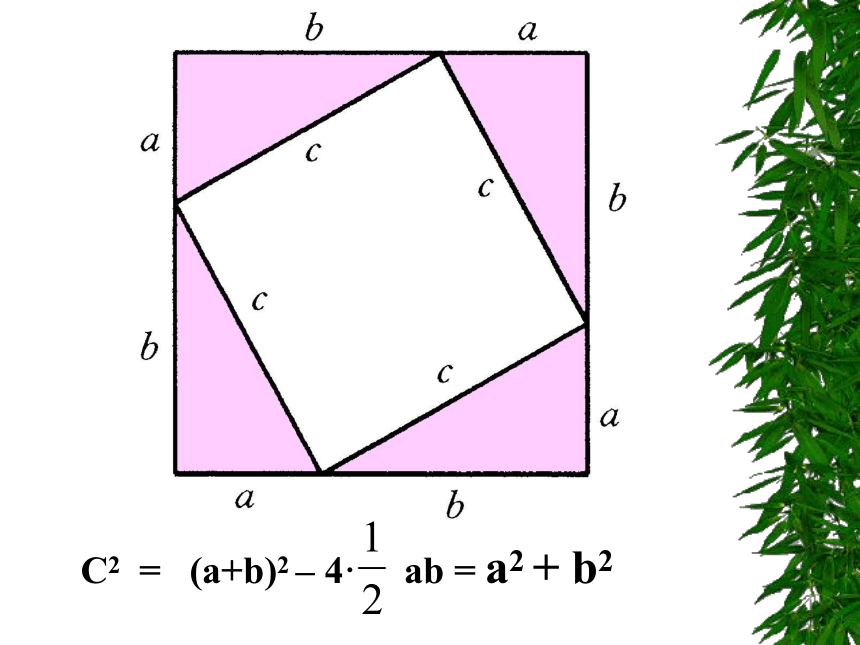
c2 = a2 + b2 C2 = (a+b)2 – 4· ab = a2 + b2例2 如图19.2.9,为了求出湖两岸的A、B两点之间
的距离,一个观测者在点C设桩,使三角形ABC恰
好为直角三角形.通过测量,得到AC长160米, BC长128米.问从点A穿过湖到点B有多远?
解:在Rt△ABC中,∠B=90°= 96(米)
答:从点A穿过湖到点B有96米.
?
1.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
2.假期中,王强和同学到某海岛上去探宝旅游,
按照探宝图(如图),他们登陆后先往东走8
千米,又往北走2千米,遇到障碍后又往西走3
千米,再折向北走到6千米处往东一拐,仅走1
千米就找到宝藏,问登陆点A到宝藏点B的直线
距离是多少千米?
C解:在Rt△ABC中,∠ACB=90°AC=6,BC=8AB ===10(千米)答:登陆点A到宝藏点B的直线
距离是10千米。
过点B作BC⊥AC于C d3d2d1S1=S2+S3
如果它的两条直角边分别为a、b,
斜边为c,那么一定有
a2+b2=c2
勾股定理 直角三角形两直角边的平方
和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
S梯形= (a+b)(a+b) = (a2+b2)+ abS梯形 = c2 +2 · ab = c2+ab 即:在Rt△ABC中,∠C=90°
c2 = a2 + b2 C2 = (a+b)2 – 4· ab = a2 + b2例2 如图19.2.9,为了求出湖两岸的A、B两点之间
的距离,一个观测者在点C设桩,使三角形ABC恰
好为直角三角形.通过测量,得到AC长160米, BC长128米.问从点A穿过湖到点B有多远?
解:在Rt△ABC中,∠B=90°= 96(米)
答:从点A穿过湖到点B有96米.
?
1.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
2.假期中,王强和同学到某海岛上去探宝旅游,
按照探宝图(如图),他们登陆后先往东走8
千米,又往北走2千米,遇到障碍后又往西走3
千米,再折向北走到6千米处往东一拐,仅走1
千米就找到宝藏,问登陆点A到宝藏点B的直线
距离是多少千米?
C解:在Rt△ABC中,∠ACB=90°AC=6,BC=8AB ===10(千米)答:登陆点A到宝藏点B的直线
距离是10千米。
过点B作BC⊥AC于C d3d2d1S1=S2+S3
