2023年中考数学复习讲义:第六章 勾股定理 (二十三)——赵爽弦图模型
文档属性
| 名称 | 2023年中考数学复习讲义:第六章 勾股定理 (二十三)——赵爽弦图模型 | 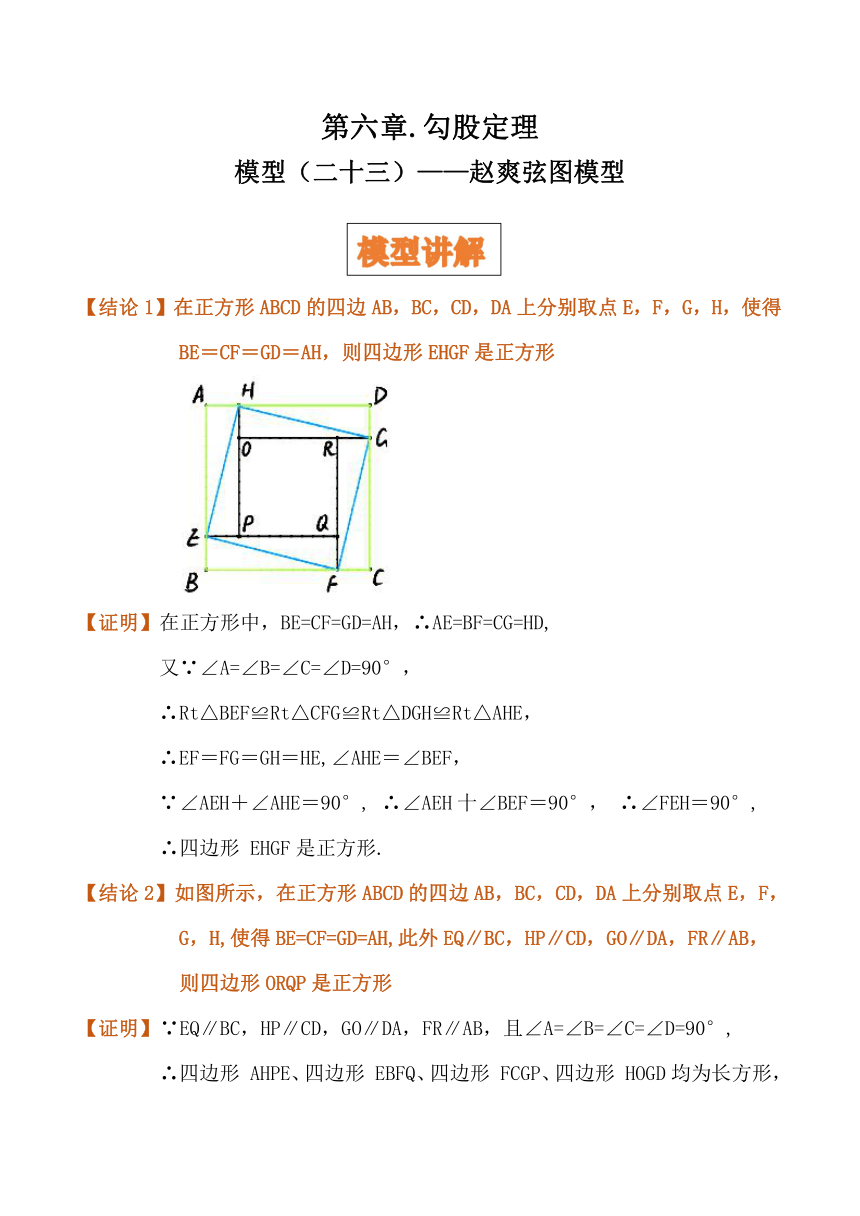 | |
| 格式 | docx | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 18:30:21 | ||
图片预览



文档简介
勾股定理
模型(二十三)——赵爽弦图模型
【结论1】在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,则四边形EHGF是正方形
【证明】在正方形中,BE=CF=GD=AH,∴AE=BF=CG=HD,
又∵∠A=∠B=∠C=∠D=90°,
∴Rt△BEF≌Rt△CFG≌Rt△DGH≌Rt△AHE,
∴EF=FG=GH=HE,∠AHE=∠BEF,
∵∠AEH+∠AHE=90°, ∴∠AEH十∠BEF=90°, ∴∠FEH=90°,
∴四边形 EHGF是正方形.
【结论2】如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,此外EQ∥BC,HP∥CD,GO∥DA,FR∥AB,
则四边形ORQP是正方形
【证明】∵EQ∥BC,HP∥CD,GO∥DA,FR∥AB,且∠A=∠B=∠C=∠D=90°,
∴四边形 AHPE、四边形 EBFQ、四边形 FCGP、四边形 HOGD均为长方形,
∴△AEH≌△PHE≌△BFE≌△QEF≌△CGF≌△RFG≌△DHG≌△OGH,
∴HP=EQ=FR=GO,EP=FQ=GR=HO,
∴OP=PQ=QR=RO,且∠ROP=180°-∠HOG=90°,
∴四边形 ORQP为正方形.
【结论3】如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,此外EQ∥BC,HP∥CD,GO∥DA,FR∥AB, 则(1)S正方形 =4S 十S正方形;
(2)S正方形 =4S十S正方形;
(3)S正方形-S正方形=S正方形-S正方形.
(4)2S正方形=S正方形十S正方形
如图,四个全等的直角三角形与一个小正方形镶嵌而成的图案,大正方形面积为49,小正方形面积为4,若x、y表示直角三角形的两直角边(x>y),则有:
⑴ x2+y2=49 勾股定理
⑵ x-y=2 小正方形边长=长直-短直
⑶ 2xy+4=49 面积算两次
常见的勾股数组合
①3,4,5; ②5,12,13;③6,8,10;④8,15,17;⑤9,12,15;
典例1 ☆☆☆☆☆
设直角三角形的较长直角边长为x,较短直角边长为y.若 x y=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
【答案】D
【解析】设小正方形的边长为 a(a>0),
∵ S大正方形=S小正形+4S直角三角形,S直角三角形=x·y,
∴ 25=a +×4×8,所以a=3.
故选 D.
典例2 ☆☆☆☆☆
如图,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
A.8 B.6 C.4 D.5
【答案】B
【解析】∵AB=10,EF=2,
∴大正方形的面积是100,小正方形的面积是4,
∴四个直角三角形的面积和为 100-4=96.
设 AE=a,DE=b,则4×ab=96,又a2+b2=100,
∴(a+b)2=a +b2+2ab=100+96=196,
∴a+b=14,又a-b=2,
∴a=8,b=6, ∴AH=DE=6. 故选 B.
典例3 ☆☆☆☆☆
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a,较短直角边为b,则 ab的值是( )
A.4 B.6 C.8 D.10
【答案】B
【解析】由模型结论可得四个直角三角形的面积是ab×4= 17-5=12,
即 ab= 6.故选 B.
1.(★★☆☆☆)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为 b,若(a+b)2= 21,大正方形的面积为 13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
2.(★★☆☆☆)“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是 3 和 7,则大正方形和小正方形的面积差是( ).
A.9 B.36 C.42 D.34
由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.
根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论∶若a>0,b>0且a2+b2为定值,则当a ____ b 时,ab取得最大值。
“赵爽弦图”的面积关系是中考常考的一种题型,一般出现在选择题、填空题中,如果能够记住面积之间的关系,那么做此类题时一定非常高效.
勾股定理
模型(二十三)——赵爽弦图模型
答案:
小试牛刀
答案 C
解析 ∵(a十b)2=21,∴a +2ab+b2= 21.∵大正方形的面积为13,
∴a +b2=13, ∴2ab=21-13=8,
∴小正方形的面积为 13-8=5.故选 C.
答案 C
解析 由题意得小正方形的面积为(7- 3)2=16,
大正方形的面积为32+7 =58,
∴大正方形和小正方形的面积之差为 58-16=42.
故选 C.
直击中考
1. 答案 =
解析 设 a2+b2为定值 k,则c =a2 +b2=k,由“赵爽弦图”可知,
2ab=c -(a-b)2=k-(a-b)2,即 ab=
要使ab的值最大,则需(a-b)2最小.
∵(a-b)2≥ 0,∴当a=b时,(a-b) 取得最小值,
故当 a=b时,ab 取得最大值.
模型(二十三)——赵爽弦图模型
【结论1】在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,则四边形EHGF是正方形
【证明】在正方形中,BE=CF=GD=AH,∴AE=BF=CG=HD,
又∵∠A=∠B=∠C=∠D=90°,
∴Rt△BEF≌Rt△CFG≌Rt△DGH≌Rt△AHE,
∴EF=FG=GH=HE,∠AHE=∠BEF,
∵∠AEH+∠AHE=90°, ∴∠AEH十∠BEF=90°, ∴∠FEH=90°,
∴四边形 EHGF是正方形.
【结论2】如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,此外EQ∥BC,HP∥CD,GO∥DA,FR∥AB,
则四边形ORQP是正方形
【证明】∵EQ∥BC,HP∥CD,GO∥DA,FR∥AB,且∠A=∠B=∠C=∠D=90°,
∴四边形 AHPE、四边形 EBFQ、四边形 FCGP、四边形 HOGD均为长方形,
∴△AEH≌△PHE≌△BFE≌△QEF≌△CGF≌△RFG≌△DHG≌△OGH,
∴HP=EQ=FR=GO,EP=FQ=GR=HO,
∴OP=PQ=QR=RO,且∠ROP=180°-∠HOG=90°,
∴四边形 ORQP为正方形.
【结论3】如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,F,G,H,使得BE=CF=GD=AH,此外EQ∥BC,HP∥CD,GO∥DA,FR∥AB, 则(1)S正方形 =4S 十S正方形;
(2)S正方形 =4S十S正方形;
(3)S正方形-S正方形=S正方形-S正方形.
(4)2S正方形=S正方形十S正方形
如图,四个全等的直角三角形与一个小正方形镶嵌而成的图案,大正方形面积为49,小正方形面积为4,若x、y表示直角三角形的两直角边(x>y),则有:
⑴ x2+y2=49 勾股定理
⑵ x-y=2 小正方形边长=长直-短直
⑶ 2xy+4=49 面积算两次
常见的勾股数组合
①3,4,5; ②5,12,13;③6,8,10;④8,15,17;⑤9,12,15;
典例1 ☆☆☆☆☆
设直角三角形的较长直角边长为x,较短直角边长为y.若 x y=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
【答案】D
【解析】设小正方形的边长为 a(a>0),
∵ S大正方形=S小正形+4S直角三角形,S直角三角形=x·y,
∴ 25=a +×4×8,所以a=3.
故选 D.
典例2 ☆☆☆☆☆
如图,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
A.8 B.6 C.4 D.5
【答案】B
【解析】∵AB=10,EF=2,
∴大正方形的面积是100,小正方形的面积是4,
∴四个直角三角形的面积和为 100-4=96.
设 AE=a,DE=b,则4×ab=96,又a2+b2=100,
∴(a+b)2=a +b2+2ab=100+96=196,
∴a+b=14,又a-b=2,
∴a=8,b=6, ∴AH=DE=6. 故选 B.
典例3 ☆☆☆☆☆
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a,较短直角边为b,则 ab的值是( )
A.4 B.6 C.8 D.10
【答案】B
【解析】由模型结论可得四个直角三角形的面积是ab×4= 17-5=12,
即 ab= 6.故选 B.
1.(★★☆☆☆)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为 b,若(a+b)2= 21,大正方形的面积为 13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
2.(★★☆☆☆)“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是 3 和 7,则大正方形和小正方形的面积差是( ).
A.9 B.36 C.42 D.34
由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.
根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论∶若a>0,b>0且a2+b2为定值,则当a ____ b 时,ab取得最大值。
“赵爽弦图”的面积关系是中考常考的一种题型,一般出现在选择题、填空题中,如果能够记住面积之间的关系,那么做此类题时一定非常高效.
勾股定理
模型(二十三)——赵爽弦图模型
答案:
小试牛刀
答案 C
解析 ∵(a十b)2=21,∴a +2ab+b2= 21.∵大正方形的面积为13,
∴a +b2=13, ∴2ab=21-13=8,
∴小正方形的面积为 13-8=5.故选 C.
答案 C
解析 由题意得小正方形的面积为(7- 3)2=16,
大正方形的面积为32+7 =58,
∴大正方形和小正方形的面积之差为 58-16=42.
故选 C.
直击中考
1. 答案 =
解析 设 a2+b2为定值 k,则c =a2 +b2=k,由“赵爽弦图”可知,
2ab=c -(a-b)2=k-(a-b)2,即 ab=
要使ab的值最大,则需(a-b)2最小.
∵(a-b)2≥ 0,∴当a=b时,(a-b) 取得最小值,
故当 a=b时,ab 取得最大值.
同课章节目录
