2023年中考数学复习讲义:第三章 三角形 模型(七)——飞镖模型
文档属性
| 名称 | 2023年中考数学复习讲义:第三章 三角形 模型(七)——飞镖模型 |
|
|
| 格式 | doc | ||
| 文件大小 | 776.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 18:31:27 | ||
图片预览


文档简介
三角形
模型(七)——飞镖模型
【结论】如图所示,已知四边形ABDC,则∠BDC=∠A+∠B+∠C
【证明】如图,延长 BD交 AC 于点E.
∵∠BEC是△ABE 的外角, ∴∠BEC=∠A+∠B.
又∵∠BDC 是△CDE的外角,
∴∠BDC=∠BEC+∠C=∠A+∠B+∠C.
其他添加轴助线的方法
典例1 ☆☆☆☆☆
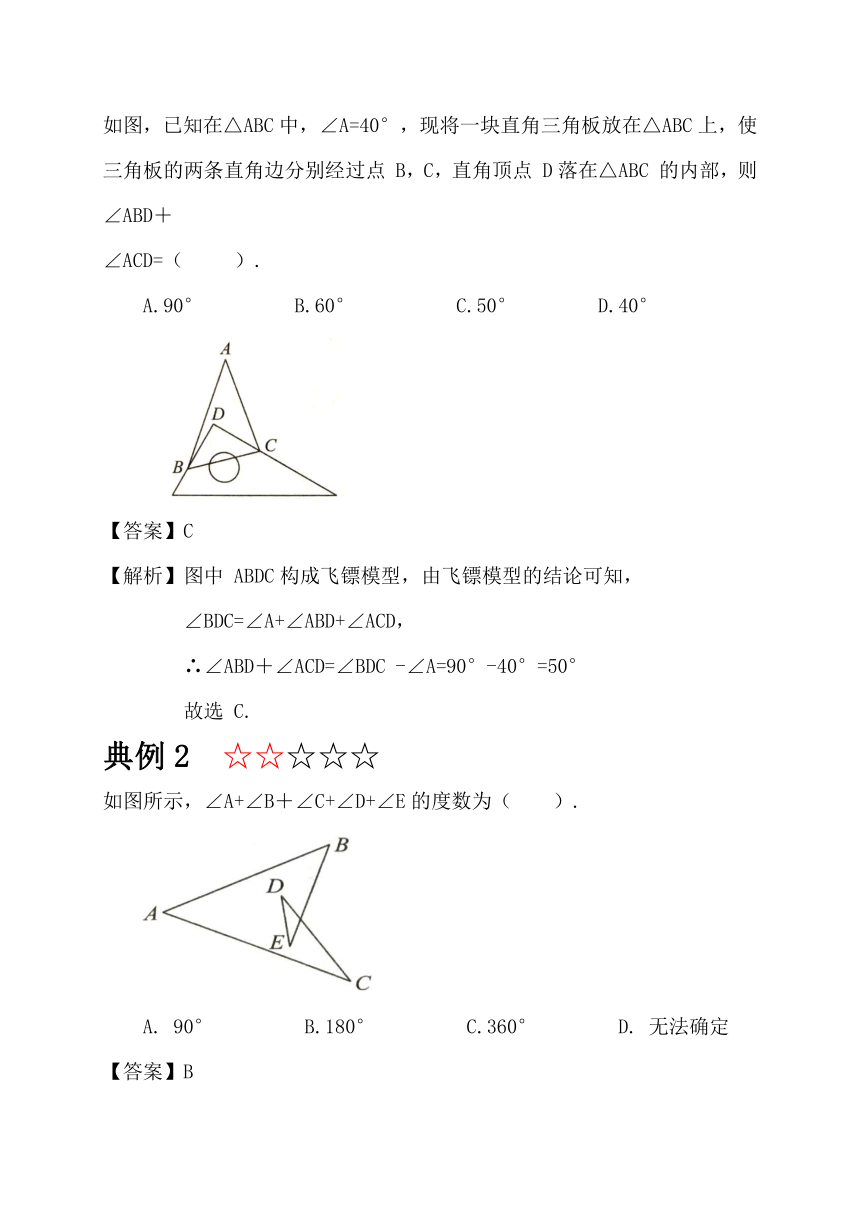
如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点 B,C,直角顶点 D落在△ABC 的内部,则∠ABD+
∠ACD=( ).
A.90° B.60° C.50° D.40°
【答案】C
【解析】图中 ABDC构成飞镖模型,由飞镖模型的结论可知,
∠BDC=∠A+∠ABD+∠ACD,
∴∠ABD+∠ACD=∠BDC -∠A=90°-40°=50°
故选 C.
典例2 ☆☆☆☆☆
如图所示,∠A+∠B+∠C+∠D+∠E的度数为( ).
A. 90° B.180° C.360° D. 无法确定
【答案】B
【解析】如图,此图满足飞镖模型,由飞镖模型的结论得,
∠BPC=∠A+∠B+∠C.
∵∠BPC=∠DPE,
∴∠A+∠B+∠C+∠D+∠E=∠DPE+∠D+∠E=180°.故选 B.
典例3 ☆☆☆☆☆
在社会实践手工课上,狗蛋同学设计了一个形状如图所示的零件,如果∠A=52°,∠B=25°,∠C=30°,∠D=35°,∠E=72°,那么∠F的度数是( )
A.72° B.70° C.65° D.60°
【答案】B
【解析】如图,连接 AD,此时图形转化为两个飞镖模型.
由飞镖模型的结论,得∠E=∠B+∠ADE﹢∠BAD,∠F= ∠ADF+∠C+∠DAC,
∴∠E+∠F =(∠B+∠ADE+∠BAD)+(∠CAD+∠ADF+∠C)
= ∠B+∠C+(∠BAD + ∠CAD)+(∠ADE+∠ADF)
=∠B+∠C+∠BAC+∠EDF=142°.
∴∠F=142°-∠E=142°-72°=70°,故选 B.
1.(★★☆☆☆)如图,∠BDC=98°,∠C=38°,∠A=37°,则∠B的度数是( )
A.33° B.23° C.27° D.37
(第 1 题图) (第 2 题图)
2.(★★☆☆☆)如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
3.(★★☆☆☆)如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=_______。
如图,已知 BE,CF分别为△ABC的两条高,BE 和CF 相交于点 H.若
∠BAC=50°,则∠BHC为( ).
A.115° B.120° C.125° D.130°
在中考考试中 ,飞镖模型主要以选择题或填空题的形式出现 .同时 ,在几何解答题中 ,利用飞镖模型也能帮我们快速找到角之间的关系,对提高解题速度有很大的帮助 .
第三章.三角形
模型(七)——飞镖模型
答案:
小试牛刀
答案 B
解析 :由飞镖模型的结论可得,∠BDC= ∠A+∠B+∠C,
∴∠B=∠BDC -∠A-∠C =98 -37 -38 =23
故选B.
答案 C
解析 : 由飞镖模型的结论可得 ,∠AFB=∠A+∠B+∠C,
∴∠DFE=∠AFB =27 +45 +38 =110 ,
故选C.
3.答案 230
解析:由飞镖模型的结论可得 ,∠BOF=∠A+∠B+∠F,∠COE=∠C+∠D+∠E,
又∵∠EOC=115 , 且 ∠BOF=∠COE,
∴∠A+∠B+∠C +∠D+∠E+∠F=∠BOF+∠COE =115 +115 =230
直击中考
1. 答案 D
解析: 由飞镖模型的结论可得 ,∠BHC=∠A+∠ABH+∠HCA
∵BE,CF分别为△ABC的两条高,∠BAC=50 ,
∴∠ABH=∠HCA=90 -∠BAC=90 -50 =40 ,
∴∠BHC=50 +40 +40 =130 ,故选D.
模型讲解
典例秒杀
小试牛刀
直击中考
模型(七)——飞镖模型
【结论】如图所示,已知四边形ABDC,则∠BDC=∠A+∠B+∠C
【证明】如图,延长 BD交 AC 于点E.
∵∠BEC是△ABE 的外角, ∴∠BEC=∠A+∠B.
又∵∠BDC 是△CDE的外角,
∴∠BDC=∠BEC+∠C=∠A+∠B+∠C.
其他添加轴助线的方法
典例1 ☆☆☆☆☆
如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点 B,C,直角顶点 D落在△ABC 的内部,则∠ABD+
∠ACD=( ).
A.90° B.60° C.50° D.40°
【答案】C
【解析】图中 ABDC构成飞镖模型,由飞镖模型的结论可知,
∠BDC=∠A+∠ABD+∠ACD,
∴∠ABD+∠ACD=∠BDC -∠A=90°-40°=50°
故选 C.
典例2 ☆☆☆☆☆
如图所示,∠A+∠B+∠C+∠D+∠E的度数为( ).
A. 90° B.180° C.360° D. 无法确定
【答案】B
【解析】如图,此图满足飞镖模型,由飞镖模型的结论得,
∠BPC=∠A+∠B+∠C.
∵∠BPC=∠DPE,
∴∠A+∠B+∠C+∠D+∠E=∠DPE+∠D+∠E=180°.故选 B.
典例3 ☆☆☆☆☆
在社会实践手工课上,狗蛋同学设计了一个形状如图所示的零件,如果∠A=52°,∠B=25°,∠C=30°,∠D=35°,∠E=72°,那么∠F的度数是( )
A.72° B.70° C.65° D.60°
【答案】B
【解析】如图,连接 AD,此时图形转化为两个飞镖模型.
由飞镖模型的结论,得∠E=∠B+∠ADE﹢∠BAD,∠F= ∠ADF+∠C+∠DAC,
∴∠E+∠F =(∠B+∠ADE+∠BAD)+(∠CAD+∠ADF+∠C)
= ∠B+∠C+(∠BAD + ∠CAD)+(∠ADE+∠ADF)
=∠B+∠C+∠BAC+∠EDF=142°.
∴∠F=142°-∠E=142°-72°=70°,故选 B.
1.(★★☆☆☆)如图,∠BDC=98°,∠C=38°,∠A=37°,则∠B的度数是( )
A.33° B.23° C.27° D.37
(第 1 题图) (第 2 题图)
2.(★★☆☆☆)如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
3.(★★☆☆☆)如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=_______。
如图,已知 BE,CF分别为△ABC的两条高,BE 和CF 相交于点 H.若
∠BAC=50°,则∠BHC为( ).
A.115° B.120° C.125° D.130°
在中考考试中 ,飞镖模型主要以选择题或填空题的形式出现 .同时 ,在几何解答题中 ,利用飞镖模型也能帮我们快速找到角之间的关系,对提高解题速度有很大的帮助 .
第三章.三角形
模型(七)——飞镖模型
答案:
小试牛刀
答案 B
解析 :由飞镖模型的结论可得,∠BDC= ∠A+∠B+∠C,
∴∠B=∠BDC -∠A-∠C =98 -37 -38 =23
故选B.
答案 C
解析 : 由飞镖模型的结论可得 ,∠AFB=∠A+∠B+∠C,
∴∠DFE=∠AFB =27 +45 +38 =110 ,
故选C.
3.答案 230
解析:由飞镖模型的结论可得 ,∠BOF=∠A+∠B+∠F,∠COE=∠C+∠D+∠E,
又∵∠EOC=115 , 且 ∠BOF=∠COE,
∴∠A+∠B+∠C +∠D+∠E+∠F=∠BOF+∠COE =115 +115 =230
直击中考
1. 答案 D
解析: 由飞镖模型的结论可得 ,∠BHC=∠A+∠ABH+∠HCA
∵BE,CF分别为△ABC的两条高,∠BAC=50 ,
∴∠ABH=∠HCA=90 -∠BAC=90 -50 =40 ,
∴∠BHC=50 +40 +40 =130 ,故选D.
模型讲解
典例秒杀
小试牛刀
直击中考
同课章节目录
