2023年中考数学复习讲义:第二章 相交线与平行线 模型(三)——猪蹄模型
文档属性
| 名称 | 2023年中考数学复习讲义:第二章 相交线与平行线 模型(三)——猪蹄模型 |
|
|
| 格式 | doc | ||
| 文件大小 | 677.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 00:00:00 | ||
图片预览



文档简介
第二章.相交线与平行线
模型(三)——猪蹄模型
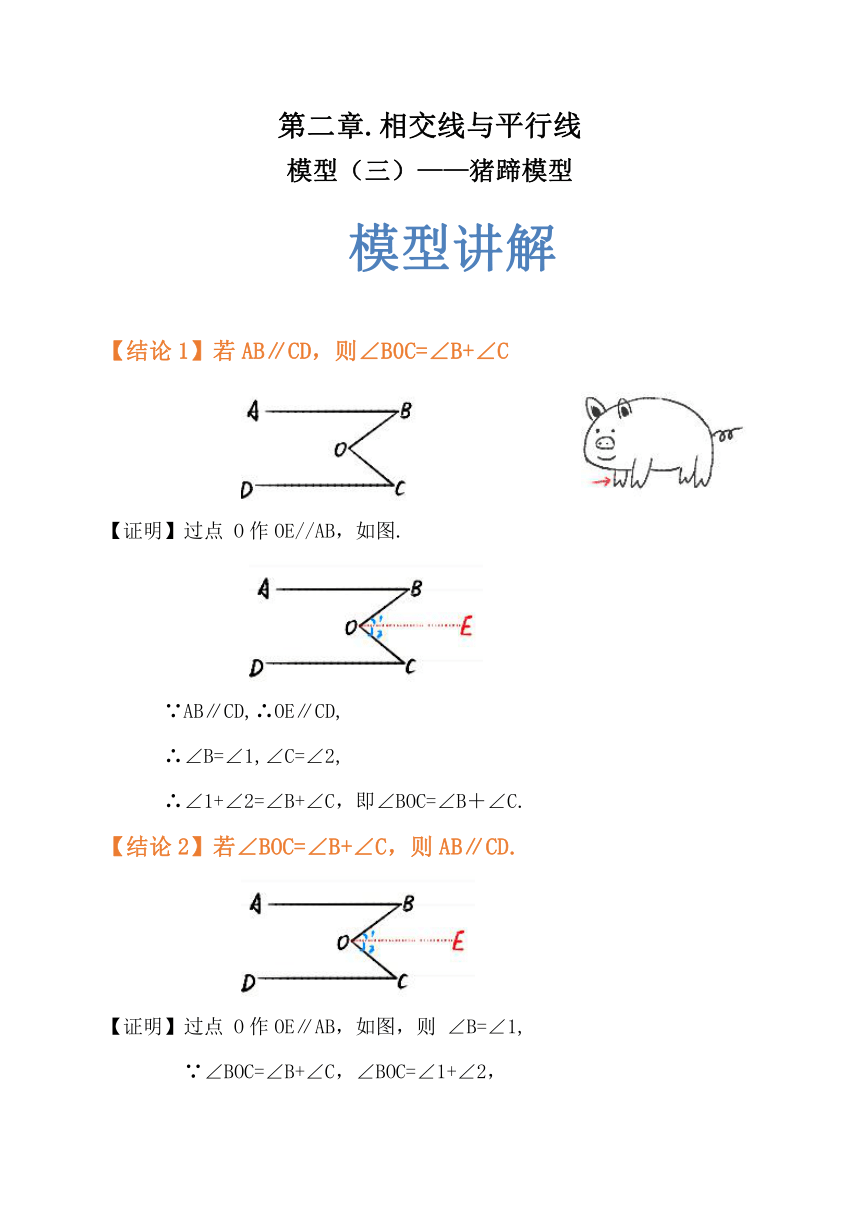
【结论1】若AB∥CD,则∠B0C=∠B+∠C
【证明】过点 O作OE//AB,如图.
∵AB∥CD,∴OE∥CD,
∴∠B=∠1,∠C=∠2,
∴∠1+∠2=∠B+∠C,即∠BOC=∠B+∠C.
【结论2】若∠BOC=∠B+∠C,则AB∥CD.
【证明】过点 O作OE∥AB,如图,则 ∠B=∠1,
∵∠BOC=∠B+∠C,∠BOC=∠1+∠2,
∴∠1+∠2=∠B+∠C,∴∠C=∠2,∴OE∥DC,
又OE∥AB,∴AB∥CD.
典例1 ☆☆☆☆☆
如图,∠BCD=90°,AB// DE,则∠α与∠β一定满足的等式是( )
A.∠α+∠β= 180° B. ∠α+∠β= 90°
C.∠β=3∠α D.∠α -∠β=90°
【答案】D
【解析】如图所示,这里隐藏了一个猪蹄模型.
根据猪蹄模型的结论,可知∠1+∠β= ∠BCD=90°.
又∠1+∠α=180°, ∴∠1+∠β=180°-∠α+∠β=90°,
∴∠α -∠β= 90°.故选 D.
典例2 ☆☆☆☆☆
如图,狗蛋在美术课上用丝线绣成了一个“2”,AB∥DE,∠A=30°,∠ACE=110°,则∠E的度数为( )
A.30° B.150° C.120° D.100°
【答案】 D
【解析】如图,过点E作DE的延长线EF.
∵AB∥DF,
∴FECAB 构成猪蹄模型.
根据猪蹄模型的结论,可知∠FEC+∠CAB=∠ACE,
∴∠FEC=∠ACE-∠CAB=110°-30°=80°.
∵∠FEC+∠DEC=180°,
∴∠DEC=180°-∠FEC=180°-80°=100°.故选 D.
1.(★★☆☆☆)把一副三角板放在水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1 的度数是( ).
A.90° B.105° C. 120° D.135°
2.(★★☆☆☆)如图,已知 AB//CD,∠1=50°,∠2=113°,则∠3=_____°。
1.如图,已知 AB//DE,∠1=30°,∠2=35°,则∠BCE 的度数为( )
A.70° B. 65° C.35° D.5°
2.如图,直线 l //l ,∠1=30°,则∠2十∠3= ( )
A.150° B. 180° C.210° D.240°
第二章.相交线与平行线
模型(3)——猪蹄模型
答案:
小试牛刀
答案 B
解析 :如图,BAOCD构成了猪蹄模型
根据猪蹄模型结论可得∠A+∠C=∠1
∵∠A=60°,∠C=450°,
∴∠1=60°+45°=105°,故选B。
答案 63
解析:∵AB∥CD, ∴BAOCD构成了猪蹄模型,
∴∠1+∠3=∠2
∴∠3=∠2-∠1=113°-50°=63°
直击中考
答案 B
解析 :∵AB∥CD,∴A B C E D构成了猪蹄模型,
∴∠1+∠2=∠BCE
∴∠BCE=30°+35°=65°.
故选 B
2. 答案 C
解析 如图,∵l ∥l ,
∴这里隐藏了一个猪蹄模型,∴ ∠1+∠4=∠2.
∵∠4+∠3=180°,∴∠4=180°-∠3,
∴∠1+∠4=∠1+180°-∠3=∠2,
∴∠2+∠3= ∠1+180°= 30°+180°= 210°.故选 C.
模型讲解
典型秒杀
小试牛刀
直击中考
模型(三)——猪蹄模型
【结论1】若AB∥CD,则∠B0C=∠B+∠C
【证明】过点 O作OE//AB,如图.
∵AB∥CD,∴OE∥CD,
∴∠B=∠1,∠C=∠2,
∴∠1+∠2=∠B+∠C,即∠BOC=∠B+∠C.
【结论2】若∠BOC=∠B+∠C,则AB∥CD.
【证明】过点 O作OE∥AB,如图,则 ∠B=∠1,
∵∠BOC=∠B+∠C,∠BOC=∠1+∠2,
∴∠1+∠2=∠B+∠C,∴∠C=∠2,∴OE∥DC,
又OE∥AB,∴AB∥CD.
典例1 ☆☆☆☆☆
如图,∠BCD=90°,AB// DE,则∠α与∠β一定满足的等式是( )
A.∠α+∠β= 180° B. ∠α+∠β= 90°
C.∠β=3∠α D.∠α -∠β=90°
【答案】D
【解析】如图所示,这里隐藏了一个猪蹄模型.
根据猪蹄模型的结论,可知∠1+∠β= ∠BCD=90°.
又∠1+∠α=180°, ∴∠1+∠β=180°-∠α+∠β=90°,
∴∠α -∠β= 90°.故选 D.
典例2 ☆☆☆☆☆
如图,狗蛋在美术课上用丝线绣成了一个“2”,AB∥DE,∠A=30°,∠ACE=110°,则∠E的度数为( )
A.30° B.150° C.120° D.100°
【答案】 D
【解析】如图,过点E作DE的延长线EF.
∵AB∥DF,
∴FECAB 构成猪蹄模型.
根据猪蹄模型的结论,可知∠FEC+∠CAB=∠ACE,
∴∠FEC=∠ACE-∠CAB=110°-30°=80°.
∵∠FEC+∠DEC=180°,
∴∠DEC=180°-∠FEC=180°-80°=100°.故选 D.
1.(★★☆☆☆)把一副三角板放在水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1 的度数是( ).
A.90° B.105° C. 120° D.135°
2.(★★☆☆☆)如图,已知 AB//CD,∠1=50°,∠2=113°,则∠3=_____°。
1.如图,已知 AB//DE,∠1=30°,∠2=35°,则∠BCE 的度数为( )
A.70° B. 65° C.35° D.5°
2.如图,直线 l //l ,∠1=30°,则∠2十∠3= ( )
A.150° B. 180° C.210° D.240°
第二章.相交线与平行线
模型(3)——猪蹄模型
答案:
小试牛刀
答案 B
解析 :如图,BAOCD构成了猪蹄模型
根据猪蹄模型结论可得∠A+∠C=∠1
∵∠A=60°,∠C=450°,
∴∠1=60°+45°=105°,故选B。
答案 63
解析:∵AB∥CD, ∴BAOCD构成了猪蹄模型,
∴∠1+∠3=∠2
∴∠3=∠2-∠1=113°-50°=63°
直击中考
答案 B
解析 :∵AB∥CD,∴A B C E D构成了猪蹄模型,
∴∠1+∠2=∠BCE
∴∠BCE=30°+35°=65°.
故选 B
2. 答案 C
解析 如图,∵l ∥l ,
∴这里隐藏了一个猪蹄模型,∴ ∠1+∠4=∠2.
∵∠4+∠3=180°,∴∠4=180°-∠3,
∴∠1+∠4=∠1+180°-∠3=∠2,
∴∠2+∠3= ∠1+180°= 30°+180°= 210°.故选 C.
模型讲解
典型秒杀
小试牛刀
直击中考
同课章节目录
