第七章 平面直角坐标系 单元练习(含答案)2022—2023学年人教版数学七年级下册
文档属性
| 名称 | 第七章 平面直角坐标系 单元练习(含答案)2022—2023学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 564.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 20:21:18 | ||
图片预览


文档简介
第七章 平面直角坐标系 单元练习
一、单选题
1.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
2.若点在第三象限,且点到轴的距离为,到轴的距离为,则点的坐标是( )
A. B. C. D.
3.在平面直角坐标系中,将点先向右平移4个长度单位,再向下平移5个长度单位得到点B,则点B的坐标是( )
A. B. C. D.
4.根据下列表述,能确定具体位置的是( )
A.某电影院2排 B.大桥南路 C.北偏东30° D.东经108°,北纬43°
5.平行于x轴的直线上的点的纵坐标一定( )
A.大于0 B.小于0 C.互为相反数 D.相等
6.如图,动点P从出发,沿箭头所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时,点P的坐标为( )
A. B. C. D.
7.已知点M(﹣2,3),线段MN=3,且MN∥y轴,则点N的坐标是( )
A.(﹣2,0) B.(1,3)
C.(1,3)或(﹣5,3) D.(﹣2,0)或(﹣2,6)
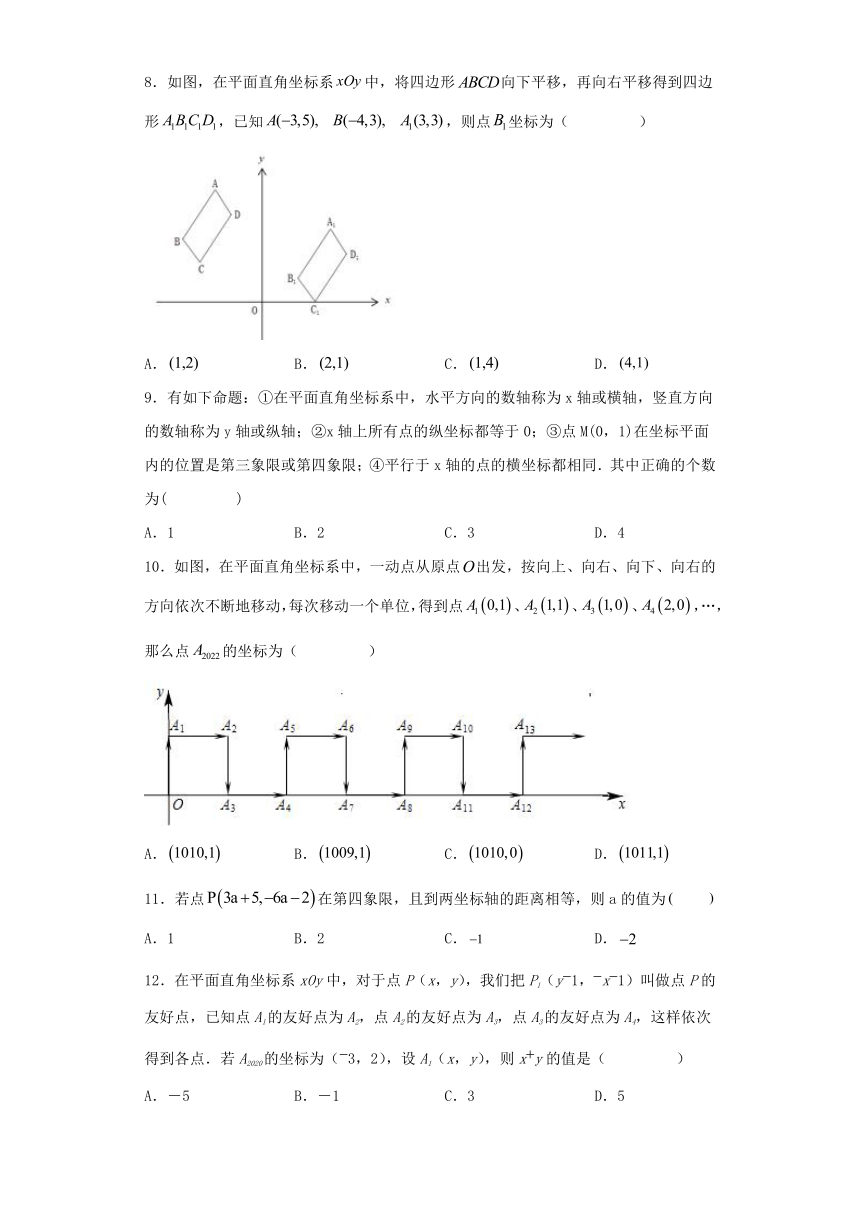
8.如图,在平面直角坐标系中,将四边形向下平移,再向右平移得到四边形,已知,则点坐标为( )
A. B. C. D.
9.有如下命题:①在平面直角坐标系中,水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴;②x轴上所有点的纵坐标都等于0;③点M(0,1)在坐标平面内的位置是第三象限或第四象限;④平行于x轴的点的横坐标都相同.其中正确的个数为( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点、、、,…,那么点的坐标为( )
A. B. C. D.
11.若点在第四象限,且到两坐标轴的距离相等,则a的值为
A.1 B.2 C. D.
12.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y1,x1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2020的坐标为(3,2),设A1(x,y),则xy的值是( )
A.-5 B.-1 C.3 D.5
二、填空题
13.若点(m-5,1-2m)在第三象限内,则m的取值范围是__________
14.已知点A的坐标为(﹣2,0),点B的坐标为(0 ,3),点C在坐标轴上,且三角形ABC的面积是3,则点C的坐标为_______________.
15.如图,在平面直角坐标系中,,,,则C的坐标为__________.
16.定义:直线l1与l2相交于点O,对于平面内任意一点P,点P到直线l1与l2的距离分别为p、q,则称有序实数对(p,q)是点P的“距离坐标”,根据上述定义,“距离坐标”是(3,2)的点的个数有______个.
17.如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是_____________.
18.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是________.
三、解答题
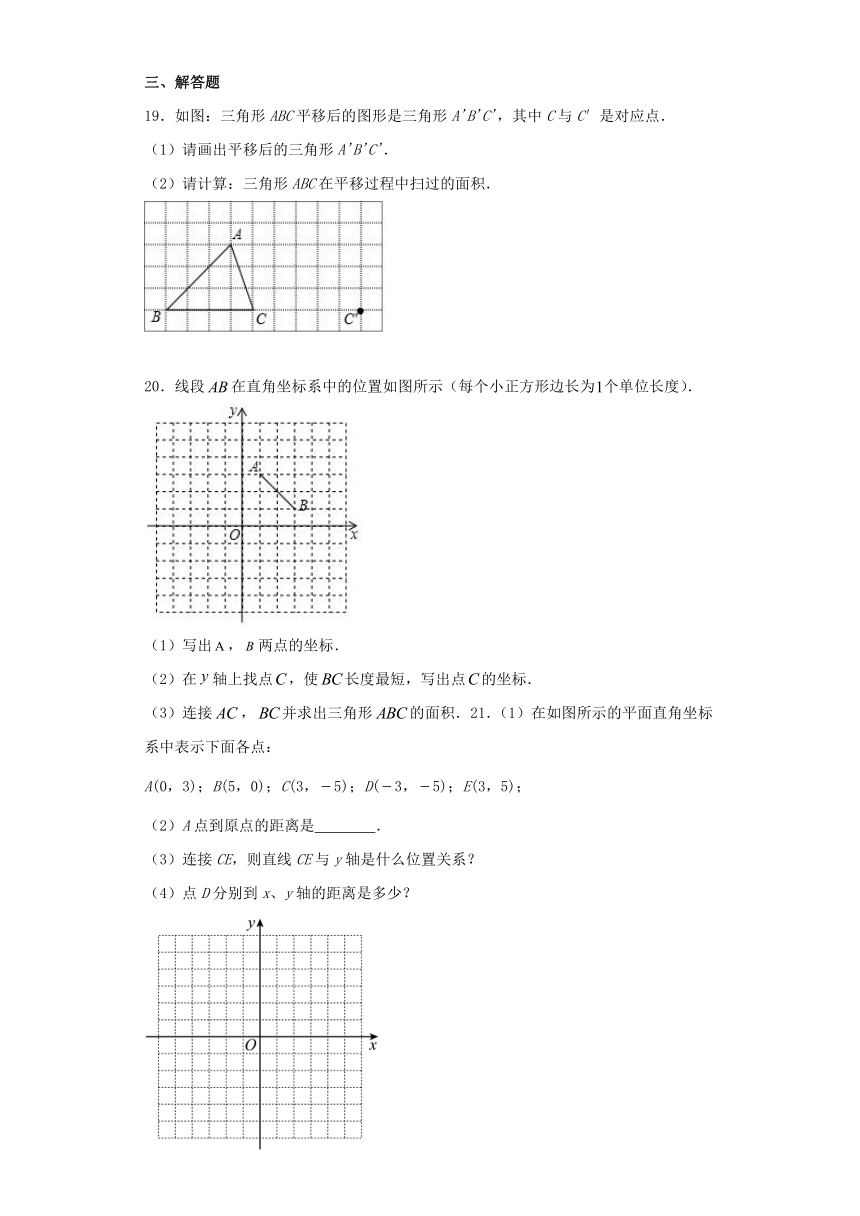
19.如图:三角形ABC平移后的图形是三角形A'B'C',其中C与C′是对应点.
(1)请画出平移后的三角形A'B'C'.
(2)请计算:三角形ABC在平移过程中扫过的面积.
20.线段在直角坐标系中的位置如图所示(每个小正方形边长为个单位长度).
(1)写出,两点的坐标.
(2)在轴上找点,使长度最短,写出点的坐标.
(3)连接,并求出三角形的面积.21.(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3, 5);D( 3, 5);E(3,5);
(2)A点到原点的距离是 .
(3)连接CE,则直线CE与y轴是什么位置关系?
(4)点D分别到x、y轴的距离是多少?
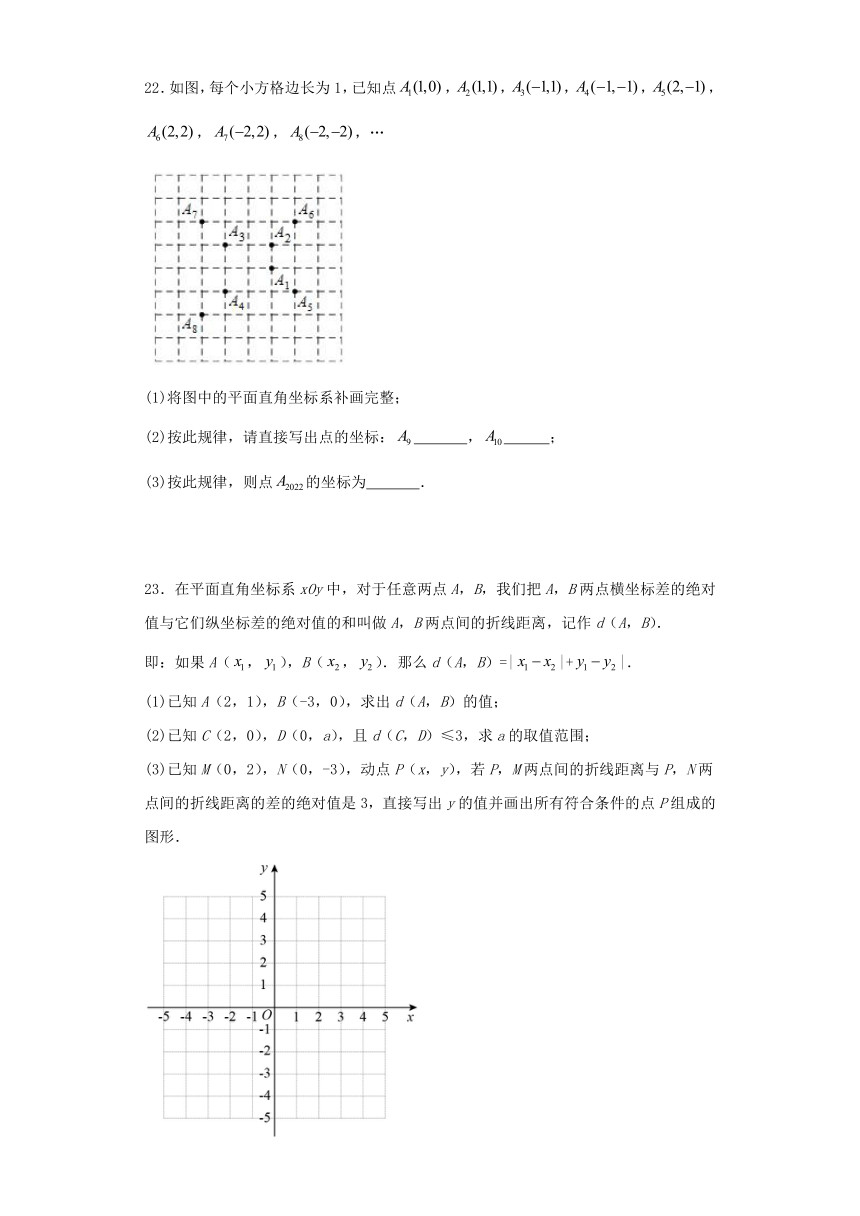
22.如图,每个小方格边长为1,已知点,,,,,,,,…
(1)将图中的平面直角坐标系补画完整;
(2)按此规律,请直接写出点的坐标: , ;
(3)按此规律,则点的坐标为 .
23.在平面直角坐标系xOy中,对于任意两点A,B,我们把A,B两点横坐标差的绝对值与它们纵坐标差的绝对值的和叫做A,B两点间的折线距离,记作d(A,B).
即:如果A(,),B(,).那么d(A,B)=||+|.
(1)已知A(2,1),B(-3,0),求出d(A,B)的值;
(2)已知C(2,0),D(0,a),且d(C,D)≤3,求a的取值范围;
(3)已知M(0,2),N(0,-3),动点P(x,y),若P,M两点间的折线距离与P,N两点间的折线距离的差的绝对值是3,直接写出y的值并画出所有符合条件的点P组成的图形.
24.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
参考答案
1.D
2.A
3.C
4.D
5.D
6.A
7.D
8.B
9.B
10.D
11.A
12.C
13.
14.(0,0)或(0,6)或(﹣4,0).
15.(10,0)
16.4个
17.4≤m≤8
18.(1,3)
19.(1)如图所示见解析;(2)21.
【详解】解:(1)如图所示:△A′B′C′即为平移后的三角形.
(2)△ABC在平移过程中扫过的面积=5×3+ ×4×3=15+6=21.
故答案为(1)如图所示见解析;(2)21.
20.(1),;(2);(3) 3
【详解】解:(1),;
(2)∵点到直线上一点的距离,垂线段最短
∴;
(3)如图所示:,就是所求的线段
三角形的面积:.
21.(1)见解析;(2)3;(3)平行;(4)点D到x轴的距离是5,点D到y轴的距离是3.
【详解】解:(1)如图:
;
(2)A点到原点的距离是3,
故答案为:3;
(3)∵CE的横坐标都是3,
∴直线CE与y轴平行;
(4)点D到x轴的距离是5,点D到y轴的距离是3.
22.(1)见解析
(2),
(3)
【详解】(1)解:根据题意补画得平面直角坐标系如图所示:
(2)根据图示坐标系各象限横纵坐标符号特点可得:A9(3,-2),A10(3,3);
(3)观察图形发现,下标为4n+2的点落在第一象限的对角线上,
∵A2(1,1), A6(2,2),
∴A4n+2(n+1,n+1),
∵2022=4×505+2,
∴A2022(506,506),
故答案为:(506,506).
23.(1)6
(2)
(3)1或-2,图见解析
【详解】(1)解:由题意可知:d(A,B)=|2-(-3)|+|1-0|=5+1=6;
(2)解:∵d(C,D)=2+|a|≤3,
∴|a|≤1,
∴-1≤a≤1;
(3)解:d(P,M)=|x|+|y-2|,d(P,N)=|x|+|y+3|,
由题意可知:||y-2|-|y+3||=3,
当y<-3时,
等式的左边=5,此时不满足题意;
当-3<y<2时,
等式的左边=|2y+1|,
即|2y+1|=3,
解得:y=1或y=-2,
当y>2时,
等式的左边=5,不符合题意,
综上所述,点P(x,1)或(x,-2),
如图所示.
.
24.见解析
试题解析:(1)三角形向下平移7个单位得到三角形
(2)三角形向右平移6个单位,再向下平移3个单位得三角形
一、单选题
1.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
2.若点在第三象限,且点到轴的距离为,到轴的距离为,则点的坐标是( )
A. B. C. D.
3.在平面直角坐标系中,将点先向右平移4个长度单位,再向下平移5个长度单位得到点B,则点B的坐标是( )
A. B. C. D.
4.根据下列表述,能确定具体位置的是( )
A.某电影院2排 B.大桥南路 C.北偏东30° D.东经108°,北纬43°
5.平行于x轴的直线上的点的纵坐标一定( )
A.大于0 B.小于0 C.互为相反数 D.相等
6.如图,动点P从出发,沿箭头所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时,点P的坐标为( )
A. B. C. D.
7.已知点M(﹣2,3),线段MN=3,且MN∥y轴,则点N的坐标是( )
A.(﹣2,0) B.(1,3)
C.(1,3)或(﹣5,3) D.(﹣2,0)或(﹣2,6)
8.如图,在平面直角坐标系中,将四边形向下平移,再向右平移得到四边形,已知,则点坐标为( )
A. B. C. D.
9.有如下命题:①在平面直角坐标系中,水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴;②x轴上所有点的纵坐标都等于0;③点M(0,1)在坐标平面内的位置是第三象限或第四象限;④平行于x轴的点的横坐标都相同.其中正确的个数为( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点、、、,…,那么点的坐标为( )
A. B. C. D.
11.若点在第四象限,且到两坐标轴的距离相等,则a的值为
A.1 B.2 C. D.
12.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y1,x1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2020的坐标为(3,2),设A1(x,y),则xy的值是( )
A.-5 B.-1 C.3 D.5
二、填空题
13.若点(m-5,1-2m)在第三象限内,则m的取值范围是__________
14.已知点A的坐标为(﹣2,0),点B的坐标为(0 ,3),点C在坐标轴上,且三角形ABC的面积是3,则点C的坐标为_______________.
15.如图,在平面直角坐标系中,,,,则C的坐标为__________.
16.定义:直线l1与l2相交于点O,对于平面内任意一点P,点P到直线l1与l2的距离分别为p、q,则称有序实数对(p,q)是点P的“距离坐标”,根据上述定义,“距离坐标”是(3,2)的点的个数有______个.
17.如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是_____________.
18.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是________.
三、解答题
19.如图:三角形ABC平移后的图形是三角形A'B'C',其中C与C′是对应点.
(1)请画出平移后的三角形A'B'C'.
(2)请计算:三角形ABC在平移过程中扫过的面积.
20.线段在直角坐标系中的位置如图所示(每个小正方形边长为个单位长度).
(1)写出,两点的坐标.
(2)在轴上找点,使长度最短,写出点的坐标.
(3)连接,并求出三角形的面积.21.(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3, 5);D( 3, 5);E(3,5);
(2)A点到原点的距离是 .
(3)连接CE,则直线CE与y轴是什么位置关系?
(4)点D分别到x、y轴的距离是多少?
22.如图,每个小方格边长为1,已知点,,,,,,,,…
(1)将图中的平面直角坐标系补画完整;
(2)按此规律,请直接写出点的坐标: , ;
(3)按此规律,则点的坐标为 .
23.在平面直角坐标系xOy中,对于任意两点A,B,我们把A,B两点横坐标差的绝对值与它们纵坐标差的绝对值的和叫做A,B两点间的折线距离,记作d(A,B).
即:如果A(,),B(,).那么d(A,B)=||+|.
(1)已知A(2,1),B(-3,0),求出d(A,B)的值;
(2)已知C(2,0),D(0,a),且d(C,D)≤3,求a的取值范围;
(3)已知M(0,2),N(0,-3),动点P(x,y),若P,M两点间的折线距离与P,N两点间的折线距离的差的绝对值是3,直接写出y的值并画出所有符合条件的点P组成的图形.
24.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
参考答案
1.D
2.A
3.C
4.D
5.D
6.A
7.D
8.B
9.B
10.D
11.A
12.C
13.
14.(0,0)或(0,6)或(﹣4,0).
15.(10,0)
16.4个
17.4≤m≤8
18.(1,3)
19.(1)如图所示见解析;(2)21.
【详解】解:(1)如图所示:△A′B′C′即为平移后的三角形.
(2)△ABC在平移过程中扫过的面积=5×3+ ×4×3=15+6=21.
故答案为(1)如图所示见解析;(2)21.
20.(1),;(2);(3) 3
【详解】解:(1),;
(2)∵点到直线上一点的距离,垂线段最短
∴;
(3)如图所示:,就是所求的线段
三角形的面积:.
21.(1)见解析;(2)3;(3)平行;(4)点D到x轴的距离是5,点D到y轴的距离是3.
【详解】解:(1)如图:
;
(2)A点到原点的距离是3,
故答案为:3;
(3)∵CE的横坐标都是3,
∴直线CE与y轴平行;
(4)点D到x轴的距离是5,点D到y轴的距离是3.
22.(1)见解析
(2),
(3)
【详解】(1)解:根据题意补画得平面直角坐标系如图所示:
(2)根据图示坐标系各象限横纵坐标符号特点可得:A9(3,-2),A10(3,3);
(3)观察图形发现,下标为4n+2的点落在第一象限的对角线上,
∵A2(1,1), A6(2,2),
∴A4n+2(n+1,n+1),
∵2022=4×505+2,
∴A2022(506,506),
故答案为:(506,506).
23.(1)6
(2)
(3)1或-2,图见解析
【详解】(1)解:由题意可知:d(A,B)=|2-(-3)|+|1-0|=5+1=6;
(2)解:∵d(C,D)=2+|a|≤3,
∴|a|≤1,
∴-1≤a≤1;
(3)解:d(P,M)=|x|+|y-2|,d(P,N)=|x|+|y+3|,
由题意可知:||y-2|-|y+3||=3,
当y<-3时,
等式的左边=5,此时不满足题意;
当-3<y<2时,
等式的左边=|2y+1|,
即|2y+1|=3,
解得:y=1或y=-2,
当y>2时,
等式的左边=5,不符合题意,
综上所述,点P(x,1)或(x,-2),
如图所示.
.
24.见解析
试题解析:(1)三角形向下平移7个单位得到三角形
(2)三角形向右平移6个单位,再向下平移3个单位得三角形
