等腰三角形[上学期]
图片预览






文档简介
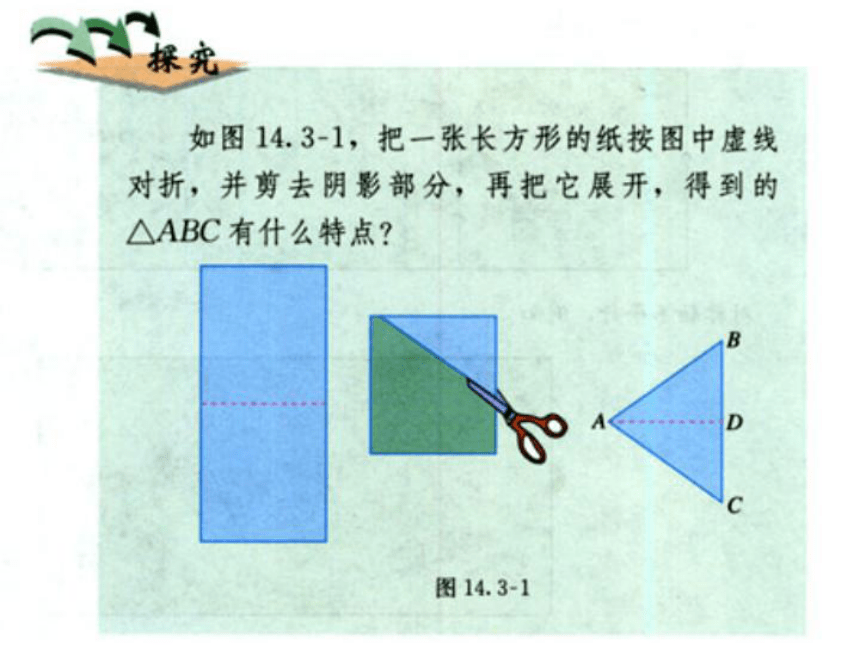
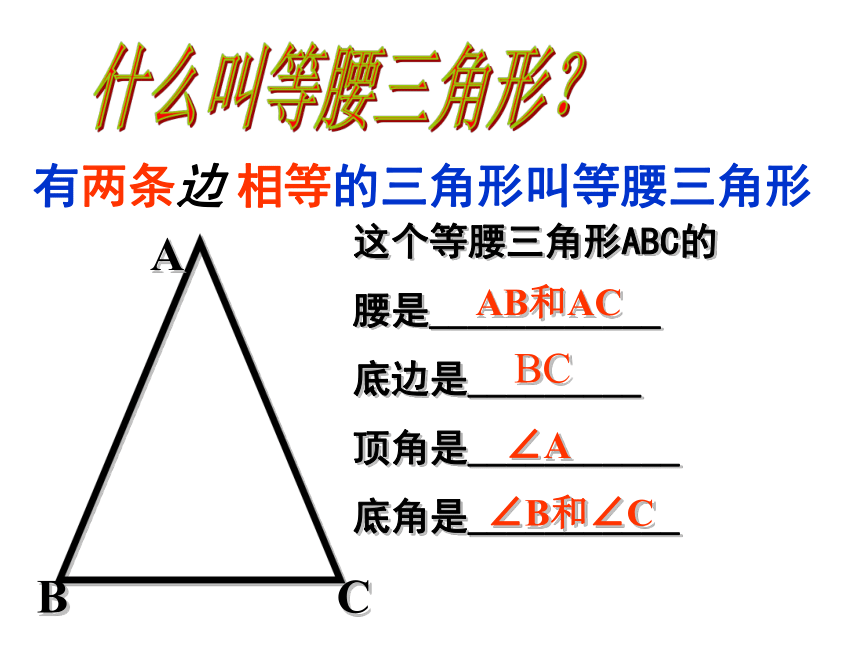
课件35张PPT。14.3.1等腰三角形(1)生活中的三角形等腰三角形你知道什么是等腰三角形吗?什么叫等腰三角形?有两条边 相等的三角形叫等腰三角形这个等腰三角形ABC的
腰是____________
底边是_________
顶角是___________
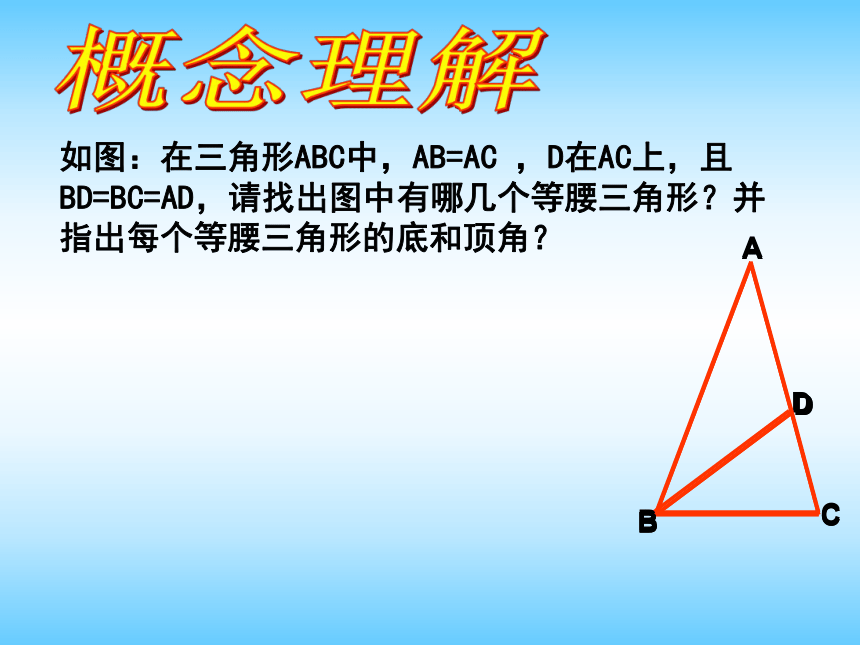
底角是___________AB和ACBC∠A∠B和∠C如图:在三角形ABC中,AB=AC ,D在AC上,且BD=BC=AD,请找出图中有哪几个等腰三角形?并指出每个等腰三角形的底和顶角?ACDB概念理解大胆猜测等腰三角形除了两腰相等以外,
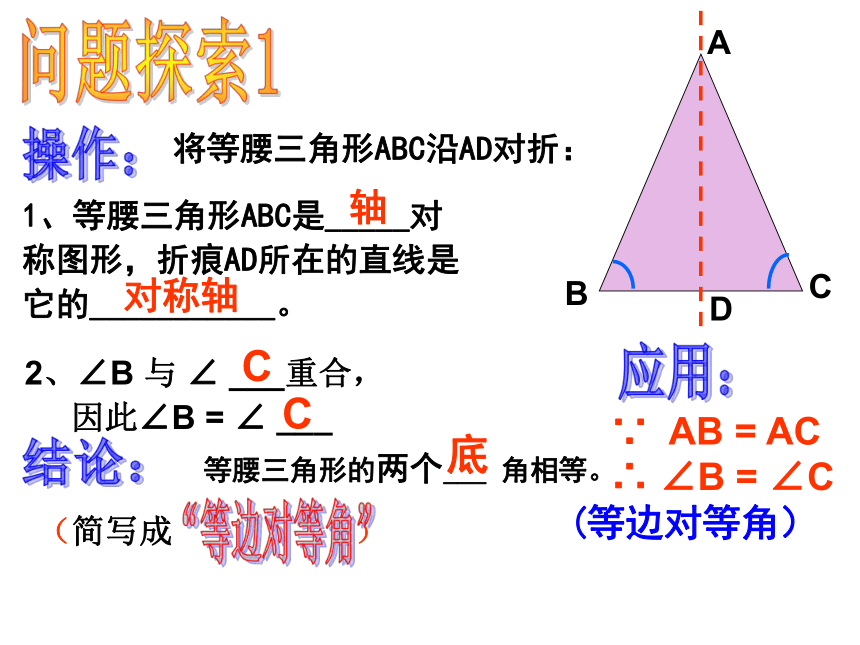
你还能发现什么?问题探索1
1、等腰三角形ABC是_____对
称图形,折痕AD所在的直线是它的___________。2、∠B 与 ∠ ___重合,
因此∠B = ∠ ___等腰三角形的两个___ 角相等。 ∵ AB = AC
∴ ∠B = ∠C
(等边对等角)操作:结论:应用:将等腰三角形ABC沿AD对折:轴对称轴CC底ABCD等腰三角形的性质:
性质1 等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。
已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD怎么证呢?证明: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.方法2:作底边中线等腰三角形的两个底角相等还有其它方法吗?证明: 作底边高线AD.
在Rt△BAD和△RtCAD中,AB=AC ( 已知 ),AD=AD (公共边) ,∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等方法3:作底边的高线还有其它方法吗?问题探索2操作: 画等腰△ABC顶角的平分线、底边上的高和底边上的中线。ACB结论: 等腰三角形顶角的平分线、底边的高和底边的中线互相_______。重合(简称“三线合一”)
1、∵ AB=AC, AD⊥BC,
∴ ∠ =∠ , = 。
2、∵ AB=AC, AD是中线
∴ ⊥ , ∠ = ∠ .
3、∵ AB=AC, AD是角平分线
∴ ⊥ , = 。BADCADBDCDBADADBCCADADBCBDCD应用:┓顶角的平分线底边的高底边的中线等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合。性质2: 怎么证呢?证明:∵AD是∠BAC角平分线,∴∠1=∠2
在△ABD和△ACD中
AB=AC (已知)
∠1=∠2 (已证)
AD=AD (公共边)
∴ △ABD ≌△ACD (SAS)∴BD=CD , ∠ADB= ∠ADC
∵ ∠ADB+ ∠ADC=180° ∴ ∠ADB= ∠ADC=90 °
∴AD 平分 BC,并且 AD ⊥ BC.
性质1:等腰三角形的两个底角相等 。
(简写成 “等边对等角”)等腰三角形的性质(三线合一)性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合。归纳:问:“三线合一”对于所有
的三角形都适用吗?等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?解:∵AB=AC,AD⊥BC
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm
∴CD=2cm,BC=4cm用一用2.在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠BAC=______度?解:∵AB=AC,AD ⊥BC
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20°
∴ ∠ 2=20°
∠BAC=40°等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用3.在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。解:∵AB=AC(已知)
∴△ABC是等腰三角形
∵BD=CD(已知)
∴BD⊥CD(等腰三角形三线合一)
∴线段AD的长度
就是点A到线段BC的
距离即为4 cm等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用4.已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用一休学数学
在三角形ABC中,已知AB=AC,且
要证∠1=∠2,如何去证?
这道题因被墨水遮去了
一个条件,一休无从下手,
现在请同学们帮一休补
上这个条件,使一休
能做出这道题。怎么办?等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用解:可补AD⊥BC于D或BD=CD等思考:等腰三角形的底角可以是直角或钝角吗?为什么?(不能,因为等腰三角形两底角相等,若底角是直角或钝角,三角形的内角和大于180°)例1、已知在△ABC中, AB=AC, [变式3] ∠A=200 且AC//BD,求∠CBD的度数[变式1] 有一个内角为800 ,求∠C和∠A的度数. [变式2] 有一个内角是1000 ,求∠C和∠A的度数. 典型例题∠B=800 ,求∠C和∠A的度数.等腰三角形的一个角可能指底角,也可能指顶角,须分情况讨论,但顶角可以是锐角、直角、钝角,而底角只能是锐角
解: ∵AB=AC∴∠B=∠C①若∠B=∠C=800
在△ABC 中∠A+ ∠B+∠C=1800
即 ∠A= 1800-∠B-∠C=200例题讲解例1:已知:在等腰△ABC中, ,∠B=800,
求∠ C 和 ∠A的度数?
1、 AB=AC表示AB和AC是三角形的___,
底角是∠___和∠___。
2、先应根据__________, 求出∠___。
3、再根据 _____________, 求出∠___。腰等边对等角C三角形的内角和ABC 画图、讨论:解:∵AB=AC
∴ ∠C= ∠B=800 (等边对等角)
∵ ∠A+ ∠B+ ∠C=1800 ( ? )
∴ ∠A=1800- 800- 800=200AB=AC例2:已知:在等腰△ABC中,∠B=800,
求:∠ C 和 ∠A的度数?例题变式(图一)讨论:∠B的位置有几种可能?
(可能是底角或顶角)分析:当∠B为底角时, ∠C为800,
∠A为200;当∠B为顶角时, ∠C为500,
∠A为500。题组训练题组1: ①如果等腰三角形的一个底角为500,
则其余两个角为____和___。②如果等腰三角形的顶角为800,
则它的一个底角为___。500800500题组训练题组2:1、等腰三角形的一个内角为1200,则另两角为_________。2、等腰三角形的一个外角为1300,则三个内角分别为:_______________________________。3、等腰三角形的一个内角是另一个内角的2倍,则三
个内角分别为:_______________________________。
分析:设小角为α,则大角为2α.当α为底角时, α +α+ 2α=1800
解得 α=450,则2α=900当2α为底角时, α +2α+ 2α=1800
解得α =360,则2α=720∴其内角的度数为450,450,900,或360,720,720.300和300650、650、500或500、500、800450、450、900或360、720、720如图:在三角形ABC中,AB=AC , D在AC上,且BD=BC=AD,求△ABC各内角的度数?请你解决问题123解:设∠A=x, ∵BD=AD, ∴ ∠1= ∠A=x∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A=2x∵ BD=BC, ∴ ∠3= ∠C = 2 ∠A=2x∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A=2x∵ ∠A+ ∠ABC+ ∠C=1800,
∴ x +2x+2x=1800,
∴x=360
即 ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。趣味数学分析:应该利用什么思想呢?转化思想2、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;1、熟练求解等腰三角形的顶
角、底角的度数;
3、掌握等腰三角形三线合一的应用。再见
腰是____________
底边是_________
顶角是___________
底角是___________AB和ACBC∠A∠B和∠C如图:在三角形ABC中,AB=AC ,D在AC上,且BD=BC=AD,请找出图中有哪几个等腰三角形?并指出每个等腰三角形的底和顶角?ACDB概念理解大胆猜测等腰三角形除了两腰相等以外,
你还能发现什么?问题探索1
1、等腰三角形ABC是_____对
称图形,折痕AD所在的直线是它的___________。2、∠B 与 ∠ ___重合,
因此∠B = ∠ ___等腰三角形的两个___ 角相等。 ∵ AB = AC
∴ ∠B = ∠C
(等边对等角)操作:结论:应用:将等腰三角形ABC沿AD对折:轴对称轴CC底ABCD等腰三角形的性质:
性质1 等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。
已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD怎么证呢?证明: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.方法2:作底边中线等腰三角形的两个底角相等还有其它方法吗?证明: 作底边高线AD.
在Rt△BAD和△RtCAD中,AB=AC ( 已知 ),AD=AD (公共边) ,∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等方法3:作底边的高线还有其它方法吗?问题探索2操作: 画等腰△ABC顶角的平分线、底边上的高和底边上的中线。ACB结论: 等腰三角形顶角的平分线、底边的高和底边的中线互相_______。重合(简称“三线合一”)
1、∵ AB=AC, AD⊥BC,
∴ ∠ =∠ , = 。
2、∵ AB=AC, AD是中线
∴ ⊥ , ∠ = ∠ .
3、∵ AB=AC, AD是角平分线
∴ ⊥ , = 。BADCADBDCDBADADBCCADADBCBDCD应用:┓顶角的平分线底边的高底边的中线等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合。性质2: 怎么证呢?证明:∵AD是∠BAC角平分线,∴∠1=∠2
在△ABD和△ACD中
AB=AC (已知)
∠1=∠2 (已证)
AD=AD (公共边)
∴ △ABD ≌△ACD (SAS)∴BD=CD , ∠ADB= ∠ADC
∵ ∠ADB+ ∠ADC=180° ∴ ∠ADB= ∠ADC=90 °
∴AD 平分 BC,并且 AD ⊥ BC.
性质1:等腰三角形的两个底角相等 。
(简写成 “等边对等角”)等腰三角形的性质(三线合一)性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合。归纳:问:“三线合一”对于所有
的三角形都适用吗?等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?解:∵AB=AC,AD⊥BC
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm
∴CD=2cm,BC=4cm用一用2.在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠BAC=______度?解:∵AB=AC,AD ⊥BC
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20°
∴ ∠ 2=20°
∠BAC=40°等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用3.在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。解:∵AB=AC(已知)
∴△ABC是等腰三角形
∵BD=CD(已知)
∴BD⊥CD(等腰三角形三线合一)
∴线段AD的长度
就是点A到线段BC的
距离即为4 cm等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用4.已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用一休学数学
在三角形ABC中,已知AB=AC,且
要证∠1=∠2,如何去证?
这道题因被墨水遮去了
一个条件,一休无从下手,
现在请同学们帮一休补
上这个条件,使一休
能做出这道题。怎么办?等腰三角形的性质
1.等腰三角形的两个底角相等(等边对等角)
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
用一用解:可补AD⊥BC于D或BD=CD等思考:等腰三角形的底角可以是直角或钝角吗?为什么?(不能,因为等腰三角形两底角相等,若底角是直角或钝角,三角形的内角和大于180°)例1、已知在△ABC中, AB=AC, [变式3] ∠A=200 且AC//BD,求∠CBD的度数[变式1] 有一个内角为800 ,求∠C和∠A的度数. [变式2] 有一个内角是1000 ,求∠C和∠A的度数. 典型例题∠B=800 ,求∠C和∠A的度数.等腰三角形的一个角可能指底角,也可能指顶角,须分情况讨论,但顶角可以是锐角、直角、钝角,而底角只能是锐角
解: ∵AB=AC∴∠B=∠C①若∠B=∠C=800
在△ABC 中∠A+ ∠B+∠C=1800
即 ∠A= 1800-∠B-∠C=200例题讲解例1:已知:在等腰△ABC中, ,∠B=800,
求∠ C 和 ∠A的度数?
1、 AB=AC表示AB和AC是三角形的___,
底角是∠___和∠___。
2、先应根据__________, 求出∠___。
3、再根据 _____________, 求出∠___。腰等边对等角C三角形的内角和ABC 画图、讨论:解:∵AB=AC
∴ ∠C= ∠B=800 (等边对等角)
∵ ∠A+ ∠B+ ∠C=1800 ( ? )
∴ ∠A=1800- 800- 800=200AB=AC例2:已知:在等腰△ABC中,∠B=800,
求:∠ C 和 ∠A的度数?例题变式(图一)讨论:∠B的位置有几种可能?
(可能是底角或顶角)分析:当∠B为底角时, ∠C为800,
∠A为200;当∠B为顶角时, ∠C为500,
∠A为500。题组训练题组1: ①如果等腰三角形的一个底角为500,
则其余两个角为____和___。②如果等腰三角形的顶角为800,
则它的一个底角为___。500800500题组训练题组2:1、等腰三角形的一个内角为1200,则另两角为_________。2、等腰三角形的一个外角为1300,则三个内角分别为:_______________________________。3、等腰三角形的一个内角是另一个内角的2倍,则三
个内角分别为:_______________________________。
分析:设小角为α,则大角为2α.当α为底角时, α +α+ 2α=1800
解得 α=450,则2α=900当2α为底角时, α +2α+ 2α=1800
解得α =360,则2α=720∴其内角的度数为450,450,900,或360,720,720.300和300650、650、500或500、500、800450、450、900或360、720、720如图:在三角形ABC中,AB=AC , D在AC上,且BD=BC=AD,求△ABC各内角的度数?请你解决问题123解:设∠A=x, ∵BD=AD, ∴ ∠1= ∠A=x∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A=2x∵ BD=BC, ∴ ∠3= ∠C = 2 ∠A=2x∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A=2x∵ ∠A+ ∠ABC+ ∠C=1800,
∴ x +2x+2x=1800,
∴x=360
即 ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。趣味数学分析:应该利用什么思想呢?转化思想2、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;1、熟练求解等腰三角形的顶
角、底角的度数;
3、掌握等腰三角形三线合一的应用。再见
