广西南宁市名校2022-2023学年高二下学期期中考试数学试题(PDF版含解析)
文档属性
| 名称 | 广西南宁市名校2022-2023学年高二下学期期中考试数学试题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 633.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 09:44:35 | ||
图片预览




文档简介
南宁名校 2022~2023学年度下学期高二期中考试
数学试题
考试时间:120 分钟 满分:150 分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上写在本试卷上无效.
一、单选题:本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有一项
符合题目要求.
1 2.已知集合 A x x 9 , B x | 1 x 5, x N ,则 A B ( )
A. 1,3 B. 0,5 C. 1,2 D. 0,1,2
2.若复数 z满足 i z 3 4i,则 z ( )
A.1 B.5 C.7 D.25
3.设 a R,则“ a 1”是“直线 l1: ax 2y 4 0与直线 l2: x a 1 y 2 0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.记等差数列 an 的前 n项和为 Sn,若 S11 44,则 a4 a6 a8 ( )
A.12 B.13 C.14 D.15
1
5. 函数 f (x) x3 4x2 9x 6在区间[-1,2]上的最小值为( )
3
56 20 4
A. B. C. D. 3
3 3 3
6. 已知圆的方程为 x2 y2 6x 8y 0,设该圆过点 3,5 的最长弦和最短弦分别为 AC和 BD,
则四边形 ABCD的面积为( )
A.10 6 B. 20 6 C.30 6 D. 40 6
x27 y
2
.已知 F为双曲线C : 2 2 1(a 0,b 0)的左焦点,直线 l经过点 F,若点 A(a,0),B(0,b)a b
关于直线 l对称,则双曲线 C的离心率为( )
A 3 1 B 2 1. . C. 3+1 D. 2+1
2 2
ln3
8 a 10.已知 ln10,b 2 2 , c ,则( )
20 e3 3
A. a c b B. c b a C.b a c D.b高二期中考试 数学试卷 第 1页 共 4页
二、多选题:本题共 4 小题,每小题 5 分,共 20 分在每小题给出的选项中,有多项符合题目要
求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 2 分.
9.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”、“乐”、“射”、“御”、
“书”、“数”六门体验课程,每周一门,连续开设六周,则下列说法正确的是( )
A.某学生从中选 2门课程学习,共有 15种选法
B.课程“乐”“射”排在不相邻的两周,共有 240种排法
C.课程“御”“书”“数”排在相邻的三周,共有 144种排法
D.课程“礼”不排在第一周,也不排在最后一周,共有 480种排法
10.已知等比数列{an}的公比为q,前n项积为Tn,若a1 128,且T7 T8 ,则下列命题正确的是( )
A. a8 1 B.当且仅当 n 8时,Tn 取得最大值
1
C q D. a a a *.
2 1 2 n
a1 a2 a15 n n N ,n 15
11 2.已知抛物线C : x 2py p 0 的焦点为 F,点 A 2,1 在 C上,P为 C上的一个动点,则( )
A.C的准线方程为 x= 1
B.若M 0,3 ,则 PM 的最小值为2 2
C.若M 3,5 ,则△PMF的周长的最小值为 11
D.在 x轴上存在点 E,使得 PEF为钝角
1
12. 已知函数 f x e2x , g x lnx 分别与直线 y a交于点 A,B,则下列说法正确的( )
2
A. AB
1
的最小值为 ln2 1
2
B. a R,使得曲线 y f x 在点 A处的切线与曲线 y g x 在点 B处的切线平行
C.函数 y f x g x 的最小值小于 2
D.若 2 x e f x 3 2g x ,则 x e
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
( x 113 5.在代数式 2 ) 的展开式中,常数项为_____________.x
2x 1
14.曲线 y 在点 ( 1, 3)处的切线方程为__________.
x 2
15.某班宣传小组有 3名男生和 2名女生.现从这 5名同学中挑选 2人参加小剧场演出,在已知
抽取到有男生的条件下,2名都是男生的概率为___________.
16.已知函数 f x x ln x ae x( e为自然对数的底数)有两个极值点,则实数 a的取值范围是
___________.
高二期中考试 数学试卷 第 2页 共 4页
四、解答题:本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
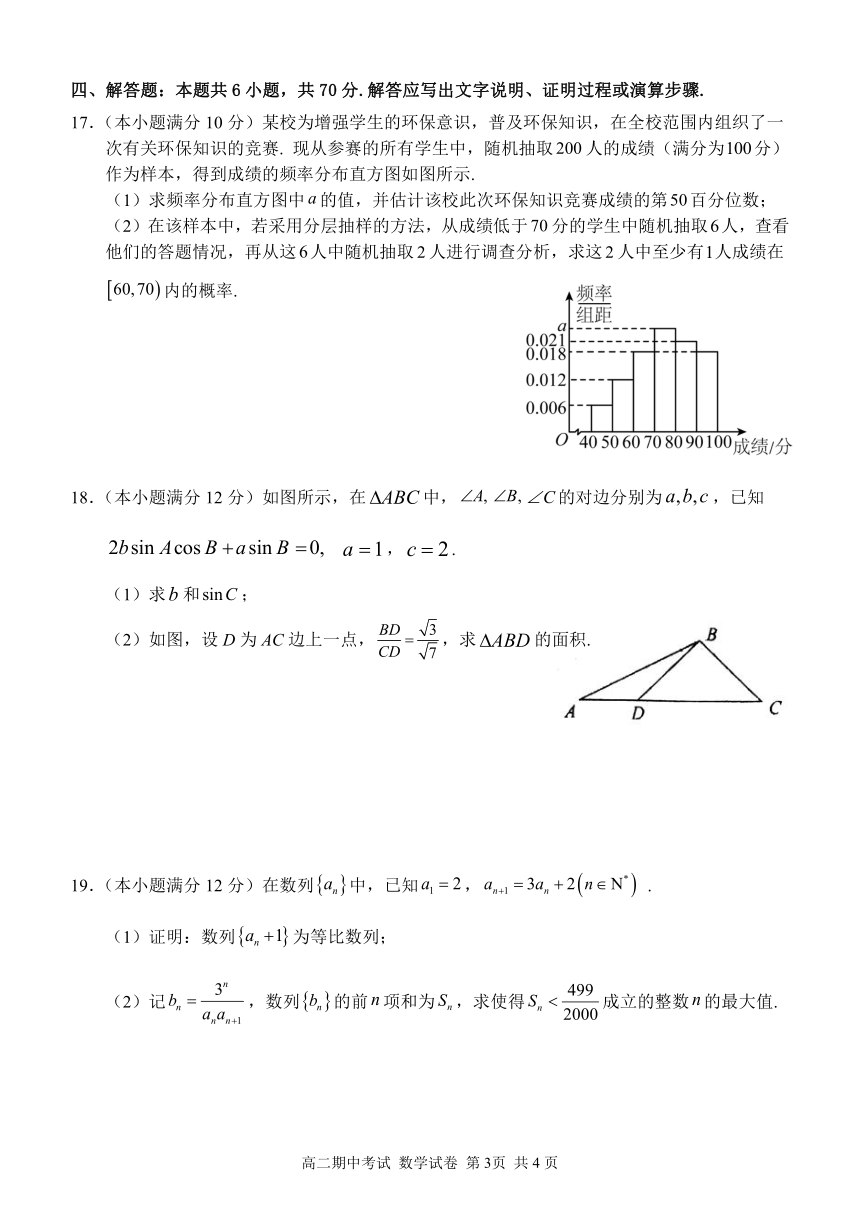
17.(本小题满分 10分)某校为增强学生的环保意识,普及环保知识,在全校范围内组织了一
次有关环保知识的竞赛. 现从参赛的所有学生中,随机抽取 200人的成绩(满分为100分)
作为样本,得到成绩的频率分布直方图如图所示.
(1)求频率分布直方图中 a的值,并估计该校此次环保知识竞赛成绩的第50百分位数;
(2)在该样本中,若采用分层抽样的方法,从成绩低于70分的学生中随机抽取6人,查看
他们的答题情况,再从这6人中随机抽取 2人进行调查分析,求这 2人中至少有1人成绩在
60,70 内的概率.
18.(本小题满分 12分)如图所示,在 ABC中, A, B, C的对边分别为 a,b,c,已知
2bsin AcosB a sin B 0, a 1, c 2 .
(1)求b和sinC;
(2 BD 3)如图,设 D为 AC边上一点, ,求 ABD的面积.CD 7
19.(本小题满分 12分)在数列 an 中,已知 a1 2, an 1 3an 2 n N* .
(1)证明:数列 an 1 为等比数列;
b 3
n 499
(2)记 n ,数列 bn 的前 n项和为 Sn,求使得 S 成立的整数n的最大值.ana nn 1 2000
高二期中考试 数学试卷 第 3页 共 4页
20.(本小题满分 12分)如图,在多面体 ABCDEF 中,四边形 ABCD是边长为 4的菱形,
BCD 60 , AC与 BD交于点O,平面FBC 平面 ABCD, EF // AB, FB FC,且
EF 2 .
(1)求证:OE 平面 ABCD;
(2)若 AE FC,点Q为 AE的中点,求二面角Q BC A的余弦值.
2 2
21.(本小题满分 12分)已知椭圆C : x y2 2 1(a b 0),四点 P1(0,2),P2 (1,1),P3( 2,1),a b
P4 ( 2,1)恰有三点在C上.
(1)求C的方程;
2 x2 y2
4
( )若圆 的切线 l与C交于点 A,B,证明:OA OB .
3
2ae2x22.(本小题满分 12分)已知函数 f x ,a 0 .
x
(1)讨论函数 f x 的单调性;
(2)若 ln x xf x lna恒成立,求实数 a的取值范围.
高二期中考试 数学试卷 第 4页 共 4页
南宁名校 2022~2023学年度下学期高二期中考试
数学试题参考答案
1.D【详解】集合 A x | x2 9 x | 3 x 3 ,集合 B x | 1 x 5, x N 0,1,2,3,4 ,
则 A B 0,1, 2 ,故选:D.
z 3 4i 3 4i i 2.B【详解】由题意有 4 3ii i i ,故 | z | 4
2 3 2 5.故选:B.
3.C【详解】解:当 a 1时, l1: x 2y 4 0 l x 2y 2 0
1 2 4
, 2: , ,可得两直线1 2 2
平行;若l1与l
a 2 4
2平行,则 ,解得a 1或a 2(舍 ),故为充要条件,故选:C.1 a 1 2
4.A【详解】根据数列 a 11 a a n 为等差数列,则 S 1 1111 11a6 44,所以 a6 4,所以2
a4 a6 a8 3a6 12,故选:A.
1
5.C【详解】由 f (x) x3 4x2 9x 6, x [ 1,2]可得 f (x) x 2 8x 9,令 f (x) 0,解得
3
x 1,当 1 x 1, f (x) 0, f (x)单调递减;当1 x 2, f (x) 0, f (x)单调递增,所以 f (x)
1 4
的极小值,也为最小值为 f (1) 4 9 6 ,故选:C
3 3
6.B【详解】解:圆心坐标是 3, 4 ,半径是 5,圆心到点 3,5 的距离为 1.
所以点 3,5 在圆内,最长弦为圆的直径。由垂径定理得:最短弦 BD和最长弦(即圆的直径)
AC垂直,故最短弦的长为2 52 12 4 6 ,最长弦即直径,即 AC 10,
1
所以四边形 ABCD的面积为 AC BD
1
10 4 6 20 6.故选:B.
2 2
7.C【详解】解法一:由点 A(a,0),B(0,b)关于直线 l对称,
a bl
b
可得直线 为线段 AB的垂直平分线,线段 AB的中点的坐标为 , ,直线 AB的斜率为 ,
2 2 a
b a a 2 2
可得直线 l的方程为 y- x
1 b 1 b
2 b 2
,令 y=0,可得 x= a ,由题意可得-c a ,
2 2a 2 2a
c
即有 a(a+2c)=b2=c2-a2,即 c2-2ac-2a2=0,由 e= ,可得 e2-2e-2=0,
a
解得 e=1 3 ( e=1 3舍去),故选:C.
高二期中考试 数学答案 第 1页 共 10页
解法二:由点 A(a,0),B(0,b)关于直线 l对称,可知 AF BF ,即 a c b2 c2 ,
两边平方,并结合b2 c2 a2,整理可得 c2-2ac-2a2=0,下同解法一.
f x ln x 1 ln x8.C【详解】设函数 x e ,则 f x 2 0,则 f x 在 e, 上是减函数,x x
又 e 3 10 e3,则 f 3 f 10 f e3 ,
f 10 ln 10 10
3 ln 3
又因为 ln10 a f e3 ln e 3 2 2, , f 3 c ,10 20 e3 e3 e3 3
所以 f 3 f 10 f e3 b,即b a c.故选:C.
9.ACD 2【详解】对于 A,从六门课程中选两门的不同选法有C6 15种,A正确;
对于 B 4 2,先排“礼”、“御”、“书”、“数”,再用插空法排“乐”“射”,不同排法共有 A4 A5 480种,
B错误;对于 C,“御”“书”“数”排在相邻的三周,可将“御”“书”“数”视为一个元素,不同排法
A3A4共有 3 4 144种,C正确;对于 D,从中间四周中任取一周排“礼”,再排其它五门体验课程
共有 4A55 480种,D正确.故选:ACD.
10.ACD【详解】因为T7 T8 ,所以a8 1,故 A正确;
n 1 7 1 1
又 a8 a1q ,即 q ,解得 q ,故 C正确;128 2
由 q
1
知等比数列{an}为递减数列,且a8 1,故Tn取得最大值为T7 T8,故 B错误;2
n (n 1) n(n 15)
因为 a a a a nq1 2 n 11 2 n 1 (q
7 )nq 2 q 2 ,
(14 n)(15 n) n2 15n n(n 15)
a a a a 15 nq1 2 14 n (q 7 )15 n 2 2 21 2 15 n 1 q q q
*
所以 a1 a2 an a1 a2 a15 n n N ,n 15 成立,故 D正确. 故选:ACD
11.BC【详解】A选项:因为点 A 2,1 在抛物线C : x2 2 py上,所以 22 2 p,解得 p 2,
所以抛物线 C的方程为 x2 4y,所以 C的准线方程为 y 1,故 A错误;
B 2选项:设点 P(x0,y0 ), y0 0,则 x0 4y0 ),
因为M 0,3 2,所以 PM x20 y0 3
2 y20 2y0 9 y
2
0 1 8 8,
高二期中考试 数学答案 第 2页 共 10页
当且仅当 y0 1时等号成立,所以 PM 2 2min ,故 B正确;
C选项:过点 P作PN垂直于 C的准线,垂足为 N,连接 MN,则 PN PF ,
易知 F 0,1 ,M 3,5 2,所以 MF 32 5 1 5,
所以△PMF 的周长为 MF MP PF MF MP PN MF MN 5 6 11,
当且仅当 M,P,N三点共线时等号成立,
所以△PMF 的周长的最小值为 11,故 C正确;
D选项:设 E t, 0 ,则 EF t,1 , EP x0 t, y0 ,
所以 EF EP t x0 t y 20 t x0t y0,
2
因为点 P(x0,y0 )在 C上,所以 x
2
0 4y
x
0 ),即 y 00 ,4
2 2
所以 EF EP t 2 x 0t
x
0 t
x
0 0,4 2
EF EP
所以 cos PEF 0 ,故 PEF不可能为钝角,故 D错误.EF EP
故选:BC.
1
12 AB 2x. 【详解】对于 A项,设 A x1,a , B x2 ,a ,则 f x1 e 1 a, x1 lna,2
1 a 1 a
1
1
又因为 g x2 lnx2 a, x 2 ,所以 AB x2 x1 e 2 lna a 0 ,2 2 e 2
a 1 a 1
设 a =e 2 1 ln a a 0 ,所以 a =e 2 1 a 0 ,
2 2a
a 1 1 1
又因为 a =e 2 1 在 0, 0单调递增,且 =e 1 0 ,当 a 0, , a 0;,2a 2 2
a 1当 , , a
1 1
0 a 0, 所以 在 上单调递减,在 , 单调递增,
2 2 2
a 1 1 1 1所以 e0 ln 1 ln 2
1
,所以 AB 的最小值为 ln2 1,故 A正确.
2 2 2 2 2
对于 B项,函数 f x e2x A x ,a f x 2e2x在点 1 处切线的斜率为 11 ,
又因为 x
1
1 lna
2x
,所以函数 f x e 在点 A x1,a 处切线的斜率为2
高二期中考试 数学答案 第 3页 共 10页
2 1 ln a
f x 2e2x11 2e 2 2a,
1
函数 g x lnx 1 在点 B x ,a 处切线的斜率为 g x ,
2 2 2 x2
a 1 1 1 1又因为 x e 2 ,所以函数 g x lnx 在点 B x2 ,a 处切线的斜率为 g x2 2 2 x2 a 1 ,e 2
要使曲线 y f x 在点A处的切线与曲线 y g x 在点 B处的切线平行,即
1 1
f x1 g x2 2a
1 a
,所以 a 1 有解,即方程
a
2a e 2 1 0 有根.即函数 h a 2a e 2 1有e 2
零点,
a 1 h 1 1
1 1
又因为当 , 2 e 2 2 1 0 ,故 B正确.2 2 2
C y f x g x e2x对于 项, ln x 1 1 2x,因为 y 2e 在 0, 上单调递增,
2 x
2 1
2 1
x 1 y 2e 1 2e 2 2 e 1 0当 时, ,
2
2
2 1 1
x 1 y 2e
4 1 2
当 时, 1 2e 4 2 e 2 0,
4
4
x 1 , 1 2x
1 1
则存在 0
2x0
0 ,使得 2e 0,即 e , ln 2 2x0 ln x0 ,
4 2 x0 2x0
当 x 0, x0 时, y 0; x x0 , 时, y 0,
y y e2x ln x 1 1 2x ln 2 1所以 min x x 0 0 0 2
1 2x ln 2 1 2 ln 2 1 0 0 2 2x ,0 2 2x0 2 2
1
(由于 x ,故等号取不到),
2
又因为 2
1
ln 2 2,函数 y f x g x 的最小值大于 2,故 C错误;
2
对于 D项,不等式2 x e f x 3 2g x 2x化简后变为: x e e ln x 1 0,
当 x 0,e 时, x e 0, ln x 1 0,e 2x 0 , x e e2x ln x 1 0,
当 x e, 时, x e>0, ln x 1 0,e 2x 0 , x e e2x ln x 1 0,
所以 2 x e f x 3 2g x ,则 x e,故 D错误.
高二期中考试 数学答案 第 4页 共 10页
5 1 5 r r 5 5r
13.-5 x 1 1 r【详解】 2 的展开式的通项为:T C
r 2
r 1 5 x 2 C
r 2
5x 1
x x
5 5r 5
令 0 1 1 ,解得 r 1,所以T 12 1 C5 1 5, x 2 的展开式中的常数项为 5 .2 x
14.5x y 2 0【详解】由题,当 x= 1时, y= 3,故点在曲线上.
2 x 2 2x 1 5
求导得: y ,所以 y | 5 .x 2 2 x 2 2 x 1
故切线方程为5x y 2 0.故答案为:5x y 2 0.
1
15. 【详解】设事件 A表示“有男生”,事件 B表示“两名都是男生”,
3
3
2 2 P AB
则 P(A) 1
C
2
9 C 3 1
3 12 , P(AB) ,故 P B A 10 .故答案为: .C5 10 C25 10 P A 9 3 3
10
16.0
1
a 【详解】 f x 1 ln x aex,因为函数 f x x ln x ae x( e为自然对数的底数)
e
有两个极值点,所以1 ln x aex 0在 0, 上有两个不等实根,
a 1 ln x 1 ln x x 在 0, 上有两个不等实根,令 g x ,e ex
1
1 ln x
g x x ,当 0 x 1时, g (x) 0,当 x 1时, g (x) 0,
ex
1
所以当 x 1时, f x 的最大值为 ;
e
当 x 0时, g x ,当 x 时, f x 0,
1
如图所示:所以实数 a的取值范围是0 a .
e
0 a 1故答案为:
e
4
17.(1)a 0.025,第50百分位数为75.6 (2)
5
解:(1)由频率分布直方图可得, 0.006 0.012 0.018 2 0.021 a 10 1,..............1分
则 a 0.025, ........................................................................2分
前 3组的频率和为 0.006 0.012 0.018 10 0.36,第 4组频率为0.25,所以第50百分位数
高二期中考试 数学答案 第 5页 共 10页
位于第 4组 70,80 内,记第 50百分位数为 x,.......................................................................3分
x 70 0.5 0.36
则 ,解得 x 75.6,即第 50百分位数为75.6;....................................5分
10 0.25
(2)由频率分布直方图可知,成绩在 40,50 , 50,60 , 60,70 内的频率分别为0.06,0.12,0.18,
采用分层抽样的方法从样本中抽取的 6人,成绩在 40,50 内的有 1人,记为A,成绩在 50,60
内的有 2人,记为 B1 B2,成绩在 60,70 内的有 3人,记为C1 C2 C3,.................................6分
则从成绩在 40,70 内的 6人随机抽取 2人,共有:
AB1 AB2 AC1 AC2 AC3 B1C1 B1C2 B1C3 B2C1 B2C2 B2C3 C1C2 C1C3 C2C3 B1B2,共有 15种,
2人中至少有 1人成绩在 60,70 内,共有:
AC1 AC2 AC3 B1C1 B1C2 B1C3 B2C1 B2C2 B2C3 C1C2 C1C3 C2C3,有 12种,............................8分
12 4
记事件 A “ 2人中至少有 1人成绩在 60,70 内”,则 P A .....................................10分
15 5
18. 1 a b c解( )因为 2bsin AcosB asin B 0 ,所以在 ABC中,由正弦定理 ,
sin A sin B sinC
得 2sin B sin Acos B sin Asin B 0,因为 sin Asin B 0 ,所以 2cosB 1 0,
cos B 1 2 所以 ,又0 B ,所以 B ,....................................3分
2 3
1
由余弦定理得,b2 a2 c2 2ac cosB 1 4 2 1 2
7,所以 ,
2
b 7
c b
在 ABC中,由正弦定理 ,
sinC sin B
2sin 2
所以 sinC
c sin B
3 21 ;....................................6分b
7 7
BD sinC
(2)在△ABD中,由正弦定理得, ,
CD sin CBD
BD 3 sinC 3 21
因为 ,所以 ,因为 sinC ,所以 sin CBD 1,
CD 7 sin CBD 7 7
而 CBD 0, ,所以 CBD ,....................................8分
2
BD 3 1
由 ,设 BD 3t , CD 7t,所以 ( 3t)2 12 ( 7t)2,所以 t 3,所以 BD ,
CD 7 2 2
高二期中考试 数学答案 第 6页 共 10页
2
因为 ABD ABC DBC ,....................................10分
3 2 6
所以 S
1
ABD AB BD sin ABD
1 3 1 3
2 2
.....................................12分
2 2 2 4
a 1 3 a 1
19.解(1)由 an 1 3an 2,得 an 1 1 3 a 1 n 1 nn , 3,又a 1 3,an 1 an 1 1
故数列 an 1 是以3为首项,3为公比的等比数列;....................................5分
n
2 a 1 3n a 3n b
3 1 1 1
( ) n ,故 n 1,故 n 3n 1 3n 1 1 2 3n 1 3n 1 1 ,......................8分
S 1 1 1 1 1 1 1 1 1 1 1 1n 1 2 2 3
2 3 1 3 1 2 3 1 3 1 2 3n 1 3n 1
n 1 ,...........10分 1 4 2 3 1
S 499 1 1 1 499n ,即 n 1 ,即3n 1 1001,36 1001 37 ,故 n 5,2000 4 2 3 1 2000
故使得 S
499
n 成立的最大整数为5 .....................................12分2000
20.(1)证明:如图,取 BC中点G,连接 FG,OG,
因为 FB FC,所以 FG BC,
又因为平面FBC 平面 ABCD,平面 FBC 平面 ABCD BC, FG 平面FBC,
所以 FG 平面 ABCD, O,G分别为 AC,BC
1
中点,所以OG∥ AB,OG AB .
2
1
因为EF AB,EF / /AB, EF / /OG,EF OG
2
所以四边形EFGO为平行四边形,所以OE∥FG,所以OE 平面 ABCD ..........................6分
(2)如图,以 AC所在直线为 x轴, BD所在直线为 y轴,OE所在直线为 z轴建立空间坐标
系,设OE 0,0,c , (c 0)
A 2 3,0,0 ,B 0, 2,0 ,C 2 3,0,0 ,Q c 3,0,
2
F 3,1,c ,CF 3,1,c ,CF AE 0, c 6 6,Q 3,0,
2
设平面QBC的法向量 v x, y, z ,BC 2 3, 2,0 ,BQ 3, 2,
6
2
高二期中考试 数学答案 第 7页 共 10页
v
BQ 0
2 3x 2y 0
则
即 6 ,则 v 1, 3, 3 2 .
v BC 0 3x 2y z 0 2
设平面 ABC的法向量 n 0,0,1 ,设二面角Q BC A的平面角为 , 为锐
角,....................................10分
n v 3 11 3 11
所以 cos .二面角Q BC A的余弦值 .....................................12分n v 11 11
2 2
21.(1) x y 1; (2)证明见解析
4 2
【详解】(1)由 P y3 ,P4 两点关于 轴对称,可得C经过 P3 ,P4 两点.
P2与P3的纵坐标相同,且都位于第一象限,不可能都在C上,所以 P2不在C上,
b 2,
a 2, C x
2 y2
则 2 1 解得 故 的方程为 1.....................................4分
2 2 1, b 2. 4 2 a b
2 2 3( )证明:当切线 l的斜率不存在时,得 l : x .
3
2 3 2 3 2 3 2 3
当 l : x 2 3 时,可得 A
3
,
3 3
,B , .
3 3
OA OB 2 3 2 3 2 3 2 3 0,则OA OB .....................................6分
3 3 3 3
当 l : x 2 3 时,同理可证.
3
当切线 l的斜率存在时,设 l : y kx m .
l x2 y2 4
m 2 3 2 2
因为 与圆 相切,所以圆心 0,0 到 l的距离为 ,即3m 4 k 1 .
3 k 2 1 3
y kx m,
联立 x2 y2 得 2k 2 1 x2 4kmx 2m2 4 0 .
1, 4 2
A x , y ,B x , y x x 4km
2
设 1 1 2 2 ,则 1 2 2 , x x
2m 4
1 2 2 .....................................8分1 2k 1 2k
OA OB x 2 21x2 y1y2 x1x2 (kx1 m)(kx2 m) (k 1)x1x2 km(x1 x2 ) m
高二期中考试 数学答案 第 8页 共 10页
k 2 1 2m2 4 4k 2m2 4k 2 3m2 4
m2
1 2k 2 1 2k 2 1 2k 2
2 2 由3m 4 k 1 ,得OA OB 0,则OA OB .
x2 y2 4综上,若圆 的切线 l与C交于点 A,B,则OA OB .....................................12分
3
1
22. (1)见解析; (2) ,
2e
2ae2 x 4ae2 x 2 x 2 x1 f x x 2ae 2ae 2x 1解:( )因为 ,所以 f x .
x x2 x2
1 1
当a 0时,由 f (x) 0,得 x ,由 f x 0,得 x ,且 x 0,
2 2
故 f x 1 1 的单调递增区间为 , ,单调递减区间为 ,0 , 0, ;
2 2
当 a<0时,由 f (x) 0 x 1,得 ,且 x 0,由 f x 0 x 1,得 ,
2 2
故 f x 1 1 的单调递增区间为 ,0 , 0, ,单调递减区间为2 , . 2
a 0 f x 1 1 综上,当 时, 的单调递增区间为 , 2 ,单调递减区间为 ,0 , 0, ; 2
当 a<0时, f x 的单调递增区间为 ,0 , 0,
1
2
,
1 , 单调递减区间为 .....................................5分
2
(2)易知 x 0, a 0 .
2x x
由 ln x xf x lna,可得 2ae ln x ln a ln ,
a
x
2xe2x x
ln
所以 ln
x
恒成立,即 2xe2x e a ln x恒成立.
a a a
设u x xex x 0 u x x 1 ex, ,则 0,所以 u x 在 0, 上单调递增.
x
当 x 0时,u x 0 ln,所以2xe2x e a ln x x恒成立等价于2x ≥ ln 恒成立,
a a
x
即a ≥ 对 x 0, 恒成立.
e2x
v x x 1 2x设 , x 0, v x .
e2x e2x
x 0, 1 当 时, v x 0
1
;当 x , 时, v x 0 .
2 2
高二期中考试 数学答案 第 9页 共 10页
所以 v x 在 0,
1 1
上单调递增,在 , 上单调递减,
2 2
v x v 1 1 1所以 max ,所以 a
1
a ,即 的取值范围是 , ..................................12分 2 2e 2e 2e
高二期中考试 数学答案 第 10页 共 10页
数学试题
考试时间:120 分钟 满分:150 分
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上写在本试卷上无效.
一、单选题:本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有一项
符合题目要求.
1 2.已知集合 A x x 9 , B x | 1 x 5, x N ,则 A B ( )
A. 1,3 B. 0,5 C. 1,2 D. 0,1,2
2.若复数 z满足 i z 3 4i,则 z ( )
A.1 B.5 C.7 D.25
3.设 a R,则“ a 1”是“直线 l1: ax 2y 4 0与直线 l2: x a 1 y 2 0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.记等差数列 an 的前 n项和为 Sn,若 S11 44,则 a4 a6 a8 ( )
A.12 B.13 C.14 D.15
1
5. 函数 f (x) x3 4x2 9x 6在区间[-1,2]上的最小值为( )
3
56 20 4
A. B. C. D. 3
3 3 3
6. 已知圆的方程为 x2 y2 6x 8y 0,设该圆过点 3,5 的最长弦和最短弦分别为 AC和 BD,
则四边形 ABCD的面积为( )
A.10 6 B. 20 6 C.30 6 D. 40 6
x27 y
2
.已知 F为双曲线C : 2 2 1(a 0,b 0)的左焦点,直线 l经过点 F,若点 A(a,0),B(0,b)a b
关于直线 l对称,则双曲线 C的离心率为( )
A 3 1 B 2 1. . C. 3+1 D. 2+1
2 2
ln3
8 a 10.已知 ln10,b 2 2 , c ,则( )
20 e3 3
A. a c b B. c b a C.b a c D.b
二、多选题:本题共 4 小题,每小题 5 分,共 20 分在每小题给出的选项中,有多项符合题目要
求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 2 分.
9.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”、“乐”、“射”、“御”、
“书”、“数”六门体验课程,每周一门,连续开设六周,则下列说法正确的是( )
A.某学生从中选 2门课程学习,共有 15种选法
B.课程“乐”“射”排在不相邻的两周,共有 240种排法
C.课程“御”“书”“数”排在相邻的三周,共有 144种排法
D.课程“礼”不排在第一周,也不排在最后一周,共有 480种排法
10.已知等比数列{an}的公比为q,前n项积为Tn,若a1 128,且T7 T8 ,则下列命题正确的是( )
A. a8 1 B.当且仅当 n 8时,Tn 取得最大值
1
C q D. a a a *.
2 1 2 n
a1 a2 a15 n n N ,n 15
11 2.已知抛物线C : x 2py p 0 的焦点为 F,点 A 2,1 在 C上,P为 C上的一个动点,则( )
A.C的准线方程为 x= 1
B.若M 0,3 ,则 PM 的最小值为2 2
C.若M 3,5 ,则△PMF的周长的最小值为 11
D.在 x轴上存在点 E,使得 PEF为钝角
1
12. 已知函数 f x e2x , g x lnx 分别与直线 y a交于点 A,B,则下列说法正确的( )
2
A. AB
1
的最小值为 ln2 1
2
B. a R,使得曲线 y f x 在点 A处的切线与曲线 y g x 在点 B处的切线平行
C.函数 y f x g x 的最小值小于 2
D.若 2 x e f x 3 2g x ,则 x e
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
( x 113 5.在代数式 2 ) 的展开式中,常数项为_____________.x
2x 1
14.曲线 y 在点 ( 1, 3)处的切线方程为__________.
x 2
15.某班宣传小组有 3名男生和 2名女生.现从这 5名同学中挑选 2人参加小剧场演出,在已知
抽取到有男生的条件下,2名都是男生的概率为___________.
16.已知函数 f x x ln x ae x( e为自然对数的底数)有两个极值点,则实数 a的取值范围是
___________.
高二期中考试 数学试卷 第 2页 共 4页
四、解答题:本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分 10分)某校为增强学生的环保意识,普及环保知识,在全校范围内组织了一
次有关环保知识的竞赛. 现从参赛的所有学生中,随机抽取 200人的成绩(满分为100分)
作为样本,得到成绩的频率分布直方图如图所示.
(1)求频率分布直方图中 a的值,并估计该校此次环保知识竞赛成绩的第50百分位数;
(2)在该样本中,若采用分层抽样的方法,从成绩低于70分的学生中随机抽取6人,查看
他们的答题情况,再从这6人中随机抽取 2人进行调查分析,求这 2人中至少有1人成绩在
60,70 内的概率.
18.(本小题满分 12分)如图所示,在 ABC中, A, B, C的对边分别为 a,b,c,已知
2bsin AcosB a sin B 0, a 1, c 2 .
(1)求b和sinC;
(2 BD 3)如图,设 D为 AC边上一点, ,求 ABD的面积.CD 7
19.(本小题满分 12分)在数列 an 中,已知 a1 2, an 1 3an 2 n N* .
(1)证明:数列 an 1 为等比数列;
b 3
n 499
(2)记 n ,数列 bn 的前 n项和为 Sn,求使得 S 成立的整数n的最大值.ana nn 1 2000
高二期中考试 数学试卷 第 3页 共 4页
20.(本小题满分 12分)如图,在多面体 ABCDEF 中,四边形 ABCD是边长为 4的菱形,
BCD 60 , AC与 BD交于点O,平面FBC 平面 ABCD, EF // AB, FB FC,且
EF 2 .
(1)求证:OE 平面 ABCD;
(2)若 AE FC,点Q为 AE的中点,求二面角Q BC A的余弦值.
2 2
21.(本小题满分 12分)已知椭圆C : x y2 2 1(a b 0),四点 P1(0,2),P2 (1,1),P3( 2,1),a b
P4 ( 2,1)恰有三点在C上.
(1)求C的方程;
2 x2 y2
4
( )若圆 的切线 l与C交于点 A,B,证明:OA OB .
3
2ae2x22.(本小题满分 12分)已知函数 f x ,a 0 .
x
(1)讨论函数 f x 的单调性;
(2)若 ln x xf x lna恒成立,求实数 a的取值范围.
高二期中考试 数学试卷 第 4页 共 4页
南宁名校 2022~2023学年度下学期高二期中考试
数学试题参考答案
1.D【详解】集合 A x | x2 9 x | 3 x 3 ,集合 B x | 1 x 5, x N 0,1,2,3,4 ,
则 A B 0,1, 2 ,故选:D.
z 3 4i 3 4i i 2.B【详解】由题意有 4 3ii i i ,故 | z | 4
2 3 2 5.故选:B.
3.C【详解】解:当 a 1时, l1: x 2y 4 0 l x 2y 2 0
1 2 4
, 2: , ,可得两直线1 2 2
平行;若l1与l
a 2 4
2平行,则 ,解得a 1或a 2(舍 ),故为充要条件,故选:C.1 a 1 2
4.A【详解】根据数列 a 11 a a n 为等差数列,则 S 1 1111 11a6 44,所以 a6 4,所以2
a4 a6 a8 3a6 12,故选:A.
1
5.C【详解】由 f (x) x3 4x2 9x 6, x [ 1,2]可得 f (x) x 2 8x 9,令 f (x) 0,解得
3
x 1,当 1 x 1, f (x) 0, f (x)单调递减;当1 x 2, f (x) 0, f (x)单调递增,所以 f (x)
1 4
的极小值,也为最小值为 f (1) 4 9 6 ,故选:C
3 3
6.B【详解】解:圆心坐标是 3, 4 ,半径是 5,圆心到点 3,5 的距离为 1.
所以点 3,5 在圆内,最长弦为圆的直径。由垂径定理得:最短弦 BD和最长弦(即圆的直径)
AC垂直,故最短弦的长为2 52 12 4 6 ,最长弦即直径,即 AC 10,
1
所以四边形 ABCD的面积为 AC BD
1
10 4 6 20 6.故选:B.
2 2
7.C【详解】解法一:由点 A(a,0),B(0,b)关于直线 l对称,
a bl
b
可得直线 为线段 AB的垂直平分线,线段 AB的中点的坐标为 , ,直线 AB的斜率为 ,
2 2 a
b a a 2 2
可得直线 l的方程为 y- x
1 b 1 b
2 b 2
,令 y=0,可得 x= a ,由题意可得-c a ,
2 2a 2 2a
c
即有 a(a+2c)=b2=c2-a2,即 c2-2ac-2a2=0,由 e= ,可得 e2-2e-2=0,
a
解得 e=1 3 ( e=1 3舍去),故选:C.
高二期中考试 数学答案 第 1页 共 10页
解法二:由点 A(a,0),B(0,b)关于直线 l对称,可知 AF BF ,即 a c b2 c2 ,
两边平方,并结合b2 c2 a2,整理可得 c2-2ac-2a2=0,下同解法一.
f x ln x 1 ln x8.C【详解】设函数 x e ,则 f x 2 0,则 f x 在 e, 上是减函数,x x
又 e 3 10 e3,则 f 3 f 10 f e3 ,
f 10 ln 10 10
3 ln 3
又因为 ln10 a f e3 ln e 3 2 2, , f 3 c ,10 20 e3 e3 e3 3
所以 f 3 f 10 f e3 b,即b a c.故选:C.
9.ACD 2【详解】对于 A,从六门课程中选两门的不同选法有C6 15种,A正确;
对于 B 4 2,先排“礼”、“御”、“书”、“数”,再用插空法排“乐”“射”,不同排法共有 A4 A5 480种,
B错误;对于 C,“御”“书”“数”排在相邻的三周,可将“御”“书”“数”视为一个元素,不同排法
A3A4共有 3 4 144种,C正确;对于 D,从中间四周中任取一周排“礼”,再排其它五门体验课程
共有 4A55 480种,D正确.故选:ACD.
10.ACD【详解】因为T7 T8 ,所以a8 1,故 A正确;
n 1 7 1 1
又 a8 a1q ,即 q ,解得 q ,故 C正确;128 2
由 q
1
知等比数列{an}为递减数列,且a8 1,故Tn取得最大值为T7 T8,故 B错误;2
n (n 1) n(n 15)
因为 a a a a nq1 2 n 11 2 n 1 (q
7 )nq 2 q 2 ,
(14 n)(15 n) n2 15n n(n 15)
a a a a 15 nq1 2 14 n (q 7 )15 n 2 2 21 2 15 n 1 q q q
*
所以 a1 a2 an a1 a2 a15 n n N ,n 15 成立,故 D正确. 故选:ACD
11.BC【详解】A选项:因为点 A 2,1 在抛物线C : x2 2 py上,所以 22 2 p,解得 p 2,
所以抛物线 C的方程为 x2 4y,所以 C的准线方程为 y 1,故 A错误;
B 2选项:设点 P(x0,y0 ), y0 0,则 x0 4y0 ),
因为M 0,3 2,所以 PM x20 y0 3
2 y20 2y0 9 y
2
0 1 8 8,
高二期中考试 数学答案 第 2页 共 10页
当且仅当 y0 1时等号成立,所以 PM 2 2min ,故 B正确;
C选项:过点 P作PN垂直于 C的准线,垂足为 N,连接 MN,则 PN PF ,
易知 F 0,1 ,M 3,5 2,所以 MF 32 5 1 5,
所以△PMF 的周长为 MF MP PF MF MP PN MF MN 5 6 11,
当且仅当 M,P,N三点共线时等号成立,
所以△PMF 的周长的最小值为 11,故 C正确;
D选项:设 E t, 0 ,则 EF t,1 , EP x0 t, y0 ,
所以 EF EP t x0 t y 20 t x0t y0,
2
因为点 P(x0,y0 )在 C上,所以 x
2
0 4y
x
0 ),即 y 00 ,4
2 2
所以 EF EP t 2 x 0t
x
0 t
x
0 0,4 2
EF EP
所以 cos PEF 0 ,故 PEF不可能为钝角,故 D错误.EF EP
故选:BC.
1
12 AB 2x. 【详解】对于 A项,设 A x1,a , B x2 ,a ,则 f x1 e 1 a, x1 lna,2
1 a 1 a
1
1
又因为 g x2 lnx2 a, x 2 ,所以 AB x2 x1 e 2 lna a 0 ,2 2 e 2
a 1 a 1
设 a =e 2 1 ln a a 0 ,所以 a =e 2 1 a 0 ,
2 2a
a 1 1 1
又因为 a =e 2 1 在 0, 0单调递增,且 =e 1 0 ,当 a 0, , a 0;,2a 2 2
a 1当 , , a
1 1
0 a 0, 所以 在 上单调递减,在 , 单调递增,
2 2 2
a 1 1 1 1所以 e0 ln 1 ln 2
1
,所以 AB 的最小值为 ln2 1,故 A正确.
2 2 2 2 2
对于 B项,函数 f x e2x A x ,a f x 2e2x在点 1 处切线的斜率为 11 ,
又因为 x
1
1 lna
2x
,所以函数 f x e 在点 A x1,a 处切线的斜率为2
高二期中考试 数学答案 第 3页 共 10页
2 1 ln a
f x 2e2x11 2e 2 2a,
1
函数 g x lnx 1 在点 B x ,a 处切线的斜率为 g x ,
2 2 2 x2
a 1 1 1 1又因为 x e 2 ,所以函数 g x lnx 在点 B x2 ,a 处切线的斜率为 g x2 2 2 x2 a 1 ,e 2
要使曲线 y f x 在点A处的切线与曲线 y g x 在点 B处的切线平行,即
1 1
f x1 g x2 2a
1 a
,所以 a 1 有解,即方程
a
2a e 2 1 0 有根.即函数 h a 2a e 2 1有e 2
零点,
a 1 h 1 1
1 1
又因为当 , 2 e 2 2 1 0 ,故 B正确.2 2 2
C y f x g x e2x对于 项, ln x 1 1 2x,因为 y 2e 在 0, 上单调递增,
2 x
2 1
2 1
x 1 y 2e 1 2e 2 2 e 1 0当 时, ,
2
2
2 1 1
x 1 y 2e
4 1 2
当 时, 1 2e 4 2 e 2 0,
4
4
x 1 , 1 2x
1 1
则存在 0
2x0
0 ,使得 2e 0,即 e , ln 2 2x0 ln x0 ,
4 2 x0 2x0
当 x 0, x0 时, y 0; x x0 , 时, y 0,
y y e2x ln x 1 1 2x ln 2 1所以 min x x 0 0 0 2
1 2x ln 2 1 2 ln 2 1 0 0 2 2x ,0 2 2x0 2 2
1
(由于 x ,故等号取不到),
2
又因为 2
1
ln 2 2,函数 y f x g x 的最小值大于 2,故 C错误;
2
对于 D项,不等式2 x e f x 3 2g x 2x化简后变为: x e e ln x 1 0,
当 x 0,e 时, x e 0, ln x 1 0,e 2x 0 , x e e2x ln x 1 0,
当 x e, 时, x e>0, ln x 1 0,e 2x 0 , x e e2x ln x 1 0,
所以 2 x e f x 3 2g x ,则 x e,故 D错误.
高二期中考试 数学答案 第 4页 共 10页
5 1 5 r r 5 5r
13.-5 x 1 1 r【详解】 2 的展开式的通项为:T C
r 2
r 1 5 x 2 C
r 2
5x 1
x x
5 5r 5
令 0 1 1 ,解得 r 1,所以T 12 1 C5 1 5, x 2 的展开式中的常数项为 5 .2 x
14.5x y 2 0【详解】由题,当 x= 1时, y= 3,故点在曲线上.
2 x 2 2x 1 5
求导得: y ,所以 y | 5 .x 2 2 x 2 2 x 1
故切线方程为5x y 2 0.故答案为:5x y 2 0.
1
15. 【详解】设事件 A表示“有男生”,事件 B表示“两名都是男生”,
3
3
2 2 P AB
则 P(A) 1
C
2
9 C 3 1
3 12 , P(AB) ,故 P B A 10 .故答案为: .C5 10 C25 10 P A 9 3 3
10
16.0
1
a 【详解】 f x 1 ln x aex,因为函数 f x x ln x ae x( e为自然对数的底数)
e
有两个极值点,所以1 ln x aex 0在 0, 上有两个不等实根,
a 1 ln x 1 ln x x 在 0, 上有两个不等实根,令 g x ,e ex
1
1 ln x
g x x ,当 0 x 1时, g (x) 0,当 x 1时, g (x) 0,
ex
1
所以当 x 1时, f x 的最大值为 ;
e
当 x 0时, g x ,当 x 时, f x 0,
1
如图所示:所以实数 a的取值范围是0 a .
e
0 a 1故答案为:
e
4
17.(1)a 0.025,第50百分位数为75.6 (2)
5
解:(1)由频率分布直方图可得, 0.006 0.012 0.018 2 0.021 a 10 1,..............1分
则 a 0.025, ........................................................................2分
前 3组的频率和为 0.006 0.012 0.018 10 0.36,第 4组频率为0.25,所以第50百分位数
高二期中考试 数学答案 第 5页 共 10页
位于第 4组 70,80 内,记第 50百分位数为 x,.......................................................................3分
x 70 0.5 0.36
则 ,解得 x 75.6,即第 50百分位数为75.6;....................................5分
10 0.25
(2)由频率分布直方图可知,成绩在 40,50 , 50,60 , 60,70 内的频率分别为0.06,0.12,0.18,
采用分层抽样的方法从样本中抽取的 6人,成绩在 40,50 内的有 1人,记为A,成绩在 50,60
内的有 2人,记为 B1 B2,成绩在 60,70 内的有 3人,记为C1 C2 C3,.................................6分
则从成绩在 40,70 内的 6人随机抽取 2人,共有:
AB1 AB2 AC1 AC2 AC3 B1C1 B1C2 B1C3 B2C1 B2C2 B2C3 C1C2 C1C3 C2C3 B1B2,共有 15种,
2人中至少有 1人成绩在 60,70 内,共有:
AC1 AC2 AC3 B1C1 B1C2 B1C3 B2C1 B2C2 B2C3 C1C2 C1C3 C2C3,有 12种,............................8分
12 4
记事件 A “ 2人中至少有 1人成绩在 60,70 内”,则 P A .....................................10分
15 5
18. 1 a b c解( )因为 2bsin AcosB asin B 0 ,所以在 ABC中,由正弦定理 ,
sin A sin B sinC
得 2sin B sin Acos B sin Asin B 0,因为 sin Asin B 0 ,所以 2cosB 1 0,
cos B 1 2 所以 ,又0 B ,所以 B ,....................................3分
2 3
1
由余弦定理得,b2 a2 c2 2ac cosB 1 4 2 1 2
7,所以 ,
2
b 7
c b
在 ABC中,由正弦定理 ,
sinC sin B
2sin 2
所以 sinC
c sin B
3 21 ;....................................6分b
7 7
BD sinC
(2)在△ABD中,由正弦定理得, ,
CD sin CBD
BD 3 sinC 3 21
因为 ,所以 ,因为 sinC ,所以 sin CBD 1,
CD 7 sin CBD 7 7
而 CBD 0, ,所以 CBD ,....................................8分
2
BD 3 1
由 ,设 BD 3t , CD 7t,所以 ( 3t)2 12 ( 7t)2,所以 t 3,所以 BD ,
CD 7 2 2
高二期中考试 数学答案 第 6页 共 10页
2
因为 ABD ABC DBC ,....................................10分
3 2 6
所以 S
1
ABD AB BD sin ABD
1 3 1 3
2 2
.....................................12分
2 2 2 4
a 1 3 a 1
19.解(1)由 an 1 3an 2,得 an 1 1 3 a 1 n 1 nn , 3,又a 1 3,an 1 an 1 1
故数列 an 1 是以3为首项,3为公比的等比数列;....................................5分
n
2 a 1 3n a 3n b
3 1 1 1
( ) n ,故 n 1,故 n 3n 1 3n 1 1 2 3n 1 3n 1 1 ,......................8分
S 1 1 1 1 1 1 1 1 1 1 1 1n 1 2 2 3
2 3 1 3 1 2 3 1 3 1 2 3n 1 3n 1
n 1 ,...........10分 1 4 2 3 1
S 499 1 1 1 499n ,即 n 1 ,即3n 1 1001,36 1001 37 ,故 n 5,2000 4 2 3 1 2000
故使得 S
499
n 成立的最大整数为5 .....................................12分2000
20.(1)证明:如图,取 BC中点G,连接 FG,OG,
因为 FB FC,所以 FG BC,
又因为平面FBC 平面 ABCD,平面 FBC 平面 ABCD BC, FG 平面FBC,
所以 FG 平面 ABCD, O,G分别为 AC,BC
1
中点,所以OG∥ AB,OG AB .
2
1
因为EF AB,EF / /AB, EF / /OG,EF OG
2
所以四边形EFGO为平行四边形,所以OE∥FG,所以OE 平面 ABCD ..........................6分
(2)如图,以 AC所在直线为 x轴, BD所在直线为 y轴,OE所在直线为 z轴建立空间坐标
系,设OE 0,0,c , (c 0)
A 2 3,0,0 ,B 0, 2,0 ,C 2 3,0,0 ,Q c 3,0,
2
F 3,1,c ,CF 3,1,c ,CF AE 0, c 6 6,Q 3,0,
2
设平面QBC的法向量 v x, y, z ,BC 2 3, 2,0 ,BQ 3, 2,
6
2
高二期中考试 数学答案 第 7页 共 10页
v
BQ 0
2 3x 2y 0
则
即 6 ,则 v 1, 3, 3 2 .
v BC 0 3x 2y z 0 2
设平面 ABC的法向量 n 0,0,1 ,设二面角Q BC A的平面角为 , 为锐
角,....................................10分
n v 3 11 3 11
所以 cos .二面角Q BC A的余弦值 .....................................12分n v 11 11
2 2
21.(1) x y 1; (2)证明见解析
4 2
【详解】(1)由 P y3 ,P4 两点关于 轴对称,可得C经过 P3 ,P4 两点.
P2与P3的纵坐标相同,且都位于第一象限,不可能都在C上,所以 P2不在C上,
b 2,
a 2, C x
2 y2
则 2 1 解得 故 的方程为 1.....................................4分
2 2 1, b 2. 4 2 a b
2 2 3( )证明:当切线 l的斜率不存在时,得 l : x .
3
2 3 2 3 2 3 2 3
当 l : x 2 3 时,可得 A
3
,
3 3
,B , .
3 3
OA OB 2 3 2 3 2 3 2 3 0,则OA OB .....................................6分
3 3 3 3
当 l : x 2 3 时,同理可证.
3
当切线 l的斜率存在时,设 l : y kx m .
l x2 y2 4
m 2 3 2 2
因为 与圆 相切,所以圆心 0,0 到 l的距离为 ,即3m 4 k 1 .
3 k 2 1 3
y kx m,
联立 x2 y2 得 2k 2 1 x2 4kmx 2m2 4 0 .
1, 4 2
A x , y ,B x , y x x 4km
2
设 1 1 2 2 ,则 1 2 2 , x x
2m 4
1 2 2 .....................................8分1 2k 1 2k
OA OB x 2 21x2 y1y2 x1x2 (kx1 m)(kx2 m) (k 1)x1x2 km(x1 x2 ) m
高二期中考试 数学答案 第 8页 共 10页
k 2 1 2m2 4 4k 2m2 4k 2 3m2 4
m2
1 2k 2 1 2k 2 1 2k 2
2 2 由3m 4 k 1 ,得OA OB 0,则OA OB .
x2 y2 4综上,若圆 的切线 l与C交于点 A,B,则OA OB .....................................12分
3
1
22. (1)见解析; (2) ,
2e
2ae2 x 4ae2 x 2 x 2 x1 f x x 2ae 2ae 2x 1解:( )因为 ,所以 f x .
x x2 x2
1 1
当a 0时,由 f (x) 0,得 x ,由 f x 0,得 x ,且 x 0,
2 2
故 f x 1 1 的单调递增区间为 , ,单调递减区间为 ,0 , 0, ;
2 2
当 a<0时,由 f (x) 0 x 1,得 ,且 x 0,由 f x 0 x 1,得 ,
2 2
故 f x 1 1 的单调递增区间为 ,0 , 0, ,单调递减区间为2 , . 2
a 0 f x 1 1 综上,当 时, 的单调递增区间为 , 2 ,单调递减区间为 ,0 , 0, ; 2
当 a<0时, f x 的单调递增区间为 ,0 , 0,
1
2
,
1 , 单调递减区间为 .....................................5分
2
(2)易知 x 0, a 0 .
2x x
由 ln x xf x lna,可得 2ae ln x ln a ln ,
a
x
2xe2x x
ln
所以 ln
x
恒成立,即 2xe2x e a ln x恒成立.
a a a
设u x xex x 0 u x x 1 ex, ,则 0,所以 u x 在 0, 上单调递增.
x
当 x 0时,u x 0 ln,所以2xe2x e a ln x x恒成立等价于2x ≥ ln 恒成立,
a a
x
即a ≥ 对 x 0, 恒成立.
e2x
v x x 1 2x设 , x 0, v x .
e2x e2x
x 0, 1 当 时, v x 0
1
;当 x , 时, v x 0 .
2 2
高二期中考试 数学答案 第 9页 共 10页
所以 v x 在 0,
1 1
上单调递增,在 , 上单调递减,
2 2
v x v 1 1 1所以 max ,所以 a
1
a ,即 的取值范围是 , ..................................12分 2 2e 2e 2e
高二期中考试 数学答案 第 10页 共 10页
同课章节目录
