2022-2023学年北师大版八年级下册数学 第一章三角形的证明自我达标训练(无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级下册数学 第一章三角形的证明自我达标训练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 20:39:06 | ||
图片预览

文档简介
第一章三角形的证明
一、选择题。
1.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
2.如图,已知△ABC中,∠B=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为( )
A.100° B.105° C.115° D.120°
3.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
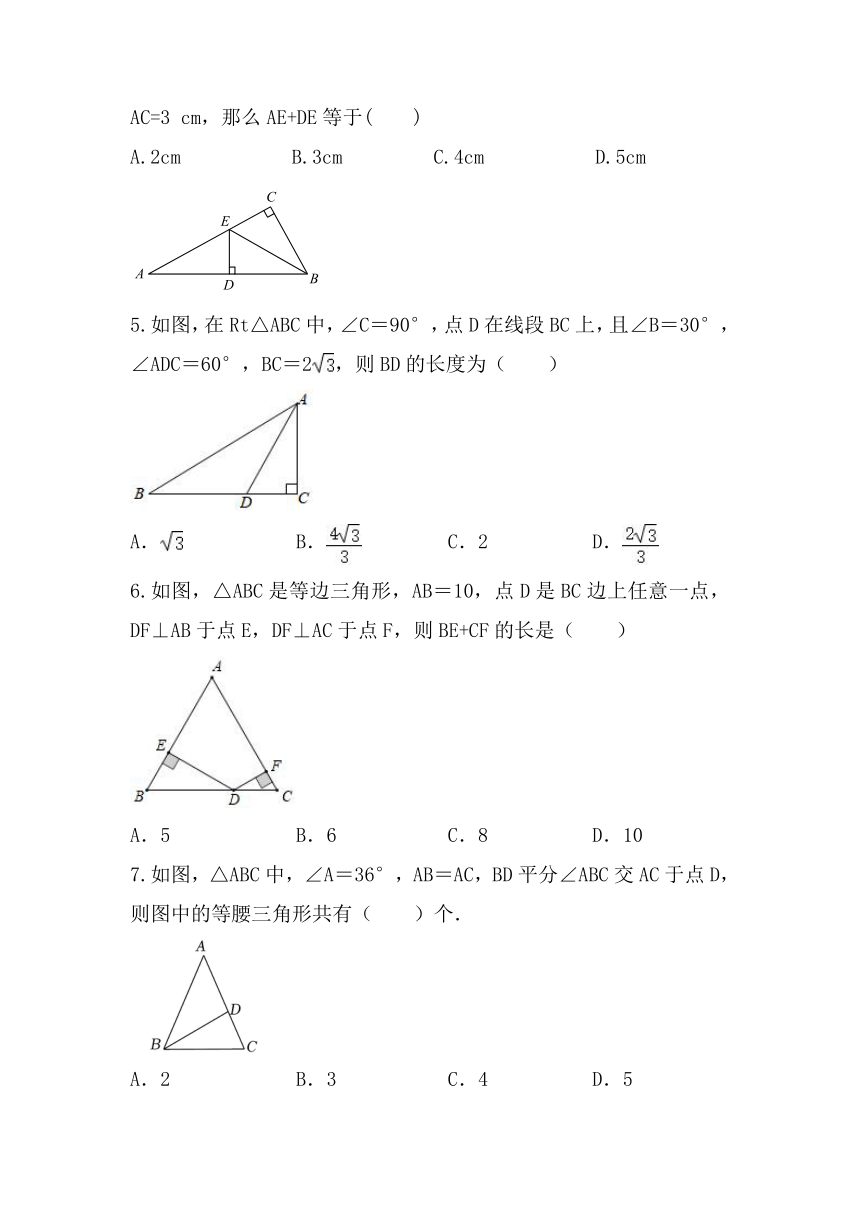
4.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=2,则BD的长度为( )
A. B. C.2 D.
6.如图,△ABC是等边三角形,AB=10,点D是BC边上任意一点,DF⊥AB于点E,DF⊥AC于点F,则BE+CF的长是( )
A.5 B.6 C.8 D.10
7.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有( )个.
A.2 B.3 C.4 D.5
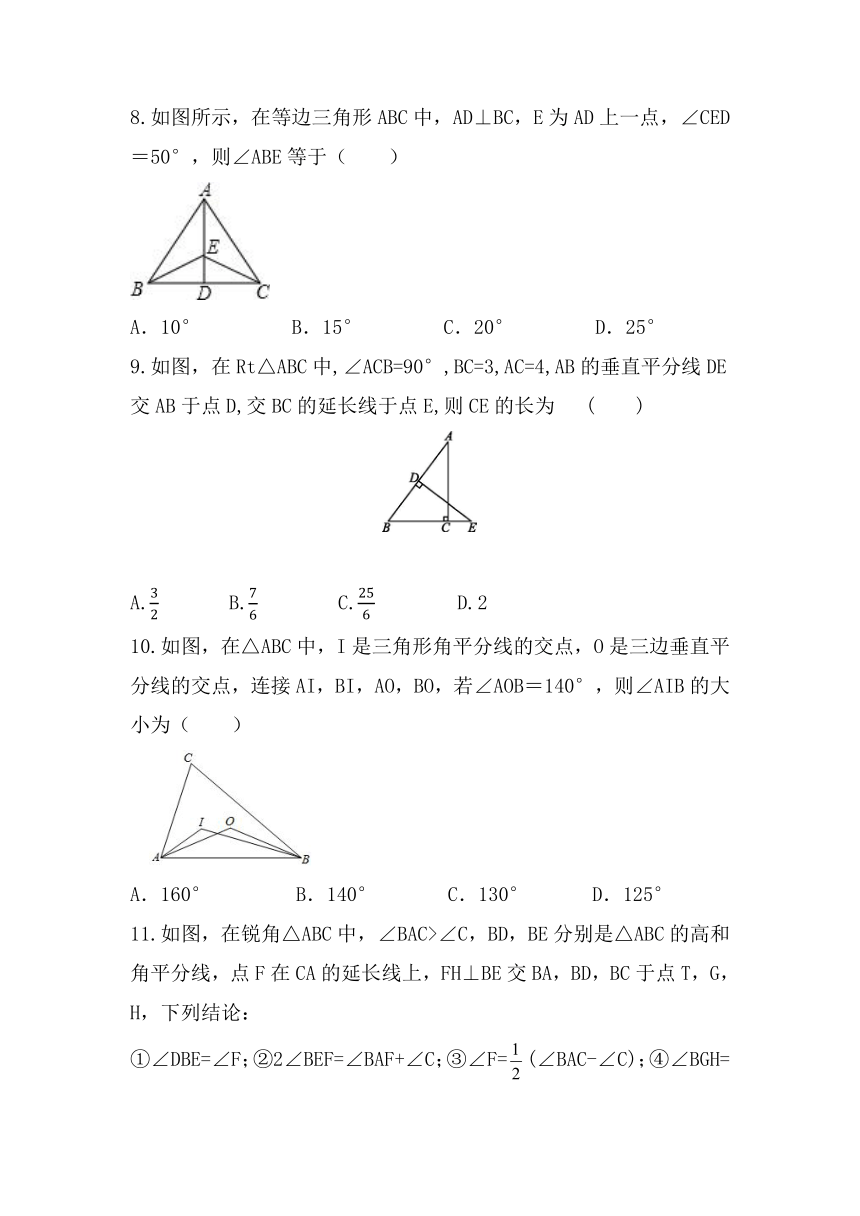
8.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
9.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交BC的延长线于点E,则CE的长为 ( )
A. B. C. D.2
10.如图,在△ABC中,I是三角形角平分线的交点,O是三边垂直平分线的交点,连接AI,BI,AO,BO,若∠AOB=140°,则∠AIB的大小为( )
A.160° B.140° C.130° D.125°
11.如图,在锐角△ABC中,∠BAC>∠C,BD,BE分别是△ABC的高和角平分线,点F在CA的延长线上,FH⊥BE交BA,BD,BC于点T,G,H,下列结论:
①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC-∠C);④∠BGH=∠ABD+∠EBH.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题。
1.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE= .
2.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
3.如图,在边长为 的等边三角形 中, 是 边上的高,点 , 是 上的两点,则图中阴影部分的面积是 .
4.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于点E,交BC于点D, BD=8,则AC= .
5.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=_______.
6.如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有 个.
三、解答题。
1.如图所示,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,延长CE到点G,使CG=AB.若∠BCE=45°.求证:AB垂直平分GF.
2.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
3.如图,在等边△ABC中,点D在边BC上,过点D作DE∥AB交AC于点E,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)求证:DC=CF.
4.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
(1)求∠A、∠ABC的度数;
(2)连接CE,且CE=AB,求证:△BCE是等边三角形.
5.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC,BC于点M、N.
(1)如图1,若∠BAC=112°,求∠EAN的度数;
(2)如图2,若∠BAC=82°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
一、选择题。
1.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
2.如图,已知△ABC中,∠B=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为( )
A.100° B.105° C.115° D.120°
3.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
4.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=2,则BD的长度为( )
A. B. C.2 D.
6.如图,△ABC是等边三角形,AB=10,点D是BC边上任意一点,DF⊥AB于点E,DF⊥AC于点F,则BE+CF的长是( )
A.5 B.6 C.8 D.10
7.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有( )个.
A.2 B.3 C.4 D.5
8.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
9.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交BC的延长线于点E,则CE的长为 ( )
A. B. C. D.2
10.如图,在△ABC中,I是三角形角平分线的交点,O是三边垂直平分线的交点,连接AI,BI,AO,BO,若∠AOB=140°,则∠AIB的大小为( )
A.160° B.140° C.130° D.125°
11.如图,在锐角△ABC中,∠BAC>∠C,BD,BE分别是△ABC的高和角平分线,点F在CA的延长线上,FH⊥BE交BA,BD,BC于点T,G,H,下列结论:
①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC-∠C);④∠BGH=∠ABD+∠EBH.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题。
1.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE= .
2.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
3.如图,在边长为 的等边三角形 中, 是 边上的高,点 , 是 上的两点,则图中阴影部分的面积是 .
4.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于点E,交BC于点D, BD=8,则AC= .
5.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=_______.
6.如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有 个.
三、解答题。
1.如图所示,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,延长CE到点G,使CG=AB.若∠BCE=45°.求证:AB垂直平分GF.
2.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
3.如图,在等边△ABC中,点D在边BC上,过点D作DE∥AB交AC于点E,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)求证:DC=CF.
4.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
(1)求∠A、∠ABC的度数;
(2)连接CE,且CE=AB,求证:△BCE是等边三角形.
5.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC,BC于点M、N.
(1)如图1,若∠BAC=112°,求∠EAN的度数;
(2)如图2,若∠BAC=82°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
