2021-2022学年湖北省七年级下学期人教版数学第十章数据的收集、整理与描述练习题期末试题选编(含解析)
文档属性
| 名称 | 2021-2022学年湖北省七年级下学期人教版数学第十章数据的收集、整理与描述练习题期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 895.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 20:52:43 | ||
图片预览




文档简介
第十章:数据的收集、整理与描述
一、单选题
1.(2022春·湖北咸宁·七年级统考期末)下列调查中,适合用全面调查方式的是( )
A.对全国中学生心理健康现状的调查 B.对某航班旅客上飞机前的安检
C.了解一批签字笔的使用寿命 D.对冷饮市场上冰淇淋质量情况的调查
2.(2022春·湖北武汉·七年级统考期末)要调查下列问题,适合采用全面调查(普查)的是( )
A.中央电视台《开学第一课》的收视率
B.某城市居民6月份人均网上购物的次数
C.即将发射的气象卫星的零部件质量
D.某品牌新能源汽车的最大续航里程
3.(2022春·湖北孝感·七年级统考期末)下列调查中,适宜采用抽样调查的是( )
A.调查一批从疫情中高风险地区来并人员的核酸检测结果
B.调查奥运会马拉松比赛运动员兴奋剂的使用情况
C.调查某批中性笔的使用寿命
D.调查神舟十三号载人飞船各零部件的质量
4.(2022春·湖北恩施·七年级统考期末)为了了解我市6000名学生参加的初中毕业会考数学考试的成绩情况,从中抽取了200名考生的成绩进行统计,在这个问题中,下列说法:(1)这6000名学生的数学会考成绩的全体是总体;(2)每个考生是个体;(3)200名考生是总体的一个样本;(4)样本容量是200,其中说法正确的有( )
A.4个 B.3个 C.2个 D.l个
5.(2022春·湖北襄阳·七年级统考期末)下列调查方式,你认为最合适的是( )
A.为了解全市学生每天参加体育锻炼的时间,采取抽样调查方式
B.襄阳机场对旅客进行登机前安检,采用抽样调查方式
C.为了调查2022年度湖北省人均收入情况,调查省会城市武汉的人均收入
D.要调查一批灯管的使用寿命,采用全面调查的方式
6.(2022春·湖北随州·七年级统考期末)甲、乙、丙三个小组生产帐蓬,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.如图是描述三个小组一天生产帐蓬情况的统计图,从中可以得出人数最多的小组是( )
A.甲组 B.乙组 C.丙组 D.乙、丙两组
7.(2022春·湖北孝感·七年级统考期末)如图所示的两个统计图,女生人数多的学校是( )
A.甲校 B.乙校
C.甲、乙两校女生人数一样多 D.无法确定
8.(2022春·湖北随州·七年级统考期末)2022年北京冬奥会期间,为了记录某一运动员的体温变化情况,应选择的统计图是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
9.(2022春·湖北十堰·七年级统考期末)一个容量为80的样本中,最大数是141,最小数是50,取组距为10,可以分成( )组
A.10组 B.9组 C.8组 D.7组
二、填空题
10.(2022春·湖北襄阳·七年级统考期末)为了考察我市5000名七年级学生数学知识与能力测试的成绩,从中抽取100份试卷进行分析,那么样本容量是_____.
11.(2022春·湖北黄石·七年级统考期末)2020年是抗美援朝胜利70周年,为了解初中生对抗美援朝历史的知晓情况,某校课外兴趣小组在本校2400名学生中展开了调查,随机抽查了200名学生,其中“非常了解”的学生有90名,则可估计该校学生对抗美援朝历史“非常了解”的学生有________名.
12.(2022春·湖北随州·七年级统考期末)在扇形统计图中,有两个扇形的圆心角度数之比为3:4,且较小扇形表示24本课本书,则较大扇形表示___本课本书
13.(2022春·湖北荆门·七年级统考期末)王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码 S M L XL XXL XXL
频率 0.05 0.1 0.2 0.325 0.3 0.025
则该班学生所穿校服尺码为“L”的人数有________个.
14.(2022春·湖北武汉·七年级统考期末)在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是______;
类型 健康 亚健康 不健康
数据(人) 32 7 1
三、解答题
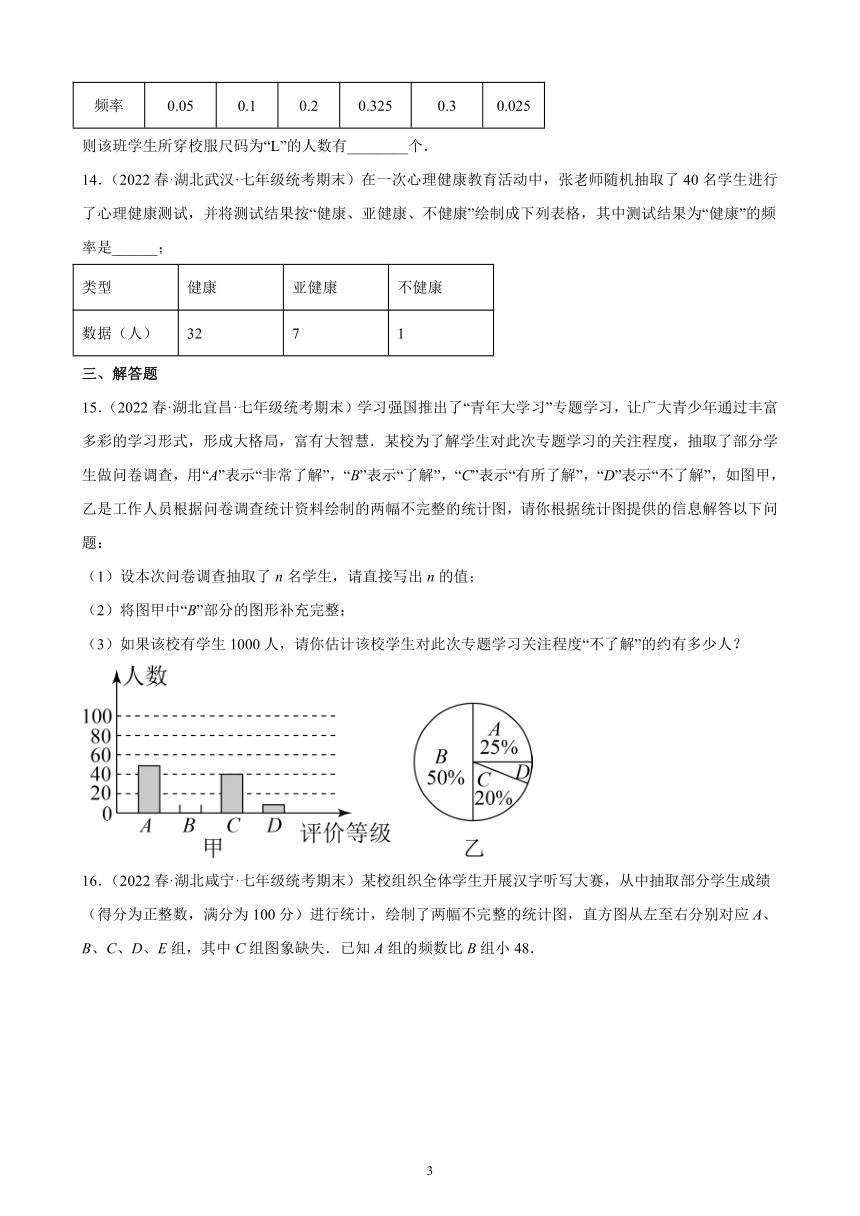
15.(2022春·湖北宜昌·七年级统考期末)学习强国推出了“青年大学习”专题学习,让广大青少年通过丰富多彩的学习形式,形成大格局,富有大智慧.某校为了解学生对此次专题学习的关注程度,抽取了部分学生做问卷调查,用“A”表示“非常了解”,“B”表示“了解”,“C”表示“有所了解”,“D”表示“不了解”,如图甲,乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)设本次问卷调查抽取了n名学生,请直接写出n的值;
(2)将图甲中“B”部分的图形补充完整;
(3)如果该校有学生1000人,请你估计该校学生对此次专题学习关注程度“不了解”的约有多少人?
16.(2022春·湖北咸宁·七年级统考期末)某校组织全体学生开展汉字听写大赛,从中抽取部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,直方图从左至右分别对应A、B、C、D、E组,其中C组图象缺失.已知A组的频数比B组小48.
请你根据图中提供的信息解答下列问题:
(1)求频数分布直方图中a、b的值;
(2)扇形图中D部分扇形所对的圆心角的度数为__________;
(3)若80分以上为优秀,全校共有1000名学生,估计成绩优秀的学生有多少名?
17.(2022春·湖北武汉·七年级统考期末)目前“微信”“支付宝”“共享单车”和“网购”给我们的生活带来了很多便利,九年级数学小组在校内对“你最认可的新生事物”进行调查,随机调查了m名学生(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如图所示不完整的统计图.
(1)根据图中信息,求出__________,__________;
(2)请把条形统计图补充完整;
(3)根据抽样调查的结果,请估算在全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的学生共有多少名.
18.(2022春·湖北襄阳·七年级统考期末)某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图.
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图;
(2)求,的值;
(3)求扇形统计图中“书法”所对应扇形的圆心角的度数.
(4)若该校有800名学生,估计选择摄影的有多少人?
19.(2022春·湖北十堰·七年级统考期末)自从新冠肺炎疫情爆发,我国高度重视并采取了强有力的措施进行防控.武汉是疫情最先爆发的地区,为了帮助武汉人民尽快度过难关,某校八年级全体同学参加了捐款活动.现随机抽查了部分同学捐款的情况统计如图所示;
(1)在本次调查中,一共抽查了__________名学生;
(2)请补全条形统计图,并计算在扇形统计图中,“捐款20元”对应的圆心角度数是_________度;
(3)在八年级600名学生中,捐款15元以上(不含15元)的学生估计有多少人?
20.(2022秋·湖北荆州·七年级校考期末)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 名,参加剪纸的学生有 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 %;
(3)若该校七年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
21.(2022秋·湖北黄石·七年级统考期末)实验小学六(1)班全体同学参加一次体育测试后,分为优秀、达标、不达标三级,并画出下面两张统计图.请把统计图补充完整,并根据图中已知信息写出所要计算的相关数据的计算过程.
22.(2022春·湖北鄂州·七年级统考期末)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
频数分布表
组别 步数分组 频数
A 5500≤x<6500 2
B 6500≤x<7500 10
C 7500≤x<8500 m
D 8500≤x<9500 3
E 9500≤x<10500 n
根据以上信息解答下列问题:
(1)填空:__________,__________
(2)请补全频数分布直方图:
(3)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
23.(2022春·湖北荆门·七年级校考期末)某社区从5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成两幅不完整的统计图表:
平均用水a(吨) 3<a≤6 6<a≤9 9<a≤12 12<a≤15 15<a≤18
频数 10 m 36 25 9
频率 0.1 0.2 0.36 n 0.09
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= .
(2)根据题中数据补全频数分布直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
24.(2022春·湖北咸宁·七年级统考期末)为了解某校学生在五一假期阅读的情况,随机抽取了若干名学生进行调查,获得他们的阅读时间(单位:h),并对数据(时间)进行整理、描述.下面给出了部分信息:图1是阅读时间频数分布直方图(数据分成5组:2≤t<4,4≤t<6,6≤t<8,8≤t<10,10≤t≤12),图2是阅读时间扇形统计图.
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)补全图1;
(3)图2中,2≤t<4所在的扇形的圆心角的度数是 ;
(4)已知该校共有1800名学生,估计该校学生在五一假期阅读时间不少于6h的人数.
参考答案:
1.B
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.对全国中学生心理健康现状的调查,适宜采用抽样调查方式,故本选项不合题意;
B.对某航班旅客上飞机前的安检,适宜采用全面调查,故本选项符合题意;
C.了解一批签字笔的使用寿命,适宜采用抽样调查方式,故本选项不合题意;
D.对冷饮市场上冰淇淋质量情况的调查,适宜采用抽样调查方式,故本选项不合题意;
故选:B.
【点睛】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答即可.
【详解】A、中央电视台《开学第--课》 的收视率适合采用抽样调查方式,故不符合题意;
B、某城市居民6月份人均网上购物的次数适合采用抽样调查方式,故不符合题意;
C、即将发射的气象卫星的零部件质量适合采用全面调查方式,故符合题意;
D、某品牌新能源汽车的最大续航里程适合采用抽样调查方式,故不符合题意,
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.调查一批从疫情中高风险地区来并人员的核酸检测结果,适合全面调查,故本选项不符合题意;
B.调查奥运会马拉松比赛运动员兴奋剂的使用情况,适合全面调查,故本选项不符合题意;
C.调查某批中性笔的使用寿命,适宜采用抽样调查,故本选项符合题意;
D.调查神舟十三号载人飞船各零部件的质量,适合全面调查,故本选项不符合题意.
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.C
【详解】解:本题中的个体是每个考生的数学会考成绩,样本是200名考生的数学会考成绩,
故(2)和(3)错误;
总体是我市6000名学生参加的初中毕业会考数学考试的成绩情况,样本容量是200.
所以(1)和(4)正确.
故选C.
5.A
【分析】根据抽样调查和全面调查的区别进行分析判断.抽样调查是通过对样本调查来估计总体特征,其调查结果是近似的;而全面调查得到的结果比较准确.
【详解】解:A. 为了解全市学生每天参加体育锻炼的时间,采取抽样调查方式,该选项符合题意;
B. 襄阳机场对旅客进行登机前安检,应采用全面调查方式,故该选项不符合题意;
C. 为了调查2022年度湖北省人均收入情况,调查省会城市武汉的人均收入,调查样本不具有代表性和广泛性,故该选项不符合题意;
D. 要调查一批灯管的使用寿命,应采用抽样调查的方式,故该选项不符合题意.
故选:A.
【点睛】本题主要考查了抽样调查和全面调查的知识,解题关键在于理清对调查结果的要求.
6.C
【分析】根据统计图数据,分别求出甲、乙、丙三组的男工人与女工人数,然后比较即可.
【详解】解∶甲组男工人的人数为人,女工人的人数为人,
∴甲组的人数18+6=24人;
乙组男工人的人数为人,女工人的人数为人,
∴乙组的人数16+9=25人;
丙组男工人的人数为人,女工人的人数为人,
∴丙组的人数8+18=26人;
∴丙组的人数最多.
故选:C
【点睛】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
7.D
【详解】试题分析:根据题意,结合扇形图的性质,扇形统计图只能得到每部分所占的比例,具体人数不能直接体现,易得答案.
解:根据题意,因不知道甲乙两校学生的总人数,只知道两校女生占的比例,
故无法比较两校女生的人数,
故选D.
8.A
【分析】根据统计图所表示数据的特点进行判定即可.
【详解】解:为了记录某一运动员的体温变化情况,应该选择折线统计图,
故选择A.
【点睛】本题考查条件图的选择,掌握折线统计图所反映的数据的特点是正确判断的关键,折线统计图反映数据的变化情况,突出变化两个字.
9.A
【分析】根据组数=(最大值-最小值)÷组距来计算即可.
【详解】在样本数据中,最大值为何141,最小值为50,它们的差是141-50=91,由于组距为10,那么由于91÷10=9.1,故可以分成10组.
故选:A.
【点睛】本题考查的是组数的计算,属于基础题,只要根据组数的计算公式来计算即可,注意小数部分结果要进位.
10.100
【分析】直接利用样本容量的定义分析得出答案.
【详解】解:∵从中抽取100份试卷进行分析,
∴样本容量是:100.
故答案为:100.
【点睛】本题考查了总体、个体、样本、样本容量的知识,属于基础题,解答本题的关键是分清具体问题中的总体、个体与样本.
11.1080
【分析】根据题意和题目中的数据,可以通过计算估计出该校学生对抗美援朝历史“非常了解”的学生人数.
【详解】解:估计该校学生对抗美援朝历史“非常了解”的学生人数有人,
故答案为:1080.
【点睛】本题主要考查样本估计总体,掌握总体中所占比值与样本中的所占比值近似相等是解题的关键.
12.32
【分析】分别求出较小的占的比例和较大的占的比例,再求出总书数,最后求出较大扇形表示的书数即可.
【详解】∵较小的占的比例为,较大的占的比例为,
∴总书数(本),
∴56-24=32(本)
∴较大的扇形表示32本书.
【点睛】本题是统计图的基础应用题,难度一般,统计图是中考中的常见知识点,学生需要熟练掌握各个统计图的特点.
13.8
【分析】直接用尺码L的频率乘以班级总人数即可求出答案.
【详解】解:由表可知尺码L的频率的0.2,又因为班级总人数为40,
所以该班学生所穿校服尺码为“L”的人数有400.2=8.
故答案是:8.
【点睛】此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.
14.
【分析】根据频率=频数÷总数,即可得到结论.
【详解】解:由题可知,总人数为32+7+1=40人,测试结果为“健康”的有32人,
测试结果为“健康”的频率=;
故结论是:.
【点睛】本题考查频率,掌握频率、频数、总数之间的关系是解题的关键.
15.(1)200名;(2)见解析;(3)50人
【分析】(1)利用C等级人数÷其对应的百分率求解;
(2)用调查总人数×50%得到B等级的人数,从而补充条形统计图;
(3)利用样本估计总体的思想求解
【详解】解:(1)名
∴本次问卷调查抽取了200名学生
(2)B等级对应的人数为:200×50%=100人
补充统计图如下:
(3)1000×(1-50%-20%-25%)=50人
∴该校学生对此次专题学习关注程度“不了解”的约有50人
【点睛】本题考查的是条形统计图和扇形统计图的应用及用样本估计总体,熟知从条形图可以很容易看出数据的大小,便于比较是解答此题的关键.
16.(1)
(2)
(3)470
【分析】(1)根据扇形统计图中的数据和A组的频数比B组小48,可求得调查人数,后计算出a、b的值即可;
(2)根据直方图中的数据,可计算出扇形图中D部分所对的圆心角度数;
(3)根据扇形统计图中的数据,可以计算出优秀学生有多少人.
【详解】(1)解:本次调查人数为:(人)
,
(2)解:由D所占人数最多,得所占人数为:140
则扇形图中D部分扇形所对的圆心角的度数为:
故答案为:
(3)解:由条形统计图,大于80分的在扇形统计图中占
则1000名学生,估计成绩优秀的学生有:1000(人)
【点睛】本题考查频数分布直方图、用样本估计总体、扇形统计图,明确题意,利用数形结合思想时关键.
17.(1)100,35;
(2)见解析;
(3)1350名.
【分析】(1)利用选“共享单车”人数为10,所占百分比为,即可求出m;利用选“网购”所占百分比为,求出选“网购”的人数,进一步可得选“支付宝”的人数,再除以总人数即可求出其所占百分比;
(2)由(1)求出的数据补充条形图即可;
(3)求出抽样中选“支付宝”和“微信”的人数所占百分比,再乘以1800即可.
(1)解:由题意可得:,∵选“网购”的人数为:人,∴选“支付宝”的人数为:人∴,即;
(2)解:由(1)可知选“支付宝”的35人,选“网购”的15人,补全条形统计图如图所示.
(3)解:(名)全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的学生大约有1350名.
【点睛】本题考查条形统计图和扇形统计图,结合两者的信息求总人数,求扇形统计图中某项所占百分比,根据样本所占百分比估计总体.解题的关键是掌握条形统计图和扇形统计图中关联信息,利用关联信息求解.
18.(1)100人,见解析
(2)30,40;
(3)72°
(4)204人
【分析】(1)根据参加书法的人数和所占的百分比,可以计算出参加这次问卷调查的学生人数,然后再根据条形统计图中的数据,即可计算出参加篮球的人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据,可以计算出m、n的值;
(3)用360°乘以书法所占比例即可求出结果;
(4)根据统计图中的数据,可以计算选择摄影所占百分比,再乘以800即可计算出有多少名.
(1)
20÷20%=100(人),
即参加这次问卷调查的学生有100人,
参加“篮球”兴趣小组的有:100×10%=10(人),
补全的条形统计图如图所示;
(2)
m%=×100%=30%,n%=×100%=40%,
即m=30,n=40,
故答案为:30,40;
(3)
扇形统计图中“书法”所对应扇形的圆心角的度数=360°×20%=72°
(4)
800×30%=240(人),
即估计该校选择“摄影”课外兴趣小组的学生有240人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)50;(2)统计图见解析,50.4;(3)132人
【分析】(1)根据C组的人数和所占的百分比,可以求得本次调查的人数;
(2)根据(1)中的结果和条形统计图中的数据,可以算出捐款10元的人数,从而可以将条形统计图补充完整,再根据捐款20元的人数,即可计算出“捐款20元”对应的圆心角的度数;
(3)根据统计图中的数据,可以计算出捐款15元以上(不含15元)的学生估计有多少人.
【详解】解:(1)在本次调查中,一共抽查了14÷28%=50(名),
故答案为:50;
(2)捐款10元的有:50-(9+14+7+4)=16(名),
补全的条形统计图如下图所示,
在扇形统计图中,“捐款20元”对应的圆心角度数是360°× =50.4°,
故答案为:50.4;
(3)600×=132(人),
即捐款15元以上(不含15元)的学生估计有132人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
20.(1)50,20,图见解析
(2)10
(3)200名
【分析】(1)先求出选择折扇课程的学生所占百分比,再利用选择折扇课程的学生人数除以其所占百分比可得参加调查的学生总人数,然后利用参加调查的学生总人数减去选择其他三门课程的学生人数可得参加剪纸课程的学生人数,据此补全条形统计图即可;
(2)利用选择陶艺课程的学生人数除以参加调查的学生总人数即可得;
(3)利用1000乘以选择刺绣课程学生所占的百分比即可得.
【详解】(1)解:选择折扇课程的学生所占百分比为,
参加调查的学生总人数(名),
参加剪纸课程的学生人数为(名),
故答案为:50,20,
补全条形统计图如下:
(2)解:选择“陶艺”课程的学生占比为,
故答案为:10.
(3)解:(名),
答:估计选择“刺绣”课程的学生有200名.
【点睛】本题考查了条形统计图与扇形统计图的信息关联、利用样本估计总体等知识点,熟练掌握统计调查的相关知识是解题关键.
21.见解析
【分析】扇形图中可以知道不达标的百分比是,条形图中不达标人数是人,即可求出六(1)班全体同学的人数,总人数乘以优秀人数的百分比即可求出优秀人数,总人数乘以达标人数的百分比即可求出达标人数.
【详解】解:六(1)班总人数:(人)
优秀等级的人数:(人)
优秀的男生人数:(人)
达标等级的人数:(人)
达标的女生人数:(人)
补全图形如下:
【点睛】本题主要考查统计图形,利用条形图可知各项目的具体数,结合扇形图可知该项目对应的百分比,找出项目的具体数据和对应的百分比的关系是解题的关键.
22.(1)4,1
(2)见解析
(3)48
【分析】(1)根据原始记录可求出n,再根据总数即可求出m;
(2)根据(1)的结果补全图形即可;
(3)先求出样本中步数不少于7500步的人数所占比例,再用团队总人数乘以该比例即可求解.
【详解】(1)根据原始记录可知n=1,
则m=20-(2+10+3+1)=4,
故答案为:4,1;
(2)补全图形如下:
(3)不少于7500步的人数所占比例为:(4+3+1)÷20=40%,
则该团队一天行走不少于7500步的人数为:120×40%=48(人),
即该团队一天行走不少于7500步的人数为48人.
【点睛】本题主要考查了频数分布表和频数分布直方图、用样本估计总体等,解决问题的关键是熟练掌握这些知识点,注重数据处理方法和原始记录表的运用是解答本题的关键.
23.(1)20,0.25;(2)见解析;(3)3300户.
【分析】(1)根据频率=频数÷数据总数计算即可;
(2)根据(1)中的结果画出频数分布直方图即可;
(3)用5000乘以不超过基本月用水量的频率和即可.
【详解】解:(1)10÷0.1=100(人),
m=100×0.2=20(人),
n=25÷100=0.25,
故答案为:20,0.25;
(2)补全频数分布直方图如下:
(3)5000×(0.1+0.2+0.36)=3300(户),
答:该社区5000用户中约有3300户家庭能够全部享受基本价格.
【点睛】本题考查了频数分布表和频数分布直方图的应用,掌握频数、总数、频率之间的关系是解题的关键.也考查了用样本估计总体.
24.(1)96;(2)详见解析;(3)30°;(4)估计该校学生在五一假期阅读时间不少于6h的人数为1200人.
【分析】(1)根据统计图,样本容量:24÷25%;
(2)由(1)可得对应频数:96-8-24-30-10,再画图;
(3)根据圆心角公式:8÷96×360°;
(4)用样本估计总体情况:1800×(人);
【详解】解:(1)样本容量:24÷25%=96;
(2)96-8-24-30-10=24,故统计图如下:
(3)图2中,2≤t<4所在的扇形的圆心角的度数是:8÷96×360°=30°;
(4)1800×(人)
答:计该校学生在五一假期阅读时间不少于6h的人数为1200人
【点睛】考核知识点:频数分布直方图,用样本估计总体;从统计图获取信息是解题的关键.
一、单选题
1.(2022春·湖北咸宁·七年级统考期末)下列调查中,适合用全面调查方式的是( )
A.对全国中学生心理健康现状的调查 B.对某航班旅客上飞机前的安检
C.了解一批签字笔的使用寿命 D.对冷饮市场上冰淇淋质量情况的调查
2.(2022春·湖北武汉·七年级统考期末)要调查下列问题,适合采用全面调查(普查)的是( )
A.中央电视台《开学第一课》的收视率
B.某城市居民6月份人均网上购物的次数
C.即将发射的气象卫星的零部件质量
D.某品牌新能源汽车的最大续航里程
3.(2022春·湖北孝感·七年级统考期末)下列调查中,适宜采用抽样调查的是( )
A.调查一批从疫情中高风险地区来并人员的核酸检测结果
B.调查奥运会马拉松比赛运动员兴奋剂的使用情况
C.调查某批中性笔的使用寿命
D.调查神舟十三号载人飞船各零部件的质量
4.(2022春·湖北恩施·七年级统考期末)为了了解我市6000名学生参加的初中毕业会考数学考试的成绩情况,从中抽取了200名考生的成绩进行统计,在这个问题中,下列说法:(1)这6000名学生的数学会考成绩的全体是总体;(2)每个考生是个体;(3)200名考生是总体的一个样本;(4)样本容量是200,其中说法正确的有( )
A.4个 B.3个 C.2个 D.l个
5.(2022春·湖北襄阳·七年级统考期末)下列调查方式,你认为最合适的是( )
A.为了解全市学生每天参加体育锻炼的时间,采取抽样调查方式
B.襄阳机场对旅客进行登机前安检,采用抽样调查方式
C.为了调查2022年度湖北省人均收入情况,调查省会城市武汉的人均收入
D.要调查一批灯管的使用寿命,采用全面调查的方式
6.(2022春·湖北随州·七年级统考期末)甲、乙、丙三个小组生产帐蓬,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.如图是描述三个小组一天生产帐蓬情况的统计图,从中可以得出人数最多的小组是( )
A.甲组 B.乙组 C.丙组 D.乙、丙两组
7.(2022春·湖北孝感·七年级统考期末)如图所示的两个统计图,女生人数多的学校是( )
A.甲校 B.乙校
C.甲、乙两校女生人数一样多 D.无法确定
8.(2022春·湖北随州·七年级统考期末)2022年北京冬奥会期间,为了记录某一运动员的体温变化情况,应选择的统计图是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
9.(2022春·湖北十堰·七年级统考期末)一个容量为80的样本中,最大数是141,最小数是50,取组距为10,可以分成( )组
A.10组 B.9组 C.8组 D.7组
二、填空题
10.(2022春·湖北襄阳·七年级统考期末)为了考察我市5000名七年级学生数学知识与能力测试的成绩,从中抽取100份试卷进行分析,那么样本容量是_____.
11.(2022春·湖北黄石·七年级统考期末)2020年是抗美援朝胜利70周年,为了解初中生对抗美援朝历史的知晓情况,某校课外兴趣小组在本校2400名学生中展开了调查,随机抽查了200名学生,其中“非常了解”的学生有90名,则可估计该校学生对抗美援朝历史“非常了解”的学生有________名.
12.(2022春·湖北随州·七年级统考期末)在扇形统计图中,有两个扇形的圆心角度数之比为3:4,且较小扇形表示24本课本书,则较大扇形表示___本课本书
13.(2022春·湖北荆门·七年级统考期末)王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码 S M L XL XXL XXL
频率 0.05 0.1 0.2 0.325 0.3 0.025
则该班学生所穿校服尺码为“L”的人数有________个.
14.(2022春·湖北武汉·七年级统考期末)在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是______;
类型 健康 亚健康 不健康
数据(人) 32 7 1
三、解答题
15.(2022春·湖北宜昌·七年级统考期末)学习强国推出了“青年大学习”专题学习,让广大青少年通过丰富多彩的学习形式,形成大格局,富有大智慧.某校为了解学生对此次专题学习的关注程度,抽取了部分学生做问卷调查,用“A”表示“非常了解”,“B”表示“了解”,“C”表示“有所了解”,“D”表示“不了解”,如图甲,乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)设本次问卷调查抽取了n名学生,请直接写出n的值;
(2)将图甲中“B”部分的图形补充完整;
(3)如果该校有学生1000人,请你估计该校学生对此次专题学习关注程度“不了解”的约有多少人?
16.(2022春·湖北咸宁·七年级统考期末)某校组织全体学生开展汉字听写大赛,从中抽取部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,直方图从左至右分别对应A、B、C、D、E组,其中C组图象缺失.已知A组的频数比B组小48.
请你根据图中提供的信息解答下列问题:
(1)求频数分布直方图中a、b的值;
(2)扇形图中D部分扇形所对的圆心角的度数为__________;
(3)若80分以上为优秀,全校共有1000名学生,估计成绩优秀的学生有多少名?
17.(2022春·湖北武汉·七年级统考期末)目前“微信”“支付宝”“共享单车”和“网购”给我们的生活带来了很多便利,九年级数学小组在校内对“你最认可的新生事物”进行调查,随机调查了m名学生(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如图所示不完整的统计图.
(1)根据图中信息,求出__________,__________;
(2)请把条形统计图补充完整;
(3)根据抽样调查的结果,请估算在全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的学生共有多少名.
18.(2022春·湖北襄阳·七年级统考期末)某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图.
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图;
(2)求,的值;
(3)求扇形统计图中“书法”所对应扇形的圆心角的度数.
(4)若该校有800名学生,估计选择摄影的有多少人?
19.(2022春·湖北十堰·七年级统考期末)自从新冠肺炎疫情爆发,我国高度重视并采取了强有力的措施进行防控.武汉是疫情最先爆发的地区,为了帮助武汉人民尽快度过难关,某校八年级全体同学参加了捐款活动.现随机抽查了部分同学捐款的情况统计如图所示;
(1)在本次调查中,一共抽查了__________名学生;
(2)请补全条形统计图,并计算在扇形统计图中,“捐款20元”对应的圆心角度数是_________度;
(3)在八年级600名学生中,捐款15元以上(不含15元)的学生估计有多少人?
20.(2022秋·湖北荆州·七年级校考期末)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 名,参加剪纸的学生有 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 %;
(3)若该校七年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
21.(2022秋·湖北黄石·七年级统考期末)实验小学六(1)班全体同学参加一次体育测试后,分为优秀、达标、不达标三级,并画出下面两张统计图.请把统计图补充完整,并根据图中已知信息写出所要计算的相关数据的计算过程.
22.(2022春·湖北鄂州·七年级统考期末)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
频数分布表
组别 步数分组 频数
A 5500≤x<6500 2
B 6500≤x<7500 10
C 7500≤x<8500 m
D 8500≤x<9500 3
E 9500≤x<10500 n
根据以上信息解答下列问题:
(1)填空:__________,__________
(2)请补全频数分布直方图:
(3)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
23.(2022春·湖北荆门·七年级校考期末)某社区从5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成两幅不完整的统计图表:
平均用水a(吨) 3<a≤6 6<a≤9 9<a≤12 12<a≤15 15<a≤18
频数 10 m 36 25 9
频率 0.1 0.2 0.36 n 0.09
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= .
(2)根据题中数据补全频数分布直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
24.(2022春·湖北咸宁·七年级统考期末)为了解某校学生在五一假期阅读的情况,随机抽取了若干名学生进行调查,获得他们的阅读时间(单位:h),并对数据(时间)进行整理、描述.下面给出了部分信息:图1是阅读时间频数分布直方图(数据分成5组:2≤t<4,4≤t<6,6≤t<8,8≤t<10,10≤t≤12),图2是阅读时间扇形统计图.
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)补全图1;
(3)图2中,2≤t<4所在的扇形的圆心角的度数是 ;
(4)已知该校共有1800名学生,估计该校学生在五一假期阅读时间不少于6h的人数.
参考答案:
1.B
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.对全国中学生心理健康现状的调查,适宜采用抽样调查方式,故本选项不合题意;
B.对某航班旅客上飞机前的安检,适宜采用全面调查,故本选项符合题意;
C.了解一批签字笔的使用寿命,适宜采用抽样调查方式,故本选项不合题意;
D.对冷饮市场上冰淇淋质量情况的调查,适宜采用抽样调查方式,故本选项不合题意;
故选:B.
【点睛】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答即可.
【详解】A、中央电视台《开学第--课》 的收视率适合采用抽样调查方式,故不符合题意;
B、某城市居民6月份人均网上购物的次数适合采用抽样调查方式,故不符合题意;
C、即将发射的气象卫星的零部件质量适合采用全面调查方式,故符合题意;
D、某品牌新能源汽车的最大续航里程适合采用抽样调查方式,故不符合题意,
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.调查一批从疫情中高风险地区来并人员的核酸检测结果,适合全面调查,故本选项不符合题意;
B.调查奥运会马拉松比赛运动员兴奋剂的使用情况,适合全面调查,故本选项不符合题意;
C.调查某批中性笔的使用寿命,适宜采用抽样调查,故本选项符合题意;
D.调查神舟十三号载人飞船各零部件的质量,适合全面调查,故本选项不符合题意.
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.C
【详解】解:本题中的个体是每个考生的数学会考成绩,样本是200名考生的数学会考成绩,
故(2)和(3)错误;
总体是我市6000名学生参加的初中毕业会考数学考试的成绩情况,样本容量是200.
所以(1)和(4)正确.
故选C.
5.A
【分析】根据抽样调查和全面调查的区别进行分析判断.抽样调查是通过对样本调查来估计总体特征,其调查结果是近似的;而全面调查得到的结果比较准确.
【详解】解:A. 为了解全市学生每天参加体育锻炼的时间,采取抽样调查方式,该选项符合题意;
B. 襄阳机场对旅客进行登机前安检,应采用全面调查方式,故该选项不符合题意;
C. 为了调查2022年度湖北省人均收入情况,调查省会城市武汉的人均收入,调查样本不具有代表性和广泛性,故该选项不符合题意;
D. 要调查一批灯管的使用寿命,应采用抽样调查的方式,故该选项不符合题意.
故选:A.
【点睛】本题主要考查了抽样调查和全面调查的知识,解题关键在于理清对调查结果的要求.
6.C
【分析】根据统计图数据,分别求出甲、乙、丙三组的男工人与女工人数,然后比较即可.
【详解】解∶甲组男工人的人数为人,女工人的人数为人,
∴甲组的人数18+6=24人;
乙组男工人的人数为人,女工人的人数为人,
∴乙组的人数16+9=25人;
丙组男工人的人数为人,女工人的人数为人,
∴丙组的人数8+18=26人;
∴丙组的人数最多.
故选:C
【点睛】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
7.D
【详解】试题分析:根据题意,结合扇形图的性质,扇形统计图只能得到每部分所占的比例,具体人数不能直接体现,易得答案.
解:根据题意,因不知道甲乙两校学生的总人数,只知道两校女生占的比例,
故无法比较两校女生的人数,
故选D.
8.A
【分析】根据统计图所表示数据的特点进行判定即可.
【详解】解:为了记录某一运动员的体温变化情况,应该选择折线统计图,
故选择A.
【点睛】本题考查条件图的选择,掌握折线统计图所反映的数据的特点是正确判断的关键,折线统计图反映数据的变化情况,突出变化两个字.
9.A
【分析】根据组数=(最大值-最小值)÷组距来计算即可.
【详解】在样本数据中,最大值为何141,最小值为50,它们的差是141-50=91,由于组距为10,那么由于91÷10=9.1,故可以分成10组.
故选:A.
【点睛】本题考查的是组数的计算,属于基础题,只要根据组数的计算公式来计算即可,注意小数部分结果要进位.
10.100
【分析】直接利用样本容量的定义分析得出答案.
【详解】解:∵从中抽取100份试卷进行分析,
∴样本容量是:100.
故答案为:100.
【点睛】本题考查了总体、个体、样本、样本容量的知识,属于基础题,解答本题的关键是分清具体问题中的总体、个体与样本.
11.1080
【分析】根据题意和题目中的数据,可以通过计算估计出该校学生对抗美援朝历史“非常了解”的学生人数.
【详解】解:估计该校学生对抗美援朝历史“非常了解”的学生人数有人,
故答案为:1080.
【点睛】本题主要考查样本估计总体,掌握总体中所占比值与样本中的所占比值近似相等是解题的关键.
12.32
【分析】分别求出较小的占的比例和较大的占的比例,再求出总书数,最后求出较大扇形表示的书数即可.
【详解】∵较小的占的比例为,较大的占的比例为,
∴总书数(本),
∴56-24=32(本)
∴较大的扇形表示32本书.
【点睛】本题是统计图的基础应用题,难度一般,统计图是中考中的常见知识点,学生需要熟练掌握各个统计图的特点.
13.8
【分析】直接用尺码L的频率乘以班级总人数即可求出答案.
【详解】解:由表可知尺码L的频率的0.2,又因为班级总人数为40,
所以该班学生所穿校服尺码为“L”的人数有400.2=8.
故答案是:8.
【点睛】此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.
14.
【分析】根据频率=频数÷总数,即可得到结论.
【详解】解:由题可知,总人数为32+7+1=40人,测试结果为“健康”的有32人,
测试结果为“健康”的频率=;
故结论是:.
【点睛】本题考查频率,掌握频率、频数、总数之间的关系是解题的关键.
15.(1)200名;(2)见解析;(3)50人
【分析】(1)利用C等级人数÷其对应的百分率求解;
(2)用调查总人数×50%得到B等级的人数,从而补充条形统计图;
(3)利用样本估计总体的思想求解
【详解】解:(1)名
∴本次问卷调查抽取了200名学生
(2)B等级对应的人数为:200×50%=100人
补充统计图如下:
(3)1000×(1-50%-20%-25%)=50人
∴该校学生对此次专题学习关注程度“不了解”的约有50人
【点睛】本题考查的是条形统计图和扇形统计图的应用及用样本估计总体,熟知从条形图可以很容易看出数据的大小,便于比较是解答此题的关键.
16.(1)
(2)
(3)470
【分析】(1)根据扇形统计图中的数据和A组的频数比B组小48,可求得调查人数,后计算出a、b的值即可;
(2)根据直方图中的数据,可计算出扇形图中D部分所对的圆心角度数;
(3)根据扇形统计图中的数据,可以计算出优秀学生有多少人.
【详解】(1)解:本次调查人数为:(人)
,
(2)解:由D所占人数最多,得所占人数为:140
则扇形图中D部分扇形所对的圆心角的度数为:
故答案为:
(3)解:由条形统计图,大于80分的在扇形统计图中占
则1000名学生,估计成绩优秀的学生有:1000(人)
【点睛】本题考查频数分布直方图、用样本估计总体、扇形统计图,明确题意,利用数形结合思想时关键.
17.(1)100,35;
(2)见解析;
(3)1350名.
【分析】(1)利用选“共享单车”人数为10,所占百分比为,即可求出m;利用选“网购”所占百分比为,求出选“网购”的人数,进一步可得选“支付宝”的人数,再除以总人数即可求出其所占百分比;
(2)由(1)求出的数据补充条形图即可;
(3)求出抽样中选“支付宝”和“微信”的人数所占百分比,再乘以1800即可.
(1)解:由题意可得:,∵选“网购”的人数为:人,∴选“支付宝”的人数为:人∴,即;
(2)解:由(1)可知选“支付宝”的35人,选“网购”的15人,补全条形统计图如图所示.
(3)解:(名)全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的学生大约有1350名.
【点睛】本题考查条形统计图和扇形统计图,结合两者的信息求总人数,求扇形统计图中某项所占百分比,根据样本所占百分比估计总体.解题的关键是掌握条形统计图和扇形统计图中关联信息,利用关联信息求解.
18.(1)100人,见解析
(2)30,40;
(3)72°
(4)204人
【分析】(1)根据参加书法的人数和所占的百分比,可以计算出参加这次问卷调查的学生人数,然后再根据条形统计图中的数据,即可计算出参加篮球的人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据,可以计算出m、n的值;
(3)用360°乘以书法所占比例即可求出结果;
(4)根据统计图中的数据,可以计算选择摄影所占百分比,再乘以800即可计算出有多少名.
(1)
20÷20%=100(人),
即参加这次问卷调查的学生有100人,
参加“篮球”兴趣小组的有:100×10%=10(人),
补全的条形统计图如图所示;
(2)
m%=×100%=30%,n%=×100%=40%,
即m=30,n=40,
故答案为:30,40;
(3)
扇形统计图中“书法”所对应扇形的圆心角的度数=360°×20%=72°
(4)
800×30%=240(人),
即估计该校选择“摄影”课外兴趣小组的学生有240人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)50;(2)统计图见解析,50.4;(3)132人
【分析】(1)根据C组的人数和所占的百分比,可以求得本次调查的人数;
(2)根据(1)中的结果和条形统计图中的数据,可以算出捐款10元的人数,从而可以将条形统计图补充完整,再根据捐款20元的人数,即可计算出“捐款20元”对应的圆心角的度数;
(3)根据统计图中的数据,可以计算出捐款15元以上(不含15元)的学生估计有多少人.
【详解】解:(1)在本次调查中,一共抽查了14÷28%=50(名),
故答案为:50;
(2)捐款10元的有:50-(9+14+7+4)=16(名),
补全的条形统计图如下图所示,
在扇形统计图中,“捐款20元”对应的圆心角度数是360°× =50.4°,
故答案为:50.4;
(3)600×=132(人),
即捐款15元以上(不含15元)的学生估计有132人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
20.(1)50,20,图见解析
(2)10
(3)200名
【分析】(1)先求出选择折扇课程的学生所占百分比,再利用选择折扇课程的学生人数除以其所占百分比可得参加调查的学生总人数,然后利用参加调查的学生总人数减去选择其他三门课程的学生人数可得参加剪纸课程的学生人数,据此补全条形统计图即可;
(2)利用选择陶艺课程的学生人数除以参加调查的学生总人数即可得;
(3)利用1000乘以选择刺绣课程学生所占的百分比即可得.
【详解】(1)解:选择折扇课程的学生所占百分比为,
参加调查的学生总人数(名),
参加剪纸课程的学生人数为(名),
故答案为:50,20,
补全条形统计图如下:
(2)解:选择“陶艺”课程的学生占比为,
故答案为:10.
(3)解:(名),
答:估计选择“刺绣”课程的学生有200名.
【点睛】本题考查了条形统计图与扇形统计图的信息关联、利用样本估计总体等知识点,熟练掌握统计调查的相关知识是解题关键.
21.见解析
【分析】扇形图中可以知道不达标的百分比是,条形图中不达标人数是人,即可求出六(1)班全体同学的人数,总人数乘以优秀人数的百分比即可求出优秀人数,总人数乘以达标人数的百分比即可求出达标人数.
【详解】解:六(1)班总人数:(人)
优秀等级的人数:(人)
优秀的男生人数:(人)
达标等级的人数:(人)
达标的女生人数:(人)
补全图形如下:
【点睛】本题主要考查统计图形,利用条形图可知各项目的具体数,结合扇形图可知该项目对应的百分比,找出项目的具体数据和对应的百分比的关系是解题的关键.
22.(1)4,1
(2)见解析
(3)48
【分析】(1)根据原始记录可求出n,再根据总数即可求出m;
(2)根据(1)的结果补全图形即可;
(3)先求出样本中步数不少于7500步的人数所占比例,再用团队总人数乘以该比例即可求解.
【详解】(1)根据原始记录可知n=1,
则m=20-(2+10+3+1)=4,
故答案为:4,1;
(2)补全图形如下:
(3)不少于7500步的人数所占比例为:(4+3+1)÷20=40%,
则该团队一天行走不少于7500步的人数为:120×40%=48(人),
即该团队一天行走不少于7500步的人数为48人.
【点睛】本题主要考查了频数分布表和频数分布直方图、用样本估计总体等,解决问题的关键是熟练掌握这些知识点,注重数据处理方法和原始记录表的运用是解答本题的关键.
23.(1)20,0.25;(2)见解析;(3)3300户.
【分析】(1)根据频率=频数÷数据总数计算即可;
(2)根据(1)中的结果画出频数分布直方图即可;
(3)用5000乘以不超过基本月用水量的频率和即可.
【详解】解:(1)10÷0.1=100(人),
m=100×0.2=20(人),
n=25÷100=0.25,
故答案为:20,0.25;
(2)补全频数分布直方图如下:
(3)5000×(0.1+0.2+0.36)=3300(户),
答:该社区5000用户中约有3300户家庭能够全部享受基本价格.
【点睛】本题考查了频数分布表和频数分布直方图的应用,掌握频数、总数、频率之间的关系是解题的关键.也考查了用样本估计总体.
24.(1)96;(2)详见解析;(3)30°;(4)估计该校学生在五一假期阅读时间不少于6h的人数为1200人.
【分析】(1)根据统计图,样本容量:24÷25%;
(2)由(1)可得对应频数:96-8-24-30-10,再画图;
(3)根据圆心角公式:8÷96×360°;
(4)用样本估计总体情况:1800×(人);
【详解】解:(1)样本容量:24÷25%=96;
(2)96-8-24-30-10=24,故统计图如下:
(3)图2中,2≤t<4所在的扇形的圆心角的度数是:8÷96×360°=30°;
(4)1800×(人)
答:计该校学生在五一假期阅读时间不少于6h的人数为1200人
【点睛】考核知识点:频数分布直方图,用样本估计总体;从统计图获取信息是解题的关键.
