2022--2023学年人教版八年级数学下册18.2.2菱形 课后练习(含答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学下册18.2.2菱形 课后练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 505.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 21:48:30 | ||
图片预览

文档简介
18.2.2菱形
一、单选题
1.如图,菱形的对角线、相交于点,过点作于点,连接,若,,则的长为( )
A. B. C. D.
2.若菱形ABCD的边长为2,其中∠ABC=60°,则菱形ABCD的面积为( )
A.4 B. C.2 D.
3.已知菱形的对角线和的长分别为和,则菱形的面积是( )
A. B. C. D.6
4.能判定一个四边形是菱形的条件是( )
A.对角线互相平分且相等 B.对角线互相垂直且相等
C.对角线互相垂直且对角相等 D.对角线互相垂直,且一条对角线平分一组对角
5.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B坐标是(4,1),点D坐标是(0,1),点A在x轴上,则菱形ABCD的周长是( )
A.8 B.2 C.4 D.12
6.依次连接等腰梯形各边的中点得到的四边形是( )
A.菱形 B.矩形 C.正方形 D.等腰梯形
7.菱形的周长为,它的一条对角线的长为,则菱形的另一条对角线的长为( )
A. B. C. D.
8.下列命题错误的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线相等
C.对角线互相垂直平分的四边形是菱形 D.对角线相等的四边形是矩形
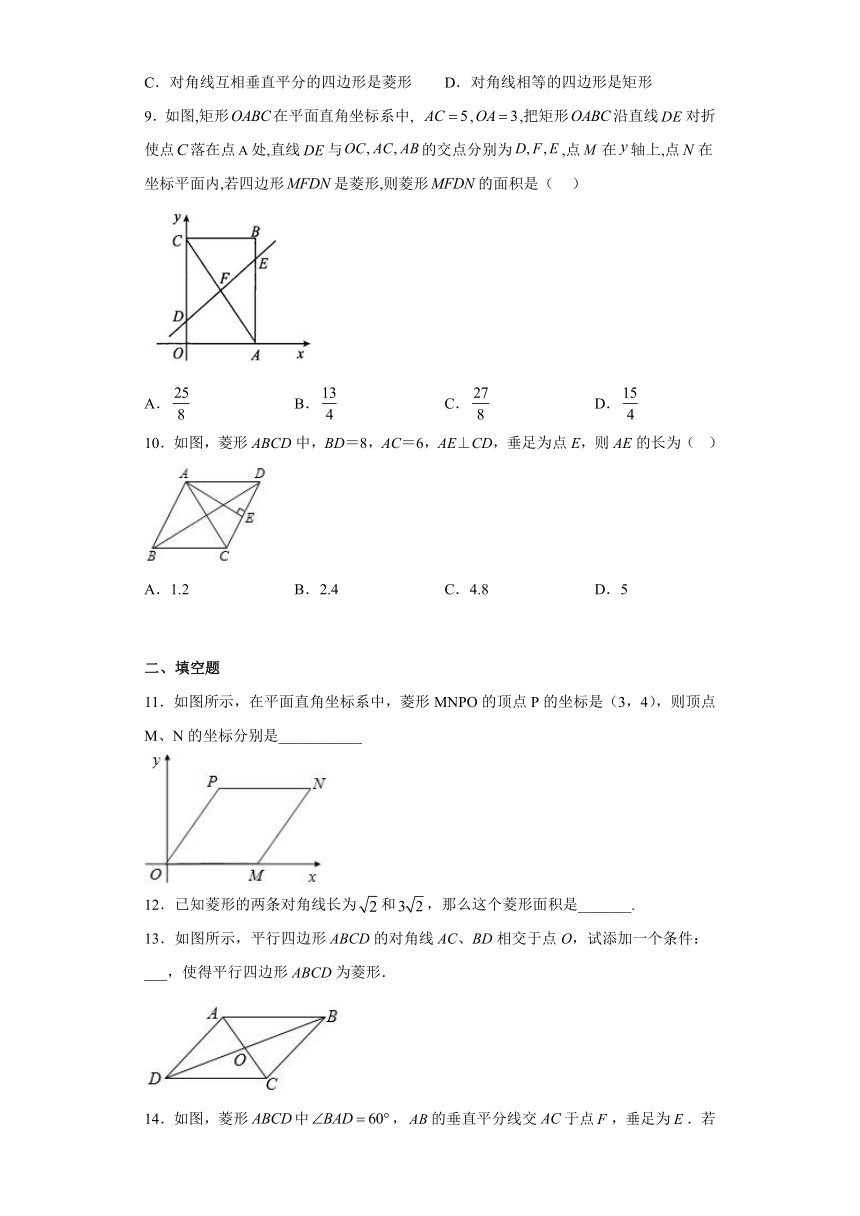
9.如图,矩形在平面直角坐标系中, ,,把矩形沿直线对折使点落在点处,直线与的交点分别为,点在轴上,点在坐标平面内,若四边形是菱形,则菱形的面积是( )
A. B. C. D.
10.如图,菱形ABCD中,BD=8,AC=6,AE⊥CD,垂足为点E,则AE的长为( )
A.1.2 B.2.4 C.4.8 D.5
二、填空题
11.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是___________
12.已知菱形的两条对角线长为和,那么这个菱形面积是_______.
13.如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件:___,使得平行四边形ABCD为菱形.
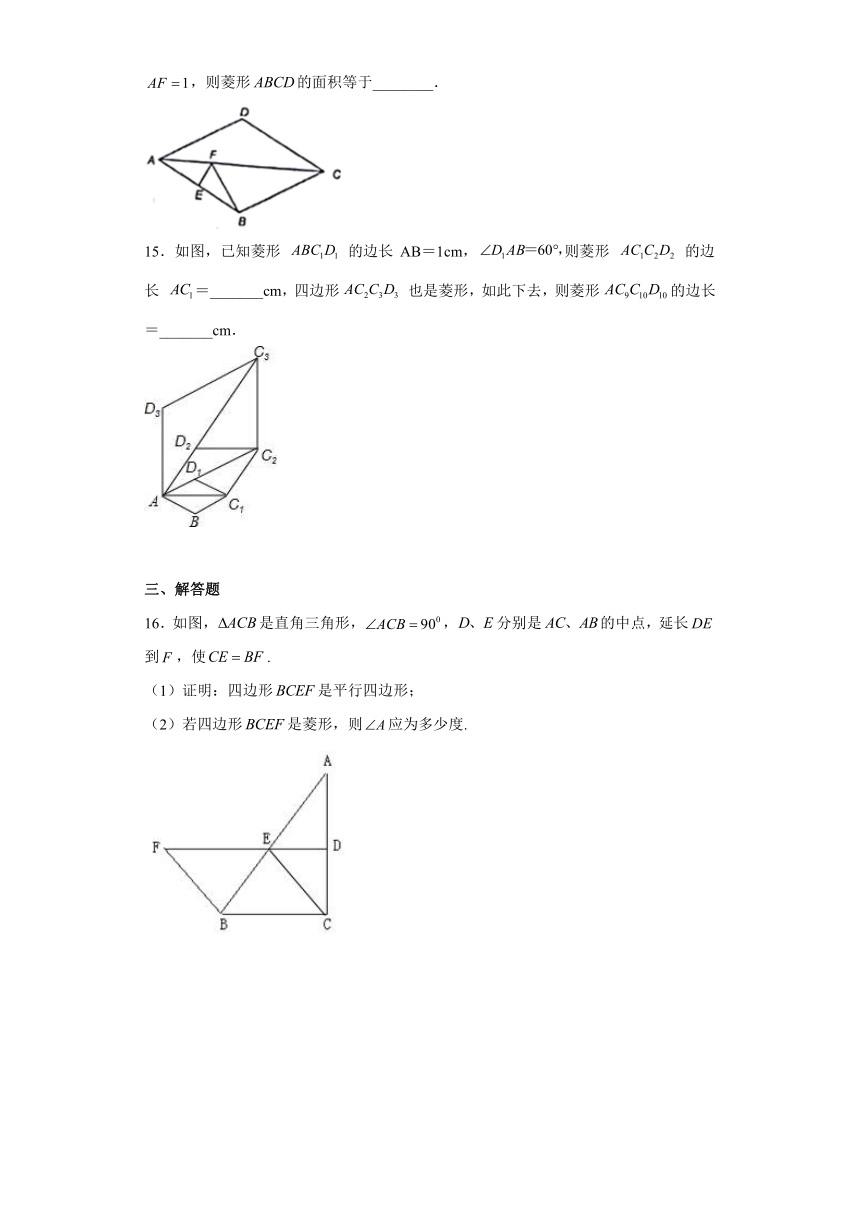
14.如图,菱形中,的垂直平分线交于点,垂足为.若,则菱形的面积等于________.
15.如图,已知菱形 的边长 AB=1cm,则菱形 的边长 =_______cm,四边形 也是菱形,如此下去,则菱形的边长=_______cm.
三、解答题
16.如图,是直角三角形,,分别是的中点,延长到,使.
(1)证明:四边形是平行四边形;
(2)若四边形是菱形,则应为多少度.
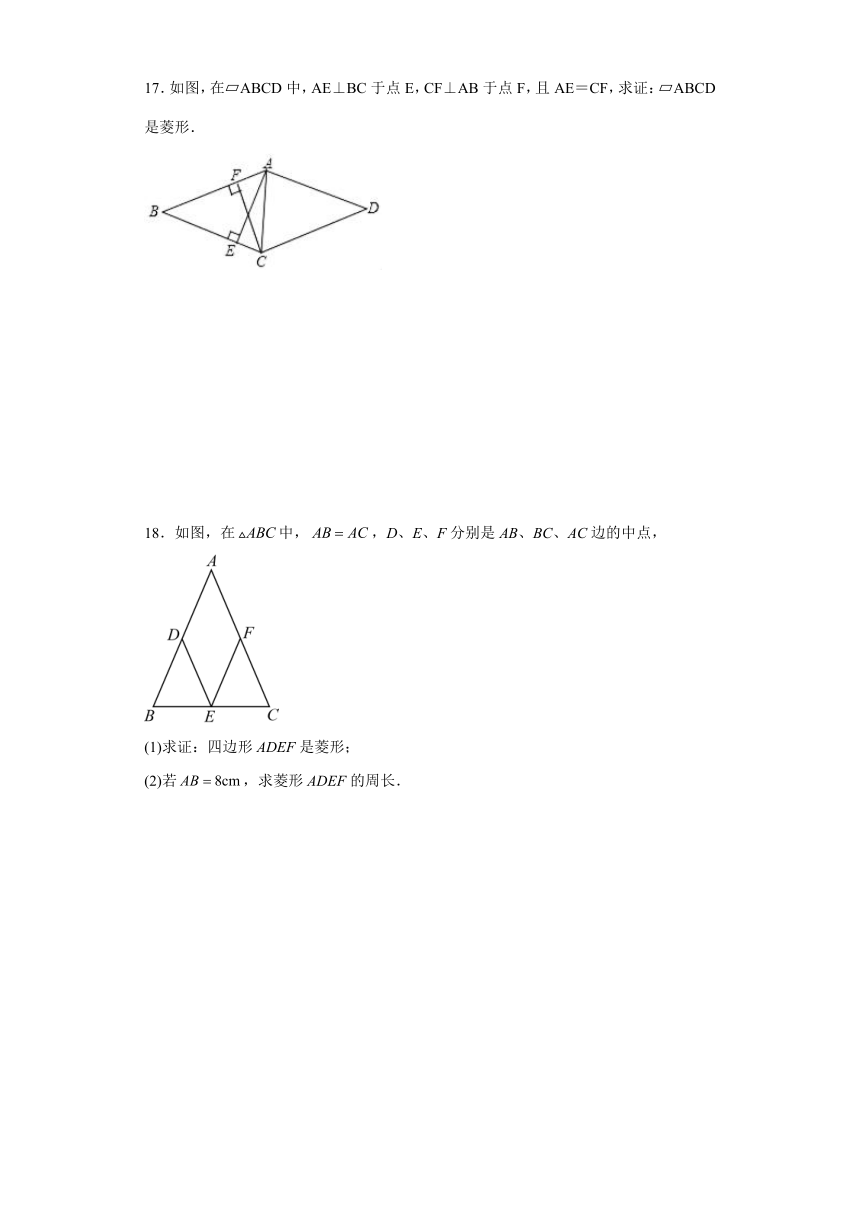
17.如图,在 ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,求证: ABCD是菱形.
18.如图,在中,,D、E、F分别是AB、BC、AC边的中点,
(1)求证:四边形ADEF是菱形;
(2)若,求菱形ADEF的周长.
19.如图,在正方形方格纸中,线段的两个端点和点都在小方格的格点上,分别按下列要求画格点四边形.
(1)在图甲中画一个以为边的平行四边形(不能画矩形),使点落在的对边上(不包括端点).
(2)在图乙中画一个以为对角线的菱形(不能画正方形),使点落在菱形的内部(不包括边界).
20.已知点是平行四边形边上的一点(不与点,重合).
(1)如图1,当点运动到的中点时,连接、,若平分,证明:;
(2)如图2,过点作交直线于点,连接.若,,,在线段上是否存在一点,使得四边形为菱形?若存在,请求出,的长;若不存在,请简单地说明理由.
参考答案
1.A
2.D
3.B
4.C
5.C
6.A
7.A
8.D
9.C
10.C
11.M(5,0),N(8,4)
12.3
13.AD=DC(答案不唯一)
14.
15. 81
16.(1)证明:∵是直角三角形
且是中点,
∴,∴
∵,∴,
∴;
∵是中点,
∴,∴
∴,
∴,
∴四边形是平行四边形;
(2)解:∵是菱形,∴,
∵是直角三角形,
∴.
故答案为(1)见解析;(2).
17.证明:∵AE⊥BC于点E,CF⊥AB于点F,
∴∠CFB=∠AEB=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴BC=BA
∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
18. (1)
∵D、E、F分别是AB、BC、AC边的中点,
∴DE、EF是△ABC的中位线,
∴,,
∵,
∴
∴四边形ADEF是菱形;
(2)
由(1)得
∴菱形ADEF的周长为cm.
19.解:(1)如甲图所示,
(2)如乙图所示,
20. (1)证明:四边形是平行四边形,,,.又平分,,,.又是的中点,,;
(2)解:存在,当且时,四边形为菱形.理由如下:过点作于,如图所示:四边形是平行四边形,,,,,在中,,,,,,,在中,,,,,,.又在中,,点在的延长线上,,四边形是平行四边形.又,是菱形
一、单选题
1.如图,菱形的对角线、相交于点,过点作于点,连接,若,,则的长为( )
A. B. C. D.
2.若菱形ABCD的边长为2,其中∠ABC=60°,则菱形ABCD的面积为( )
A.4 B. C.2 D.
3.已知菱形的对角线和的长分别为和,则菱形的面积是( )
A. B. C. D.6
4.能判定一个四边形是菱形的条件是( )
A.对角线互相平分且相等 B.对角线互相垂直且相等
C.对角线互相垂直且对角相等 D.对角线互相垂直,且一条对角线平分一组对角
5.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B坐标是(4,1),点D坐标是(0,1),点A在x轴上,则菱形ABCD的周长是( )
A.8 B.2 C.4 D.12
6.依次连接等腰梯形各边的中点得到的四边形是( )
A.菱形 B.矩形 C.正方形 D.等腰梯形
7.菱形的周长为,它的一条对角线的长为,则菱形的另一条对角线的长为( )
A. B. C. D.
8.下列命题错误的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线相等
C.对角线互相垂直平分的四边形是菱形 D.对角线相等的四边形是矩形
9.如图,矩形在平面直角坐标系中, ,,把矩形沿直线对折使点落在点处,直线与的交点分别为,点在轴上,点在坐标平面内,若四边形是菱形,则菱形的面积是( )
A. B. C. D.
10.如图,菱形ABCD中,BD=8,AC=6,AE⊥CD,垂足为点E,则AE的长为( )
A.1.2 B.2.4 C.4.8 D.5
二、填空题
11.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是___________
12.已知菱形的两条对角线长为和,那么这个菱形面积是_______.
13.如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件:___,使得平行四边形ABCD为菱形.
14.如图,菱形中,的垂直平分线交于点,垂足为.若,则菱形的面积等于________.
15.如图,已知菱形 的边长 AB=1cm,则菱形 的边长 =_______cm,四边形 也是菱形,如此下去,则菱形的边长=_______cm.
三、解答题
16.如图,是直角三角形,,分别是的中点,延长到,使.
(1)证明:四边形是平行四边形;
(2)若四边形是菱形,则应为多少度.
17.如图,在 ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,求证: ABCD是菱形.
18.如图,在中,,D、E、F分别是AB、BC、AC边的中点,
(1)求证:四边形ADEF是菱形;
(2)若,求菱形ADEF的周长.
19.如图,在正方形方格纸中,线段的两个端点和点都在小方格的格点上,分别按下列要求画格点四边形.
(1)在图甲中画一个以为边的平行四边形(不能画矩形),使点落在的对边上(不包括端点).
(2)在图乙中画一个以为对角线的菱形(不能画正方形),使点落在菱形的内部(不包括边界).
20.已知点是平行四边形边上的一点(不与点,重合).
(1)如图1,当点运动到的中点时,连接、,若平分,证明:;
(2)如图2,过点作交直线于点,连接.若,,,在线段上是否存在一点,使得四边形为菱形?若存在,请求出,的长;若不存在,请简单地说明理由.
参考答案
1.A
2.D
3.B
4.C
5.C
6.A
7.A
8.D
9.C
10.C
11.M(5,0),N(8,4)
12.3
13.AD=DC(答案不唯一)
14.
15. 81
16.(1)证明:∵是直角三角形
且是中点,
∴,∴
∵,∴,
∴;
∵是中点,
∴,∴
∴,
∴,
∴四边形是平行四边形;
(2)解:∵是菱形,∴,
∵是直角三角形,
∴.
故答案为(1)见解析;(2).
17.证明:∵AE⊥BC于点E,CF⊥AB于点F,
∴∠CFB=∠AEB=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴BC=BA
∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
18. (1)
∵D、E、F分别是AB、BC、AC边的中点,
∴DE、EF是△ABC的中位线,
∴,,
∵,
∴
∴四边形ADEF是菱形;
(2)
由(1)得
∴菱形ADEF的周长为cm.
19.解:(1)如甲图所示,
(2)如乙图所示,
20. (1)证明:四边形是平行四边形,,,.又平分,,,.又是的中点,,;
(2)解:存在,当且时,四边形为菱形.理由如下:过点作于,如图所示:四边形是平行四边形,,,,,在中,,,,,,,在中,,,,,,.又在中,,点在的延长线上,,四边形是平行四边形.又,是菱形
