9.1.3 三角形的三边关系 课件(共29张PPT)
文档属性
| 名称 | 9.1.3 三角形的三边关系 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 11:39:57 | ||
图片预览




文档简介
(共29张PPT)
9.1.3 三角形的三边关系
华师大版 七年级 下册
教学目标
教学目标:1.掌握三角形三边关系,理解三角形具有稳定性.
2.会用三角形的三边关系进行相关计算或比较.
教学重点:三角形任何两边之和大于第三边的应用.
教学难点:已知三角形的两边求第三边的范围.
新知导入
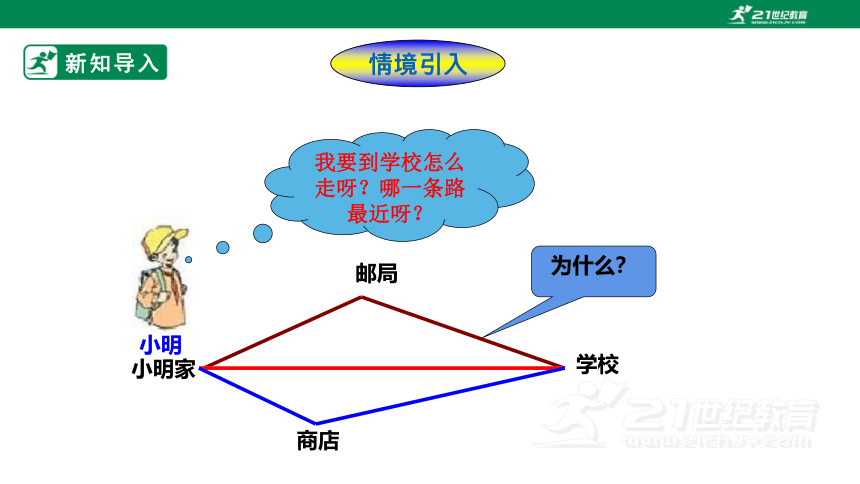
情境引入
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
新知讲解
合作学习
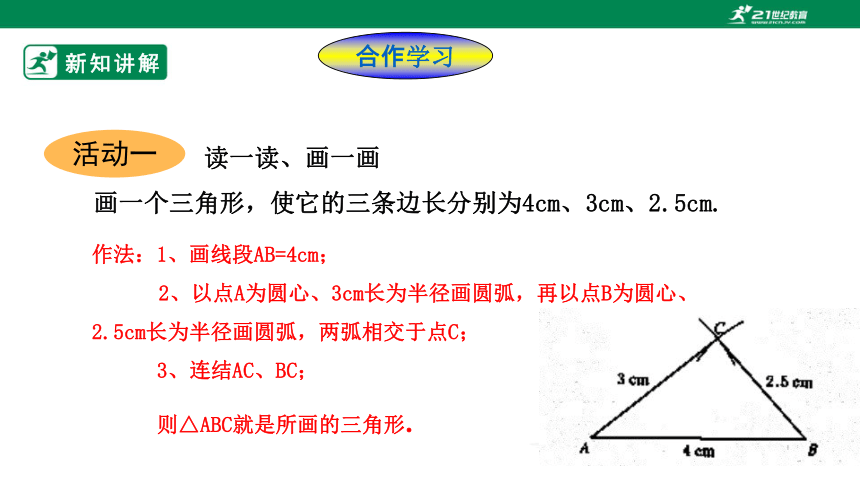
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5cm长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
活动一
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
任意选择三条线段画三角形,你能画出哪些类型的三角形?
活动二
2
2
4
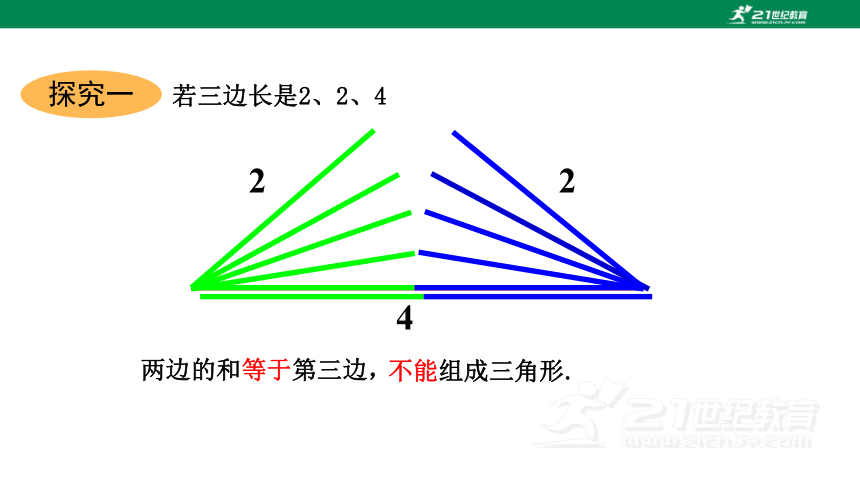
若三边长是2、2、4
两边的和等于第三边,
不能组成三角形.
探究一
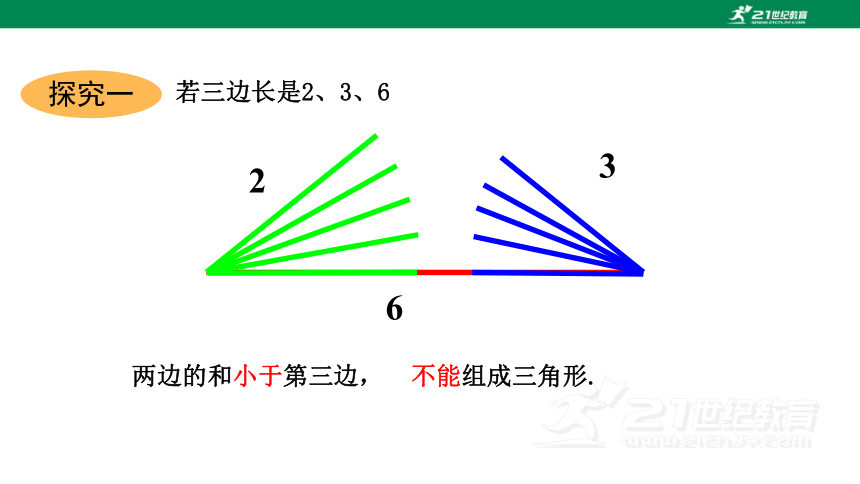
两边的和小于第三边,
不能组成三角形.
2
3
6
若三边长是2、3、6
探究一
4
5
6
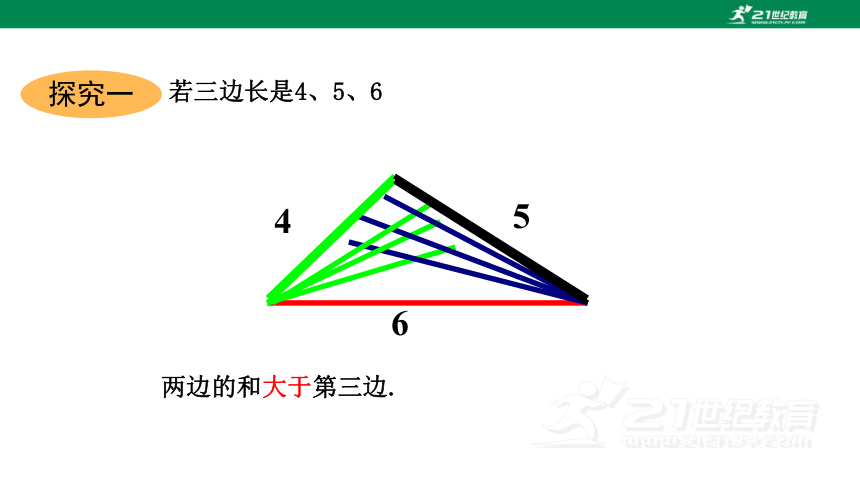
两边的和大于第三边.
若三边长是4、5、6
探究一
因此,并不是任意三条线段都可以组成一个三角形.
在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
归纳
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
想一想
由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
两点之间,线段最短.
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
a
b
A
B
C
c
提炼概念
小结:
三角形的任何两边的和大于第三边
三角形的任何两边的差小于第三边
问题:
如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
答: 三角形形状不会改变,四边形形状会改变,这就是说,三角形具有稳定性,四边形没有稳定性。
用三根木条钉一个三角形,你会发现再也无法改变这个三角形的形状和大小,也就是说,如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性.
用四根木条钉一个四边形,你会发现这个四边形的形状和大小都可以改变,这说明四边形不具有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
三角形的稳定性在生产实践中有着广泛的应用.例如桥梁拉杆
(如图9.1.15所示)、电视塔架底座,都是三角形结构.
图9.1.15
典例精讲
解:(1)能.因为3 + 4>5,
符合三角形两边的和大于第三边.
(2)不能.因为5 + 6 =11,
不符合三角形两边的和大于第三边.
(3)能.因为5 + 6>10,
符合三角形两边的和大于第三边.
例:下列长度的三条线段能否组成三角形?为什么?
(1)3,4,5;(2)5,6,11;(3)5,6,10.
归纳概念
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
思考:解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
课堂练习
1.一个三角形的两边长为3和8,第三边长为奇数,则第三边长为( )
A. 5或7 B. 7或9 C. 7 D. 9
B
2.设三角形三边的长分别为3,7,1+a,则a的取值范围为________.
3<a<9
3.以下列长度的三条线段为边,能构成三角形的有哪些?
(1)6 cm,8 cm,10 cm;
(2)5 cm,8 cm,2 cm;
(3)三条线段之比为4∶5∶6;
(4)a+1,a+2,a+3(a>0).
解:(1)(3)(4)能构成三角形,(2)不能构成三角形
4.已知等腰三角形两条边长分别为4cm、8cm,求等腰三角形的周长.
解:①若腰长是4cm, 则4+4=8cm(不符合三角形的三边关系,两边之和大于第三边)
所以,不可以构成三角形
②若腰长是8cm,则4+8=12cm>8cm
周长是:4+8+8=20cm
∴等腰三角形的周长是20cm
5.一个三角形的两边长为3和5.
(1)求它的第三边长a的取值范围;
(2)求它的周长C的取值范围;
(3)若周长为偶数,求三角形的第三边长.
解:(1)根据三角形的三边关系可得5-3<a<5+3,
即2<a<8.
(2) ∵第三边长a的取值范围为2<a<8,
∴周长C的取值范围为2+3+5<C<5+3+8,
即10<C<16.
(3)解:∵周长C的取值范围为10<C<16且周长为偶数,
∴周长可取12,14,
∵三角形两边长为3和5,
∴第三边长为4或6.
6.有长20 cm,90 cm,100 cm的三根木条,不小心将100 cm的一根折断了,怎么也钉不成三角形木架,问:
(1)最长的木条至少折去了多少厘米?
(2)如果最长的木条折去了45 cm,你怎样通过截木条的方法钉成一个小三角形木架?
解:(1)第三边长x的取值范围为70<x<110,最长木条至少折去了30 cm
(2)三根木条长为20 cm,90 cm,55 cm,因为20+55<90,设把90 cm长的木条截去k cm变为y cm,35<y<75,35<90-k<75,所以15<k<55,即把90 cm长的木条截去的长度在15 cm至55 cm之间,就能钉成一个小三角形木架.
课堂总结
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
应用
稳定性
三角形
独有性质
应用
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
9.1.3 三角形的三边关系
华师大版 七年级 下册
教学目标
教学目标:1.掌握三角形三边关系,理解三角形具有稳定性.
2.会用三角形的三边关系进行相关计算或比较.
教学重点:三角形任何两边之和大于第三边的应用.
教学难点:已知三角形的两边求第三边的范围.
新知导入
情境引入
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
新知讲解
合作学习
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5cm长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
活动一
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
任意选择三条线段画三角形,你能画出哪些类型的三角形?
活动二
2
2
4
若三边长是2、2、4
两边的和等于第三边,
不能组成三角形.
探究一
两边的和小于第三边,
不能组成三角形.
2
3
6
若三边长是2、3、6
探究一
4
5
6
两边的和大于第三边.
若三边长是4、5、6
探究一
因此,并不是任意三条线段都可以组成一个三角形.
在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
归纳
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
想一想
由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
两点之间,线段最短.
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
a
b
A
B
C
c
提炼概念
小结:
三角形的任何两边的和大于第三边
三角形的任何两边的差小于第三边
问题:
如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
答: 三角形形状不会改变,四边形形状会改变,这就是说,三角形具有稳定性,四边形没有稳定性。
用三根木条钉一个三角形,你会发现再也无法改变这个三角形的形状和大小,也就是说,如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性.
用四根木条钉一个四边形,你会发现这个四边形的形状和大小都可以改变,这说明四边形不具有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
三角形的稳定性在生产实践中有着广泛的应用.例如桥梁拉杆
(如图9.1.15所示)、电视塔架底座,都是三角形结构.
图9.1.15
典例精讲
解:(1)能.因为3 + 4>5,
符合三角形两边的和大于第三边.
(2)不能.因为5 + 6 =11,
不符合三角形两边的和大于第三边.
(3)能.因为5 + 6>10,
符合三角形两边的和大于第三边.
例:下列长度的三条线段能否组成三角形?为什么?
(1)3,4,5;(2)5,6,11;(3)5,6,10.
归纳概念
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
思考:解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
课堂练习
1.一个三角形的两边长为3和8,第三边长为奇数,则第三边长为( )
A. 5或7 B. 7或9 C. 7 D. 9
B
2.设三角形三边的长分别为3,7,1+a,则a的取值范围为________.
3<a<9
3.以下列长度的三条线段为边,能构成三角形的有哪些?
(1)6 cm,8 cm,10 cm;
(2)5 cm,8 cm,2 cm;
(3)三条线段之比为4∶5∶6;
(4)a+1,a+2,a+3(a>0).
解:(1)(3)(4)能构成三角形,(2)不能构成三角形
4.已知等腰三角形两条边长分别为4cm、8cm,求等腰三角形的周长.
解:①若腰长是4cm, 则4+4=8cm(不符合三角形的三边关系,两边之和大于第三边)
所以,不可以构成三角形
②若腰长是8cm,则4+8=12cm>8cm
周长是:4+8+8=20cm
∴等腰三角形的周长是20cm
5.一个三角形的两边长为3和5.
(1)求它的第三边长a的取值范围;
(2)求它的周长C的取值范围;
(3)若周长为偶数,求三角形的第三边长.
解:(1)根据三角形的三边关系可得5-3<a<5+3,
即2<a<8.
(2) ∵第三边长a的取值范围为2<a<8,
∴周长C的取值范围为2+3+5<C<5+3+8,
即10<C<16.
(3)解:∵周长C的取值范围为10<C<16且周长为偶数,
∴周长可取12,14,
∵三角形两边长为3和5,
∴第三边长为4或6.
6.有长20 cm,90 cm,100 cm的三根木条,不小心将100 cm的一根折断了,怎么也钉不成三角形木架,问:
(1)最长的木条至少折去了多少厘米?
(2)如果最长的木条折去了45 cm,你怎样通过截木条的方法钉成一个小三角形木架?
解:(1)第三边长x的取值范围为70<x<110,最长木条至少折去了30 cm
(2)三根木条长为20 cm,90 cm,55 cm,因为20+55<90,设把90 cm长的木条截去k cm变为y cm,35<y<75,35<90-k<75,所以15<k<55,即把90 cm长的木条截去的长度在15 cm至55 cm之间,就能钉成一个小三角形木架.
课堂总结
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
应用
稳定性
三角形
独有性质
应用
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
