新人教版八年级数学下册18.1勾股定理(第一课时)教案
文档属性
| 名称 | 新人教版八年级数学下册18.1勾股定理(第一课时)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 660.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 06:30:28 | ||
图片预览

文档简介
18.1勾股定理(第一课时)
1,教学目标
(1)知识与技能
探索直角三角形三边的关系,了解勾股定理的发现过程。掌握勾股定理的内容,并运用勾股定理进行简单的计算。
(2)数学思考
在探索勾股定理的过程中,让学生经历“观察,猜想,归纳”的能力,并体会数形结合和由特殊到一般的思想方法。
(3)问题解决
通过画图,计算面积,探究勾股定理的内容。
(4)情感态度
通过探索直角三角形三边之间的关系,培养学生积极参与,合作交流的意识,体验获得成功的喜悦。通过介绍勾股定理在中国古代的研究情况,提高学生的民族自豪感。
2,教学重难点
重点:了解勾股定理的演绎过程,掌握勾股定理及其简单的计算。
难点:理解勾股定理的演绎和推导过程。
3,教学方法
探讨法,发现法
四,教学过程
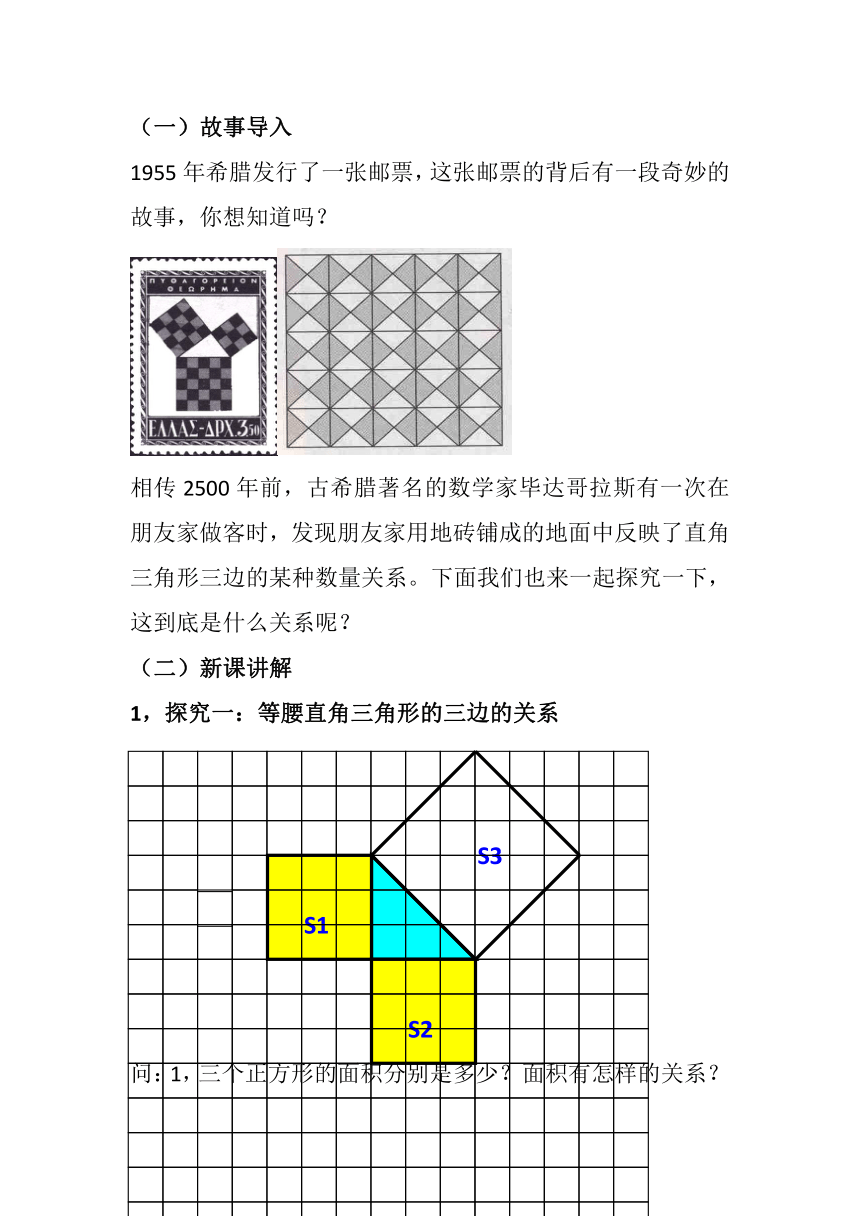
(1)故事导入
1955年希腊发行了一张邮票,这张邮票的背后有一段奇妙的故事,你想知道吗?
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系。下面我们也来一起探究一下,这到底是什么关系呢?
(2)新课讲解
1,探究一:等腰直角三角形的三边的关系
问:1,三个正方形的面积分别是多少?面积有怎样的关系?
2,直角三角形的三边有怎样的关系?
2,探究二:一般直角三角形的三边关系
学生同桌合作在网格纸上画一个一般直角三角形,并向三角形三边外分别以三边长度做正方形。计算三个正方形的面积,找一找三个三角形面积之间的关系并推出一般直角三角形三边的关系。
3,教师几何画板演示:无论如何改变直角三角形的三边的大小,都始终存在着这种关系。
4,勾股定理(毕达哥拉斯定理)
文字语言:直角三角形的两直角边的平方和等于斜边的平方。
符号语言:如果直角三角形两直角边分别为a,b, 斜边为c,那么
(3)巩固练习
思考:使用勾股定理有哪些需要注意的呢?
1,适用范围(条件):直角三角形。
2,分清谁是直角边,谁是斜边,必要时需要分类讨论。
五,课堂小结
通过本节课的学习,你有哪些收获?
6,布置作业
秒变勾股图:
S1
S2
S3
a
c
b
2、在Rt△ABC中,如果两条直角边的长分别为3和4,求第三边的长?
变式:Rt△ABC中,已知两条边长分别为3和4,求第三边的长?
使用勾股定理有哪些要注意的呢?
如果我们分别以Rt△ABC的三边为边(或直径),向外画三个正三角形
(或半圆),那么这三个正三角形(或半圆)的面积之间又有什么样的
关系?
1,教学目标
(1)知识与技能
探索直角三角形三边的关系,了解勾股定理的发现过程。掌握勾股定理的内容,并运用勾股定理进行简单的计算。
(2)数学思考
在探索勾股定理的过程中,让学生经历“观察,猜想,归纳”的能力,并体会数形结合和由特殊到一般的思想方法。
(3)问题解决
通过画图,计算面积,探究勾股定理的内容。
(4)情感态度
通过探索直角三角形三边之间的关系,培养学生积极参与,合作交流的意识,体验获得成功的喜悦。通过介绍勾股定理在中国古代的研究情况,提高学生的民族自豪感。
2,教学重难点
重点:了解勾股定理的演绎过程,掌握勾股定理及其简单的计算。
难点:理解勾股定理的演绎和推导过程。
3,教学方法
探讨法,发现法
四,教学过程
(1)故事导入
1955年希腊发行了一张邮票,这张邮票的背后有一段奇妙的故事,你想知道吗?
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系。下面我们也来一起探究一下,这到底是什么关系呢?
(2)新课讲解
1,探究一:等腰直角三角形的三边的关系
问:1,三个正方形的面积分别是多少?面积有怎样的关系?
2,直角三角形的三边有怎样的关系?
2,探究二:一般直角三角形的三边关系
学生同桌合作在网格纸上画一个一般直角三角形,并向三角形三边外分别以三边长度做正方形。计算三个正方形的面积,找一找三个三角形面积之间的关系并推出一般直角三角形三边的关系。
3,教师几何画板演示:无论如何改变直角三角形的三边的大小,都始终存在着这种关系。
4,勾股定理(毕达哥拉斯定理)
文字语言:直角三角形的两直角边的平方和等于斜边的平方。
符号语言:如果直角三角形两直角边分别为a,b, 斜边为c,那么
(3)巩固练习
思考:使用勾股定理有哪些需要注意的呢?
1,适用范围(条件):直角三角形。
2,分清谁是直角边,谁是斜边,必要时需要分类讨论。
五,课堂小结
通过本节课的学习,你有哪些收获?
6,布置作业
秒变勾股图:
S1
S2
S3
a
c
b
2、在Rt△ABC中,如果两条直角边的长分别为3和4,求第三边的长?
变式:Rt△ABC中,已知两条边长分别为3和4,求第三边的长?
使用勾股定理有哪些要注意的呢?
如果我们分别以Rt△ABC的三边为边(或直径),向外画三个正三角形
(或半圆),那么这三个正三角形(或半圆)的面积之间又有什么样的
关系?
