北师大版六下第4单元正比例和反比例能力拓展卷(含答案)
文档属性
| 名称 | 北师大版六下第4单元正比例和反比例能力拓展卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 15:57:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4单元正比例和反比例能力拓展卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.下列各式(a、b均不为0),a和b成反比例的是( )。
A. B. C.
2.下面各题,两种量成正比例关系的是( )。
A.汽车的速度一定,行驶的时间和路程
B.平行四边形面积一定,它的底和高
C.圆的面积与它的半径
3.淘气从家里到学校(路程不变),他行走的时间和行走的速度( )。
A.成正比例 B.成反比例 C.不成比例
4.仔细观察下表,表中相对应的两个量( )。
单价(元) 1 2 3 4 5 6
件数(件) 600 300 200 150 120 100
A.成正比例 B.成反比例 C.不成比例
5.当梯形的( )一定时,梯形的面积与高成正比例。
A.上底 B.下底 C.上、下底之和
6.比例尺一定,图上距离与实际距离成( )。
A.正比例 B.反比例 C.不成比例
二、填空题
7.如果(a,b均不为0),那么a∶b=( )。如果x∶1.5=y(x,y均不为0),那么x∶y=( ),x和y成( )比例。
8.如果知道圆柱的体积,那么圆柱的底面积和高成( )比例。
9.一个水龙头不断地流水,右图表示的是流出水的体积和时间的关系。
(1)从图中可知,流出水的体积和时间成( )关系。
(2)照这样计算,50分流水( )L,要流出180L水,需要( )分。
10.把一根木料锯成4段要用12分钟,照这样,如果锯成8段,一共需要( )分钟。
11.已知(x、y均不为0),则x、y成( )比例,( )。
12.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
13.《童话书》的单价一定,购买的本数与总价成( )比例。
14.同时同地直立在地面上的物体在阳光下的影长与物体高度成正比例。笑笑身高1.5米,她量了旁边大楼影长为30米,此时笑笑的影子长度刚好1米。据此计算出这座大楼高度约是( )米。
三、判断题
15.如果,则与成反比例。( )
16.和是两种相关联的量,如果,那么和成反比例。( )
17.正方形的边长和面积成正比例。( )
18.圆的半径和面积既不成正比例关系也不成反比例关系。( )
19.长方形的周长一定,它的长和宽成反比例关系。( )
四、计算题
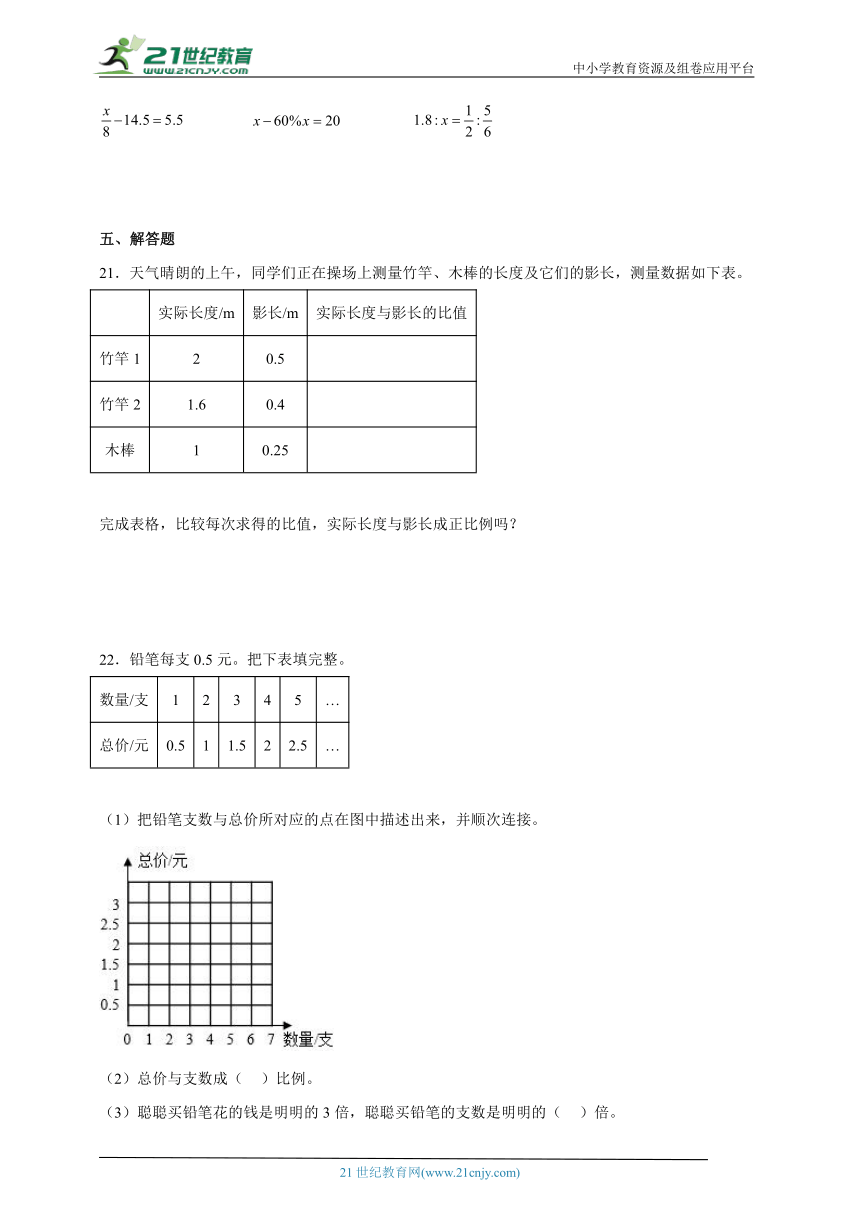
20.解方程。
五、解答题
21.天气晴朗的上午,同学们正在操场上测量竹竿、木棒的长度及它们的影长,测量数据如下表。
实际长度/m 影长/m 实际长度与影长的比值
竹竿1 2 0.5
竹竿2 1.6 0.4
木棒 1 0.25
完成表格,比较每次求得的比值,实际长度与影长成正比例吗?
22.铅笔每支0.5元。把下表填完整。
数量/支 1 2 3 4 5 …
总价/元 0.5 1 1.5 2 2.5 …
(1)把铅笔支数与总价所对应的点在图中描述出来,并顺次连接。
(2)总价与支数成( )比例。
(3)聪聪买铅笔花的钱是明明的3倍,聪聪买铅笔的支数是明明的( )倍。
23.果园里种植一批桃树,桃树的行数和每行棵数如下表:
桃树的行数 4 6 10 15 20 …
每行棵数 30 20 12 8 6 …
(1)写出几组相对应的桃树的行数和每行棵数的积。看一看,积相等吗?
(2)这个积表示的实际意义是什么?
(3)桃树的行数和每行的棵数成反比例吗?为什么?
24.小聪家装修客厅,如果用每块面积是0.36平方米的地砖铺地,铺满要用112块;如果改用每块面积是0.16平方米的地砖铺地,铺满客厅要用多少块?
25.下面是小华6~10岁的身高情况统计表。
年龄/岁 6 7 8 9 10
身高/厘米 112 118 125 130 136
(1)上表中有哪两种变化的量?
(2)这两种量是怎样变化的?
参考答案:
1.B
【分析】如果a和b成反比例,则a和b的积一定。据此把各选项的式子进行转化。
【详解】A.,则,a÷b=÷8=(一定),a和b的商一定,则a和b成正比例;
B.,则,ab=3(一定),a和b的积一定,则a和b成反比例;
C.,则2a-b=5,a和b的商和积都不一定,则a和b不成比例。
故答案为:B
【点睛】本题考查反比例的辨认,把原式转化为a和b相乘或相除的形式是解题的关键。
2.A
【分析】两种相关联的量,如果它们对应的比值一定,那么这两个量就成正比例关系。据此选择。
【详解】A.路程÷时间=速度(一定),比值一定,所以汽车的速度一定,行驶的时间和路程成正比例关系。
B.底×高=面积(一定),乘积一定,所以平行四边形面积一定,它的底和高成反比例关系。
C.圆的面积与它的半径不成比例。
故答案为:A
【点睛】此题考查了正比例的辨别,主要看两个量是否是对应的比值一定。
3.B
【分析】两个相关联的量,如果它们对应的比值一定则成正比例关系,如果它们对应的乘积一定,则成反比例关系,据此解答。
【详解】行走的时间×行走的速度=路程(不变),乘积一定,所以成反比例关系。
故答案为:B
【点睛】此题考查了正反比例的辨别,关键看两个量是比值一定还是乘积一定。
4.B
【分析】单价×件数=总价,观察表格发现各种单价下与对应的件数相乘的乘积都是600,据此结合正比例反比例的定义,选出正确选项即可。
【详解】观察表格发现,单价与对应件数的乘积是一定的,所以单价和件数成反比例。
故答案为:B
【点睛】本题考查了正比例和反比例,乘积一定的两个量成反比例,商一定的两个量成正比例。
5.C
【分析】根据梯形的面积公式:梯形面积=(上底+下底)×高÷2,上底+下底的和一定,梯形面积与高成正比例。
【详解】由分析可知,梯形的上底和下底的和一定,梯形面积与高成正比例。
故答案选:C
【点睛】本题考查梯形的面积公式和正比例的意义。
6.A
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
【详解】因为图上距离÷实际距离=比例尺,所以当比例尺一定,图上距离与实际距离成正比例。
故答案选择A。
【点睛】本题主要考查的是比例尺、正比例和反比例,比例尺=图上距离÷实际距离,解题的关键是判断是否符合正比例的定义,进一步求解。
7. 3∶4 3∶2 正
【分析】第一、二空依据比例的基本性质(在一个比例中,两个外项的积等于两个内项的积)即可解答;第三空依据正比例的意义即可解答。
【详解】(a,b均不为0),那么a∶b=∶=3∶4;
x∶1.5=y(x,y均不为0),那么x∶y=1∶1.5=3∶2;
因为x与y的比值一定,所以x与y成正比例。
【点睛】此题重点考查对比例基本性质和正比例意义的灵活运用。
8.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】知道圆柱的体积,说明它的体积是一定的,圆柱的高×底面积=体积(一定),乘积一定,所以底面积和高成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
9. 正比例 100 90
【分析】此题根据正比例关系的意义或正比例图像特点来解答。我们可以借助图中数据求出流出水的体积与所对应时间的比值,如果两个相关联的量的比值(商)一定,那么这两个量就成正比例关系,(也可以根据图像成一条直线知道成正比例关系)。此时,继而根据求出的比值,即可解答后两个填空。
【详解】(1)观察图形可知:流水5分,水的体积为10升;流水10分,水的体积为20升……10∶5=20∶10=2(一定),因此流出水的体积和时间成正比例关系。
(2)50×2=100(L)
180÷2=90(分)
【点睛】此题考查对正比例意义本质内涵的理解和运用。
10.28
【分析】由题意可知:一根木料锯成4段,需要锯(4-1)次,锯成8段需要锯(8-1)次,锯每次需要的时间一定,则时间与锯的次数成正比,据此即可列比例求解。
【详解】12÷(4-1)×(8-1)
=12÷3×7
=4×7
=28(分钟)
【点睛】本题主要考查植树问题,明确锯每次需要的时间一定,则时间与锯的次数成正比是解题的关键。
11. 反 0
【分析】判断两个相关的量之间成什么比例,就看这两个量是对应比值一定,还是对应乘积一定,如果比值一定,就成正比例;如果乘积一定,就成反比例,据此解答。
【详解】=(x、y均不为0)
xy=5×7
xy=35(一定),x、y成反比例。
xy=35
xy-35=0
【点睛】本题考查正比例、反比例的辨别,根据正比例、反比例意义,进行解答。
12. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
13.正
【分析】根据本数,总价,单价之间的关系;总价÷本数=单价(一定)。即=单价(一定),由此即可判断。
【详解】通过分析可知,总价与本数的比值一定,即本数与总价成正比例。
【点睛】本题主要考查正比例的判断,两个相关联的量的比值一定,即这两个相关联的量成正比例关系。
14.45
【分析】根据题意知道,物体的长度和它的影子的长度的比值- 定,即物体的长度和它的影子的长度的成正比例,由此列式解答即可。
【详解】解:设这座大楼高度约是x米。
1.5∶1=x∶ 30
x=1.5×30
x=45
这座大楼高度约是45米。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】如果,即,是乘积一定,则与成反比例;
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
16.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是乘积一定,如果比值一定,就成正比例,如果乘积一定,则成反比例,据此解答。
【详解】3x=5y,所以x∶y=5∶3=(一定),x和y成正比例。
x和y是两种相关联的量,如果3x=5y,那么x和y成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨别,反比例意义和辨别是解答本题的关键。
17.×
【分析】两个相关联的量,当比值一定时,成正比例关系,据此解答。
【详解】正方形面积=边长×边长;边长= ,比值不一定,所以正方形边长和面积不成正比例。
原题干说法错误。
故答案为:×
【点睛】明确正比例的意义是解答本题的关键。
18.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,就成反比例;据此判断;
【详解】圆的面积公式:面积=π×半径2
面积÷半径2=π(一定),圆的面积与圆的半径的平方成正比例关系。
所以圆的半径和面积不成正比例关系,也不成反比例关系。
原题干说法正确。
故答案为:√
【点睛】熟练掌握圆的面积公式以及正、反比例的意义以及辨识是解答本题的关键。
19.×
【分析】两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的乘积一定时,这两种量叫做成反比例的量,它们的关系叫做反比例关系。据此判断。
【详解】长方形的周长=(长+宽)×2,长方形的周长一定,是指长与宽的和一定,而不是长与宽的积一定,所以长和宽不成反比例关系。
故答案为:×
【点睛】本题主要考查成反比例的意义和识别。注意两个量成反比例关系是这两个量对应数的乘积一定,而不是和一定。
20.x=160;x=50;x=3
【分析】根据等式的性质1,方程左右两边同时加上14.5,根据等式性质2,方程左右两边再同时乘8,可得到方程的解;
先把60%化为小数0.6,方程左边可化简为0.4x=20,根据等式性质2,方程左右两边同时除以0.4,得到方程的解;
根据比例的基本性质,先把比例式转化为乘积式,再根据等式性质2,方程左右两边同时除以,得到方程的解。
【详解】
解:
解:x-0.6x=20
0.4x=20
x=20÷0.4
x=50
解:
21.见详解
【分析】写出实际高度与影长的比,再求出比值即可;要判断实际长度和影长是否成正比例,只需比较它们的比值是不是一定的,即可做出判断。
【详解】2∶0.5
=2÷0.5
=4
1.6∶0.4
=1.6÷0.4
=4
1∶0.25
=1÷0.25
=4
填表如下:
实际长度/m 影长/m 实际长度与影长的比值
竹竿1 2 0.5 4
竹竿2 1.6 0.4 4
木棒 1 0.25 4
通过计算可知:实际长度和影子的比值是4,比值是一定的,所以成正比例。
答:实际长度和影子成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断,进而解决问题。
22.1;1.5;2;2.5
(1)
(2)正;(3)3
【分析】(1)根据图中的数据标出各点,依次连接。
(2)0.5÷1=0.5
1÷2=0.5
1.5÷3=0.5
2÷4=0.5
2.5÷5=0.5
=0.5两个量的比值不变,这两个量成正比例,即可判断。
(3)设聪聪买铅笔花了6元钱,买了12支,明明花的钱是:6÷3=2元,2元钱买了4支笔,12÷4=4,即可解答聪聪买铅笔的支数是明明的几倍。
【详解】(1)
(2) 0.5÷1=0.5
1÷2=0.5
1.5÷3=0.5
2÷4=0.5
2.5÷5=0.5
=0.5,这两个比值不变,根据正比例的性质,比值不变,总价与支数成正比例;
(3)设聪聪买铅笔花6元,买12支铅笔;
明明花的钱数:6÷3=2(元),2元买4支铅笔;
12÷4=3(倍)
【点睛】本田考查正比例性质,根据正比例性质解答实际问题。
23.见详解
【分析】观察图表得到:桃树的行数和每行棵数的积一定,每行的棵数又随着行数的增加或减少而减少或增加。这是两个相反意义的量,故为反比例关系。
【详解】(1)4×30=120;6×20=120;10×12=120,积相等;
(2)这个积表示的实际意义是桃树的总棵数;
(3)桃树的行数和每行棵数是两种相关联的量,每行棵数随着桃树的行数变化而变化,但无论它们怎么变化,相对应的积是一定的,有这样的关系:每行棵数×桃树的行数= 桃树的总棵数(一定),所以桃树的行数和每行的棵数成反比例。
【点睛】此题主要考查学生对反比例关系的理解与判定。
24.252块
【分析】根据客厅的面积一定,一块地砖的面积×地砖的块数=客厅的面积(一定),由此判断一块地砖的面积与地砖的块数成反比例,设出未知数,列出比例解答即可。
【详解】解:设铺满客厅需用x块。
0.16x=0.36×112
x=40.32÷0.16
x=252
答:铺满客厅要用252块。
【点睛】此题考查了反比例的应用,本题注意的是每块地砖的面积×地砖的块数的乘积一定。
25.(1)年龄;身高;
(2)见详解
【分析】(1)表格中有两栏,第一栏是年龄,第二栏是身高,身高随着年龄的变化而变化,这两个都是变化的量。
(2)通过比较年龄及身高数据可知年龄增长,身高也随之增加;据此解答。
【详解】(1)上表中变化的两种量是年龄和身高;
(2)身高随年龄的变化而变化,年龄增长,身高也增加。
【点睛】本题主要考查对数据的分析能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4单元正比例和反比例能力拓展卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.下列各式(a、b均不为0),a和b成反比例的是( )。
A. B. C.
2.下面各题,两种量成正比例关系的是( )。
A.汽车的速度一定,行驶的时间和路程
B.平行四边形面积一定,它的底和高
C.圆的面积与它的半径
3.淘气从家里到学校(路程不变),他行走的时间和行走的速度( )。
A.成正比例 B.成反比例 C.不成比例
4.仔细观察下表,表中相对应的两个量( )。
单价(元) 1 2 3 4 5 6
件数(件) 600 300 200 150 120 100
A.成正比例 B.成反比例 C.不成比例
5.当梯形的( )一定时,梯形的面积与高成正比例。
A.上底 B.下底 C.上、下底之和
6.比例尺一定,图上距离与实际距离成( )。
A.正比例 B.反比例 C.不成比例
二、填空题
7.如果(a,b均不为0),那么a∶b=( )。如果x∶1.5=y(x,y均不为0),那么x∶y=( ),x和y成( )比例。
8.如果知道圆柱的体积,那么圆柱的底面积和高成( )比例。
9.一个水龙头不断地流水,右图表示的是流出水的体积和时间的关系。
(1)从图中可知,流出水的体积和时间成( )关系。
(2)照这样计算,50分流水( )L,要流出180L水,需要( )分。
10.把一根木料锯成4段要用12分钟,照这样,如果锯成8段,一共需要( )分钟。
11.已知(x、y均不为0),则x、y成( )比例,( )。
12.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
13.《童话书》的单价一定,购买的本数与总价成( )比例。
14.同时同地直立在地面上的物体在阳光下的影长与物体高度成正比例。笑笑身高1.5米,她量了旁边大楼影长为30米,此时笑笑的影子长度刚好1米。据此计算出这座大楼高度约是( )米。
三、判断题
15.如果,则与成反比例。( )
16.和是两种相关联的量,如果,那么和成反比例。( )
17.正方形的边长和面积成正比例。( )
18.圆的半径和面积既不成正比例关系也不成反比例关系。( )
19.长方形的周长一定,它的长和宽成反比例关系。( )
四、计算题
20.解方程。
五、解答题
21.天气晴朗的上午,同学们正在操场上测量竹竿、木棒的长度及它们的影长,测量数据如下表。
实际长度/m 影长/m 实际长度与影长的比值
竹竿1 2 0.5
竹竿2 1.6 0.4
木棒 1 0.25
完成表格,比较每次求得的比值,实际长度与影长成正比例吗?
22.铅笔每支0.5元。把下表填完整。
数量/支 1 2 3 4 5 …
总价/元 0.5 1 1.5 2 2.5 …
(1)把铅笔支数与总价所对应的点在图中描述出来,并顺次连接。
(2)总价与支数成( )比例。
(3)聪聪买铅笔花的钱是明明的3倍,聪聪买铅笔的支数是明明的( )倍。
23.果园里种植一批桃树,桃树的行数和每行棵数如下表:
桃树的行数 4 6 10 15 20 …
每行棵数 30 20 12 8 6 …
(1)写出几组相对应的桃树的行数和每行棵数的积。看一看,积相等吗?
(2)这个积表示的实际意义是什么?
(3)桃树的行数和每行的棵数成反比例吗?为什么?
24.小聪家装修客厅,如果用每块面积是0.36平方米的地砖铺地,铺满要用112块;如果改用每块面积是0.16平方米的地砖铺地,铺满客厅要用多少块?
25.下面是小华6~10岁的身高情况统计表。
年龄/岁 6 7 8 9 10
身高/厘米 112 118 125 130 136
(1)上表中有哪两种变化的量?
(2)这两种量是怎样变化的?
参考答案:
1.B
【分析】如果a和b成反比例,则a和b的积一定。据此把各选项的式子进行转化。
【详解】A.,则,a÷b=÷8=(一定),a和b的商一定,则a和b成正比例;
B.,则,ab=3(一定),a和b的积一定,则a和b成反比例;
C.,则2a-b=5,a和b的商和积都不一定,则a和b不成比例。
故答案为:B
【点睛】本题考查反比例的辨认,把原式转化为a和b相乘或相除的形式是解题的关键。
2.A
【分析】两种相关联的量,如果它们对应的比值一定,那么这两个量就成正比例关系。据此选择。
【详解】A.路程÷时间=速度(一定),比值一定,所以汽车的速度一定,行驶的时间和路程成正比例关系。
B.底×高=面积(一定),乘积一定,所以平行四边形面积一定,它的底和高成反比例关系。
C.圆的面积与它的半径不成比例。
故答案为:A
【点睛】此题考查了正比例的辨别,主要看两个量是否是对应的比值一定。
3.B
【分析】两个相关联的量,如果它们对应的比值一定则成正比例关系,如果它们对应的乘积一定,则成反比例关系,据此解答。
【详解】行走的时间×行走的速度=路程(不变),乘积一定,所以成反比例关系。
故答案为:B
【点睛】此题考查了正反比例的辨别,关键看两个量是比值一定还是乘积一定。
4.B
【分析】单价×件数=总价,观察表格发现各种单价下与对应的件数相乘的乘积都是600,据此结合正比例反比例的定义,选出正确选项即可。
【详解】观察表格发现,单价与对应件数的乘积是一定的,所以单价和件数成反比例。
故答案为:B
【点睛】本题考查了正比例和反比例,乘积一定的两个量成反比例,商一定的两个量成正比例。
5.C
【分析】根据梯形的面积公式:梯形面积=(上底+下底)×高÷2,上底+下底的和一定,梯形面积与高成正比例。
【详解】由分析可知,梯形的上底和下底的和一定,梯形面积与高成正比例。
故答案选:C
【点睛】本题考查梯形的面积公式和正比例的意义。
6.A
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
【详解】因为图上距离÷实际距离=比例尺,所以当比例尺一定,图上距离与实际距离成正比例。
故答案选择A。
【点睛】本题主要考查的是比例尺、正比例和反比例,比例尺=图上距离÷实际距离,解题的关键是判断是否符合正比例的定义,进一步求解。
7. 3∶4 3∶2 正
【分析】第一、二空依据比例的基本性质(在一个比例中,两个外项的积等于两个内项的积)即可解答;第三空依据正比例的意义即可解答。
【详解】(a,b均不为0),那么a∶b=∶=3∶4;
x∶1.5=y(x,y均不为0),那么x∶y=1∶1.5=3∶2;
因为x与y的比值一定,所以x与y成正比例。
【点睛】此题重点考查对比例基本性质和正比例意义的灵活运用。
8.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】知道圆柱的体积,说明它的体积是一定的,圆柱的高×底面积=体积(一定),乘积一定,所以底面积和高成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
9. 正比例 100 90
【分析】此题根据正比例关系的意义或正比例图像特点来解答。我们可以借助图中数据求出流出水的体积与所对应时间的比值,如果两个相关联的量的比值(商)一定,那么这两个量就成正比例关系,(也可以根据图像成一条直线知道成正比例关系)。此时,继而根据求出的比值,即可解答后两个填空。
【详解】(1)观察图形可知:流水5分,水的体积为10升;流水10分,水的体积为20升……10∶5=20∶10=2(一定),因此流出水的体积和时间成正比例关系。
(2)50×2=100(L)
180÷2=90(分)
【点睛】此题考查对正比例意义本质内涵的理解和运用。
10.28
【分析】由题意可知:一根木料锯成4段,需要锯(4-1)次,锯成8段需要锯(8-1)次,锯每次需要的时间一定,则时间与锯的次数成正比,据此即可列比例求解。
【详解】12÷(4-1)×(8-1)
=12÷3×7
=4×7
=28(分钟)
【点睛】本题主要考查植树问题,明确锯每次需要的时间一定,则时间与锯的次数成正比是解题的关键。
11. 反 0
【分析】判断两个相关的量之间成什么比例,就看这两个量是对应比值一定,还是对应乘积一定,如果比值一定,就成正比例;如果乘积一定,就成反比例,据此解答。
【详解】=(x、y均不为0)
xy=5×7
xy=35(一定),x、y成反比例。
xy=35
xy-35=0
【点睛】本题考查正比例、反比例的辨别,根据正比例、反比例意义,进行解答。
12. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
13.正
【分析】根据本数,总价,单价之间的关系;总价÷本数=单价(一定)。即=单价(一定),由此即可判断。
【详解】通过分析可知,总价与本数的比值一定,即本数与总价成正比例。
【点睛】本题主要考查正比例的判断,两个相关联的量的比值一定,即这两个相关联的量成正比例关系。
14.45
【分析】根据题意知道,物体的长度和它的影子的长度的比值- 定,即物体的长度和它的影子的长度的成正比例,由此列式解答即可。
【详解】解:设这座大楼高度约是x米。
1.5∶1=x∶ 30
x=1.5×30
x=45
这座大楼高度约是45米。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】如果,即,是乘积一定,则与成反比例;
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
16.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是乘积一定,如果比值一定,就成正比例,如果乘积一定,则成反比例,据此解答。
【详解】3x=5y,所以x∶y=5∶3=(一定),x和y成正比例。
x和y是两种相关联的量,如果3x=5y,那么x和y成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨别,反比例意义和辨别是解答本题的关键。
17.×
【分析】两个相关联的量,当比值一定时,成正比例关系,据此解答。
【详解】正方形面积=边长×边长;边长= ,比值不一定,所以正方形边长和面积不成正比例。
原题干说法错误。
故答案为:×
【点睛】明确正比例的意义是解答本题的关键。
18.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,就成反比例;据此判断;
【详解】圆的面积公式:面积=π×半径2
面积÷半径2=π(一定),圆的面积与圆的半径的平方成正比例关系。
所以圆的半径和面积不成正比例关系,也不成反比例关系。
原题干说法正确。
故答案为:√
【点睛】熟练掌握圆的面积公式以及正、反比例的意义以及辨识是解答本题的关键。
19.×
【分析】两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的乘积一定时,这两种量叫做成反比例的量,它们的关系叫做反比例关系。据此判断。
【详解】长方形的周长=(长+宽)×2,长方形的周长一定,是指长与宽的和一定,而不是长与宽的积一定,所以长和宽不成反比例关系。
故答案为:×
【点睛】本题主要考查成反比例的意义和识别。注意两个量成反比例关系是这两个量对应数的乘积一定,而不是和一定。
20.x=160;x=50;x=3
【分析】根据等式的性质1,方程左右两边同时加上14.5,根据等式性质2,方程左右两边再同时乘8,可得到方程的解;
先把60%化为小数0.6,方程左边可化简为0.4x=20,根据等式性质2,方程左右两边同时除以0.4,得到方程的解;
根据比例的基本性质,先把比例式转化为乘积式,再根据等式性质2,方程左右两边同时除以,得到方程的解。
【详解】
解:
解:x-0.6x=20
0.4x=20
x=20÷0.4
x=50
解:
21.见详解
【分析】写出实际高度与影长的比,再求出比值即可;要判断实际长度和影长是否成正比例,只需比较它们的比值是不是一定的,即可做出判断。
【详解】2∶0.5
=2÷0.5
=4
1.6∶0.4
=1.6÷0.4
=4
1∶0.25
=1÷0.25
=4
填表如下:
实际长度/m 影长/m 实际长度与影长的比值
竹竿1 2 0.5 4
竹竿2 1.6 0.4 4
木棒 1 0.25 4
通过计算可知:实际长度和影子的比值是4,比值是一定的,所以成正比例。
答:实际长度和影子成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断,进而解决问题。
22.1;1.5;2;2.5
(1)
(2)正;(3)3
【分析】(1)根据图中的数据标出各点,依次连接。
(2)0.5÷1=0.5
1÷2=0.5
1.5÷3=0.5
2÷4=0.5
2.5÷5=0.5
=0.5两个量的比值不变,这两个量成正比例,即可判断。
(3)设聪聪买铅笔花了6元钱,买了12支,明明花的钱是:6÷3=2元,2元钱买了4支笔,12÷4=4,即可解答聪聪买铅笔的支数是明明的几倍。
【详解】(1)
(2) 0.5÷1=0.5
1÷2=0.5
1.5÷3=0.5
2÷4=0.5
2.5÷5=0.5
=0.5,这两个比值不变,根据正比例的性质,比值不变,总价与支数成正比例;
(3)设聪聪买铅笔花6元,买12支铅笔;
明明花的钱数:6÷3=2(元),2元买4支铅笔;
12÷4=3(倍)
【点睛】本田考查正比例性质,根据正比例性质解答实际问题。
23.见详解
【分析】观察图表得到:桃树的行数和每行棵数的积一定,每行的棵数又随着行数的增加或减少而减少或增加。这是两个相反意义的量,故为反比例关系。
【详解】(1)4×30=120;6×20=120;10×12=120,积相等;
(2)这个积表示的实际意义是桃树的总棵数;
(3)桃树的行数和每行棵数是两种相关联的量,每行棵数随着桃树的行数变化而变化,但无论它们怎么变化,相对应的积是一定的,有这样的关系:每行棵数×桃树的行数= 桃树的总棵数(一定),所以桃树的行数和每行的棵数成反比例。
【点睛】此题主要考查学生对反比例关系的理解与判定。
24.252块
【分析】根据客厅的面积一定,一块地砖的面积×地砖的块数=客厅的面积(一定),由此判断一块地砖的面积与地砖的块数成反比例,设出未知数,列出比例解答即可。
【详解】解:设铺满客厅需用x块。
0.16x=0.36×112
x=40.32÷0.16
x=252
答:铺满客厅要用252块。
【点睛】此题考查了反比例的应用,本题注意的是每块地砖的面积×地砖的块数的乘积一定。
25.(1)年龄;身高;
(2)见详解
【分析】(1)表格中有两栏,第一栏是年龄,第二栏是身高,身高随着年龄的变化而变化,这两个都是变化的量。
(2)通过比较年龄及身高数据可知年龄增长,身高也随之增加;据此解答。
【详解】(1)上表中变化的两种量是年龄和身高;
(2)身高随年龄的变化而变化,年龄增长,身高也增加。
【点睛】本题主要考查对数据的分析能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
