高三数学复习之第6章 不等式(1-6节)PPT课件-人教版[全套][整理][上学期]
文档属性
| 名称 | 高三数学复习之第6章 不等式(1-6节)PPT课件-人教版[全套][整理][上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-12-20 06:18:00 | ||
图片预览










文档简介
课件57张PPT。第1节 不等式的性质及比较法证明不等式第6章 不等式要点·疑点·考点1.不等式的性质是证明不等式和解不等式的理论基础,通过本节复习,要求理解不等式的性质,会讨论有关不等式命题的充分性和必要性,正确判断命题的真假.
不等式有如下8条性质:
1.a>b? b<a.(反身性)
2.a>b,b>c =>a>c.(传递性)
3.a>b ? a+c>b+c.(平移性)
4.a>b,c>0 => ac>bc;
a>b,c<0 => ac<bc.(伸缩性)
5.a>b≥0 => ,n∈N,且n≥2.(乘方性)
6.a>b≥0 => a>nb,n∈N,且n≥2.(开方性)
7.a>b,c>d => a+c>b+d.(叠加性)
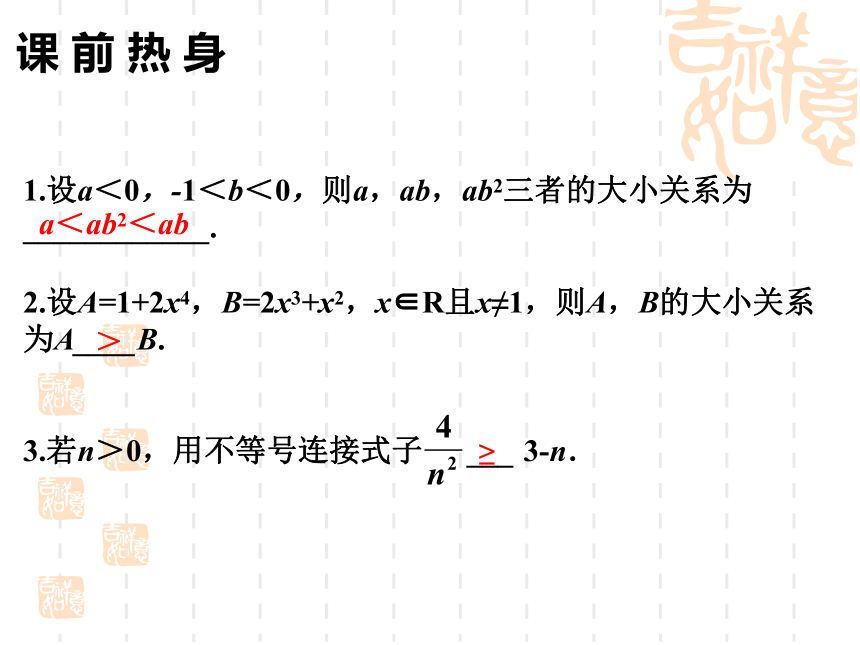
8.a>b≥0,c>d≥0 => ac>bd.(叠乘性) 2.掌握用比较法证明不等式的方法,熟悉它的变形过程.用比较法证明不等式的步骤是:作差——变形——定号.其中的“变形”可以变成平方和,也可以变成因式的积或常数;有关指数式的比较法通常用作商法,步骤是作商——变形——与1比较大小. 1.设a<0,-1<b<0,则a,ab,ab2三者的大小关系为____________.
2.设A=1+2x4,B=2x3+x2,x∈R且x≠1,则A,B的大小关系为A____B.
3.若n>0,用不等号连接式子 ___ 3-n.课 前 热 身a<ab2<ab>≥4.若0<a<1,则下列不等式中正确的是( )
(A)(1-a)(1/3)>(1-a)(1/2)? (B)log(1-a)(1+a)>0
(C)(1-a)3>(1+a)2 (D)(1-a)1+a>1 5.已知三个不等式:①ab>0,②-ca<-db,③bc>ad.以其中两个作条件,余下一个作结论,则可组成___个正确的命题. A3能力·思维·方法1. 比较xn+1+yn+1和xny+xyn(n∈N,x,y∈R+)的大小. 【解题回顾】作差法的关键步骤是差式的变形,常利用因式分解、配方等方法,目的是使差式易于定号,一般四项式的分解常用分组分解法. 2. 设a>0,b>0,求证:【解题回顾】(1)用比较法证明不等式,步骤是:作差(商)——变形——判断符号(与“1”比较);常见的变形手段是通分、因式分解或配方等;常见的变形结果是常数、若干个因式的积或完全平方式等.应注意的是,商比法只适用于两个正数比较大小.
(2)证法2的最后一步中,也可用基本不等式来完成:【解题回顾】在使用放缩技巧时,一定要注意方向,保持一致. 3. 已知x≥0,y≥0,求证: 延伸·拓展【解题回顾】用定义法证明函数的单调性,多用到比较法,特别是作差比较,要切实掌握比较法的推理过程,注意推理的严密性. 4. 设0<a<1,根据函数的单调性定义,证明函数f(x)=logax+
logxa在 上是增函数. 误解分析(1)应变形到最佳形式再判断符号,否则既繁琐又易出错. (2)应熟练掌握对数的性质来判断对数的符号,所以对数性质的应用是解决本题的关键.第2节 用综合法、分析法证明不等式要点·疑点·考点2.综合法的难点在于从何处出发进行论证并不明确,因此我们常常用分析法寻找解题的思路,再用综合法表述.分析法是“执果索因”,综合法是“由因导果”.要注意用分析法证明不等式的表述格式.对于较复杂的不等式的证明,要注意几种方法的综合使用.1.不等式证明的分析法和综合法是从整体上处理不等式的不同形式.分析法的实质是从欲证的不等式出发寻找使之成立的充分条件.综合法是把整个不等式看成一个整体,根据不等式的性质、基本不等式,经过变形、运算,导出欲证的不等式. 3.若 恒成立.则常数a的取值范
围是_________. 1.当a>1,0<b<1时,logab+logba的取值范围是______________. 课 前 热 身(-∞,-2]2.设 ,则函数 的最小值是____,
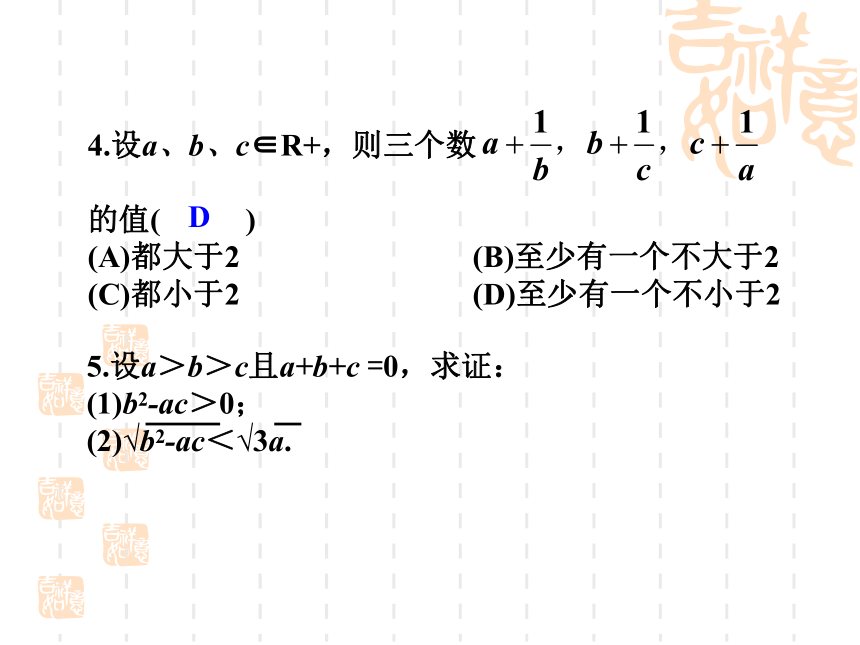
此时x=_______. 4.设a、b、c∈R+,则三个数
的值( )
(A)都大于2 (B)至少有一个不大于2
(C)都小于2 (D)至少有一个不小于2 D能力·思维·方法1.已知a,b,c都是正数,且a≠b,a3-b3=a2-b2,求
证:1<a+b< 【解题回顾】本题证明a+b>1采用了综合法,而证
明a+b< 是采用了分析法.在证题时,从已知条件
出发,实行降幂变换,证出了a+b>1;而从结论出
发,实行升幂变换,导出a+b< .这是两种不同的
思维程序. 【解题回顾】(1)先局部运用基本不等式,再利用不等式的性质(注意限制条件),通过相加(乘)合成为待证的不等式,既是运用基本不等式时的一种重要技能,也是证明不等式时的一种常用方法.
(2)注意条件中1的代换与使用. 2.(1)设a,b,c都是正数,求证:
(2)已知a、b、c∈R+,且a+b+c=1.求证:【解题回顾】利用|a|2=a2(a∈R)是证有关绝对值问题的好方法,证一就是利用这一方法,证二采用的是有理化分子,证三、证四是将数量关系的问题转化为图形的性质问题,充分地考察数学问题的几何背景,常可使问题得以简化. 4.已知a>b>0,求证: 【解题回顾】有趣的是,这个双边不等式,我们能够同时进行证明.延伸·拓展【解题回顾】原不等式从左边到右边的变化是消去a1、a2,因此设法产生a1+a2是变形的目标. 5.设a1,a2∈R+,a1+a2=1,λ1,λ2∈R+,求证:误解分析1.不等式中所含字母较多,分不清它们的关系是出错的主要原因. 2.把握不住证题方向,会导致证题出现混乱. 第3节 算术平均数与几何平均数要点·疑点·考点1.复习并掌握“两个正数的算术平均数不小于它们的几何平均数”的定理.了解它的变式:
(1)a2+b2≥2ab(a,b∈R); (2) (a,b∈R+);
(3) (ab>0); (4) (a,b∈R).
以上各式当且仅当a=b时取等号,并注意各式中字母的取值要求. 2.理解四个“平均数”的大小关系;a,b∈R+,则
.其中当且仅当a=b时取等号.3.在使用“和为常数,积有最大值”和“积为常数,和有最小值”这两个结论时,应把握三点:“一正、二定、三相等、四最值”.当条件不完全具备时,应创造条件. 4.已知两个正数x,y,求x+y与积xy的最值.
(1)xy为定值p,那么当x=y时,x+y有最小值 ;
(2)x+y为定值s,那么当x=y时,积xy有最大值 . 1.“a>0且b>0”是“ ”成立的( )
(A)充分而非必要条件 (B)必要而非充分条件
(C)充要条件 (D)既非充分又非必要条件
2.甲、乙两车从A地沿同一路线到达B地,甲车一半时间的速度为a,另一半时间的速度为b;乙车用速度a行走了一半路程,用速度b行走了另一半路程,若a≠b,则两车到达B地的情况是( )
(A)甲车先到达B地 (B)乙车先到达B地
(C)同时到达 (D)不能判定 课 前 热 身AA4.已知lgx+lgy=1, 的最小值是______. 3.下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)C25.某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
(A)5公里 (B)4公里 (C)3公里 (D)2公里 C能力·思维·方法【解题回顾】三项重新组合成三组后利用基本不等式,是利用基本不等式证明不等式的一种常用技巧.若另加条件a,b,c不全相等,则等号不成立. 1.设a,b,c都是正数,求证:2.(1)若正数x、y满足x+2y=1.求 的最小值;
(2)若x、y∈R+,且2x+8y-xy=0.求x+y的最小值. 【解题回顾】第(1)题常有以下错误解法:
错误的原因在两次运用
平均不等式的时候取等号的条件矛盾.(第一次须x=2y,第二次须x=y).
求条件极值的问题,基本思想是借助条件化二元函数为一元函数,代入法是最基本的方法,代换过程中应密切关注字母隐含的取值范围,也可用三角代换的方法. 3.已知正数a、b满足a+b=1.
(1)求ab的取值范围;(2)求 的最小值. 【解题回顾】用不等式解决有关实际
应用问题,一般先要将实际问题数学
化,建立所求问题的代数式,然后再
据此确定是解不等式,还是用不等式知识求目标函数式的最值. 4.如图,为处理含有某种杂质的矿水,要制造一底宽为2米的无盖长方形沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米,问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A,B孔的面积忽略不计). 【解题回顾】本题应用了命题的等价转化思想,即“如果A是B成立的充要条件,那么B也是A成立的充要条件”. 延伸·拓展误解分析(2)不能把恒成立问题转化成最值问题,变形无方向、易错. (1)不能灵活使用充要条件的概念进行转化,造成证题混乱、易错. 第4节 不等式的解法要点·疑点·考点1.解一元二次不等式是解整式、分式不等式的基础.求解时应首先调整不等式中二次项系数a ,使a>0.在熟练掌握一元一次不等式(组)和一元二次不等式解法的基础上,掌握分式不等 式、简单的高次不等式的解法.?
2.掌握利用图形、数轴讨论不等式组解集的方法.?
3.讨论一元二次不等式系数中的字母取值问题,常用到分解因式、判别式、求根公式、韦达 定理,还应充分考虑运用函数思想.课 前 热 身 1.不等式(2/x)<x+1的解集为___________________.{x|x>1或-2<x<0}2.已知函数f(x)=x2+ax+3,当x∈[-2,2]时,不等式f(x)>a恒成立,求a的取值范围是_________________-7 <a<2 3.不等式((x-2)2(x-3))/(x+1)<0的解集为?
__________________________.?
{x|-1<x<2或2<x<3}4.不等式ax/(x-1)<1的解集为{x|x<1或x>2},则
a=( )
(A)2 (B)-2 (C)12 (D)-12
? 5.已知不等式①x2-4x+3<0,②x2-6x+8<0,③2x2-9x+m<0,要使同时满足①、②的x也满 足③,则有( )?
(A)m>9 (B)m=9? (C)m<9 (D)0<m≤9?C ?
C能力·思维·方法 1.设m∈R,解关于x的不等式m2x2+2mx-3<0.? 【解题回顾】解此不等式时,由于m∈R,因此不能完全按一元二次不等式的解法求解.因 为当m=0时,原不等式化为-3<0,此时不等式的解集为R,所以解题时应分m=0与m≠0两种 情况来讨论.?
在解出m2x2+2mx-3=0的两根为x1=-3/m,x2=1/m后,认为-3/m<1/m也是易出现的错误之处.这 时也应分情况来讨论:当m>0时,-3/m<1/m;当m<0时,-3/m>1/m.? 2.解下列不等式:? (1)(x+2)(x+1)2(x-1)(x-2)≤0;? (2)(x2+2x-2)/(3+2x-x2)<x. 【解题回顾】题(1)是解高次不等式,一般解法为通过同解变形,使一边为0,另一边为一 次因式的积(x的系数为正),然后用根轴法求解.如果出现重因式(x-a)n,n为奇数,该式可 视为(x-a)来求解.若n为偶数,则先将该式去掉,最后再讨论x=a是否为原不等式的解.? 题(2)是解分式不等式,不可盲目去分母,一般解法是:移项,通分,分解因式后化为f(x)/g (x)>0? f(x)·? g(x)>0,用序轴标根法解,若f(x)/g(x)≥0,则f(x)·g(x)≥0且g(x)≠0.3.已知两个命题:p:当x∈[1,+∞)时,函数f(x)=
(0<a<1)恒有意义;q:关于x的 不等式|x2-2x-3|≥(1-5/(m+1))的解集为实数集R;如果这两个命题中有且只有一个是真命题, 试求m的取值范围.? 【解题回顾】本题两个命题的设计均为恒成立问题,都可以转化为最值问题得到相关的不等 式,注意对两个命题进行讨论以满足条件,从而得到m的范围.? 4.解关于x的不等式(k(1-x))/(x-2) +1<0(k≠1,且k≠0).?【解题回顾】本题是含参数的分式不等式的求解.首先要通分,变形成因式积的形式,再 由判断根的大小来确定讨论的标准与范围.延伸·拓展5.设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α,β为何实数,恒有f(sin α)≥0,且 f(2+cos β)≤0.? (1)求证:b+c=-1;(2)求c的取值范围;(3)若函数? f(sin α)的最大值为8,求b,c的值.? 【解题回顾】本题充分体现了二次函数与二次不等式的联系与转化,其解法“巧”在利用 条件的特殊状态求出f(1)=0,“活”在二次函数向不等式的转化,“妙”在利用二次函数 单调性确定最大值的表达式,进而求出b,c.? 1?不能充分使用二次函数与二次不等式之间的关系.?
2?不能利用二次函数单调性,求给定区间上的二次函数的最值,致使建立错误的关系.同时 注意与前面小题中的结论相结合.误解分析第5节 不等式的解法要点·疑点·考点1.掌握无理不等式的解法.
解的过程注意两点:
(1)保证根式有意义;
(2)在利用平方去掉根号时,不等式两边要为非负值. 2.掌握绝对值不等式的解法.最简绝对值不等式分两类:
(1)|f(x)|≥a(a>0)等价于f(x)≤-a或f(x)≥a;
(2)|f(x)|≤a(a>0)等价于-a≤f(x)≤a. 3.掌握指数、对数不等式的基本解法——基本型(ax>b,logax>b),同底型(af(x)>ag(x)、logaf(x)>logag(x)),或利用换元法或通过函数的单调性将其转化为代数不等式.转化过程中,应充分关注函数定义域,保证变形的同解性.在转化为不等式组的解时,应注意区别“且”、“或”,涉及到最后几个不等式的解集是“交”还是“并”. 1.方程 的解集是( )
(A)(-1,0)∪(3,+∞) (B)(-∞,-1)∪(0,3)
(C)(-1,0]∪[3,+∞) (D)(-∞,-1)∪[0,3] 课 前 热 身C3.不等式 的解集为_____________ 2.x∈{x|g(x)≤f(x)≤h(x)}是x∈{x|[f(x)-h(x)][(f(x)-g(x))]≤0}的( )?
(A)充分不必要条件? (B)必要不充分条件?
(C)充要条件? (D)既非充分也非必要条件?A? 4.关于x的不等式x3+13a2x>5ax2+9a3的解集是
___________________
? 5.方程x2-3mx+m=0的一个根大于0且小于1,另一个根大于1且小于2,则m的取值范围是_________________.{x|x>a}?
{m|1/2 <m<4/5}能力·思维·方法1.解不等式2.已知关于x的不等式(ax-5)/(x2-a)<0的解集为M.? (1)当a=4时,求集合M;?
(2)若3∈M,且5?M.求实数a的取值范围.【解题回顾】 (1)解分式不等式常用序轴标根法,(2)3∈M,所以3是不等式的解,也即满 足不等式,5?M,所以5不是不等式的解,则5在M补集中,本题易把25-a=0丢掉.3.已知a>0,不等式|x-4|+|x-3|<a在实数集R上的解集不是空集,求a的取值范围. 【解题回顾】此题所用的构造函数及数形结合的方法,是行之有效的常用方法. 变题1 若不等式|x-4|+|x-3|>a对于一切实数x恒成立,求a的取值范围. 变题2 若不等式|x-4|-|x-3|<a的解集在R上不是空集.求a的取值范围. 变题3 不等式|x-4|-|x-3|>a在R上恒成立,求a的取值范围. 延伸·拓展【解题回顾】本题亦为含有参数的不等式,但不是常见的就参数的取值讨论不等式的解,而是就不等式成立这一结论,去研究参数的范围.两者各尽其妙,不可偏废.此外,通过本题,可培养学生研究问题的意识、方法与习惯,应予关注. 5.一位同学写了一个不等式:
(1)他发现当c=1、2、3时不等式都成立,试问:不等式是否对任意的正数c都成立?为什么?
(2)对于已知的正数c,这位同学还发现,把不等式右边的
“ ”改成某些值,如-c,0等,不等式总是成立的,试求
出所有这些值的集合M. (1)直接作差,造成运算量较大,容易出现错误. 误解分析(2)在运用基本不等式时,不考虑等号是否取得.即不讨论c的取值范围,致使结果不全. 第6节 不等式的综合应用要点·疑点·考点1.近几年的高考试题中,不等式的应用已渗透到函数、三角、数列、解析几何、立体几何等内容中,涉及的深度、范围也在提高和增大,体现了不等式内容的重要性、思想方法的独特性.既有一般的解不等式(组)和证明不等式的题,也有将其作为数学工具应用的试题. 2.本课时的重点是通过不等式应用的复习,提高综合运用各种数学知识的能力,以及通过建立不等式模型解应用题,提高分析问题和解决问题的能力.
不等式的应用是不等式的重点内容,它在中学数学有着广泛的应用,主要表现在:
(1)求函数的定义域、值域;
(2)求函数的最值;
(3)讨论函数的单调性;
(4)研究方程的实根分布;
(5)求参数的取值范围;
(6)解决与不等式有关的应用题. 3.用题中有一类是寻找最优化结果的,通常是把问题转化为不等式表示的模型,再求出极值. 课 前 热 身1.如果函数y=log(1/3)(x2-2ax+a+2)的单调递增区间是(-∞,a],那么实数a的取值范围是__________. -1<a<2B3.若关于x的方程9x+(4+a)·3x+4=0有解,则实数a的取值范围是( )
(A)(-∞,-8]∪[0,+∞) (B)(-∞,-4)
(C)[-8,4) (D)(-∞ ,-8] D4. 设a,b,c∈R,ab=2且c≤a2+b2恒成立,则c的最大值为______. 45.不等式ax2-bx+c>0的解集是(-1/2,2),对于a、b、c有以下结论:①a>0;②b>0;③c>0;④a+b+c>0;⑤a-b+c>0.其中正确结论的序号是__________③、⑤能力·思维·方法1.已知实数α,β,γ满足α+β+γ>0,αβ+βγ+γα>0,αβγ>0,证明α,β, γ都大于0.【解题回顾】 (1)等比数列的前n项求和公式的运用时注意公比q的讨论.? (2)第2小题是从Tn中变形出Sn,利用(1)中Sn>0可简化运算,再转化为求函数的最值问题. ?3.若抛物线c:y=ax2-1上总存在关于直线l:x+y=0对称的两点,试求实数a的取值范围. ?
【解题分析】求a的取值范围,关键是设法导出a的不等式.可考虑由判别式导出不等式.2.已知等比数列{an}的首项a1>0,公比q>-1,且q≠1,前n项和为Sn;在数列{bn}中,bn=an+1-kan+2,前n项和为Tn.
(1)求证:Sn>0;
(2)证明若Tn>kSn对一切正整数n成立,则k≤-1/2. 【解题回顾】(1)等比数列的前n项求和公式的运用时注意公比q的讨论.
(2)第2小题是从Tn中变形出Sn,利用(1)中Sn>0可简化运算,再转化为求函数的最值问题. 3. 若抛物线c:y=ax2-1上总存在关于直线l:x+y=0成轴对称的两点,试求实数a的取值范围. 【解题回顾】上面的解法是由判别式导出a的不等式的,本题还可以由均值不等式或由点与曲线的位置关系导出a的不等式. 【解题回顾】(1)本小题是利用x+1/x与x2+1/x2,x4+1/x4之间的关系用配凑法求得.
(2)通过换元,利用一元二次方程的实根分布知识求解.
(3)把恒成立问题转化为求函数的最值,本题利用函数的单调性求最大值. 4.设x=logst+logts,y=logs4t+logt4s+m(logs2t+logt2s),其中,s>1,t>1,m∈R.
(1)将y表示成x的函数y=f(x),并求f(x)的定义域;
(2)若关于x的方程f(x)=0,有且仅有一个实数根,求m的取值范围;
(3)若f(x)>0恒成立,求m的取值范围. 延伸·拓展【解题回顾】本题是函数与不等式的综合题,对于(3)是已知两参数a、x的范围,求另一参数m的范围.此类题的做法是先消去一参x,后求m范围. 5.已知f(x)是定义在[-1,1]上的奇函数,且 f(1)=1,若
a,b∈[-1,1],a+b≠0有
(1)判断函数f(x)在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式
(3)若f(x)≤m2-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围. 误解分析 不等式问题大多需要“等价转化”,而能否确保转化“等价”是解题成败的关键.
不等式有如下8条性质:
1.a>b? b<a.(反身性)
2.a>b,b>c =>a>c.(传递性)
3.a>b ? a+c>b+c.(平移性)
4.a>b,c>0 => ac>bc;
a>b,c<0 => ac<bc.(伸缩性)
5.a>b≥0 => ,n∈N,且n≥2.(乘方性)
6.a>b≥0 => a>nb,n∈N,且n≥2.(开方性)
7.a>b,c>d => a+c>b+d.(叠加性)
8.a>b≥0,c>d≥0 => ac>bd.(叠乘性) 2.掌握用比较法证明不等式的方法,熟悉它的变形过程.用比较法证明不等式的步骤是:作差——变形——定号.其中的“变形”可以变成平方和,也可以变成因式的积或常数;有关指数式的比较法通常用作商法,步骤是作商——变形——与1比较大小. 1.设a<0,-1<b<0,则a,ab,ab2三者的大小关系为____________.
2.设A=1+2x4,B=2x3+x2,x∈R且x≠1,则A,B的大小关系为A____B.
3.若n>0,用不等号连接式子 ___ 3-n.课 前 热 身a<ab2<ab>≥4.若0<a<1,则下列不等式中正确的是( )
(A)(1-a)(1/3)>(1-a)(1/2)? (B)log(1-a)(1+a)>0
(C)(1-a)3>(1+a)2 (D)(1-a)1+a>1 5.已知三个不等式:①ab>0,②-ca<-db,③bc>ad.以其中两个作条件,余下一个作结论,则可组成___个正确的命题. A3能力·思维·方法1. 比较xn+1+yn+1和xny+xyn(n∈N,x,y∈R+)的大小. 【解题回顾】作差法的关键步骤是差式的变形,常利用因式分解、配方等方法,目的是使差式易于定号,一般四项式的分解常用分组分解法. 2. 设a>0,b>0,求证:【解题回顾】(1)用比较法证明不等式,步骤是:作差(商)——变形——判断符号(与“1”比较);常见的变形手段是通分、因式分解或配方等;常见的变形结果是常数、若干个因式的积或完全平方式等.应注意的是,商比法只适用于两个正数比较大小.
(2)证法2的最后一步中,也可用基本不等式来完成:【解题回顾】在使用放缩技巧时,一定要注意方向,保持一致. 3. 已知x≥0,y≥0,求证: 延伸·拓展【解题回顾】用定义法证明函数的单调性,多用到比较法,特别是作差比较,要切实掌握比较法的推理过程,注意推理的严密性. 4. 设0<a<1,根据函数的单调性定义,证明函数f(x)=logax+
logxa在 上是增函数. 误解分析(1)应变形到最佳形式再判断符号,否则既繁琐又易出错. (2)应熟练掌握对数的性质来判断对数的符号,所以对数性质的应用是解决本题的关键.第2节 用综合法、分析法证明不等式要点·疑点·考点2.综合法的难点在于从何处出发进行论证并不明确,因此我们常常用分析法寻找解题的思路,再用综合法表述.分析法是“执果索因”,综合法是“由因导果”.要注意用分析法证明不等式的表述格式.对于较复杂的不等式的证明,要注意几种方法的综合使用.1.不等式证明的分析法和综合法是从整体上处理不等式的不同形式.分析法的实质是从欲证的不等式出发寻找使之成立的充分条件.综合法是把整个不等式看成一个整体,根据不等式的性质、基本不等式,经过变形、运算,导出欲证的不等式. 3.若 恒成立.则常数a的取值范
围是_________. 1.当a>1,0<b<1时,logab+logba的取值范围是______________. 课 前 热 身(-∞,-2]2.设 ,则函数 的最小值是____,
此时x=_______. 4.设a、b、c∈R+,则三个数
的值( )
(A)都大于2 (B)至少有一个不大于2
(C)都小于2 (D)至少有一个不小于2 D能力·思维·方法1.已知a,b,c都是正数,且a≠b,a3-b3=a2-b2,求
证:1<a+b< 【解题回顾】本题证明a+b>1采用了综合法,而证
明a+b< 是采用了分析法.在证题时,从已知条件
出发,实行降幂变换,证出了a+b>1;而从结论出
发,实行升幂变换,导出a+b< .这是两种不同的
思维程序. 【解题回顾】(1)先局部运用基本不等式,再利用不等式的性质(注意限制条件),通过相加(乘)合成为待证的不等式,既是运用基本不等式时的一种重要技能,也是证明不等式时的一种常用方法.
(2)注意条件中1的代换与使用. 2.(1)设a,b,c都是正数,求证:
(2)已知a、b、c∈R+,且a+b+c=1.求证:【解题回顾】利用|a|2=a2(a∈R)是证有关绝对值问题的好方法,证一就是利用这一方法,证二采用的是有理化分子,证三、证四是将数量关系的问题转化为图形的性质问题,充分地考察数学问题的几何背景,常可使问题得以简化. 4.已知a>b>0,求证: 【解题回顾】有趣的是,这个双边不等式,我们能够同时进行证明.延伸·拓展【解题回顾】原不等式从左边到右边的变化是消去a1、a2,因此设法产生a1+a2是变形的目标. 5.设a1,a2∈R+,a1+a2=1,λ1,λ2∈R+,求证:误解分析1.不等式中所含字母较多,分不清它们的关系是出错的主要原因. 2.把握不住证题方向,会导致证题出现混乱. 第3节 算术平均数与几何平均数要点·疑点·考点1.复习并掌握“两个正数的算术平均数不小于它们的几何平均数”的定理.了解它的变式:
(1)a2+b2≥2ab(a,b∈R); (2) (a,b∈R+);
(3) (ab>0); (4) (a,b∈R).
以上各式当且仅当a=b时取等号,并注意各式中字母的取值要求. 2.理解四个“平均数”的大小关系;a,b∈R+,则
.其中当且仅当a=b时取等号.3.在使用“和为常数,积有最大值”和“积为常数,和有最小值”这两个结论时,应把握三点:“一正、二定、三相等、四最值”.当条件不完全具备时,应创造条件. 4.已知两个正数x,y,求x+y与积xy的最值.
(1)xy为定值p,那么当x=y时,x+y有最小值 ;
(2)x+y为定值s,那么当x=y时,积xy有最大值 . 1.“a>0且b>0”是“ ”成立的( )
(A)充分而非必要条件 (B)必要而非充分条件
(C)充要条件 (D)既非充分又非必要条件
2.甲、乙两车从A地沿同一路线到达B地,甲车一半时间的速度为a,另一半时间的速度为b;乙车用速度a行走了一半路程,用速度b行走了另一半路程,若a≠b,则两车到达B地的情况是( )
(A)甲车先到达B地 (B)乙车先到达B地
(C)同时到达 (D)不能判定 课 前 热 身AA4.已知lgx+lgy=1, 的最小值是______. 3.下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)C25.某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
(A)5公里 (B)4公里 (C)3公里 (D)2公里 C能力·思维·方法【解题回顾】三项重新组合成三组后利用基本不等式,是利用基本不等式证明不等式的一种常用技巧.若另加条件a,b,c不全相等,则等号不成立. 1.设a,b,c都是正数,求证:2.(1)若正数x、y满足x+2y=1.求 的最小值;
(2)若x、y∈R+,且2x+8y-xy=0.求x+y的最小值. 【解题回顾】第(1)题常有以下错误解法:
错误的原因在两次运用
平均不等式的时候取等号的条件矛盾.(第一次须x=2y,第二次须x=y).
求条件极值的问题,基本思想是借助条件化二元函数为一元函数,代入法是最基本的方法,代换过程中应密切关注字母隐含的取值范围,也可用三角代换的方法. 3.已知正数a、b满足a+b=1.
(1)求ab的取值范围;(2)求 的最小值. 【解题回顾】用不等式解决有关实际
应用问题,一般先要将实际问题数学
化,建立所求问题的代数式,然后再
据此确定是解不等式,还是用不等式知识求目标函数式的最值. 4.如图,为处理含有某种杂质的矿水,要制造一底宽为2米的无盖长方形沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米,问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A,B孔的面积忽略不计). 【解题回顾】本题应用了命题的等价转化思想,即“如果A是B成立的充要条件,那么B也是A成立的充要条件”. 延伸·拓展误解分析(2)不能把恒成立问题转化成最值问题,变形无方向、易错. (1)不能灵活使用充要条件的概念进行转化,造成证题混乱、易错. 第4节 不等式的解法要点·疑点·考点1.解一元二次不等式是解整式、分式不等式的基础.求解时应首先调整不等式中二次项系数a ,使a>0.在熟练掌握一元一次不等式(组)和一元二次不等式解法的基础上,掌握分式不等 式、简单的高次不等式的解法.?
2.掌握利用图形、数轴讨论不等式组解集的方法.?
3.讨论一元二次不等式系数中的字母取值问题,常用到分解因式、判别式、求根公式、韦达 定理,还应充分考虑运用函数思想.课 前 热 身 1.不等式(2/x)<x+1的解集为___________________.{x|x>1或-2<x<0}2.已知函数f(x)=x2+ax+3,当x∈[-2,2]时,不等式f(x)>a恒成立,求a的取值范围是_________________-7 <a<2 3.不等式((x-2)2(x-3))/(x+1)<0的解集为?
__________________________.?
{x|-1<x<2或2<x<3}4.不等式ax/(x-1)<1的解集为{x|x<1或x>2},则
a=( )
(A)2 (B)-2 (C)12 (D)-12
? 5.已知不等式①x2-4x+3<0,②x2-6x+8<0,③2x2-9x+m<0,要使同时满足①、②的x也满 足③,则有( )?
(A)m>9 (B)m=9? (C)m<9 (D)0<m≤9?C ?
C能力·思维·方法 1.设m∈R,解关于x的不等式m2x2+2mx-3<0.? 【解题回顾】解此不等式时,由于m∈R,因此不能完全按一元二次不等式的解法求解.因 为当m=0时,原不等式化为-3<0,此时不等式的解集为R,所以解题时应分m=0与m≠0两种 情况来讨论.?
在解出m2x2+2mx-3=0的两根为x1=-3/m,x2=1/m后,认为-3/m<1/m也是易出现的错误之处.这 时也应分情况来讨论:当m>0时,-3/m<1/m;当m<0时,-3/m>1/m.? 2.解下列不等式:? (1)(x+2)(x+1)2(x-1)(x-2)≤0;? (2)(x2+2x-2)/(3+2x-x2)<x. 【解题回顾】题(1)是解高次不等式,一般解法为通过同解变形,使一边为0,另一边为一 次因式的积(x的系数为正),然后用根轴法求解.如果出现重因式(x-a)n,n为奇数,该式可 视为(x-a)来求解.若n为偶数,则先将该式去掉,最后再讨论x=a是否为原不等式的解.? 题(2)是解分式不等式,不可盲目去分母,一般解法是:移项,通分,分解因式后化为f(x)/g (x)>0? f(x)·? g(x)>0,用序轴标根法解,若f(x)/g(x)≥0,则f(x)·g(x)≥0且g(x)≠0.3.已知两个命题:p:当x∈[1,+∞)时,函数f(x)=
(0<a<1)恒有意义;q:关于x的 不等式|x2-2x-3|≥(1-5/(m+1))的解集为实数集R;如果这两个命题中有且只有一个是真命题, 试求m的取值范围.? 【解题回顾】本题两个命题的设计均为恒成立问题,都可以转化为最值问题得到相关的不等 式,注意对两个命题进行讨论以满足条件,从而得到m的范围.? 4.解关于x的不等式(k(1-x))/(x-2) +1<0(k≠1,且k≠0).?【解题回顾】本题是含参数的分式不等式的求解.首先要通分,变形成因式积的形式,再 由判断根的大小来确定讨论的标准与范围.延伸·拓展5.设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α,β为何实数,恒有f(sin α)≥0,且 f(2+cos β)≤0.? (1)求证:b+c=-1;(2)求c的取值范围;(3)若函数? f(sin α)的最大值为8,求b,c的值.? 【解题回顾】本题充分体现了二次函数与二次不等式的联系与转化,其解法“巧”在利用 条件的特殊状态求出f(1)=0,“活”在二次函数向不等式的转化,“妙”在利用二次函数 单调性确定最大值的表达式,进而求出b,c.? 1?不能充分使用二次函数与二次不等式之间的关系.?
2?不能利用二次函数单调性,求给定区间上的二次函数的最值,致使建立错误的关系.同时 注意与前面小题中的结论相结合.误解分析第5节 不等式的解法要点·疑点·考点1.掌握无理不等式的解法.
解的过程注意两点:
(1)保证根式有意义;
(2)在利用平方去掉根号时,不等式两边要为非负值. 2.掌握绝对值不等式的解法.最简绝对值不等式分两类:
(1)|f(x)|≥a(a>0)等价于f(x)≤-a或f(x)≥a;
(2)|f(x)|≤a(a>0)等价于-a≤f(x)≤a. 3.掌握指数、对数不等式的基本解法——基本型(ax>b,logax>b),同底型(af(x)>ag(x)、logaf(x)>logag(x)),或利用换元法或通过函数的单调性将其转化为代数不等式.转化过程中,应充分关注函数定义域,保证变形的同解性.在转化为不等式组的解时,应注意区别“且”、“或”,涉及到最后几个不等式的解集是“交”还是“并”. 1.方程 的解集是( )
(A)(-1,0)∪(3,+∞) (B)(-∞,-1)∪(0,3)
(C)(-1,0]∪[3,+∞) (D)(-∞,-1)∪[0,3] 课 前 热 身C3.不等式 的解集为_____________ 2.x∈{x|g(x)≤f(x)≤h(x)}是x∈{x|[f(x)-h(x)][(f(x)-g(x))]≤0}的( )?
(A)充分不必要条件? (B)必要不充分条件?
(C)充要条件? (D)既非充分也非必要条件?A? 4.关于x的不等式x3+13a2x>5ax2+9a3的解集是
___________________
? 5.方程x2-3mx+m=0的一个根大于0且小于1,另一个根大于1且小于2,则m的取值范围是_________________.{x|x>a}?
{m|1/2 <m<4/5}能力·思维·方法1.解不等式2.已知关于x的不等式(ax-5)/(x2-a)<0的解集为M.? (1)当a=4时,求集合M;?
(2)若3∈M,且5?M.求实数a的取值范围.【解题回顾】 (1)解分式不等式常用序轴标根法,(2)3∈M,所以3是不等式的解,也即满 足不等式,5?M,所以5不是不等式的解,则5在M补集中,本题易把25-a=0丢掉.3.已知a>0,不等式|x-4|+|x-3|<a在实数集R上的解集不是空集,求a的取值范围. 【解题回顾】此题所用的构造函数及数形结合的方法,是行之有效的常用方法. 变题1 若不等式|x-4|+|x-3|>a对于一切实数x恒成立,求a的取值范围. 变题2 若不等式|x-4|-|x-3|<a的解集在R上不是空集.求a的取值范围. 变题3 不等式|x-4|-|x-3|>a在R上恒成立,求a的取值范围. 延伸·拓展【解题回顾】本题亦为含有参数的不等式,但不是常见的就参数的取值讨论不等式的解,而是就不等式成立这一结论,去研究参数的范围.两者各尽其妙,不可偏废.此外,通过本题,可培养学生研究问题的意识、方法与习惯,应予关注. 5.一位同学写了一个不等式:
(1)他发现当c=1、2、3时不等式都成立,试问:不等式是否对任意的正数c都成立?为什么?
(2)对于已知的正数c,这位同学还发现,把不等式右边的
“ ”改成某些值,如-c,0等,不等式总是成立的,试求
出所有这些值的集合M. (1)直接作差,造成运算量较大,容易出现错误. 误解分析(2)在运用基本不等式时,不考虑等号是否取得.即不讨论c的取值范围,致使结果不全. 第6节 不等式的综合应用要点·疑点·考点1.近几年的高考试题中,不等式的应用已渗透到函数、三角、数列、解析几何、立体几何等内容中,涉及的深度、范围也在提高和增大,体现了不等式内容的重要性、思想方法的独特性.既有一般的解不等式(组)和证明不等式的题,也有将其作为数学工具应用的试题. 2.本课时的重点是通过不等式应用的复习,提高综合运用各种数学知识的能力,以及通过建立不等式模型解应用题,提高分析问题和解决问题的能力.
不等式的应用是不等式的重点内容,它在中学数学有着广泛的应用,主要表现在:
(1)求函数的定义域、值域;
(2)求函数的最值;
(3)讨论函数的单调性;
(4)研究方程的实根分布;
(5)求参数的取值范围;
(6)解决与不等式有关的应用题. 3.用题中有一类是寻找最优化结果的,通常是把问题转化为不等式表示的模型,再求出极值. 课 前 热 身1.如果函数y=log(1/3)(x2-2ax+a+2)的单调递增区间是(-∞,a],那么实数a的取值范围是__________. -1<a<2B3.若关于x的方程9x+(4+a)·3x+4=0有解,则实数a的取值范围是( )
(A)(-∞,-8]∪[0,+∞) (B)(-∞,-4)
(C)[-8,4) (D)(-∞ ,-8] D4. 设a,b,c∈R,ab=2且c≤a2+b2恒成立,则c的最大值为______. 45.不等式ax2-bx+c>0的解集是(-1/2,2),对于a、b、c有以下结论:①a>0;②b>0;③c>0;④a+b+c>0;⑤a-b+c>0.其中正确结论的序号是__________③、⑤能力·思维·方法1.已知实数α,β,γ满足α+β+γ>0,αβ+βγ+γα>0,αβγ>0,证明α,β, γ都大于0.【解题回顾】 (1)等比数列的前n项求和公式的运用时注意公比q的讨论.? (2)第2小题是从Tn中变形出Sn,利用(1)中Sn>0可简化运算,再转化为求函数的最值问题. ?3.若抛物线c:y=ax2-1上总存在关于直线l:x+y=0对称的两点,试求实数a的取值范围. ?
【解题分析】求a的取值范围,关键是设法导出a的不等式.可考虑由判别式导出不等式.2.已知等比数列{an}的首项a1>0,公比q>-1,且q≠1,前n项和为Sn;在数列{bn}中,bn=an+1-kan+2,前n项和为Tn.
(1)求证:Sn>0;
(2)证明若Tn>kSn对一切正整数n成立,则k≤-1/2. 【解题回顾】(1)等比数列的前n项求和公式的运用时注意公比q的讨论.
(2)第2小题是从Tn中变形出Sn,利用(1)中Sn>0可简化运算,再转化为求函数的最值问题. 3. 若抛物线c:y=ax2-1上总存在关于直线l:x+y=0成轴对称的两点,试求实数a的取值范围. 【解题回顾】上面的解法是由判别式导出a的不等式的,本题还可以由均值不等式或由点与曲线的位置关系导出a的不等式. 【解题回顾】(1)本小题是利用x+1/x与x2+1/x2,x4+1/x4之间的关系用配凑法求得.
(2)通过换元,利用一元二次方程的实根分布知识求解.
(3)把恒成立问题转化为求函数的最值,本题利用函数的单调性求最大值. 4.设x=logst+logts,y=logs4t+logt4s+m(logs2t+logt2s),其中,s>1,t>1,m∈R.
(1)将y表示成x的函数y=f(x),并求f(x)的定义域;
(2)若关于x的方程f(x)=0,有且仅有一个实数根,求m的取值范围;
(3)若f(x)>0恒成立,求m的取值范围. 延伸·拓展【解题回顾】本题是函数与不等式的综合题,对于(3)是已知两参数a、x的范围,求另一参数m的范围.此类题的做法是先消去一参x,后求m范围. 5.已知f(x)是定义在[-1,1]上的奇函数,且 f(1)=1,若
a,b∈[-1,1],a+b≠0有
(1)判断函数f(x)在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式
(3)若f(x)≤m2-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围. 误解分析 不等式问题大多需要“等价转化”,而能否确保转化“等价”是解题成败的关键.
