《 1.4.2用空间向量研究距离、夹角问题》说课课件(共18张PPT)
文档属性
| 名称 | 《 1.4.2用空间向量研究距离、夹角问题》说课课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 114.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 19:47:09 | ||
图片预览



文档简介
(共18张PPT)
《用空间向量研究距离、夹角问题》说课
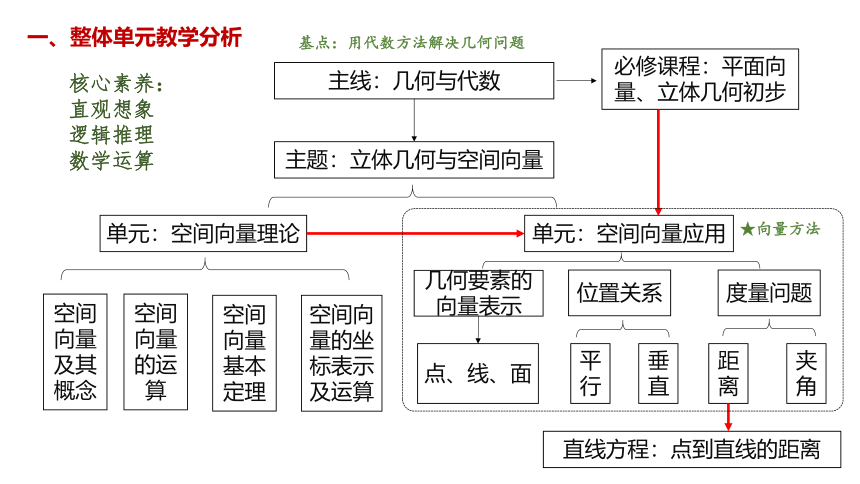
一、整体单元教学分析
主线:几何与代数
主题:立体几何与空间向量
单元:空间向量理论
必修课程:平面向量、立体几何初步
单元:空间向量应用
基点:用代数方法解决几何问题
空间向量及其概念
空间向量的运算
空间向量基本定理
空间向量的坐标表示及运算
位置关系
度量问题
平行
垂直
距离
夹角
直线方程:点到直线的距离
★向量方法
几何要素的向量表示
点、线、面
核心素养:
直观想象
逻辑推理
数学运算
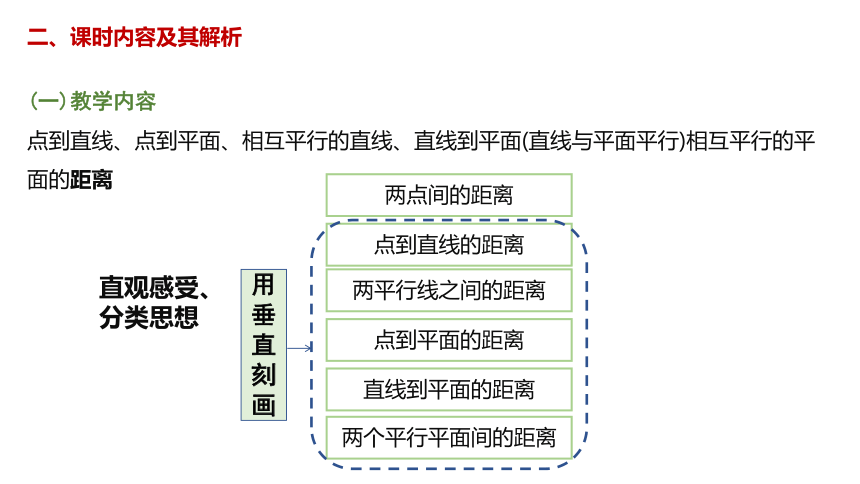
二、课时内容及其解析
(一)教学内容
点到直线、点到平面、相互平行的直线、直线到平面(直线与平面平行)相互平行的平面的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两个平行平面间的距离
用垂直刻画
直观感受、
分类思想
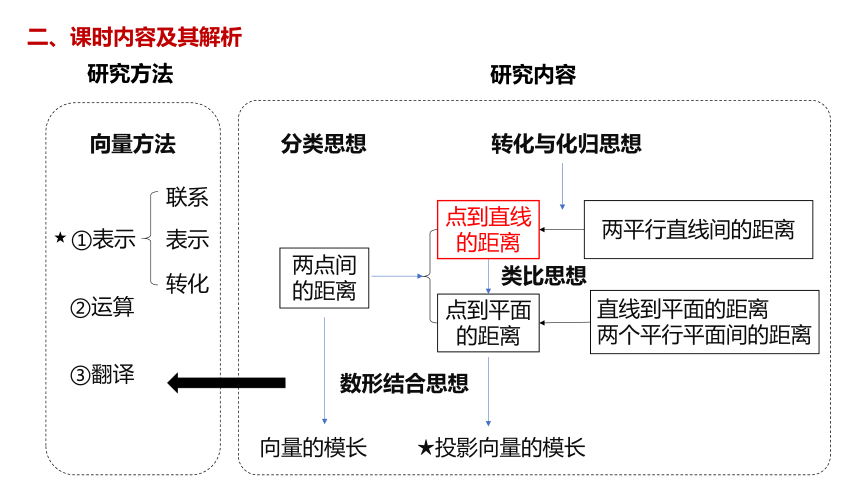
点到平面的距离
两平行直线间的距离
直线到平面的距离
两个平行平面间的距离
点到直线的距离
两点间的距离
转化与化归思想
分类思想
向量的模长
★投影向量的模长
向量方法
①表示
②运算
③翻译
联系
表示
转化
★
研究方法
研究内容
数形结合思想
类比思想
二、课时内容及其解析
二、课时内容及其解析
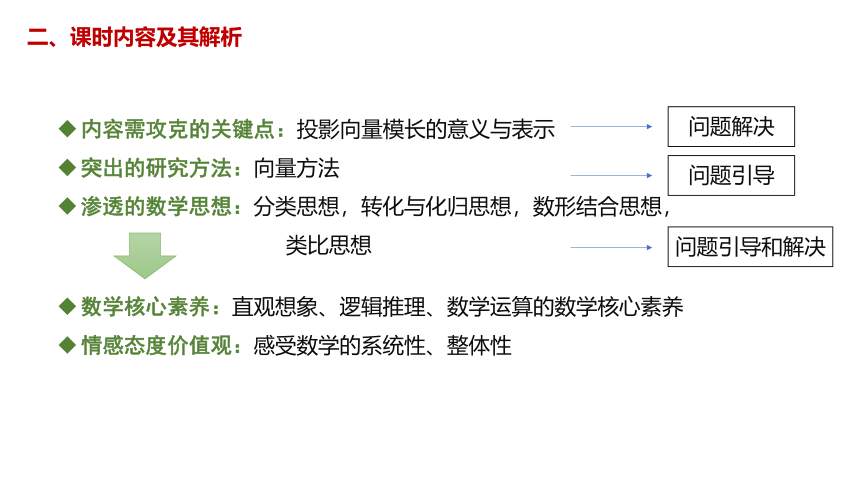
数学核心素养:直观想象、逻辑推理、数学运算的数学核心素养
情感态度价值观:感受数学的系统性、整体性
内容需攻克的关键点:投影向量模长的意义与表示
突出的研究方法:向量方法
渗透的数学思想:分类思想,转化与化归思想,数形结合思想,
类比思想
问题解决
问题引导
问题引导和解决
(二)教学目标
能利用投影向量得到点到直线、点到平面的距离公式,结合一些具体的距离问题的解决,归纳用空间向量解决立体几何问题的“三步曲”,渗透分类思想、转化与化归思想、数形结合思想。
(四)教学重点与难点
重点:利用投影向量推导点到直线的距离公式和点到平面的距离公式
难点:利用投影向量统一研究空间距离问题
二、课时内容及其解析
(三)育人目标
帮助学生归纳用空间向量解决立体几何问题的“三步曲”;
进一步体会向量及其运算在解决立体几何问题中的作用和“普适性”;
培养学生直观想象、数学运算和逻辑推理等素养.
已有的知识和能力:对距离有一定的认识,但缺乏整体性、系统性.会用空间向量及其运算、空间向量基本定理等解决了一些简单立体几何中的问题,但对向量法体会不深,对“三步曲”不够熟练。
即将要学习的知识:进一步用向量法解决距离等向量问题,归纳出向量解决立体几何问题的“三步曲”,系统运用向量法解决综合性问题。
可能存在的问题:对“建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题”缺乏经验和体会
三、教学问题诊断分析
三、教学过程分析
问题1 立体几何中有哪些距离问题?
追问:你能否对这些距离问题分分类?并说出你的分类依据
【设计意图】在分类过程中,对“距离”核心概念进行直观感知,利用转化思想,明确基本问题为点到直线的距离和点到平面的距离
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
追问3:借助图像,点P到直线l的距离如何求解?
表示
运算
翻译
设计意图:利用投影向量得到点到直线的距离,并通过问题链,引导学生利用向量方法解决立体几何问题。
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素与点P、距离之间能建立起怎样的联系?
P
l
直线几何要素:一点A一方向向量u(1.4.1)
u
A
Q
已知:A,P, u
未知:|PQ|
联系:构造直角三角形,利用勾股定理,所以转化为求解投影向量:|AQ|
a
表示
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
表示
P
l
u
A
Q
a
运算
AQ=|a|cosθ u
|AQ|=||a|cosθ u|= |=||a||u|cosθ |=| a u |
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
追问3:借助图像,点P到直线l的距离如何求解?
表示
运算
翻译
P
l
u
A
Q
a
三、教学过程分析
问题3 如何用向量方法求两平行线之间的距离?
设计意图:利用转化与化归思想,利用两平行线间的距离处处相等,化未知为已知,转化为点到直线的距离问题求解上
l1
l2
u
A
P
Q
a
三、教学过程分析
问题5 P 是平面 α外的一点,如何求点P到平面 α的距离?你认为应该如何研究?
P
α
设计意图:利用类比思想,类比点到直线的距离探究,先让学生明确具体研究思路:
①分析平面构成要素,用向量表示几何要素,即一点一法向量,
②建立联系,构造距离;
③转化为向量问题,即求解投影向量的模长
④进行向量运算和求解
三、教学过程分析
问题4 如果求平行与平面的直线l到平面的距离呢 两个平行平面之间的距离呢?
设计意图:利用转化与化归思想,化未知为已知,转化为点到平面的距离问题求解上
三、教学过程分析
例1:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)直线FC到平面AEC1的距离.
三、教学过程分析
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论。
问题6 结合例1,回顾用空间向量解决距离问题的过程,你能总结用向量法解决立体几何问题的基本步骤吗
向量法解决立体几何问题的“三步曲”
小结 本节课研究的主要内容有哪些?本节课我们采用的研究方法是什么?
三、教学过程分析
《用空间向量研究距离、夹角问题》说课
一、整体单元教学分析
主线:几何与代数
主题:立体几何与空间向量
单元:空间向量理论
必修课程:平面向量、立体几何初步
单元:空间向量应用
基点:用代数方法解决几何问题
空间向量及其概念
空间向量的运算
空间向量基本定理
空间向量的坐标表示及运算
位置关系
度量问题
平行
垂直
距离
夹角
直线方程:点到直线的距离
★向量方法
几何要素的向量表示
点、线、面
核心素养:
直观想象
逻辑推理
数学运算
二、课时内容及其解析
(一)教学内容
点到直线、点到平面、相互平行的直线、直线到平面(直线与平面平行)相互平行的平面的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两个平行平面间的距离
用垂直刻画
直观感受、
分类思想
点到平面的距离
两平行直线间的距离
直线到平面的距离
两个平行平面间的距离
点到直线的距离
两点间的距离
转化与化归思想
分类思想
向量的模长
★投影向量的模长
向量方法
①表示
②运算
③翻译
联系
表示
转化
★
研究方法
研究内容
数形结合思想
类比思想
二、课时内容及其解析
二、课时内容及其解析
数学核心素养:直观想象、逻辑推理、数学运算的数学核心素养
情感态度价值观:感受数学的系统性、整体性
内容需攻克的关键点:投影向量模长的意义与表示
突出的研究方法:向量方法
渗透的数学思想:分类思想,转化与化归思想,数形结合思想,
类比思想
问题解决
问题引导
问题引导和解决
(二)教学目标
能利用投影向量得到点到直线、点到平面的距离公式,结合一些具体的距离问题的解决,归纳用空间向量解决立体几何问题的“三步曲”,渗透分类思想、转化与化归思想、数形结合思想。
(四)教学重点与难点
重点:利用投影向量推导点到直线的距离公式和点到平面的距离公式
难点:利用投影向量统一研究空间距离问题
二、课时内容及其解析
(三)育人目标
帮助学生归纳用空间向量解决立体几何问题的“三步曲”;
进一步体会向量及其运算在解决立体几何问题中的作用和“普适性”;
培养学生直观想象、数学运算和逻辑推理等素养.
已有的知识和能力:对距离有一定的认识,但缺乏整体性、系统性.会用空间向量及其运算、空间向量基本定理等解决了一些简单立体几何中的问题,但对向量法体会不深,对“三步曲”不够熟练。
即将要学习的知识:进一步用向量法解决距离等向量问题,归纳出向量解决立体几何问题的“三步曲”,系统运用向量法解决综合性问题。
可能存在的问题:对“建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题”缺乏经验和体会
三、教学问题诊断分析
三、教学过程分析
问题1 立体几何中有哪些距离问题?
追问:你能否对这些距离问题分分类?并说出你的分类依据
【设计意图】在分类过程中,对“距离”核心概念进行直观感知,利用转化思想,明确基本问题为点到直线的距离和点到平面的距离
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
追问3:借助图像,点P到直线l的距离如何求解?
表示
运算
翻译
设计意图:利用投影向量得到点到直线的距离,并通过问题链,引导学生利用向量方法解决立体几何问题。
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素与点P、距离之间能建立起怎样的联系?
P
l
直线几何要素:一点A一方向向量u(1.4.1)
u
A
Q
已知:A,P, u
未知:|PQ|
联系:构造直角三角形,利用勾股定理,所以转化为求解投影向量:|AQ|
a
表示
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
表示
P
l
u
A
Q
a
运算
AQ=|a|cosθ u
|AQ|=||a|cosθ u|= |=||a||u|cosθ |=| a u |
三、教学过程分析
问题2 P 是直线 l 外的一点,如何求出点P 到 l 的距离 ?
追问1:直线有哪些几何要素构成?这些要素和点P之间能建
立起怎样的联系?
追问2:投影向量AQ的模长该如何表示?
追问3:借助图像,点P到直线l的距离如何求解?
表示
运算
翻译
P
l
u
A
Q
a
三、教学过程分析
问题3 如何用向量方法求两平行线之间的距离?
设计意图:利用转化与化归思想,利用两平行线间的距离处处相等,化未知为已知,转化为点到直线的距离问题求解上
l1
l2
u
A
P
Q
a
三、教学过程分析
问题5 P 是平面 α外的一点,如何求点P到平面 α的距离?你认为应该如何研究?
P
α
设计意图:利用类比思想,类比点到直线的距离探究,先让学生明确具体研究思路:
①分析平面构成要素,用向量表示几何要素,即一点一法向量,
②建立联系,构造距离;
③转化为向量问题,即求解投影向量的模长
④进行向量运算和求解
三、教学过程分析
问题4 如果求平行与平面的直线l到平面的距离呢 两个平行平面之间的距离呢?
设计意图:利用转化与化归思想,化未知为已知,转化为点到平面的距离问题求解上
三、教学过程分析
例1:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)直线FC到平面AEC1的距离.
三、教学过程分析
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论。
问题6 结合例1,回顾用空间向量解决距离问题的过程,你能总结用向量法解决立体几何问题的基本步骤吗
向量法解决立体几何问题的“三步曲”
小结 本节课研究的主要内容有哪些?本节课我们采用的研究方法是什么?
三、教学过程分析
