人教A版(2019)选择性必修一 1.1 空间向量及其运算 课件(共16张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修一 1.1 空间向量及其运算 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 22:49:15 | ||
图片预览






文档简介
(共16张PPT)
第一章空间向量与立体几何
1.1空间向量及其运算(第一课时)
1.向量的概念:既有大小,又有方向的量叫作向量.
3.向量的模:向量的大小。
4.零向量:长度为0的向量,方向是任意的。
5.单位向量:长度为1的向量,它们大小相等,但是方向不一定相同.
知识回顾
2.向量的表示方法:用字母来表示,或用表示向量的有向线段的起点和终点字母表示.
6.相等向量:长度相等且方向相同的向量叫做相等向量.
7.共线向量: 方向相同或相反的非零向量叫做平行向量.平行向量也叫做共线向量.
通过“平面向量及其应用”的学习,我们知道,平面内的点、直线可以通过平面向量及其运算来表示,它们之间的平行、垂直、夹角、距离等关系可以通过平面向量运算而得到,从而有关平面图形的问题可以利用平面向量的方法解决.能否把平面向量推广到空间向量,从而利用空间向量表示空间中点、直线、平面等基本元素,通过空间向量运算解决立体几何问题。
在本章学习中,我们要注意利用类比的方法理解空间向量的概念、运算、基本定理及其坐标表示,在此过程中体会平面向量与空间向量的共性和差异;在运用向量的方法研究空间基本图形的位置关系和度量关系的过程中,体会向量方法与综合几何方法的共性和差异;通过用向量方法解决数学问题和实际问题,感悟向量在研究几何问题中的作用。
空间向量的概念
1.定义:在空间,具有___________和___________的量叫做空间向量.2.长度或模:空间向量的___________.3.表示方法:(1)几何表示法:空间向量用___________表示;(2)字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,也可记作___________,其模记为_______________.
几类特殊的空间向量
名称 定义及表示
零向量 长度为0的向量叫做零向量,记为0
单位向量 长度为1的向量称为单位向量
相反向量 与向量a长度相等而方向相反的向量,称为a的相反向量,记为-a
共线向量(平行向量) 如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.规定:对于任意向量a,都有 0∥a
相等向量 方向相同且模相等的向量称为相等向量
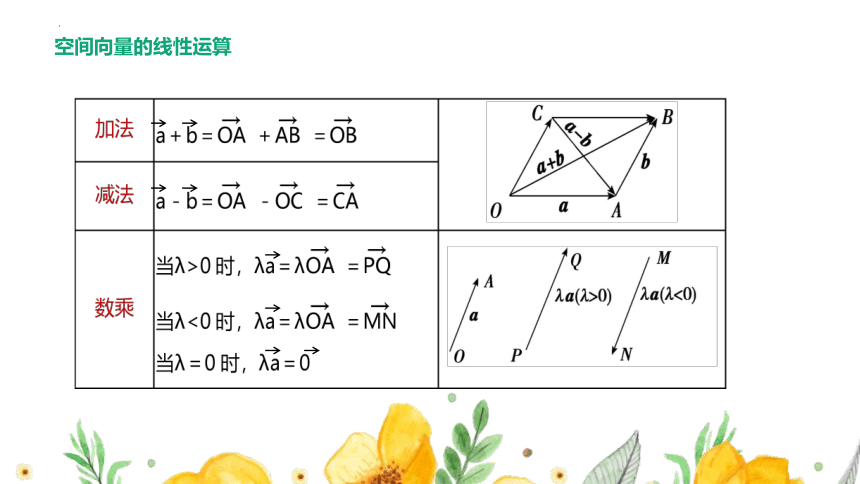
空间向量的线性运算
空间向量的线性运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律: ;
结合律: ;
分配律:(λ+μ)=+μ ,(a+b)=+.
共线向量与共面向量
课堂总结
1.空间向量的基本概念;
2.空间向量的基本运算;
3.共面向量定理。
第一章空间向量与立体几何
1.1空间向量及其运算(第一课时)
1.向量的概念:既有大小,又有方向的量叫作向量.
3.向量的模:向量的大小。
4.零向量:长度为0的向量,方向是任意的。
5.单位向量:长度为1的向量,它们大小相等,但是方向不一定相同.
知识回顾
2.向量的表示方法:用字母来表示,或用表示向量的有向线段的起点和终点字母表示.
6.相等向量:长度相等且方向相同的向量叫做相等向量.
7.共线向量: 方向相同或相反的非零向量叫做平行向量.平行向量也叫做共线向量.
通过“平面向量及其应用”的学习,我们知道,平面内的点、直线可以通过平面向量及其运算来表示,它们之间的平行、垂直、夹角、距离等关系可以通过平面向量运算而得到,从而有关平面图形的问题可以利用平面向量的方法解决.能否把平面向量推广到空间向量,从而利用空间向量表示空间中点、直线、平面等基本元素,通过空间向量运算解决立体几何问题。
在本章学习中,我们要注意利用类比的方法理解空间向量的概念、运算、基本定理及其坐标表示,在此过程中体会平面向量与空间向量的共性和差异;在运用向量的方法研究空间基本图形的位置关系和度量关系的过程中,体会向量方法与综合几何方法的共性和差异;通过用向量方法解决数学问题和实际问题,感悟向量在研究几何问题中的作用。
空间向量的概念
1.定义:在空间,具有___________和___________的量叫做空间向量.2.长度或模:空间向量的___________.3.表示方法:(1)几何表示法:空间向量用___________表示;(2)字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,也可记作___________,其模记为_______________.
几类特殊的空间向量
名称 定义及表示
零向量 长度为0的向量叫做零向量,记为0
单位向量 长度为1的向量称为单位向量
相反向量 与向量a长度相等而方向相反的向量,称为a的相反向量,记为-a
共线向量(平行向量) 如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.规定:对于任意向量a,都有 0∥a
相等向量 方向相同且模相等的向量称为相等向量
空间向量的线性运算
空间向量的线性运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律: ;
结合律: ;
分配律:(λ+μ)=+μ ,(a+b)=+.
共线向量与共面向量
课堂总结
1.空间向量的基本概念;
2.空间向量的基本运算;
3.共面向量定理。
