9.3.1不等式组的应用 课件(共23张PPT)
文档属性
| 名称 | 9.3.1不等式组的应用 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 07:22:30 | ||
图片预览








文档简介
(共23张PPT)
第九章
不等式与不等式组
9.3.1不等式组的应用
教学目标/Teaching aims
1
1.理解列不等式解决实际问题的思想方法,找出题中的数量关系.
2
2.寻找实际问题中的不等关系,建立数学模型.
复习回顾
思考:
一元一次方程的解题步骤:
1.审题:找等量关系;
2.根据题意设未知量;
3.根据等量关系列方程;
4.解方程,并检验;
5.作答。
情景导入
x+3<0
一元一次不等式组的概念
新知探究
用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
(1)若设用x min将污水抽完,你能列出满足条件的不等式吗?
30x>1200
30x<1500
类似方程组,把这两个不等式合起来,组成一个一元一次不等式组。
①组成一元一次不等式组的每个不等式都必须是一元一次不等式。
②这几个一元一次不等式必须是关于同一个未知数的不等式。
③这里的几个可以是两个或者两个以上。
一元一次不等式组的解集
新知探究
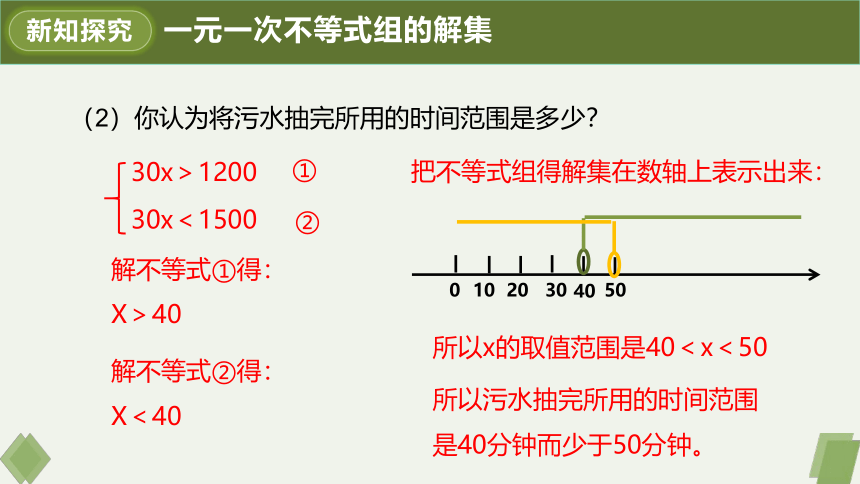
(2)你认为将污水抽完所用的时间范围是多少?
30x>1200
30x<1500
①
②
解不等式①得:
X>40
解不等式②得:
X<40
把不等式组得解集在数轴上表示出来:
0
10
20
30
40
50
所以x的取值范围是40<x<50
所以污水抽完所用的时间范围是40分钟而少于50分钟。
一元一次不等式组的解集
新知探究
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集,解不等式组就是求它的解集。
(1)公共部分指在数轴上被几个不等式解集所在区域都覆盖住的部分。
(2)写不等式组得解集应注意分界点和方向。简记为:大于向右画,小于向左画,包含用实心圆点,不包含用空心圆点,。解集中包含≥或者≤时,界点处用实心圆,解集中包含>或<,界点处用空心圆。
巩固练习
1.下列各式不是一元一次不等式组的是( )
D
巩固练习
2.下列不等式组中,解集是2<x<3的不等式组是( )
A. B.
C. D.
C
一元一次不等式组的应用
新知探究
一元一次不等式组的应用
新知探究
一元一次不等式组的应用
新知探究
巩固练习
巩固练习
巩固练习
课堂练习
1.在数轴上从左至右的三个数为a,1+a,-a,则a的取值范围是( )
D
课堂练习
2.在平面直角坐标系内,P(2x-6,x-5)在第四象限,则x的取值范围为( )
A.3<x<5 B.-3<x<5 C.-5<x<3 D.-5<x<-3
A
课堂练习
B
课堂练习
A
课堂练习
课堂练习
课堂总结
一元一次不等式组应用题的步骤
(1)审:认真审题,分清已知量、未知量及其关系,找出题中不等关系要抓住题中的关键字眼,如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等;
(2)设:设出适当的未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)答:写出答案,并检验是否符合题意.
9.3.1不等式组的应用
谢谢观看
不等式与不等式组
第九章
不等式与不等式组
9.3.1不等式组的应用
教学目标/Teaching aims
1
1.理解列不等式解决实际问题的思想方法,找出题中的数量关系.
2
2.寻找实际问题中的不等关系,建立数学模型.
复习回顾
思考:
一元一次方程的解题步骤:
1.审题:找等量关系;
2.根据题意设未知量;
3.根据等量关系列方程;
4.解方程,并检验;
5.作答。
情景导入
x+3<0
一元一次不等式组的概念
新知探究
用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
(1)若设用x min将污水抽完,你能列出满足条件的不等式吗?
30x>1200
30x<1500
类似方程组,把这两个不等式合起来,组成一个一元一次不等式组。
①组成一元一次不等式组的每个不等式都必须是一元一次不等式。
②这几个一元一次不等式必须是关于同一个未知数的不等式。
③这里的几个可以是两个或者两个以上。
一元一次不等式组的解集
新知探究
(2)你认为将污水抽完所用的时间范围是多少?
30x>1200
30x<1500
①
②
解不等式①得:
X>40
解不等式②得:
X<40
把不等式组得解集在数轴上表示出来:
0
10
20
30
40
50
所以x的取值范围是40<x<50
所以污水抽完所用的时间范围是40分钟而少于50分钟。
一元一次不等式组的解集
新知探究
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集,解不等式组就是求它的解集。
(1)公共部分指在数轴上被几个不等式解集所在区域都覆盖住的部分。
(2)写不等式组得解集应注意分界点和方向。简记为:大于向右画,小于向左画,包含用实心圆点,不包含用空心圆点,。解集中包含≥或者≤时,界点处用实心圆,解集中包含>或<,界点处用空心圆。
巩固练习
1.下列各式不是一元一次不等式组的是( )
D
巩固练习
2.下列不等式组中,解集是2<x<3的不等式组是( )
A. B.
C. D.
C
一元一次不等式组的应用
新知探究
一元一次不等式组的应用
新知探究
一元一次不等式组的应用
新知探究
巩固练习
巩固练习
巩固练习
课堂练习
1.在数轴上从左至右的三个数为a,1+a,-a,则a的取值范围是( )
D
课堂练习
2.在平面直角坐标系内,P(2x-6,x-5)在第四象限,则x的取值范围为( )
A.3<x<5 B.-3<x<5 C.-5<x<3 D.-5<x<-3
A
课堂练习
B
课堂练习
A
课堂练习
课堂练习
课堂总结
一元一次不等式组应用题的步骤
(1)审:认真审题,分清已知量、未知量及其关系,找出题中不等关系要抓住题中的关键字眼,如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等;
(2)设:设出适当的未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)答:写出答案,并检验是否符合题意.
9.3.1不等式组的应用
谢谢观看
不等式与不等式组
