2022-2023学年鲁教版初中数学六年级下学期经典精练之数据的收集、整理与描述(含解析)
文档属性
| 名称 | 2022-2023学年鲁教版初中数学六年级下学期经典精练之数据的收集、整理与描述(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 482.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 00:00:00 | ||
图片预览



文档简介
2022-2023学年初中数学六年级下学期经典精练之数据的收集、整理与描述
一.选择题(共10小题)
1.(2022秋 驻马店期末)下列说法中,正确的是( )
A.了解你们班同学周末时间如何按需要进行抽样检查
B.了解全国中学生的节水意识需要进行普查
C.神舟飞船发射前需要对零部件进行抽样检查
D.了解某种节能灯的使用寿命适合抽样调查
2.(2021秋 仁寿县期末)新型冠状病毒肺炎(CoronaVriusDisease2019,COVID﹣19),简称“新冠肺炎”,世界卫生组织命名为“2019冠状病毒病”,英文单词CoronaVriusDisease中字母r出现的频数是( )
A.2 B.11.1% C.18 D.
3.(2022秋 新都区期末)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
4.(2022秋 太原期末)一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
5.(2022秋 胶州市期末)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.组距为10
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
6.(2022秋 海淀区校级期中)小明同学统计了某学校八年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示.下面有四个推断:
①小明此次一共调查了100位同学;
②每天阅读图书时间不足15分钟的同学人数多于45﹣60分钟的人数;
③每天阅读图书时间在15﹣30分钟的人数最多;
④每天阅读图书时间超过30分钟的同学人数是调查总人数的20%.
根据图中信息,上述说法中正确的是( )
A.①③ B.①④ C.②③ D.②④
7.(2022秋 长沙期末)长沙网红打卡点铜官窑古镇为迎接“五一”假期新增了骑马、威亚、卡丁车、低空飞行4项互动体验项目,并对部分游客所喜欢的项目进行调查问卷(每个游客均只选择一个喜欢的项目),统计如图,其中喜欢威亚的有80人,则本次调查的游客有( )人.
A.120 B.160 C.300 D.400
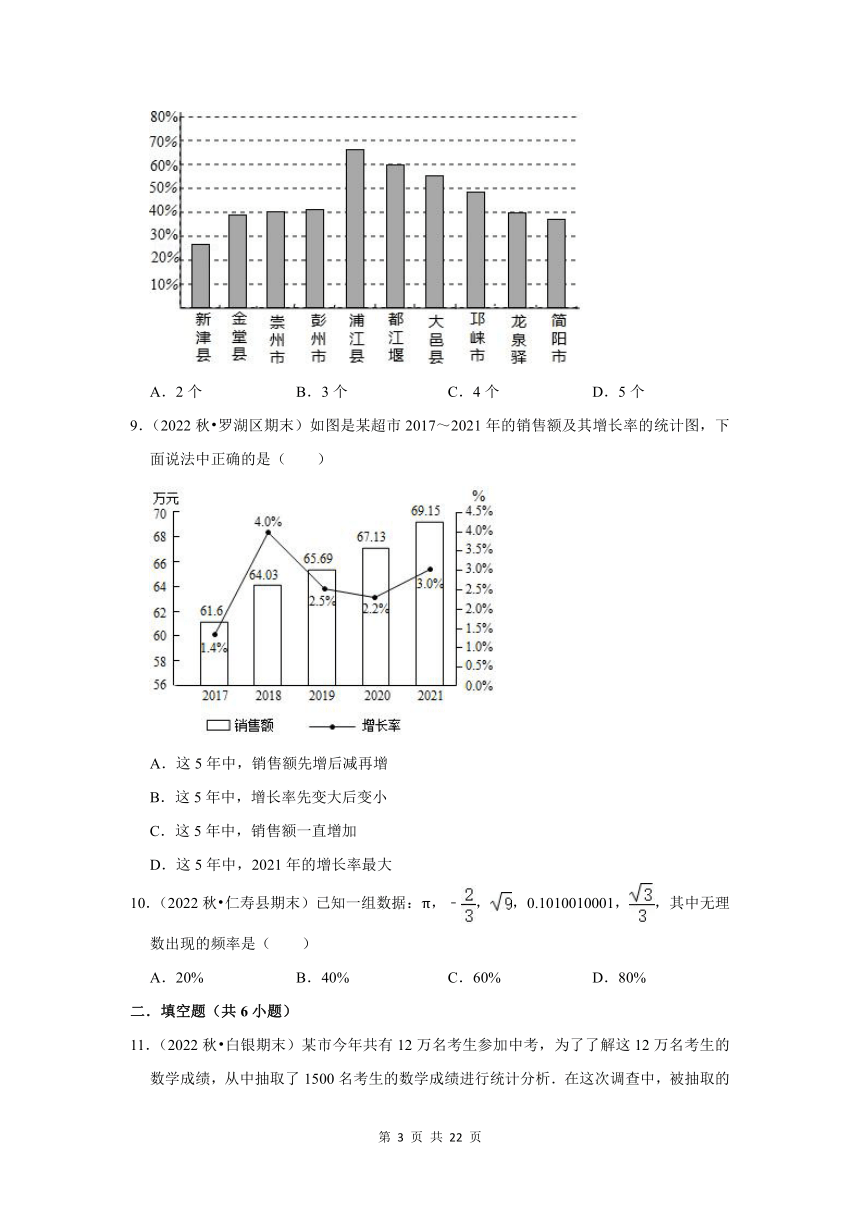
8.(2022秋 成华区期末)绿水青山就是金山银山.如图为成都部分区县森林覆盖率统计图,其中森林覆盖率高于50%的区县有( )
A.2个 B.3个 C.4个 D.5个
9.(2022秋 罗湖区期末)如图是某超市2017~2021年的销售额及其增长率的统计图,下面说法中正确的是( )
A.这5年中,销售额先增后减再增
B.这5年中,增长率先变大后变小
C.这5年中,销售额一直增加
D.这5年中,2021年的增长率最大
10.(2022秋 仁寿县期末)已知一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率是( )
A.20% B.40% C.60% D.80%
二.填空题(共6小题)
11.(2022秋 白银期末)某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是 .(填“总体”,“样本”或“个体”)
12.(2022秋 新都区期末)成都市于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾,可回收物,其他垃圾和有害垃圾四类.通过调查某小区四类垃圾的比例,整理制作出如图扇形图,若某个月该小区产生各类垃圾共80吨,其中可回收物有 吨.
13.(2022秋 沈丘县期末)一组数据4,﹣4,,4,,4,﹣4,4中,出现次数最多的数是4,其频率是 .
14.(2022秋 锦州期末)下列是根据我国历次人口普查数据,绘制的全国人口年平均增长率的折线图,根据图中提供的信息,可以判断我国人口年平均增长率的变化趋势是逐渐 .(填“下降”或“上升”)
15.(2022秋 南县期末)为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查,整理样本数据,得到如表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区15000名初中学生视力不低于4.8的人数是 .
16.(2022秋 市北区期末)一个不透明袋子中装有30个小球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中随机摸出1个球,记下颜色后放回搅匀,并重复该过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.3600 0.3100 0.3250 0.3340 0.3325 0.3335
该学习小组发现,摸到红球的频率在一个常数附近波动,由此估算出红球个数是 个.
三.解答题(共4小题)
17.(2022 邓州市一模)某校为了解学生对我国社会主义现代化建设中“两个一百年”奋斗目标的知晓情况,对全校学生进行了相关知识测试(满分为100分),并从七、八年级各随机抽取了10名同学的成绩,收集数据为:
七年级:90,95,95,80,90,80,85,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90;
整理数据:
分数人数年级 80 85 90 95 100
七年级 2 2 3 2 1
八年级 1 2 a 2 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 90 90 c 30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c的值;
(2)通过数据分析你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次测试成绩不低于90分的为“优秀“,估计这两个年级共有多少名学生达到“优秀”.
18.(2023春 温州期末)为丰富学生的课余生活,培养学生的爱好,陶冶学生的情操,某校开展学生拓展课,为了解学生各社团活动的参与人数,该校对参与社团活动的学生进行了抽样调查,制作出如下的统计图根据该统计图,完成以下问题:
(1)这次共调查了 名学生;
(2)请把统计图1补充完整;
(3)已知该校七年级共有680名学生参加社团活动,请根据样本估算该校七年级学生参加艺术类社团的人数
19.(2022 温州校级模拟)在推进城乡生活垃圾分类的行动中,社区从A,B两个小区各随机选择50位居民进行问卷调查,并得到他们的成绩,将成绩a<60定为“不了解”,60<a≤80为“比较了解”,80<a≤100为“非常了解“,并绘制了如图的统计图:
(每一组不包含前一个边界值,包含后一个边界值)
已知A小区共有常住居民500人,B小区共有常住居民400人,
(1)请估计整个B小区达到“非常了解”的居民人数.
(2)将“比较了解”和“非常了解”的人数作为普及到位的居民,请估计整个A小区普及到位的居民人数.
(3)你认为哪个小区垃圾分类的普及工作更出色?请通过计算并用合适的数据来说明.
20.(2023春 敦化市期末)某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐;B.去影院看电影;C.到公园游玩;D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成统计图.根据统计图提供的信息,解答下列问题:
(1)请直接写出n的值; ;
(2)四种方式中最受学生喜欢的方式为 (用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 ;
(3)根据统计结果,估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
2022-2023学年初中数学六年级下学期经典精练之数据的收集、整理与描述
一.选择题(共10小题)
1.(2022秋 驻马店期末)下列说法中,正确的是( )
A.了解你们班同学周末时间如何按需要进行抽样检查
B.了解全国中学生的节水意识需要进行普查
C.神舟飞船发射前需要对零部件进行抽样检查
D.了解某种节能灯的使用寿命适合抽样调查
【考点】抽样调查的可靠性.
【专题】数据的收集与整理;数据分析观念.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【解答】解:A、了解你们班同学周末时间是如何安排的,适合普查,故不符合题意;
B、了解全国中学生的节水意识,工作量较大,且没有必要,适合抽样调查,故不符合题意;
C、神舟飞船发射前需要对零部件进行全面调查,故不符合题意;
D、了解某种节能灯的使用寿命适合抽样调查,故符合题意.
故选:D.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.(2021秋 仁寿县期末)新型冠状病毒肺炎(CoronaVriusDisease2019,COVID﹣19),简称“新冠肺炎”,世界卫生组织命名为“2019冠状病毒病”,英文单词CoronaVriusDisease中字母r出现的频数是( )
A.2 B.11.1% C.18 D.
【考点】频数与频率.
【专题】数据的收集与整理;数据分析观念.
【分析】根据CoronaVriusDisease中共有18个字母,其中r出现2次可得答案.
【解答】解:CoronaVriusDisease中共有18个字母,其中r出现2次,
∴频数是2,
故选:A.
【点评】本题考查频数的定义,熟练掌握频数的定义是解题关键.
3.(2022秋 新都区期末)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
【考点】频数(率)分布直方图;频数(率)分布折线图;统计图的选择.
【专题】统计的应用;数据分析观念.
【分析】根据三种统计图的特点判断即可.
【解答】解:最宜反映人体体温变化的是:折线统计图,
故选:A.
【点评】本题考查了统计图的选择,频数分布直方图,频数分布折线图,熟练掌握三种统计图的特点是解题的关键.
4.(2022秋 太原期末)一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
【考点】用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【分析】估计利用频率估计概率可估计摸到红球的概率为0.7,然后根据概率公式计算这个口袋中红球的数量.
【解答】解:因为共摸了200次球,发现有140次摸到红球,
所以估计摸到红球的概率为0.7,
所以估计这个口袋中红球的数量为10×0.7=7(个).
故选:D.
【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
5.(2022秋 胶州市期末)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.组距为10
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
【考点】频数(率)分布表;频数(率)分布直方图.
【专题】数据的收集与整理;统计的应用;数据分析观念;运算能力.
【分析】根据条形统计图所表示的意义逐项进行判断即可.
【解答】解:从条形统计图可知,
得分在70~80分的人数最多,是14人,因此选项A不符合题意;
组距为60﹣50=70﹣60=80﹣70=90﹣80=10,因此选项B不符合题意;
人数最少的是“90﹣100”分数段的,是2人,因此选项C不符合题意;
得分及格(≥60)的有12+14+8+2=36(人),因此选项D符合题意;
故选:D.
【点评】本题考查频数分布直方图,理解条形统计图所表示数据的特征是正确判断的前提.
6.(2022秋 海淀区校级期中)小明同学统计了某学校八年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示.下面有四个推断:
①小明此次一共调查了100位同学;
②每天阅读图书时间不足15分钟的同学人数多于45﹣60分钟的人数;
③每天阅读图书时间在15﹣30分钟的人数最多;
④每天阅读图书时间超过30分钟的同学人数是调查总人数的20%.
根据图中信息,上述说法中正确的是( )
A.①③ B.①④ C.②③ D.②④
【考点】频数(率)分布直方图.
【专题】数据的收集与整理;统计的应用;数据分析观念.
【分析】根据频数分布直方图中的数据,可以判断各个小题中的说法是否正确,从而可以解答本题.
【解答】解:由直方图可得,
小明此次一共调查了10+60+20+10=100名同学,故①正确;
每天阅读图书时间不足15分钟的同学人数和45﹣60分钟的人数一样多,故②错误;
每天阅读图书时间在15﹣30分钟的人数最多,故③正确;
每天阅读图书时间超过30分钟的同学人数是调查总人数的:(20+10)÷100×100%=30%,故④错误;
故选:A.
【点评】本题考查频数分布直方图,利用数形结合的思想解答是解答本题的关键.
7.(2022秋 长沙期末)长沙网红打卡点铜官窑古镇为迎接“五一”假期新增了骑马、威亚、卡丁车、低空飞行4项互动体验项目,并对部分游客所喜欢的项目进行调查问卷(每个游客均只选择一个喜欢的项目),统计如图,其中喜欢威亚的有80人,则本次调查的游客有( )人.
A.120 B.160 C.300 D.400
【考点】扇形统计图.
【专题】统计的应用;运算能力.
【分析】根据喜欢威亚的人数和所占的百分比即可得出答案.
【解答】解:本次调查的游客人数有;80÷20%=400(人).
故选:D.
【点评】本题考查的是扇形统计图.读懂统计图,从扇形统计图中得到相关的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.
8.(2022秋 成华区期末)绿水青山就是金山银山.如图为成都部分区县森林覆盖率统计图,其中森林覆盖率高于50%的区县有( )
A.2个 B.3个 C.4个 D.5个
【考点】条形统计图.
【专题】数据的收集与整理;数据分析观念.
【分析】由条形图中森林覆盖率高于50%的城市有浦江县、都江堰、大邑县可得答案.
【解答】解:由条形图中森林覆盖率高于50%的城市有浦江县、都江堰、大邑县,
故选:B.
【点评】本题主要考查条形统计图,解题的关键是掌握条形图的特点:从条形图可以很容易看出数据的大小,便于比较.
9.(2022秋 罗湖区期末)如图是某超市2017~2021年的销售额及其增长率的统计图,下面说法中正确的是( )
A.这5年中,销售额先增后减再增
B.这5年中,增长率先变大后变小
C.这5年中,销售额一直增加
D.这5年中,2021年的增长率最大
【考点】折线统计图.
【专题】统计的应用;应用意识.
【分析】根据折线统计图的意义解答.
【解答】解:根据折线统计图可知,这5年中,销售额在增大,增长率先增后减再增,2018年的增长率最大.
故选:C.
【点评】本题考查了折线统计图,要分析清楚折线统计图的意义.
10.(2022秋 仁寿县期末)已知一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率是( )
A.20% B.40% C.60% D.80%
【考点】算术平方根;无理数;频数与频率.
【专题】统计的应用.
【分析】根据频率的定义解决问题即可.
【解答】解:一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率==40%,
故选:B.
【点评】本题考查频数与频率,无理数,有理数等知识,解题的关键是理解频率的定义,属于中考常考题型.
二.填空题(共6小题)
11.(2022秋 白银期末)某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是 样本 .(填“总体”,“样本”或“个体”)
【考点】总体、个体、样本、样本容量.
【专题】数据的收集与整理;数据分析观念.
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.
【解答】解:某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是样本.
故答案为:样本.
【点评】本题考查的是确定总体、个体和样本.解此类题需要注意考察对象实际应是表示事物某一特征的数据,而非考查的事物.
12.(2022秋 新都区期末)成都市于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾,可回收物,其他垃圾和有害垃圾四类.通过调查某小区四类垃圾的比例,整理制作出如图扇形图,若某个月该小区产生各类垃圾共80吨,其中可回收物有 20.8 吨.
【考点】扇形统计图.
【专题】统计的应用;数据分析观念;运算能力.
【分析】由扇形统计图可知,“可回收垃圾”占垃圾总量的26%,求出80吨的26%即可.
【解答】解:由扇形统计图可知,“可回收垃圾”占垃圾总量的26%,
即80×26%=20.8(吨),
故答案为:20.8.
【点评】本题考查扇形统计图,理解扇形统计图中各个部分所占整体的百分比是解决问题的关键.
13.(2022秋 沈丘县期末)一组数据4,﹣4,,4,,4,﹣4,4中,出现次数最多的数是4,其频率是 0.5 .
【考点】频数与频率.
【专题】概率及其应用;数据分析观念.
【分析】用4出现的次数除以数据的个数即可.
【解答】解:4出现的频率是4÷8=0.5.
故答案为:0.5.
【点评】本题考查了频数与频率:频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
14.(2022秋 锦州期末)下列是根据我国历次人口普查数据,绘制的全国人口年平均增长率的折线图,根据图中提供的信息,可以判断我国人口年平均增长率的变化趋势是逐渐 下降 .(填“下降”或“上升”)
【考点】折线统计图.
【专题】数据的收集与整理;数据分析观念.
【分析】折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.
【解答】解:根据折线统计图可知,我国人口年平均增长率的变化趋势是逐渐下降.
故答案为:下降.
【点评】本题考查的是折线统计图.读懂统计图并从统计图中得到必要的信息是解决问题的关键.
15.(2022秋 南县期末)为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查,整理样本数据,得到如表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区15000名初中学生视力不低于4.8的人数是 9000人 .
【考点】用样本估计总体.
【专题】统计的应用;数据分析观念.
【分析】用总人数乘以样本中视力不低于4.8的人数所占比例即可.
【解答】解:估计该区15000名初中学生视力不低于4.8的人数是15000×=9000(人),
故答案为:9000人.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
16.(2022秋 市北区期末)一个不透明袋子中装有30个小球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中随机摸出1个球,记下颜色后放回搅匀,并重复该过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.3600 0.3100 0.3250 0.3340 0.3325 0.3335
该学习小组发现,摸到红球的频率在一个常数附近波动,由此估算出红球个数是 10 个.
【考点】用样本估计总体;频数与频率.
【专题】统计的应用;应用意识.
【分析】通过表格中数据,随着次数的增多,摸到白球的频率越稳定在0.3335左右,估计得出答案.
【解答】解:由题意摸到白球的频率在一个常数附近摆动,这个常数是0.3335,
由此估出红球有30×0.3335≈10(个).
故答案为:10.
【点评】本题考查频数与频率,解题的关键是掌握频率的定义,属于中考常考题型.
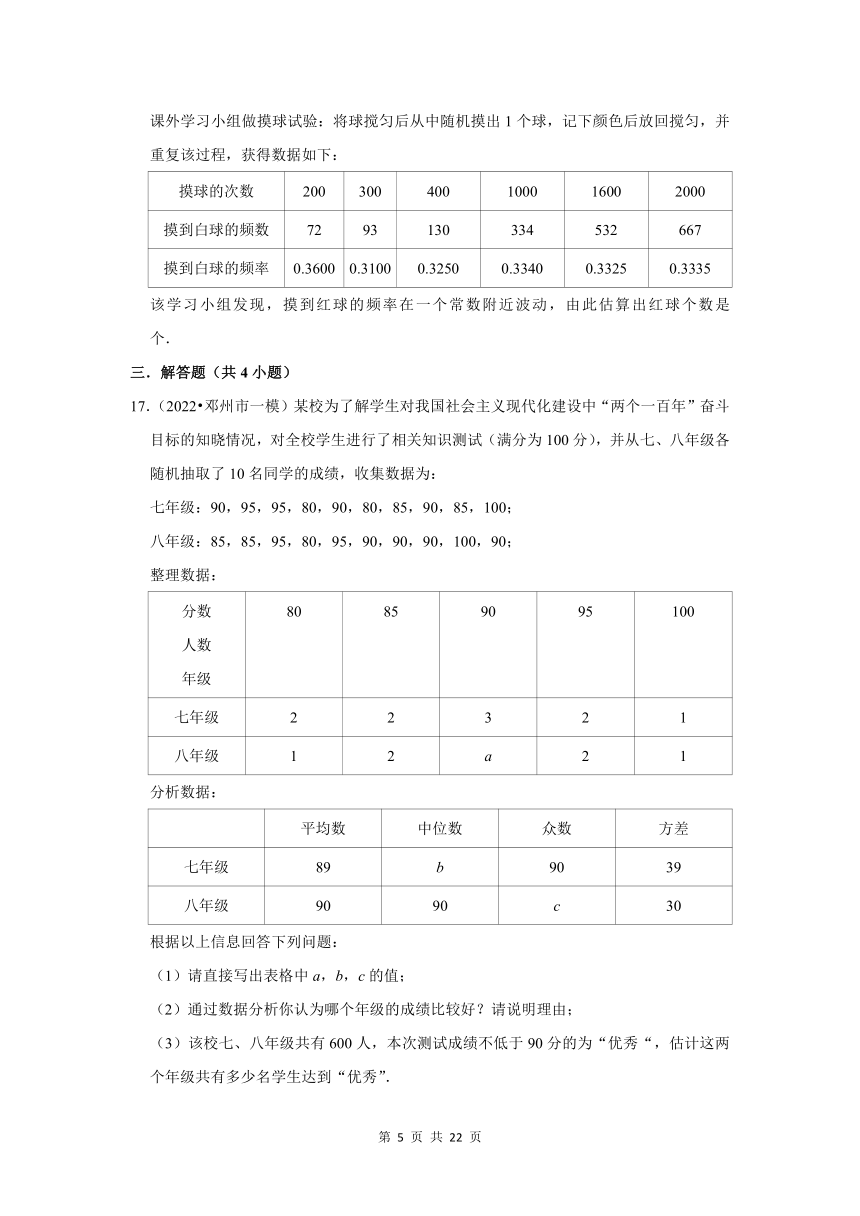
三.解答题(共4小题)
17.(2022 邓州市一模)某校为了解学生对我国社会主义现代化建设中“两个一百年”奋斗目标的知晓情况,对全校学生进行了相关知识测试(满分为100分),并从七、八年级各随机抽取了10名同学的成绩,收集数据为:
七年级:90,95,95,80,90,80,85,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90;
整理数据:
分数人数年级 80 85 90 95 100
七年级 2 2 3 2 1
八年级 1 2 a 2 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 90 90 c 30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c的值;
(2)通过数据分析你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次测试成绩不低于90分的为“优秀“,估计这两个年级共有多少名学生达到“优秀”.
【考点】用样本估计总体.
【专题】统计的应用;应用意识.
【分析】(1)根据八年级抽取的10名同学的成绩求出a的值,根据中位数和众数的概念求出b,c的值;
(2)比较七、八年级的平均数、中位数、众数以及方差的大小,即可得出答案;
(3)用600乘以样本中七、八年级测试成绩不低于90分所占的比例即可.
【解答】解:(1)由题意可得,a=4.
将七年级抽样成绩重新排列为:80,80,85,85,90,90,90,95,95,100,
位于中间位置的两个数都是90,所以中位数b==90,
90出现了3次,次数最多,所以众数c=90;
(2)八年级的成绩比较好.理由如下:
虽然七、八年级成绩的中位数与众数相同,但是八年级的成绩的平均数比七年级高,方差比七年级小,
所以八年级的成绩比较好;
(3)600×=390(人),
故估计这两个年级共有390名学生达到“优秀”.
【点评】本题考查中位数、众数、平均数、方差以及用样本估计总体,解答本题的关键是明确题意,掌握中位数、众数、平均数、方差的意义.
18.(2023春 温州期末)为丰富学生的课余生活,培养学生的爱好,陶冶学生的情操,某校开展学生拓展课,为了解学生各社团活动的参与人数,该校对参与社团活动的学生进行了抽样调查,制作出如下的统计图根据该统计图,完成以下问题:
(1)这次共调查了 80 名学生;
(2)请把统计图1补充完整;
(3)已知该校七年级共有680名学生参加社团活动,请根据样本估算该校七年级学生参加艺术类社团的人数
【考点】用样本估计总体.
【专题】统计的应用;运算能力.
【分析】(1)根据A社团的人数和所占的百分比即可得出答案;
(2)用总人数减去其他社团的人数,求出B社团的人数,从而补全统计图;
(3)用总人数乘以参加艺术类社团的人数所占的百分比即可.
【解答】解:(1)这次共调查的学生有:32÷40%=80(名).
故答案为:80;
(2)B社团的人数有:80﹣32﹣24﹣8=16(名),补全统计图如下:
(3)680×=136(名),
答:估算该校七年级学生参加艺术类社团的人数有136名.
【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
19.(2022 温州校级模拟)在推进城乡生活垃圾分类的行动中,社区从A,B两个小区各随机选择50位居民进行问卷调查,并得到他们的成绩,将成绩a<60定为“不了解”,60<a≤80为“比较了解”,80<a≤100为“非常了解“,并绘制了如图的统计图:
(每一组不包含前一个边界值,包含后一个边界值)
已知A小区共有常住居民500人,B小区共有常住居民400人,
(1)请估计整个B小区达到“非常了解”的居民人数.
(2)将“比较了解”和“非常了解”的人数作为普及到位的居民,请估计整个A小区普及到位的居民人数.
(3)你认为哪个小区垃圾分类的普及工作更出色?请通过计算并用合适的数据来说明.
【考点】调查收集数据的过程与方法;用样本估计总体.
【专题】数据的收集与整理;数据分析观念;运算能力.
【分析】(1)用整个B小区总人数乘以样本中“非常了解”的人数的百分比,即可估计整个B小区达到“非常了解”的居民人数;
(2)用整个A小区总人数乘以样本中“比较了解”和“非常了解”的人数的频率,即可估计整个A小区普及到位的居民人数;
(3)计算出两个小区样本“不了解”的人数的百分比,用样本估计总体
【解答】解:(1)估计整个B小区达到“非常了解”的居民人数有:400×24%=96(人);
(2)整个A小区普及到位的居民人数有:500×=250(人);
(3)因为整个A小区“不了解”的=50%,500×50%=250(人);
整个B小区“不了解”的44%,44%×400=176(人).
所以B小区垃圾分类的普及工作更出色.
【点评】本题考查了用样本估计总体,调查收集数据的过程与方法,解决本题的关键是掌握用样本估计总体.
20.(2023春 敦化市期末)某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐;B.去影院看电影;C.到公园游玩;D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成统计图.根据统计图提供的信息,解答下列问题:
(1)请直接写出n的值; 200 ;
(2)四种方式中最受学生喜欢的方式为 C (用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 35% ;
(3)根据统计结果,估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
【考点】全面调查与抽样调查;用样本估计总体.
【专题】统计的应用;运算能力.
【分析】(1)根据条形图,把A,B,C,D的人数加起来,即可解答;
(2)C的学生人数最多,即为四种方式中最受学生喜欢的方式;用C的人数÷总人数,即可得到百分比;
(3)用该校的总人数乘以喜欢C方式的学生比喜欢B方式的学生多占的百分比即可.
【解答】解:(1)n=30+40+70+60=200.
故答案为:200;
(2)∵C的学生人数最多,
∴四种方式中最受学生喜欢的方式为C,
×100%=35%,
故答案为:C,35%.
(3)1200×(﹣)=180(人),
答:估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数为180人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据
一.选择题(共10小题)
1.(2022秋 驻马店期末)下列说法中,正确的是( )
A.了解你们班同学周末时间如何按需要进行抽样检查
B.了解全国中学生的节水意识需要进行普查
C.神舟飞船发射前需要对零部件进行抽样检查
D.了解某种节能灯的使用寿命适合抽样调查
2.(2021秋 仁寿县期末)新型冠状病毒肺炎(CoronaVriusDisease2019,COVID﹣19),简称“新冠肺炎”,世界卫生组织命名为“2019冠状病毒病”,英文单词CoronaVriusDisease中字母r出现的频数是( )
A.2 B.11.1% C.18 D.
3.(2022秋 新都区期末)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
4.(2022秋 太原期末)一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
5.(2022秋 胶州市期末)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.组距为10
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
6.(2022秋 海淀区校级期中)小明同学统计了某学校八年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示.下面有四个推断:
①小明此次一共调查了100位同学;
②每天阅读图书时间不足15分钟的同学人数多于45﹣60分钟的人数;
③每天阅读图书时间在15﹣30分钟的人数最多;
④每天阅读图书时间超过30分钟的同学人数是调查总人数的20%.
根据图中信息,上述说法中正确的是( )
A.①③ B.①④ C.②③ D.②④
7.(2022秋 长沙期末)长沙网红打卡点铜官窑古镇为迎接“五一”假期新增了骑马、威亚、卡丁车、低空飞行4项互动体验项目,并对部分游客所喜欢的项目进行调查问卷(每个游客均只选择一个喜欢的项目),统计如图,其中喜欢威亚的有80人,则本次调查的游客有( )人.
A.120 B.160 C.300 D.400
8.(2022秋 成华区期末)绿水青山就是金山银山.如图为成都部分区县森林覆盖率统计图,其中森林覆盖率高于50%的区县有( )
A.2个 B.3个 C.4个 D.5个
9.(2022秋 罗湖区期末)如图是某超市2017~2021年的销售额及其增长率的统计图,下面说法中正确的是( )
A.这5年中,销售额先增后减再增
B.这5年中,增长率先变大后变小
C.这5年中,销售额一直增加
D.这5年中,2021年的增长率最大
10.(2022秋 仁寿县期末)已知一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率是( )
A.20% B.40% C.60% D.80%
二.填空题(共6小题)
11.(2022秋 白银期末)某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是 .(填“总体”,“样本”或“个体”)
12.(2022秋 新都区期末)成都市于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾,可回收物,其他垃圾和有害垃圾四类.通过调查某小区四类垃圾的比例,整理制作出如图扇形图,若某个月该小区产生各类垃圾共80吨,其中可回收物有 吨.
13.(2022秋 沈丘县期末)一组数据4,﹣4,,4,,4,﹣4,4中,出现次数最多的数是4,其频率是 .
14.(2022秋 锦州期末)下列是根据我国历次人口普查数据,绘制的全国人口年平均增长率的折线图,根据图中提供的信息,可以判断我国人口年平均增长率的变化趋势是逐渐 .(填“下降”或“上升”)
15.(2022秋 南县期末)为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查,整理样本数据,得到如表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区15000名初中学生视力不低于4.8的人数是 .
16.(2022秋 市北区期末)一个不透明袋子中装有30个小球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中随机摸出1个球,记下颜色后放回搅匀,并重复该过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.3600 0.3100 0.3250 0.3340 0.3325 0.3335
该学习小组发现,摸到红球的频率在一个常数附近波动,由此估算出红球个数是 个.
三.解答题(共4小题)
17.(2022 邓州市一模)某校为了解学生对我国社会主义现代化建设中“两个一百年”奋斗目标的知晓情况,对全校学生进行了相关知识测试(满分为100分),并从七、八年级各随机抽取了10名同学的成绩,收集数据为:
七年级:90,95,95,80,90,80,85,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90;
整理数据:
分数人数年级 80 85 90 95 100
七年级 2 2 3 2 1
八年级 1 2 a 2 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 90 90 c 30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c的值;
(2)通过数据分析你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次测试成绩不低于90分的为“优秀“,估计这两个年级共有多少名学生达到“优秀”.
18.(2023春 温州期末)为丰富学生的课余生活,培养学生的爱好,陶冶学生的情操,某校开展学生拓展课,为了解学生各社团活动的参与人数,该校对参与社团活动的学生进行了抽样调查,制作出如下的统计图根据该统计图,完成以下问题:
(1)这次共调查了 名学生;
(2)请把统计图1补充完整;
(3)已知该校七年级共有680名学生参加社团活动,请根据样本估算该校七年级学生参加艺术类社团的人数
19.(2022 温州校级模拟)在推进城乡生活垃圾分类的行动中,社区从A,B两个小区各随机选择50位居民进行问卷调查,并得到他们的成绩,将成绩a<60定为“不了解”,60<a≤80为“比较了解”,80<a≤100为“非常了解“,并绘制了如图的统计图:
(每一组不包含前一个边界值,包含后一个边界值)
已知A小区共有常住居民500人,B小区共有常住居民400人,
(1)请估计整个B小区达到“非常了解”的居民人数.
(2)将“比较了解”和“非常了解”的人数作为普及到位的居民,请估计整个A小区普及到位的居民人数.
(3)你认为哪个小区垃圾分类的普及工作更出色?请通过计算并用合适的数据来说明.
20.(2023春 敦化市期末)某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐;B.去影院看电影;C.到公园游玩;D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成统计图.根据统计图提供的信息,解答下列问题:
(1)请直接写出n的值; ;
(2)四种方式中最受学生喜欢的方式为 (用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 ;
(3)根据统计结果,估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
2022-2023学年初中数学六年级下学期经典精练之数据的收集、整理与描述
一.选择题(共10小题)
1.(2022秋 驻马店期末)下列说法中,正确的是( )
A.了解你们班同学周末时间如何按需要进行抽样检查
B.了解全国中学生的节水意识需要进行普查
C.神舟飞船发射前需要对零部件进行抽样检查
D.了解某种节能灯的使用寿命适合抽样调查
【考点】抽样调查的可靠性.
【专题】数据的收集与整理;数据分析观念.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【解答】解:A、了解你们班同学周末时间是如何安排的,适合普查,故不符合题意;
B、了解全国中学生的节水意识,工作量较大,且没有必要,适合抽样调查,故不符合题意;
C、神舟飞船发射前需要对零部件进行全面调查,故不符合题意;
D、了解某种节能灯的使用寿命适合抽样调查,故符合题意.
故选:D.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.(2021秋 仁寿县期末)新型冠状病毒肺炎(CoronaVriusDisease2019,COVID﹣19),简称“新冠肺炎”,世界卫生组织命名为“2019冠状病毒病”,英文单词CoronaVriusDisease中字母r出现的频数是( )
A.2 B.11.1% C.18 D.
【考点】频数与频率.
【专题】数据的收集与整理;数据分析观念.
【分析】根据CoronaVriusDisease中共有18个字母,其中r出现2次可得答案.
【解答】解:CoronaVriusDisease中共有18个字母,其中r出现2次,
∴频数是2,
故选:A.
【点评】本题考查频数的定义,熟练掌握频数的定义是解题关键.
3.(2022秋 新都区期末)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
【考点】频数(率)分布直方图;频数(率)分布折线图;统计图的选择.
【专题】统计的应用;数据分析观念.
【分析】根据三种统计图的特点判断即可.
【解答】解:最宜反映人体体温变化的是:折线统计图,
故选:A.
【点评】本题考查了统计图的选择,频数分布直方图,频数分布折线图,熟练掌握三种统计图的特点是解题的关键.
4.(2022秋 太原期末)一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
【考点】用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【分析】估计利用频率估计概率可估计摸到红球的概率为0.7,然后根据概率公式计算这个口袋中红球的数量.
【解答】解:因为共摸了200次球,发现有140次摸到红球,
所以估计摸到红球的概率为0.7,
所以估计这个口袋中红球的数量为10×0.7=7(个).
故选:D.
【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
5.(2022秋 胶州市期末)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.组距为10
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
【考点】频数(率)分布表;频数(率)分布直方图.
【专题】数据的收集与整理;统计的应用;数据分析观念;运算能力.
【分析】根据条形统计图所表示的意义逐项进行判断即可.
【解答】解:从条形统计图可知,
得分在70~80分的人数最多,是14人,因此选项A不符合题意;
组距为60﹣50=70﹣60=80﹣70=90﹣80=10,因此选项B不符合题意;
人数最少的是“90﹣100”分数段的,是2人,因此选项C不符合题意;
得分及格(≥60)的有12+14+8+2=36(人),因此选项D符合题意;
故选:D.
【点评】本题考查频数分布直方图,理解条形统计图所表示数据的特征是正确判断的前提.
6.(2022秋 海淀区校级期中)小明同学统计了某学校八年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示.下面有四个推断:
①小明此次一共调查了100位同学;
②每天阅读图书时间不足15分钟的同学人数多于45﹣60分钟的人数;
③每天阅读图书时间在15﹣30分钟的人数最多;
④每天阅读图书时间超过30分钟的同学人数是调查总人数的20%.
根据图中信息,上述说法中正确的是( )
A.①③ B.①④ C.②③ D.②④
【考点】频数(率)分布直方图.
【专题】数据的收集与整理;统计的应用;数据分析观念.
【分析】根据频数分布直方图中的数据,可以判断各个小题中的说法是否正确,从而可以解答本题.
【解答】解:由直方图可得,
小明此次一共调查了10+60+20+10=100名同学,故①正确;
每天阅读图书时间不足15分钟的同学人数和45﹣60分钟的人数一样多,故②错误;
每天阅读图书时间在15﹣30分钟的人数最多,故③正确;
每天阅读图书时间超过30分钟的同学人数是调查总人数的:(20+10)÷100×100%=30%,故④错误;
故选:A.
【点评】本题考查频数分布直方图,利用数形结合的思想解答是解答本题的关键.
7.(2022秋 长沙期末)长沙网红打卡点铜官窑古镇为迎接“五一”假期新增了骑马、威亚、卡丁车、低空飞行4项互动体验项目,并对部分游客所喜欢的项目进行调查问卷(每个游客均只选择一个喜欢的项目),统计如图,其中喜欢威亚的有80人,则本次调查的游客有( )人.
A.120 B.160 C.300 D.400
【考点】扇形统计图.
【专题】统计的应用;运算能力.
【分析】根据喜欢威亚的人数和所占的百分比即可得出答案.
【解答】解:本次调查的游客人数有;80÷20%=400(人).
故选:D.
【点评】本题考查的是扇形统计图.读懂统计图,从扇形统计图中得到相关的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.
8.(2022秋 成华区期末)绿水青山就是金山银山.如图为成都部分区县森林覆盖率统计图,其中森林覆盖率高于50%的区县有( )
A.2个 B.3个 C.4个 D.5个
【考点】条形统计图.
【专题】数据的收集与整理;数据分析观念.
【分析】由条形图中森林覆盖率高于50%的城市有浦江县、都江堰、大邑县可得答案.
【解答】解:由条形图中森林覆盖率高于50%的城市有浦江县、都江堰、大邑县,
故选:B.
【点评】本题主要考查条形统计图,解题的关键是掌握条形图的特点:从条形图可以很容易看出数据的大小,便于比较.
9.(2022秋 罗湖区期末)如图是某超市2017~2021年的销售额及其增长率的统计图,下面说法中正确的是( )
A.这5年中,销售额先增后减再增
B.这5年中,增长率先变大后变小
C.这5年中,销售额一直增加
D.这5年中,2021年的增长率最大
【考点】折线统计图.
【专题】统计的应用;应用意识.
【分析】根据折线统计图的意义解答.
【解答】解:根据折线统计图可知,这5年中,销售额在增大,增长率先增后减再增,2018年的增长率最大.
故选:C.
【点评】本题考查了折线统计图,要分析清楚折线统计图的意义.
10.(2022秋 仁寿县期末)已知一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率是( )
A.20% B.40% C.60% D.80%
【考点】算术平方根;无理数;频数与频率.
【专题】统计的应用.
【分析】根据频率的定义解决问题即可.
【解答】解:一组数据:π,﹣,,0.1010010001,,其中无理数出现的频率==40%,
故选:B.
【点评】本题考查频数与频率,无理数,有理数等知识,解题的关键是理解频率的定义,属于中考常考题型.
二.填空题(共6小题)
11.(2022秋 白银期末)某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是 样本 .(填“总体”,“样本”或“个体”)
【考点】总体、个体、样本、样本容量.
【专题】数据的收集与整理;数据分析观念.
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.
【解答】解:某市今年共有12万名考生参加中考,为了了解这12万名考生的数学成绩,从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中,被抽取的1500名考生的数学成绩是样本.
故答案为:样本.
【点评】本题考查的是确定总体、个体和样本.解此类题需要注意考察对象实际应是表示事物某一特征的数据,而非考查的事物.
12.(2022秋 新都区期末)成都市于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾,可回收物,其他垃圾和有害垃圾四类.通过调查某小区四类垃圾的比例,整理制作出如图扇形图,若某个月该小区产生各类垃圾共80吨,其中可回收物有 20.8 吨.
【考点】扇形统计图.
【专题】统计的应用;数据分析观念;运算能力.
【分析】由扇形统计图可知,“可回收垃圾”占垃圾总量的26%,求出80吨的26%即可.
【解答】解:由扇形统计图可知,“可回收垃圾”占垃圾总量的26%,
即80×26%=20.8(吨),
故答案为:20.8.
【点评】本题考查扇形统计图,理解扇形统计图中各个部分所占整体的百分比是解决问题的关键.
13.(2022秋 沈丘县期末)一组数据4,﹣4,,4,,4,﹣4,4中,出现次数最多的数是4,其频率是 0.5 .
【考点】频数与频率.
【专题】概率及其应用;数据分析观念.
【分析】用4出现的次数除以数据的个数即可.
【解答】解:4出现的频率是4÷8=0.5.
故答案为:0.5.
【点评】本题考查了频数与频率:频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
14.(2022秋 锦州期末)下列是根据我国历次人口普查数据,绘制的全国人口年平均增长率的折线图,根据图中提供的信息,可以判断我国人口年平均增长率的变化趋势是逐渐 下降 .(填“下降”或“上升”)
【考点】折线统计图.
【专题】数据的收集与整理;数据分析观念.
【分析】折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.
【解答】解:根据折线统计图可知,我国人口年平均增长率的变化趋势是逐渐下降.
故答案为:下降.
【点评】本题考查的是折线统计图.读懂统计图并从统计图中得到必要的信息是解决问题的关键.
15.(2022秋 南县期末)为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查,整理样本数据,得到如表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区15000名初中学生视力不低于4.8的人数是 9000人 .
【考点】用样本估计总体.
【专题】统计的应用;数据分析观念.
【分析】用总人数乘以样本中视力不低于4.8的人数所占比例即可.
【解答】解:估计该区15000名初中学生视力不低于4.8的人数是15000×=9000(人),
故答案为:9000人.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
16.(2022秋 市北区期末)一个不透明袋子中装有30个小球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中随机摸出1个球,记下颜色后放回搅匀,并重复该过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.3600 0.3100 0.3250 0.3340 0.3325 0.3335
该学习小组发现,摸到红球的频率在一个常数附近波动,由此估算出红球个数是 10 个.
【考点】用样本估计总体;频数与频率.
【专题】统计的应用;应用意识.
【分析】通过表格中数据,随着次数的增多,摸到白球的频率越稳定在0.3335左右,估计得出答案.
【解答】解:由题意摸到白球的频率在一个常数附近摆动,这个常数是0.3335,
由此估出红球有30×0.3335≈10(个).
故答案为:10.
【点评】本题考查频数与频率,解题的关键是掌握频率的定义,属于中考常考题型.
三.解答题(共4小题)
17.(2022 邓州市一模)某校为了解学生对我国社会主义现代化建设中“两个一百年”奋斗目标的知晓情况,对全校学生进行了相关知识测试(满分为100分),并从七、八年级各随机抽取了10名同学的成绩,收集数据为:
七年级:90,95,95,80,90,80,85,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90;
整理数据:
分数人数年级 80 85 90 95 100
七年级 2 2 3 2 1
八年级 1 2 a 2 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 90 90 c 30
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c的值;
(2)通过数据分析你认为哪个年级的成绩比较好?请说明理由;
(3)该校七、八年级共有600人,本次测试成绩不低于90分的为“优秀“,估计这两个年级共有多少名学生达到“优秀”.
【考点】用样本估计总体.
【专题】统计的应用;应用意识.
【分析】(1)根据八年级抽取的10名同学的成绩求出a的值,根据中位数和众数的概念求出b,c的值;
(2)比较七、八年级的平均数、中位数、众数以及方差的大小,即可得出答案;
(3)用600乘以样本中七、八年级测试成绩不低于90分所占的比例即可.
【解答】解:(1)由题意可得,a=4.
将七年级抽样成绩重新排列为:80,80,85,85,90,90,90,95,95,100,
位于中间位置的两个数都是90,所以中位数b==90,
90出现了3次,次数最多,所以众数c=90;
(2)八年级的成绩比较好.理由如下:
虽然七、八年级成绩的中位数与众数相同,但是八年级的成绩的平均数比七年级高,方差比七年级小,
所以八年级的成绩比较好;
(3)600×=390(人),
故估计这两个年级共有390名学生达到“优秀”.
【点评】本题考查中位数、众数、平均数、方差以及用样本估计总体,解答本题的关键是明确题意,掌握中位数、众数、平均数、方差的意义.
18.(2023春 温州期末)为丰富学生的课余生活,培养学生的爱好,陶冶学生的情操,某校开展学生拓展课,为了解学生各社团活动的参与人数,该校对参与社团活动的学生进行了抽样调查,制作出如下的统计图根据该统计图,完成以下问题:
(1)这次共调查了 80 名学生;
(2)请把统计图1补充完整;
(3)已知该校七年级共有680名学生参加社团活动,请根据样本估算该校七年级学生参加艺术类社团的人数
【考点】用样本估计总体.
【专题】统计的应用;运算能力.
【分析】(1)根据A社团的人数和所占的百分比即可得出答案;
(2)用总人数减去其他社团的人数,求出B社团的人数,从而补全统计图;
(3)用总人数乘以参加艺术类社团的人数所占的百分比即可.
【解答】解:(1)这次共调查的学生有:32÷40%=80(名).
故答案为:80;
(2)B社团的人数有:80﹣32﹣24﹣8=16(名),补全统计图如下:
(3)680×=136(名),
答:估算该校七年级学生参加艺术类社团的人数有136名.
【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
19.(2022 温州校级模拟)在推进城乡生活垃圾分类的行动中,社区从A,B两个小区各随机选择50位居民进行问卷调查,并得到他们的成绩,将成绩a<60定为“不了解”,60<a≤80为“比较了解”,80<a≤100为“非常了解“,并绘制了如图的统计图:
(每一组不包含前一个边界值,包含后一个边界值)
已知A小区共有常住居民500人,B小区共有常住居民400人,
(1)请估计整个B小区达到“非常了解”的居民人数.
(2)将“比较了解”和“非常了解”的人数作为普及到位的居民,请估计整个A小区普及到位的居民人数.
(3)你认为哪个小区垃圾分类的普及工作更出色?请通过计算并用合适的数据来说明.
【考点】调查收集数据的过程与方法;用样本估计总体.
【专题】数据的收集与整理;数据分析观念;运算能力.
【分析】(1)用整个B小区总人数乘以样本中“非常了解”的人数的百分比,即可估计整个B小区达到“非常了解”的居民人数;
(2)用整个A小区总人数乘以样本中“比较了解”和“非常了解”的人数的频率,即可估计整个A小区普及到位的居民人数;
(3)计算出两个小区样本“不了解”的人数的百分比,用样本估计总体
【解答】解:(1)估计整个B小区达到“非常了解”的居民人数有:400×24%=96(人);
(2)整个A小区普及到位的居民人数有:500×=250(人);
(3)因为整个A小区“不了解”的=50%,500×50%=250(人);
整个B小区“不了解”的44%,44%×400=176(人).
所以B小区垃圾分类的普及工作更出色.
【点评】本题考查了用样本估计总体,调查收集数据的过程与方法,解决本题的关键是掌握用样本估计总体.
20.(2023春 敦化市期末)某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐;B.去影院看电影;C.到公园游玩;D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成统计图.根据统计图提供的信息,解答下列问题:
(1)请直接写出n的值; 200 ;
(2)四种方式中最受学生喜欢的方式为 C (用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 35% ;
(3)根据统计结果,估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
【考点】全面调查与抽样调查;用样本估计总体.
【专题】统计的应用;运算能力.
【分析】(1)根据条形图,把A,B,C,D的人数加起来,即可解答;
(2)C的学生人数最多,即为四种方式中最受学生喜欢的方式;用C的人数÷总人数,即可得到百分比;
(3)用该校的总人数乘以喜欢C方式的学生比喜欢B方式的学生多占的百分比即可.
【解答】解:(1)n=30+40+70+60=200.
故答案为:200;
(2)∵C的学生人数最多,
∴四种方式中最受学生喜欢的方式为C,
×100%=35%,
故答案为:C,35%.
(3)1200×(﹣)=180(人),
答:估计该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多的人数为180人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
