2022届芜湖市(九年级)初三下学期开学摸底考试卷【含答案】
文档属性
| 名称 | 2022届芜湖市(九年级)初三下学期开学摸底考试卷【含答案】 |  | |
| 格式 | zip | ||
| 文件大小 | 370.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 10:16:48 | ||
图片预览

文档简介
2022 届初三下学期开学摸底考试卷
数学
(满分 150 分)
一、选择题(本大题共 10小题,每小题 4分,共 40分。)
1 2 3 4 5 6 7 8 9 10
1.对于任何有理数 a,下列各式中一定为负数的是( ).
A. ( 3 a) B. a C. a 1 D. a 1
2. (xn 1)2 (x2 )n 1 ( )
A. x4n B. x4n+3 C. x4n+1 D. x4n-1
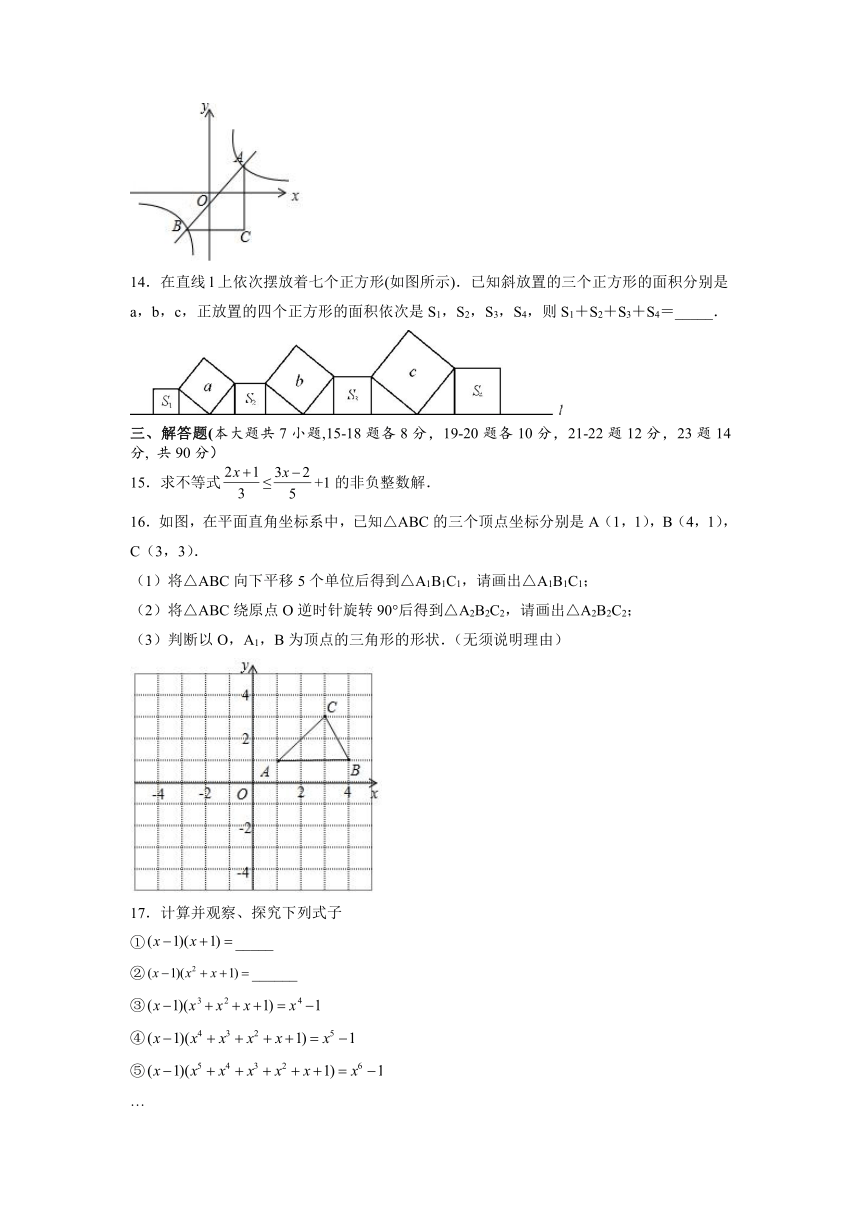
3.如图所示的几何体,它的左视图是( )
A. B. C. D.
4.习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约 11700000人,
将数据 11700000用科学记数法表示为( )
A.1.17×107 B.11.7×106 C.0.117×107 D.1.17×108
5.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194 .现用
一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员的身高
( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
6.如图,函数 y=2x和 y=ax+4的图象相交于 A(m,3),则不等式 2x< ax+4的解集为( )
A x > 3. B. x > 3 C. x < 3 D. x < 3
2 2
7.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为 1,则 tan∠BAC的值为
( )
A 1. 2 B.1 C
3
. D. 3
3
8.关于二次函数 y 2x2 4x 1,下列说法正确的是( )
A.图像与 y轴的交点坐标为 0,1 B.图像的对称轴在 y轴的右侧
C.当 x 0时, y的值随 x值的增大而减小 D. y的最小值为-3
9.已知⊙O的直径 CD=10cm,AB是⊙O的弦,AB=8cm,且 AB⊥CD,垂足为M,则 AC
的长为( )
A.2 5 cm B.4 5 cm C.2 5 cm或 4 5 cm D.2 3 cm或 4 3 cm
10.如图, ABC中, ACB 90 , A 30 ,AB 16,点 P是斜边 AB上任意一点,
过点 P作PQ AB,垂足为 P,交边AC(或边CB)于点 Q,设AP x, APQ的面积为 y,
则 y与 x之间的函数图象大致是 ( )
A. B. C. D.
二、填空题(本大题共 4小题,每小题 5分,20分)
a2 1 1 a211.若 a、b为实数,且 b= +4,则 a+b=_____.
a 7
12.因式分解: x﹣3 2x2 y xy2 __________.
3
13.如图,直线 y=x+m与双曲线 y= 相交于 A,B两点,BC∥x轴,AC∥y轴,则△ABC
x
面积的最小值为_____.
14.在直线 l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是
a,b,c,正放置的四个正方形的面积依次是 S1,S2,S3,S4,则 S1+S2+S3+S4=_____.
三、解答题(本大题共 7 小题,15-18 题各 8 分,19-20 题各 10 分,21-22 题 12 分,23 题 14
分, 共 90分)
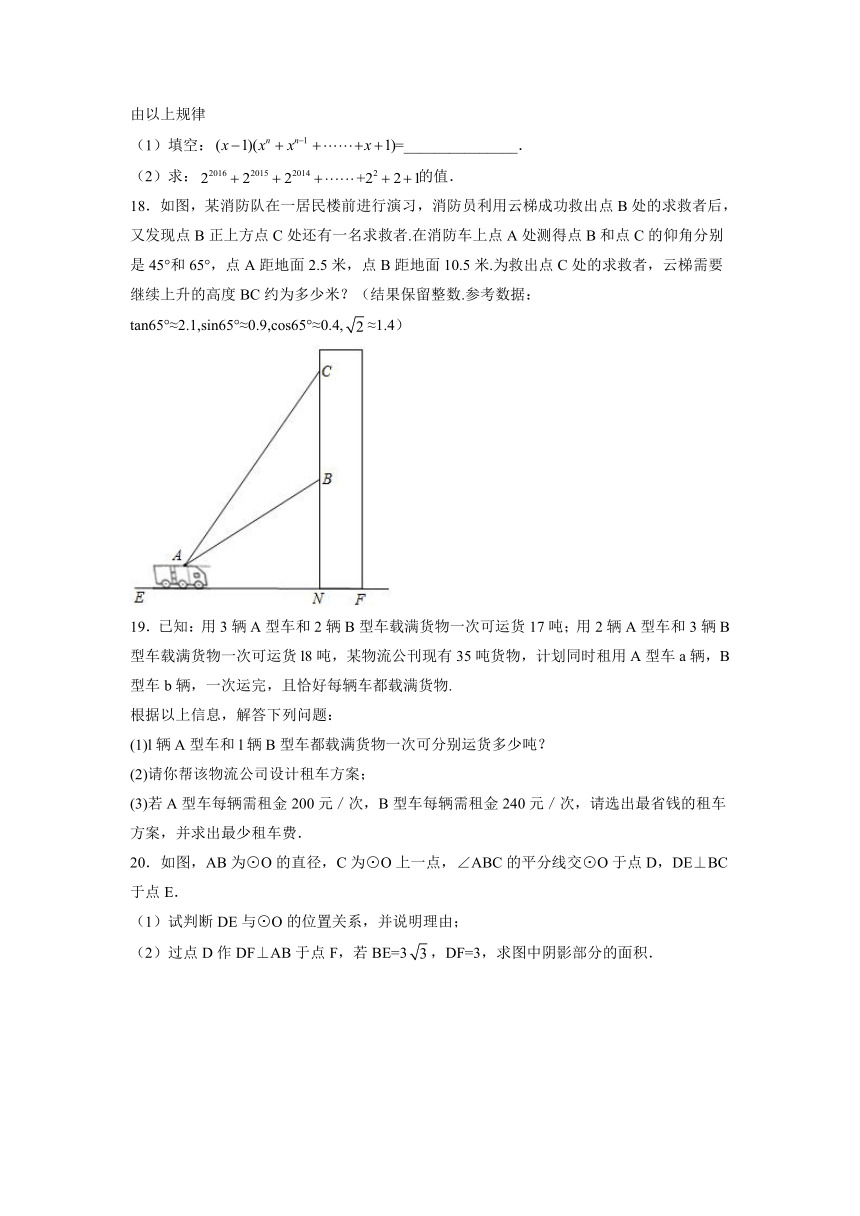
2x 1 3x 2
15.求不等式 ≤ +1的非负整数解.
3 5
16.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是 A(1,1),B(4,1),
C(3,3).
(1)将△ABC向下平移 5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点 O逆时针旋转 90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以 O,A1,B为顶点的三角形的形状.(无须说明理由)
17.计算并观察、探究下列式子
① (x 1)(x 1) _____
② (x 1)(x2 x 1) ______
③ (x 1)(x3 x 2 x 1) x 4 1
④ (x 1)(x4 x3 x2 x 1) x5 1
⑤ (x 1)(x5 x4 x3 x2 x 1) x6 1
…
由以上规律
(1)填空: (x 1)(xn xn 1 x 1)=_______________.
(2)求: 22016 22015 22014 +22 2 1的值.
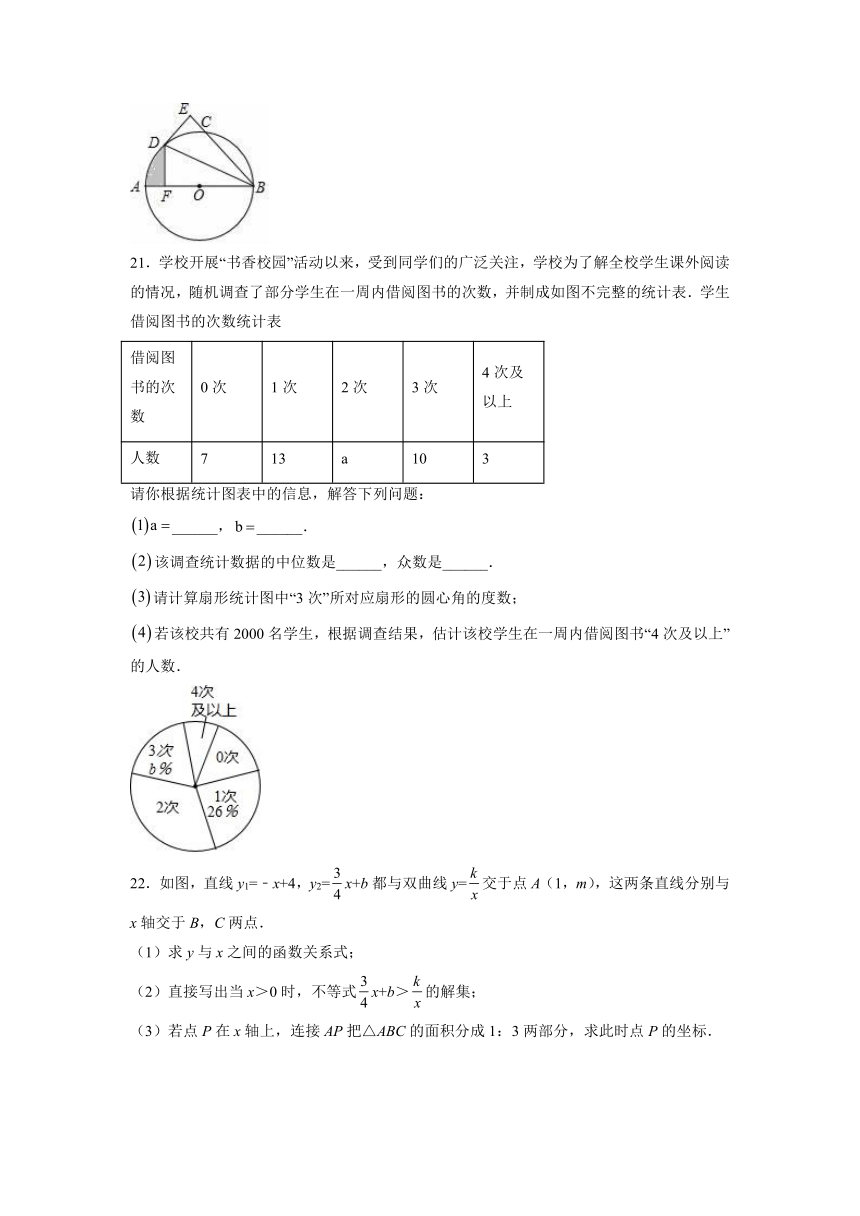
18.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 B处的求救者后,
又发现点 B正上方点 C处还有一名求救者.在消防车上点 A处测得点 B和点 C的仰角分别
是 45°和 65°,点 A距地面 2.5米,点 B距地面 10.5米.为救出点 C处的求救者,云梯需要
继续上升的高度 BC约为多少米?(结果保留整数.参考数据:
tan65°≈2.1,sin65°≈0.9,cos65°≈0.4, 2 ≈1.4)
19.已知:用 3辆 A型车和 2辆 B型车载满货物一次可运货 17吨;用 2辆 A型车和 3辆 B
型车载满货物一次可运货 l8吨,某物流公刊现有 35吨货物,计划同时租用 A型车 a辆,B
型车 b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆 A型车和 l辆 B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若 A型车每辆需租金 200元/次,B型车每辆需租金 240元/次,请选出最省钱的租车
方案,并求出最少租车费.
20.如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点 D,DE⊥BC
于点 E.
(1)试判断 DE与⊙O的位置关系,并说明理由;
(2)过点 D作 DF⊥AB于点 F,若 BE=3 3,DF=3,求图中阴影部分的面积.
21.学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读
的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生
借阅图书的次数统计表
借阅图
4次及
书的次 0次 1次 2次 3次
以上
数
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
1 a ______,b ______.
2 该调查统计数据的中位数是______,众数是______.
3 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
4 若该校共有 2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”
的人数.
3 k
22.如图,直线 y1=﹣x+4,y2= x+b都与双曲线 y= 交于点 A(1,m),这两条直线分别与4 x
x轴交于 B,C两点.
(1)求 y与 x之间的函数关系式;
3 k
(2)直接写出当 x>0时,不等式 x+b> 的解集;
4 x
(3)若点 P在 x轴上,连接 AP把△ABC的面积分成 1:3两部分,求此时点 P的坐标.
23.如图(1),已知点 G在正方形 ABCD的对角线 AC上,GE⊥BC,垂足为点 E,GF⊥CD,
垂足为点 F.
(1)证明与推断:
①求证:四边形 CEGF 是正方形;
AG
②推断: 的值为 :
BE
(2)探究与证明:
将正方形 CEGF绕点 C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段 AG
与 BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形 CEGF 在旋转过程中,当 B,E,F三点在一条直线上时,如图(3)所示,延长 CG
交 AD于点 H.若 AG=6,GH=2 2,则 BC= .
2022 届初三下学期开学摸底考试卷
数学 参考答案
(满分 150 分)
二、选择题(本大题共 10小题,每小题 4分,共 40分。)
1 2 3 4 5 6 7 8 9 10
D A D A A C B D C D
二、填空题(本大题共 4小题,每小题 5分,20分)
11. 【答案】5或 3
12 2. 【答案】 x x y
13. 【答案】6
14. 【答案】a+c
三、解答题(本大题共 7 小题,17-18 题各 8 分,19-20 题各 10 分,21-22 题 12 分,23 题 14
分, 共 90分)
15. 【答案】不等式的非负整数解为 0、1、2、3、4.
【详解】
去分母得:5(2x+1)≤3(3x-2)+15,
去括号得:10x+5≤9x-6+15,
移项得:10x-9x≤-5-6+15,
合并同类项得 x≤4,
∴不等式的非负整数解为 0、1、2、3、4.
16.【答案】(1)画图见解析;(2)画图见解析;(3)三角形的形状为等腰直角三角形.
【详解】(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)三角形的形状为等腰直角三角形,OB=OA1= 42 12 17,
A1B= 52 32 = 34,
即 OB2+OA12=A1B2,
所以三角形的形状为等腰直角三角形.
17. 【答案】① x2 1;② x3 1;
(1) xn 1 1
(2)22017-1
【详解】
(1) ;
(2)( 22016 22015 22014 +22 2 1)
=(2-1) (22016 22015 22014 +22 2 1)
=22017-1.
18.【答案】云梯需要继续上升的高度 BC约为 9米.
【详解】
过点A作 AM EF 于点M , AD BC于点D,
∵CN EF ,
∴ AMN MND ADN 90 ,
∴四边形 AMND为矩形.
∴DN AM 2.5米.
∴ BD BN DN 10.5 2.5 8(米),
由题意可知, BAD 45 , CAD 65 ,
∵ AD BC,
∴ ADB 90 ,
在 Rt ABD中, tan BAD
BD
,
AD
AD BD 8∴ 8(米).
tan BAD tan45
CD
在 Rt ACD中, tan CAD ,
AD
∴CD AD tan CAD 8tan65 8 2.1 16.8(米).
∴ BC CD BD 16.8 8 8.8 9(米).
答:云梯需要继续上升的高度 BC约为 9米.
19. 【答案】(1) A型车、B型车都装满货物一次可以分别运货 3吨、4吨;(2) 最省钱的租
车方案是方案一:A型车 8辆,B型车 2辆,最少租车费为 2080元.
【详解】
解:(1)设每辆 A型车、B型车都装满货物一次可以分别运货 x吨、y吨,
3x 2y 17
依题意列方程组为:
2x 3y 18
x 3
解得
y 4
答:1辆 A型车辆装满货物一次可运 3吨,1辆 B型车装满货物一次可运 4吨.
(2)结合题意,和(1)可得 3a+4b=35
35 4b
∴a=
3
∵a、b都是整数
a 9 a 5 a 1
∴ 或 或
b 2
b 5 b 8
答:有 3种租车方案:
方案一:A型车 9辆,B型车 2辆;
方案二:A型车 5辆,B型车 5辆;
方案三:A型车 1辆,B型车 8辆.
(3)∵A型车每辆需租金 200元/次,B型车每辆需租金 240元/次,
∴方案一需租金:9×200+2×240=2280(元)
方案二需租金:5×200+5×240=2200(元)
方案三需租金:1×200+8×240=2120(元)
∵2280>2200>2120
∴最省钱的租车方案是方案一:A型车 1辆,B型车 8辆,最少租车费为 2120元.
20.【答案】(1)DE与⊙O 3 3相切,理由见解析;(2)阴影部分的面积为 2π﹣ .
2
【详解】
(1)DE与⊙O相切,
理由:连接 DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点 D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)∵∠ABC的平分线交⊙O于点 D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3 3,
∴BD= 32+(3 3)2 =6,
3 1
∵sin∠DBF= = ,
6 2
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°= DF 3 3 ,
DO DO 2
∴DO=2 3,
则 FO= 3,
60 (2 3)2 1 3 3
故图中阴影部分的面积为: 3 3 2 .
360 2 2
21.【答案】 1 17、20; 2 2次、2次; 3 72 ; 4 120人.
【详解】
1 被调查的总人数为13 26% 50人,
a 50 7 13 10 3 17, b% 10 100% 20%,即 b 20,
50
故答案为 17、20;
2 由于共有 50个数据,其中位数为第 25、26个数据的平均数,
而第 25、26个数据均为 2次,
所以中位数为 2次,
出现次数最多的是 2次,
所以众数为 2次,
故答案为 2次、2次;
3 扇形统计图中“3次”所对应扇形的圆心角的度数为360 20% 72 ;
4 3估计该校学生在一周内借阅图书“4次及以上”的人数为 2000 120人.
50
5 9
22 3.【答案】(1) y ;(2)x>1;(3)P(﹣ ,0)或( ,0)
x 4 4
【详解】
(1)把 A(1,m)代入 y1=﹣x+4,可得 m=﹣1+4=3,
∴A(1,3),
k
把 A(1,3)代入双曲线 y= ,可得 k=1×3=3,
x
3
∴y与 x之间的函数关系式为:y= ;
x
(2)∵A(1,3),
3 k
∴当 x>0时,不等式 x+b> 的解集为:x>1;
4 x
(3)y1=﹣x+4,令 y=0,则 x=4,
∴点 B的坐标为(4,0),
3 3
把 A(1,3)代入 y2= x+b,可得 3= +b,4 4
9
∴b= ,
4
3 9
∴y2= x+ ,4 4
令 y2=0,则 x=﹣3,即 C(﹣3,0),
∴BC=7,
∵AP把△ABC的面积分成 1:3两部分,
1 7 1 7
∴CP= BC= ,或 BP= BC=
4 4 4 4
7 5 7 9
∴OP=3﹣ = ,或 OP=4﹣ = ,
4 4 4 4
5 9
∴P(﹣ ,0)或( ,0).
4 4
23.【答案】(1)①四边形 CEGF 是正方形;② 2;(2)线段 AG与 BE之间的数量关系为
AG= 2 BE;(3)3 5
【详解】
(1)①∵四边形 ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形 CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形 CEGF是正方形;
②由①知四边形 CEGF 是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
CG
∴ 2 ,GE∥AB,
CE
AG CG
∴ 2,
BE CE
故答案为 2;
(2)连接 CG,
由旋转性质知∠BCE=∠ACG=α,
在 Rt△CEG和 Rt△CBA中,
CE 2 CB= 2、 = ,
CG 2 CA 2
CG CA
∴ = 2,
CE CB
∴△ACG∽△BCE,
AG CA
∴ 2,
BE CB
∴线段 AG与 BE之间的数量关系为 AG= 2 BE;
(3)∵∠CEF=45°,点 B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
AG GH AH
∴ ,
AC AH CH
设 BC=CD=AD=a,则 AC= 2 a,
AG GH
6 2 2则由 得 ,
AC AH 2a AH
2
∴AH= a,
3
1
则 DH=AD﹣AH= a,CH= CD2
10
3 DH
2 = a,
3
2 a
AG AH 6
∴由
3
得
AC CH 2a 10
,
a
3
解得:a=3 5,即 BC=3 5,
故答案为 3 5.
数学
(满分 150 分)
一、选择题(本大题共 10小题,每小题 4分,共 40分。)
1 2 3 4 5 6 7 8 9 10
1.对于任何有理数 a,下列各式中一定为负数的是( ).
A. ( 3 a) B. a C. a 1 D. a 1
2. (xn 1)2 (x2 )n 1 ( )
A. x4n B. x4n+3 C. x4n+1 D. x4n-1
3.如图所示的几何体,它的左视图是( )
A. B. C. D.
4.习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约 11700000人,
将数据 11700000用科学记数法表示为( )
A.1.17×107 B.11.7×106 C.0.117×107 D.1.17×108
5.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194 .现用
一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员的身高
( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
6.如图,函数 y=2x和 y=ax+4的图象相交于 A(m,3),则不等式 2x< ax+4的解集为( )
A x > 3. B. x > 3 C. x < 3 D. x < 3
2 2
7.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为 1,则 tan∠BAC的值为
( )
A 1. 2 B.1 C
3
. D. 3
3
8.关于二次函数 y 2x2 4x 1,下列说法正确的是( )
A.图像与 y轴的交点坐标为 0,1 B.图像的对称轴在 y轴的右侧
C.当 x 0时, y的值随 x值的增大而减小 D. y的最小值为-3
9.已知⊙O的直径 CD=10cm,AB是⊙O的弦,AB=8cm,且 AB⊥CD,垂足为M,则 AC
的长为( )
A.2 5 cm B.4 5 cm C.2 5 cm或 4 5 cm D.2 3 cm或 4 3 cm
10.如图, ABC中, ACB 90 , A 30 ,AB 16,点 P是斜边 AB上任意一点,
过点 P作PQ AB,垂足为 P,交边AC(或边CB)于点 Q,设AP x, APQ的面积为 y,
则 y与 x之间的函数图象大致是 ( )
A. B. C. D.
二、填空题(本大题共 4小题,每小题 5分,20分)
a2 1 1 a211.若 a、b为实数,且 b= +4,则 a+b=_____.
a 7
12.因式分解: x﹣3 2x2 y xy2 __________.
3
13.如图,直线 y=x+m与双曲线 y= 相交于 A,B两点,BC∥x轴,AC∥y轴,则△ABC
x
面积的最小值为_____.
14.在直线 l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是
a,b,c,正放置的四个正方形的面积依次是 S1,S2,S3,S4,则 S1+S2+S3+S4=_____.
三、解答题(本大题共 7 小题,15-18 题各 8 分,19-20 题各 10 分,21-22 题 12 分,23 题 14
分, 共 90分)
2x 1 3x 2
15.求不等式 ≤ +1的非负整数解.
3 5
16.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是 A(1,1),B(4,1),
C(3,3).
(1)将△ABC向下平移 5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点 O逆时针旋转 90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以 O,A1,B为顶点的三角形的形状.(无须说明理由)
17.计算并观察、探究下列式子
① (x 1)(x 1) _____
② (x 1)(x2 x 1) ______
③ (x 1)(x3 x 2 x 1) x 4 1
④ (x 1)(x4 x3 x2 x 1) x5 1
⑤ (x 1)(x5 x4 x3 x2 x 1) x6 1
…
由以上规律
(1)填空: (x 1)(xn xn 1 x 1)=_______________.
(2)求: 22016 22015 22014 +22 2 1的值.
18.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 B处的求救者后,
又发现点 B正上方点 C处还有一名求救者.在消防车上点 A处测得点 B和点 C的仰角分别
是 45°和 65°,点 A距地面 2.5米,点 B距地面 10.5米.为救出点 C处的求救者,云梯需要
继续上升的高度 BC约为多少米?(结果保留整数.参考数据:
tan65°≈2.1,sin65°≈0.9,cos65°≈0.4, 2 ≈1.4)
19.已知:用 3辆 A型车和 2辆 B型车载满货物一次可运货 17吨;用 2辆 A型车和 3辆 B
型车载满货物一次可运货 l8吨,某物流公刊现有 35吨货物,计划同时租用 A型车 a辆,B
型车 b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆 A型车和 l辆 B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若 A型车每辆需租金 200元/次,B型车每辆需租金 240元/次,请选出最省钱的租车
方案,并求出最少租车费.
20.如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点 D,DE⊥BC
于点 E.
(1)试判断 DE与⊙O的位置关系,并说明理由;
(2)过点 D作 DF⊥AB于点 F,若 BE=3 3,DF=3,求图中阴影部分的面积.
21.学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读
的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生
借阅图书的次数统计表
借阅图
4次及
书的次 0次 1次 2次 3次
以上
数
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
1 a ______,b ______.
2 该调查统计数据的中位数是______,众数是______.
3 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
4 若该校共有 2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”
的人数.
3 k
22.如图,直线 y1=﹣x+4,y2= x+b都与双曲线 y= 交于点 A(1,m),这两条直线分别与4 x
x轴交于 B,C两点.
(1)求 y与 x之间的函数关系式;
3 k
(2)直接写出当 x>0时,不等式 x+b> 的解集;
4 x
(3)若点 P在 x轴上,连接 AP把△ABC的面积分成 1:3两部分,求此时点 P的坐标.
23.如图(1),已知点 G在正方形 ABCD的对角线 AC上,GE⊥BC,垂足为点 E,GF⊥CD,
垂足为点 F.
(1)证明与推断:
①求证:四边形 CEGF 是正方形;
AG
②推断: 的值为 :
BE
(2)探究与证明:
将正方形 CEGF绕点 C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段 AG
与 BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形 CEGF 在旋转过程中,当 B,E,F三点在一条直线上时,如图(3)所示,延长 CG
交 AD于点 H.若 AG=6,GH=2 2,则 BC= .
2022 届初三下学期开学摸底考试卷
数学 参考答案
(满分 150 分)
二、选择题(本大题共 10小题,每小题 4分,共 40分。)
1 2 3 4 5 6 7 8 9 10
D A D A A C B D C D
二、填空题(本大题共 4小题,每小题 5分,20分)
11. 【答案】5或 3
12 2. 【答案】 x x y
13. 【答案】6
14. 【答案】a+c
三、解答题(本大题共 7 小题,17-18 题各 8 分,19-20 题各 10 分,21-22 题 12 分,23 题 14
分, 共 90分)
15. 【答案】不等式的非负整数解为 0、1、2、3、4.
【详解】
去分母得:5(2x+1)≤3(3x-2)+15,
去括号得:10x+5≤9x-6+15,
移项得:10x-9x≤-5-6+15,
合并同类项得 x≤4,
∴不等式的非负整数解为 0、1、2、3、4.
16.【答案】(1)画图见解析;(2)画图见解析;(3)三角形的形状为等腰直角三角形.
【详解】(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)三角形的形状为等腰直角三角形,OB=OA1= 42 12 17,
A1B= 52 32 = 34,
即 OB2+OA12=A1B2,
所以三角形的形状为等腰直角三角形.
17. 【答案】① x2 1;② x3 1;
(1) xn 1 1
(2)22017-1
【详解】
(1) ;
(2)( 22016 22015 22014 +22 2 1)
=(2-1) (22016 22015 22014 +22 2 1)
=22017-1.
18.【答案】云梯需要继续上升的高度 BC约为 9米.
【详解】
过点A作 AM EF 于点M , AD BC于点D,
∵CN EF ,
∴ AMN MND ADN 90 ,
∴四边形 AMND为矩形.
∴DN AM 2.5米.
∴ BD BN DN 10.5 2.5 8(米),
由题意可知, BAD 45 , CAD 65 ,
∵ AD BC,
∴ ADB 90 ,
在 Rt ABD中, tan BAD
BD
,
AD
AD BD 8∴ 8(米).
tan BAD tan45
CD
在 Rt ACD中, tan CAD ,
AD
∴CD AD tan CAD 8tan65 8 2.1 16.8(米).
∴ BC CD BD 16.8 8 8.8 9(米).
答:云梯需要继续上升的高度 BC约为 9米.
19. 【答案】(1) A型车、B型车都装满货物一次可以分别运货 3吨、4吨;(2) 最省钱的租
车方案是方案一:A型车 8辆,B型车 2辆,最少租车费为 2080元.
【详解】
解:(1)设每辆 A型车、B型车都装满货物一次可以分别运货 x吨、y吨,
3x 2y 17
依题意列方程组为:
2x 3y 18
x 3
解得
y 4
答:1辆 A型车辆装满货物一次可运 3吨,1辆 B型车装满货物一次可运 4吨.
(2)结合题意,和(1)可得 3a+4b=35
35 4b
∴a=
3
∵a、b都是整数
a 9 a 5 a 1
∴ 或 或
b 2
b 5 b 8
答:有 3种租车方案:
方案一:A型车 9辆,B型车 2辆;
方案二:A型车 5辆,B型车 5辆;
方案三:A型车 1辆,B型车 8辆.
(3)∵A型车每辆需租金 200元/次,B型车每辆需租金 240元/次,
∴方案一需租金:9×200+2×240=2280(元)
方案二需租金:5×200+5×240=2200(元)
方案三需租金:1×200+8×240=2120(元)
∵2280>2200>2120
∴最省钱的租车方案是方案一:A型车 1辆,B型车 8辆,最少租车费为 2120元.
20.【答案】(1)DE与⊙O 3 3相切,理由见解析;(2)阴影部分的面积为 2π﹣ .
2
【详解】
(1)DE与⊙O相切,
理由:连接 DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点 D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)∵∠ABC的平分线交⊙O于点 D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3 3,
∴BD= 32+(3 3)2 =6,
3 1
∵sin∠DBF= = ,
6 2
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°= DF 3 3 ,
DO DO 2
∴DO=2 3,
则 FO= 3,
60 (2 3)2 1 3 3
故图中阴影部分的面积为: 3 3 2 .
360 2 2
21.【答案】 1 17、20; 2 2次、2次; 3 72 ; 4 120人.
【详解】
1 被调查的总人数为13 26% 50人,
a 50 7 13 10 3 17, b% 10 100% 20%,即 b 20,
50
故答案为 17、20;
2 由于共有 50个数据,其中位数为第 25、26个数据的平均数,
而第 25、26个数据均为 2次,
所以中位数为 2次,
出现次数最多的是 2次,
所以众数为 2次,
故答案为 2次、2次;
3 扇形统计图中“3次”所对应扇形的圆心角的度数为360 20% 72 ;
4 3估计该校学生在一周内借阅图书“4次及以上”的人数为 2000 120人.
50
5 9
22 3.【答案】(1) y ;(2)x>1;(3)P(﹣ ,0)或( ,0)
x 4 4
【详解】
(1)把 A(1,m)代入 y1=﹣x+4,可得 m=﹣1+4=3,
∴A(1,3),
k
把 A(1,3)代入双曲线 y= ,可得 k=1×3=3,
x
3
∴y与 x之间的函数关系式为:y= ;
x
(2)∵A(1,3),
3 k
∴当 x>0时,不等式 x+b> 的解集为:x>1;
4 x
(3)y1=﹣x+4,令 y=0,则 x=4,
∴点 B的坐标为(4,0),
3 3
把 A(1,3)代入 y2= x+b,可得 3= +b,4 4
9
∴b= ,
4
3 9
∴y2= x+ ,4 4
令 y2=0,则 x=﹣3,即 C(﹣3,0),
∴BC=7,
∵AP把△ABC的面积分成 1:3两部分,
1 7 1 7
∴CP= BC= ,或 BP= BC=
4 4 4 4
7 5 7 9
∴OP=3﹣ = ,或 OP=4﹣ = ,
4 4 4 4
5 9
∴P(﹣ ,0)或( ,0).
4 4
23.【答案】(1)①四边形 CEGF 是正方形;② 2;(2)线段 AG与 BE之间的数量关系为
AG= 2 BE;(3)3 5
【详解】
(1)①∵四边形 ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形 CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形 CEGF是正方形;
②由①知四边形 CEGF 是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
CG
∴ 2 ,GE∥AB,
CE
AG CG
∴ 2,
BE CE
故答案为 2;
(2)连接 CG,
由旋转性质知∠BCE=∠ACG=α,
在 Rt△CEG和 Rt△CBA中,
CE 2 CB= 2、 = ,
CG 2 CA 2
CG CA
∴ = 2,
CE CB
∴△ACG∽△BCE,
AG CA
∴ 2,
BE CB
∴线段 AG与 BE之间的数量关系为 AG= 2 BE;
(3)∵∠CEF=45°,点 B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
AG GH AH
∴ ,
AC AH CH
设 BC=CD=AD=a,则 AC= 2 a,
AG GH
6 2 2则由 得 ,
AC AH 2a AH
2
∴AH= a,
3
1
则 DH=AD﹣AH= a,CH= CD2
10
3 DH
2 = a,
3
2 a
AG AH 6
∴由
3
得
AC CH 2a 10
,
a
3
解得:a=3 5,即 BC=3 5,
故答案为 3 5.
同课章节目录
