专题复习:四边形 训练(含答案)
图片预览

文档简介
专题:四边形
一 :折叠中的方程思想及数形结合思想
类型一 折叠中求角度
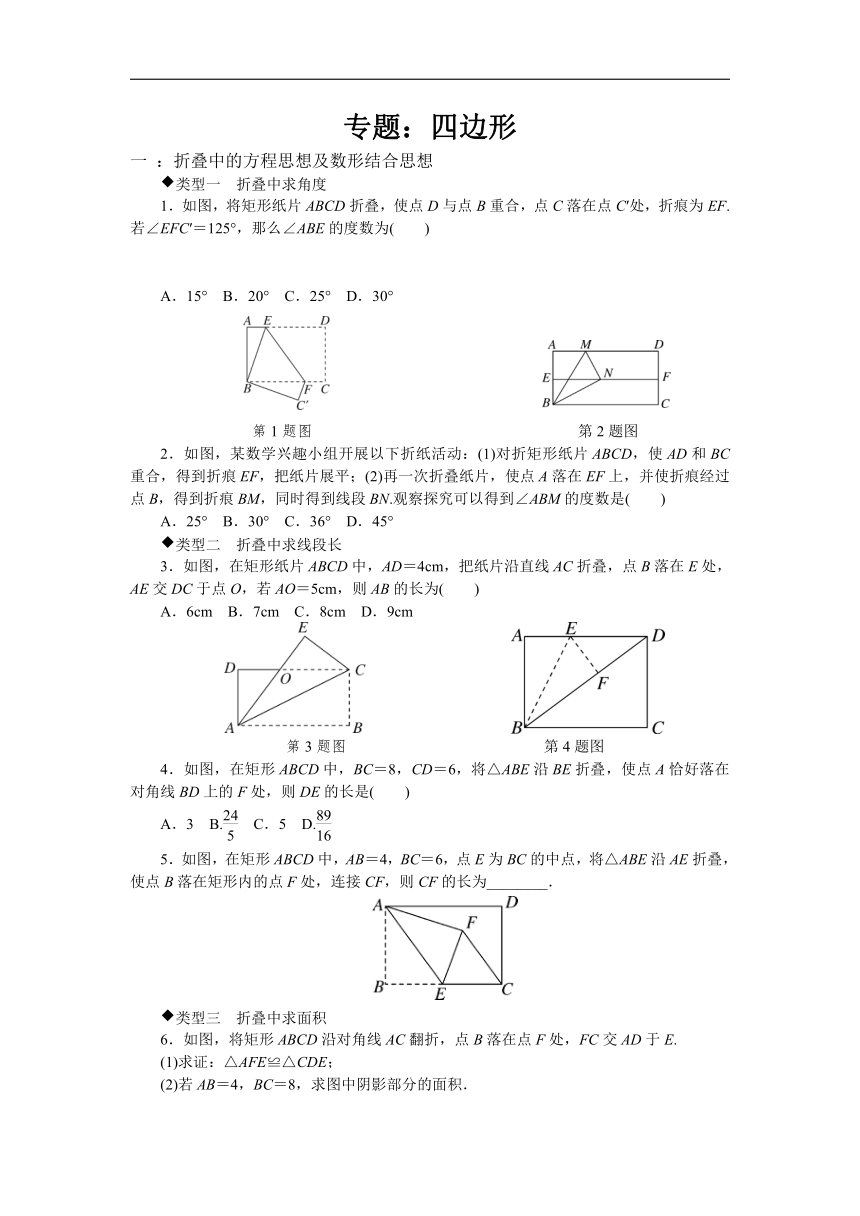
1.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF.若∠EFC′=125°,那么∠ABE的度数为( )
A.15° B.20° C.25° D.30°
第1题图 第2题图
2.如图,某数学兴趣小组开展以下折纸活动:(1)对折矩形纸片ABCD,使AD和BC重合,得到折痕EF,把纸片展平;(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN.观察探究可以得到∠ABM的度数是( )
A.25° B.30° C.36° D.45°
类型二 折叠中求线段长
3.如图,在矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.6cm B.7cm C.8cm D.9cm
第3题图 第4题图
4.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )
A.3 B. C.5 D.
5.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内的点F处,连接CF,则CF的长为________.
类型三 折叠中求面积
6.如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
7.如图,矩形ABCD中,AB=4,AD=3,M是边CD上的一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积.
二.正方形中的最值及旋转变化模型问题
类型一 利用正方形的旋转性质解题
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P,若四边形ABCD的面积是18,则DP的长是__________.
2.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.
求证:S△AEF=S△ABE+S△ADF.
3.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP.
求证:BP+CP=OP.
类型二 利用正方形的对称性解题
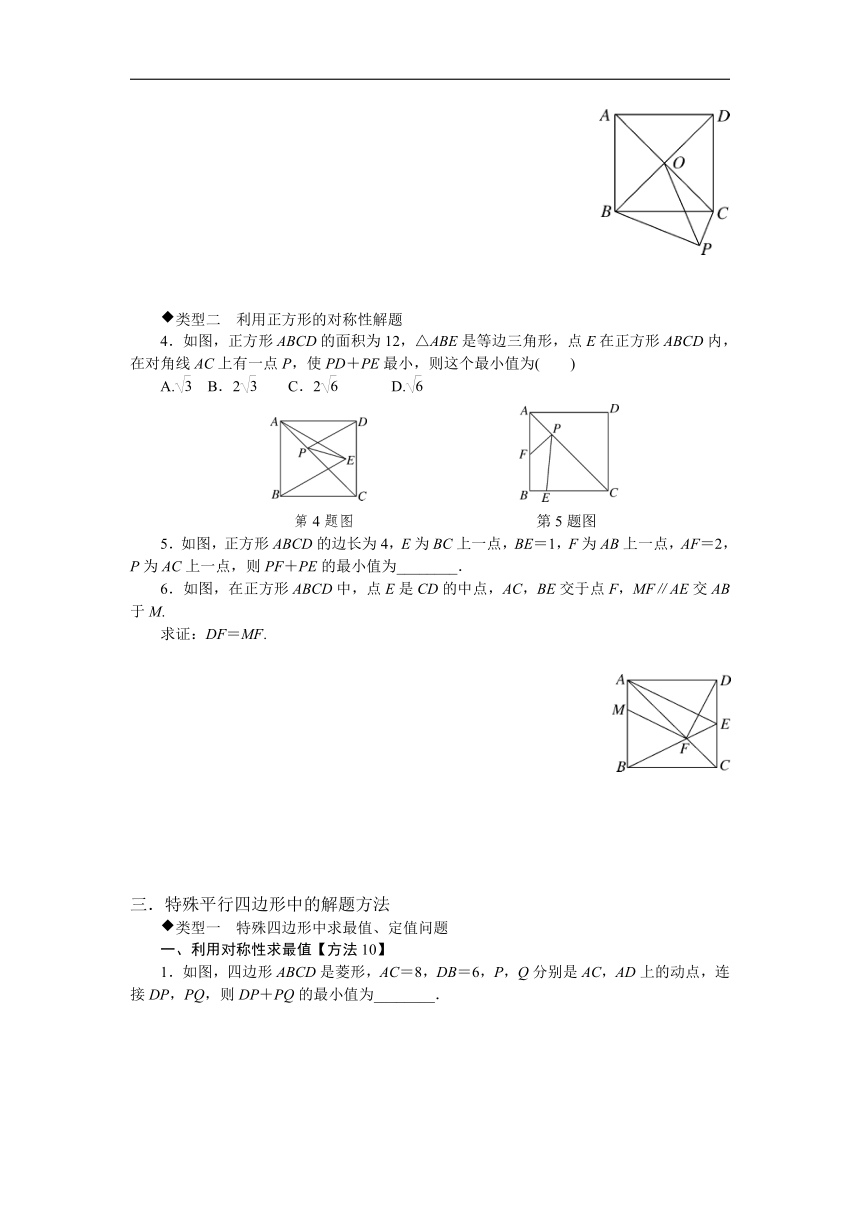
4.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. B.2 C.2 D.
第4题图 第5题图
5.如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为________.
6.如图,在正方形ABCD中,点E是CD的中点,AC,BE交于点F,MF∥AE交AB于M.
求证:DF=MF.
三.特殊平行四边形中的解题方法
类型一 特殊四边形中求最值、定值问题
一、利用对称性求最值【方法10】
1.如图,四边形ABCD是菱形,AC=8,DB=6,P,Q分别是AC,AD上的动点,连接DP,PQ,则DP+PQ的最小值为________.
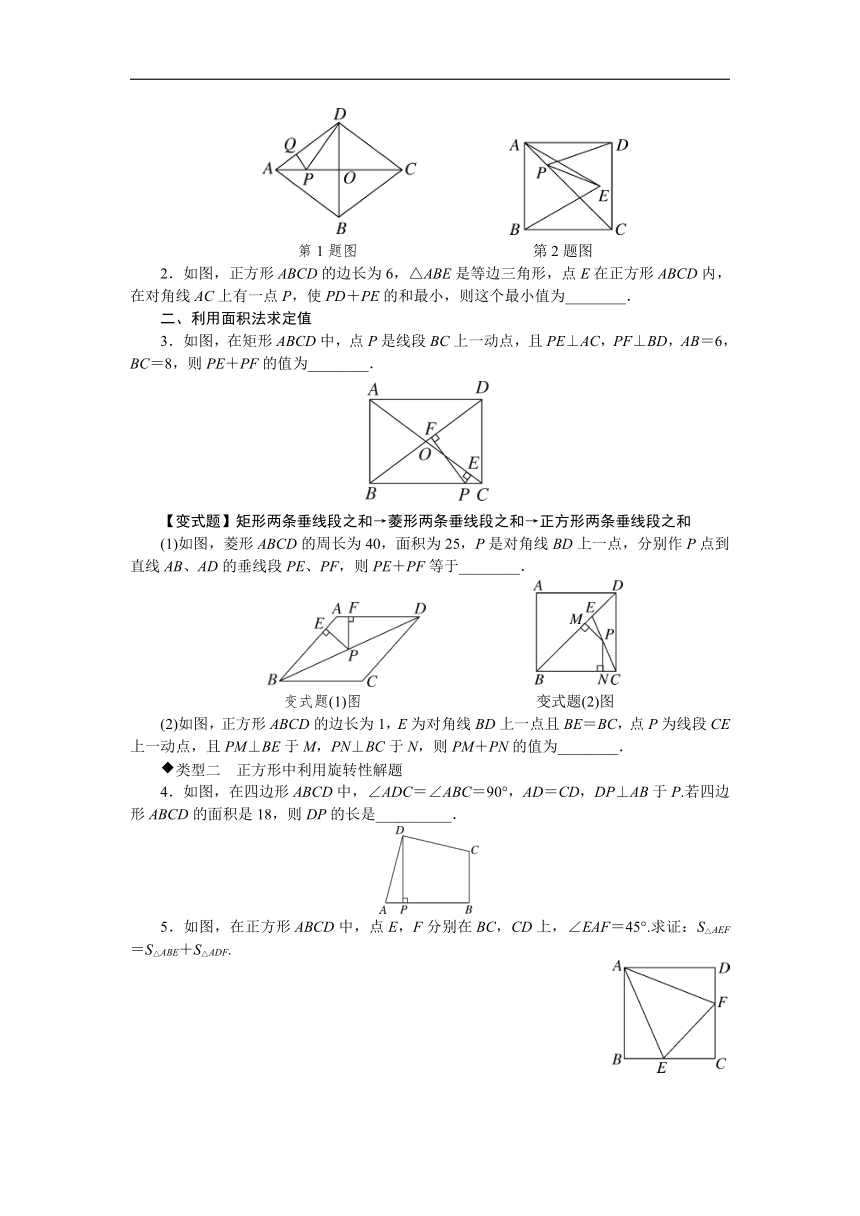
第1题图 第2题图
2.如图,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.
二、利用面积法求定值
如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,AB=6,BC=8,则PE+PF的值为________.
【变式题】矩形两条垂线段之和→菱形两条垂线段之和→正方形两条垂线段之和
(1)如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于________.
变式题(1)图 变式题(2)图
(2)如图,正方形ABCD的边长为1,E为对角线BD上一点且BE=BC,点P为线段CE上一动点,且PM⊥BE于M,PN⊥BC于N,则PM+PN的值为________.
类型二 正方形中利用旋转性解题
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是__________.
5.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:S△AEF=S△ABE+S△ADF.
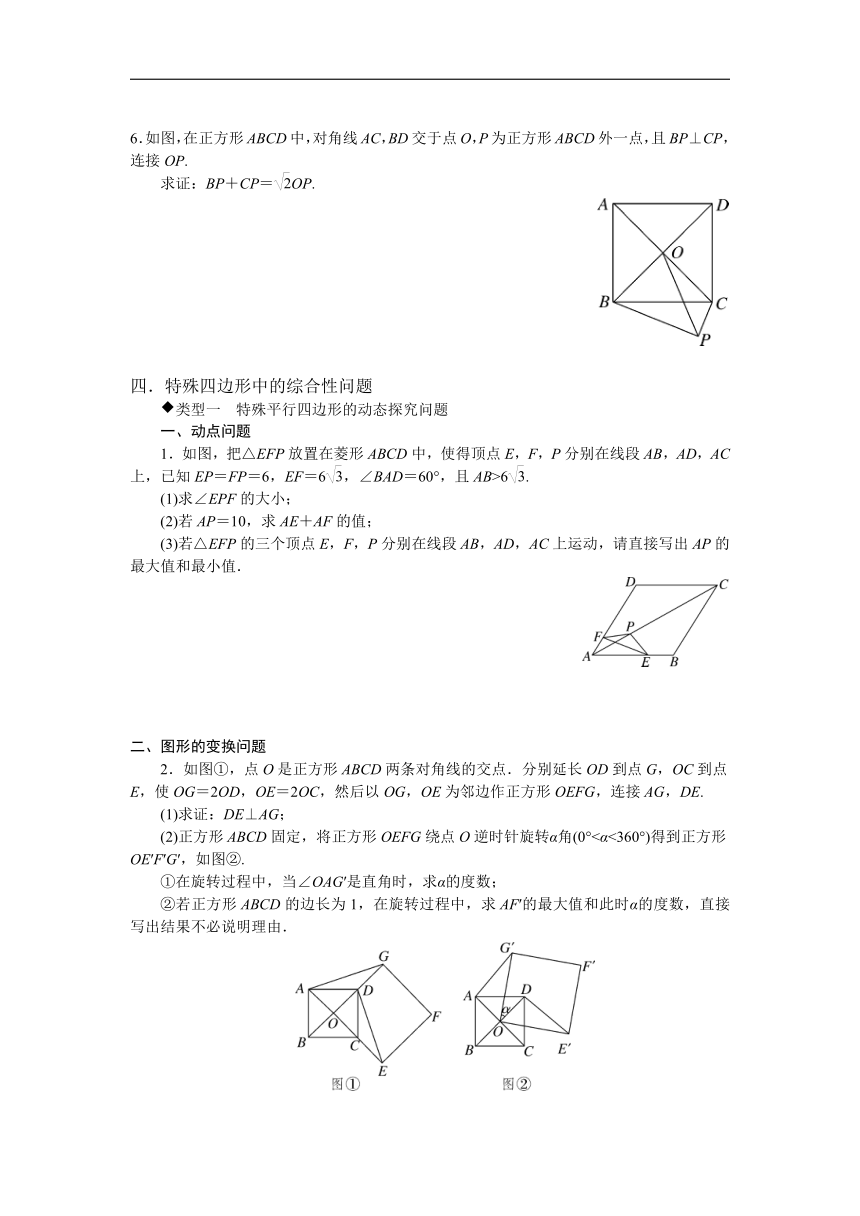
6.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP,连接OP.
求证:BP+CP=OP.
四.特殊四边形中的综合性问题
类型一 特殊平行四边形的动态探究问题
一、动点问题
1.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP的最大值和最小值.
二、图形的变换问题
2.如图①,点O是正方形ABCD两条对角线的交点.分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG,OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′的最大值和此时α的度数,直接写出结果不必说明理由.
类型二 四边形间的综合性问题
3.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
四.四边形中的探究与创新
1.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P、P′分别是EF、E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( )
A.28 B.24
C.32 D.32-8
第1题图 第2题图
2.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(______________+______________).
易知S△ADC=S△ABC,______________=______________,______________=______________.可得S矩形NFGD=S矩形EBMF.
3.如图①,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图②,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
4.邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图①, ABCD中,若AB=1,BC=2,则 ABCD为1阶准菱形.
(1)猜想与计算:邻边长分别为3和5的平行四边形是________阶准菱形;已知 ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出 ABCD是________阶准菱形;
(2)操作与推理:小明为了剪去一个菱形,进行了如下操作:如图②,把 ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.求证:四边形ABFE是菱形.
参考答案与解析
一
1.B 解析:由折叠可知∠EFC=∠EFC′=125°.∵在矩形ABCD中,AD∥BC,∴∠DEF=180°-125°=55°.根据折叠可知∠BEF=∠DEF=55°,∴∠BED=110°.∵四边形ABCD为矩形,∠A=90°,∴∠ABE=110°-90°=20°.故选B.
2.B 3.C 4.C
解析:如图,连接BF交AE于H,由折叠的性质可知BE=FE,AB=AF,∠BAE=∠FAE,∴AH⊥BF,BH=FH.∵BC=6,点E为BC的中点,∴BE=BC=3.又∵AB=4,∴在Rt△ABE中,由勾股定理得AE==5.∵S△ABE=AB·BE=AE·BH,∴BH=,则BF=2BH=.∵E是BC的中点,∴FE=BE=EC,∴∠BFC=90°.在Rt△BFC中,由勾股定理得CF===.
6.(1)证明:∵四边形ABCD是矩形,∴AB=CD,∠B=∠D=90°.∵将矩形ABCD沿对角线AC翻折,点B落在点F处,∴∠F=∠B,AB=AF,∴AF=CD,∠F=∠D.在△AFE与△CDE中,∴△AFE≌△CDE.
(2)解:∵AB=4,BC=8,∴CF=AD=8,AF=CD=AB=4.∵△AFE≌△CDE,∴EF=DE.在Rt△CED中,由勾股定理得DE2+CD2=CE2,即DE2+42=(8-DE)2,∴DE=3,∴AE=8-3=5,∴S阴影=×4×5=10.
7.解:(1)由折叠性质得△ANM≌△ADM,∴∠MAN=∠DAM.∵AN平分∠MAB,∴∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB.∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴AM=2DM.在Rt△ADM中,∵AD=3,∴由勾股定理得AM2-DM2=AD2,即(2DM)2-DM2=32,解得DM=.
(2)延长MN交AB的延长线于点Q,如图所示.∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折叠性质得△ANM≌△ADM,∴∠ANM=∠D=90°,∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ.设NQ=x,则AQ=MQ=MN+NQ=1+x.∵∠ANM=90°,∴∠ANQ=90°.在Rt△ANQ中,由勾股定理得AQ2=AN2+NQ2,即(x+1)2=32+x2,解得x=4,∴NQ=4,AQ=5.∵△NAB和△NAQ在AB边上的高相等,AB=4,AQ=5,∴S△NAB=S△NAQ=××AN·NQ=××3×4=.
二.
1.3
2.证明:延长CB到点H,使得HB=DF,连接AH.∵四边形ABCD是正方形,∴∠ABH=∠D=90°,AB=AD.∴△ADF绕点A顺时针旋转90°后能和△ABH重合.∴AH=AF,∠BAH=∠DAF.∵∠HAE=∠HAB+∠BAE=∠DAF+∠BAE=90°-∠EAF=90°-45°=45°,∴∠HAE=∠EAF=45°.又∵AE=AE,∴△AEF与△AEH关于直线AE对称,∴S△AEF=S△AEH=S△ABE+S△ABH=S△ABE+S△ADF.
3.证明:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°.将△OCP顺时针旋转90°至△OBE(如图所示),∴OE=OP,BE=CP,∠OBE=∠OCP,∠BOE=∠COP.∵BP⊥CP,∴∠BPC=90°.∵∠BOC+∠OBP+∠BPC+∠OCP=360°,∴∠OBP+∠OCP=180°,∴∠OBP+∠OBE=180°,∴E,B,P在同一直线上.∵∠POC+∠POB=∠BOC=90°,∠BOE=∠COP,∴∠BOE+∠POB=90°,即∠EOP=90°.在Rt△EOP中,由勾股定理得PE===OP.∵PE=BE+BP,BE=CP,∴BP+CP=OP.
4.B 解析:连接PB.∵点P在正方形ABCD的对角线AC上,∴PD=PB,∴PD+PE的最小值就是PB+PE的最小值,∴PD+PE的最小值就是BE.∵△ABE是等边三角形,∴BE=AB.∵S正方形ABCD=12,∴BE2=AB2=12,即BE=2,故选B.
5.
6.证明:∵B,D关于AC对称,点F在AC上,∴BF=DF.∵四边形ABCD是正方形,∴AD=BC,∠ADE=∠BCE.∵点E是CD的中点,∴DE=CE.在△ADE和△BCE中,∵AD=BC,∠ADE=∠BCE,DE=CE,∴△ADE≌△BCE,∴AE=BE,∴∠BAE=∠ABE.∵MF∥AE,∴∠BAE=∠BMF,∴∠BMF=∠ABE,∴MF=BF.∵BF=DF,∴DF=MF.
三.
解析:如图,过点Q作QE⊥AC交AB于点E,则PQ=PE.∴DP+PQ=DP+PE.当点D,P,E三点共线的时候DP+PQ=DP+PE=DE最小,且DE即为所求.当DE⊥AB时,DE最小.∵四边形ABCD是菱形,∴AC⊥BD,OA=AC=4,OB=BD=3,∴AB=5.∵S菱形ABCD=AC·BD=AB·DE,∴×8×6=5·DE,∴DE=.∴DP+PQ的最小值为.
2.6 解析:如图,设BE与AC交于点P,连接BD.∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE,即P为AC与BE的交点时,PD+PE最小,为BE的长度.∵正方形ABCD的边长为6,∴AB=6.又∵△ABE是等边三角形,∴BE=AB=6.故所求最小值为6.故答案为6.
解析:∵四边形ABCD为矩形,∴∠ABC=90°.∵AB=6,BC=8,∴AC=10,∴OB=OC=AC=5.如图,连接OP,∵S△OBP+S△OCP=S△OBC,∴+=S△OBC,∴+=S△OBC.∵S△OBC=S矩形ABCD=AB·BC=×6×8=12,∴+=12,∴PE+PF=.
【变式题】(1) 解析:∵菱形ABCD的周长为40,面积为25,∴AB=AD=10,S△ABD=.连接AP,则S△ABD=S△ABP+S△ADP,∴×10(PE+PF)=,∴PE+PF=.
(2) 解析:连接BP,过点E作EH⊥BC于H.∵S△BPE+S△BPC=S△BEC,∴+=.又∵BE=BC,∴+=,即PM+PN=EH.∵△BEH为等腰直角三角形,且BE=BC=1,∴EH=,∴PM+PN=EH=.
4.3
5.证明:延长CB到点H,使得HB=DF,连接AH.∵四边形ABCD是正方形,∴∠ABH=∠D=90°,AB=AD.∴△ADF绕点A顺时针旋转90°后能和△ABH重合,∴AH=AF,∠BAH=∠DAF.∵∠HAE=∠HAB+∠BAE=∠DAF+∠BAE=90°-∠EAF=90°-45°=45°,∴∠HAE=∠EAF=45°.又∵AE=AE,∴△AEF与△AEH关于直线AE对称,∴S△AEF=S△AEH=S△ABE+S△ABH=S△ABE+S△ADF.
6.证明:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°.将△OCP顺时针旋转90°至△OBE(如图所示),∴OE=OP,BE=CP,∠OBE=∠OCP,∠BOE=∠COP.∵BP⊥CP,∴∠BPC=90°.∵∠BOC+∠OBP+∠BPC+∠OCP=360°,∴∠OBP+∠OCP=180°,∴∠OBP+∠OBE=180°,∴E,B,P在同一直线上.∵∠POC+∠POB=∠BOC=90°,∠BOE=∠COP,∴∠BOE+∠POB=90°,即∠EOP=90°.在Rt△EOP中,由勾股定理得PE===OP.∵PE=BE+BP,BE=CP,∴BP+CP=OP.
四.
1.解:(1)如图①,过点P作PG⊥EF于点G,H为PE的中点,连接GH,∴∠PGE=90°,GH=PH=HE=PE=3.∵PF=PE,∴∠FPG=∠EPG,FG=GE=EF=3.在Rt△PGE中,由勾股定理得PG===3.∴PG=GH=PH,即△GPH为等边三角形,∴∠GPH=60°,∴∠FPE=∠FPG+∠GPE=2∠GPE=2×60°=120°.
(2)如图①,过点P作PM⊥AB于点M,作PN⊥AD于点N,∴∠ANP=∠AMP=90°.∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC=∠DAB=30°,PM=PN.在Rt△PME和Rt△PNF中,PM=PN,PE=PF,∴Rt△PME≌Rt△PNF,∴ME=NF.∵∠PAM=30°,AP=10,∴PM=AP=5.由勾股定理得AM==5.在△ANP和△AMP中,∴△ANP≌△AMP,∴AN=AM=5.∴AE+AF=(AM+ME)+(AN-NF)=AM+AN+ME-NF=10.
(3)如图②,△EFP的三个顶点分别在AB,AD,AC上运动,点P在P1,P之间运动.P1O=PO=PE=3,AE=EF=6,AO==9.∴AP的最大值为AO+OP=12,AP的最小值为AO-OP1=6.
2.(1)证明:如图,延长ED交AG于点H.∵四边形ABCD与OEFG均为正方形,∴OA=OD,OG=OE,∠AOG=∠DOE=90°,∴Rt△AOG≌Rt△DOE,∴∠AGO=∠DEO.∵∠AGO+∠GAO=90°,∴∠DEO+∠GAO=90°,∴∠AHE=90°,即DE⊥AG;
(2)解:①在旋转过程中,∠OAG′成为直角有以下两种情况:
a.α由0°增大到90°过程中,当∠OAG′为直角时,∵OA=OD=OG=OG′,∴∠AG′O=30°,∠AOG′=60°.∵OA⊥OD,∴∠DOG′=90°-∠AOG′=30°,即α=30°;
b.α由90°增大到180°过程中,当∠OAG′为直角时,同理可求的∠AOG′=60°,∴α=90°+∠AOG′=150°.综上,当∠OAG′为直角时,α=30°或150°;
②AF′长的最大值是2+,此时α=315°.
3.(1)证明:如图①中,连接BD.∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD.∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形.
(2)解:四边形EFGH是菱形.理由如下:如图②中,连接AC,BD.∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD.在△APC和△BPD中,∴△APC≌△BPD,∴AC=BD.∵点E,F,G分别为边AB,BC,CD的中点,∴EF=AC,FG=BD,∴EF=FG.∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.
(3)解:四边形EFGH是正方形.理由如下:如图②中,设AC与BD交于点O.AC与PD交于点M,AC与EH交于点N.∵△APC≌△BPD,∴∠ACP=∠BDP.∵∠DMO=∠CMP,∴∠COD=∠CPD=90°.∵EH∥BD,AC∥HG,∴∠EHG=∠ENO=∠BOC=∠DOC=90°.∵四边形EFGH是菱形,∴四边形EFGH是正方形.
一 :折叠中的方程思想及数形结合思想
类型一 折叠中求角度
1.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF.若∠EFC′=125°,那么∠ABE的度数为( )
A.15° B.20° C.25° D.30°
第1题图 第2题图
2.如图,某数学兴趣小组开展以下折纸活动:(1)对折矩形纸片ABCD,使AD和BC重合,得到折痕EF,把纸片展平;(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN.观察探究可以得到∠ABM的度数是( )
A.25° B.30° C.36° D.45°
类型二 折叠中求线段长
3.如图,在矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.6cm B.7cm C.8cm D.9cm
第3题图 第4题图
4.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )
A.3 B. C.5 D.
5.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内的点F处,连接CF,则CF的长为________.
类型三 折叠中求面积
6.如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
7.如图,矩形ABCD中,AB=4,AD=3,M是边CD上的一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积.
二.正方形中的最值及旋转变化模型问题
类型一 利用正方形的旋转性质解题
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P,若四边形ABCD的面积是18,则DP的长是__________.
2.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.
求证:S△AEF=S△ABE+S△ADF.
3.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP.
求证:BP+CP=OP.
类型二 利用正方形的对称性解题
4.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. B.2 C.2 D.
第4题图 第5题图
5.如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为________.
6.如图,在正方形ABCD中,点E是CD的中点,AC,BE交于点F,MF∥AE交AB于M.
求证:DF=MF.
三.特殊平行四边形中的解题方法
类型一 特殊四边形中求最值、定值问题
一、利用对称性求最值【方法10】
1.如图,四边形ABCD是菱形,AC=8,DB=6,P,Q分别是AC,AD上的动点,连接DP,PQ,则DP+PQ的最小值为________.
第1题图 第2题图
2.如图,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.
二、利用面积法求定值
如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,AB=6,BC=8,则PE+PF的值为________.
【变式题】矩形两条垂线段之和→菱形两条垂线段之和→正方形两条垂线段之和
(1)如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于________.
变式题(1)图 变式题(2)图
(2)如图,正方形ABCD的边长为1,E为对角线BD上一点且BE=BC,点P为线段CE上一动点,且PM⊥BE于M,PN⊥BC于N,则PM+PN的值为________.
类型二 正方形中利用旋转性解题
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是__________.
5.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:S△AEF=S△ABE+S△ADF.
6.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP,连接OP.
求证:BP+CP=OP.
四.特殊四边形中的综合性问题
类型一 特殊平行四边形的动态探究问题
一、动点问题
1.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP的最大值和最小值.
二、图形的变换问题
2.如图①,点O是正方形ABCD两条对角线的交点.分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG,OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′的最大值和此时α的度数,直接写出结果不必说明理由.
类型二 四边形间的综合性问题
3.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
四.四边形中的探究与创新
1.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P、P′分别是EF、E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( )
A.28 B.24
C.32 D.32-8
第1题图 第2题图
2.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(______________+______________).
易知S△ADC=S△ABC,______________=______________,______________=______________.可得S矩形NFGD=S矩形EBMF.
3.如图①,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图②,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
4.邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图①, ABCD中,若AB=1,BC=2,则 ABCD为1阶准菱形.
(1)猜想与计算:邻边长分别为3和5的平行四边形是________阶准菱形;已知 ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出 ABCD是________阶准菱形;
(2)操作与推理:小明为了剪去一个菱形,进行了如下操作:如图②,把 ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.求证:四边形ABFE是菱形.
参考答案与解析
一
1.B 解析:由折叠可知∠EFC=∠EFC′=125°.∵在矩形ABCD中,AD∥BC,∴∠DEF=180°-125°=55°.根据折叠可知∠BEF=∠DEF=55°,∴∠BED=110°.∵四边形ABCD为矩形,∠A=90°,∴∠ABE=110°-90°=20°.故选B.
2.B 3.C 4.C
解析:如图,连接BF交AE于H,由折叠的性质可知BE=FE,AB=AF,∠BAE=∠FAE,∴AH⊥BF,BH=FH.∵BC=6,点E为BC的中点,∴BE=BC=3.又∵AB=4,∴在Rt△ABE中,由勾股定理得AE==5.∵S△ABE=AB·BE=AE·BH,∴BH=,则BF=2BH=.∵E是BC的中点,∴FE=BE=EC,∴∠BFC=90°.在Rt△BFC中,由勾股定理得CF===.
6.(1)证明:∵四边形ABCD是矩形,∴AB=CD,∠B=∠D=90°.∵将矩形ABCD沿对角线AC翻折,点B落在点F处,∴∠F=∠B,AB=AF,∴AF=CD,∠F=∠D.在△AFE与△CDE中,∴△AFE≌△CDE.
(2)解:∵AB=4,BC=8,∴CF=AD=8,AF=CD=AB=4.∵△AFE≌△CDE,∴EF=DE.在Rt△CED中,由勾股定理得DE2+CD2=CE2,即DE2+42=(8-DE)2,∴DE=3,∴AE=8-3=5,∴S阴影=×4×5=10.
7.解:(1)由折叠性质得△ANM≌△ADM,∴∠MAN=∠DAM.∵AN平分∠MAB,∴∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB.∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴AM=2DM.在Rt△ADM中,∵AD=3,∴由勾股定理得AM2-DM2=AD2,即(2DM)2-DM2=32,解得DM=.
(2)延长MN交AB的延长线于点Q,如图所示.∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折叠性质得△ANM≌△ADM,∴∠ANM=∠D=90°,∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ.设NQ=x,则AQ=MQ=MN+NQ=1+x.∵∠ANM=90°,∴∠ANQ=90°.在Rt△ANQ中,由勾股定理得AQ2=AN2+NQ2,即(x+1)2=32+x2,解得x=4,∴NQ=4,AQ=5.∵△NAB和△NAQ在AB边上的高相等,AB=4,AQ=5,∴S△NAB=S△NAQ=××AN·NQ=××3×4=.
二.
1.3
2.证明:延长CB到点H,使得HB=DF,连接AH.∵四边形ABCD是正方形,∴∠ABH=∠D=90°,AB=AD.∴△ADF绕点A顺时针旋转90°后能和△ABH重合.∴AH=AF,∠BAH=∠DAF.∵∠HAE=∠HAB+∠BAE=∠DAF+∠BAE=90°-∠EAF=90°-45°=45°,∴∠HAE=∠EAF=45°.又∵AE=AE,∴△AEF与△AEH关于直线AE对称,∴S△AEF=S△AEH=S△ABE+S△ABH=S△ABE+S△ADF.
3.证明:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°.将△OCP顺时针旋转90°至△OBE(如图所示),∴OE=OP,BE=CP,∠OBE=∠OCP,∠BOE=∠COP.∵BP⊥CP,∴∠BPC=90°.∵∠BOC+∠OBP+∠BPC+∠OCP=360°,∴∠OBP+∠OCP=180°,∴∠OBP+∠OBE=180°,∴E,B,P在同一直线上.∵∠POC+∠POB=∠BOC=90°,∠BOE=∠COP,∴∠BOE+∠POB=90°,即∠EOP=90°.在Rt△EOP中,由勾股定理得PE===OP.∵PE=BE+BP,BE=CP,∴BP+CP=OP.
4.B 解析:连接PB.∵点P在正方形ABCD的对角线AC上,∴PD=PB,∴PD+PE的最小值就是PB+PE的最小值,∴PD+PE的最小值就是BE.∵△ABE是等边三角形,∴BE=AB.∵S正方形ABCD=12,∴BE2=AB2=12,即BE=2,故选B.
5.
6.证明:∵B,D关于AC对称,点F在AC上,∴BF=DF.∵四边形ABCD是正方形,∴AD=BC,∠ADE=∠BCE.∵点E是CD的中点,∴DE=CE.在△ADE和△BCE中,∵AD=BC,∠ADE=∠BCE,DE=CE,∴△ADE≌△BCE,∴AE=BE,∴∠BAE=∠ABE.∵MF∥AE,∴∠BAE=∠BMF,∴∠BMF=∠ABE,∴MF=BF.∵BF=DF,∴DF=MF.
三.
解析:如图,过点Q作QE⊥AC交AB于点E,则PQ=PE.∴DP+PQ=DP+PE.当点D,P,E三点共线的时候DP+PQ=DP+PE=DE最小,且DE即为所求.当DE⊥AB时,DE最小.∵四边形ABCD是菱形,∴AC⊥BD,OA=AC=4,OB=BD=3,∴AB=5.∵S菱形ABCD=AC·BD=AB·DE,∴×8×6=5·DE,∴DE=.∴DP+PQ的最小值为.
2.6 解析:如图,设BE与AC交于点P,连接BD.∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE,即P为AC与BE的交点时,PD+PE最小,为BE的长度.∵正方形ABCD的边长为6,∴AB=6.又∵△ABE是等边三角形,∴BE=AB=6.故所求最小值为6.故答案为6.
解析:∵四边形ABCD为矩形,∴∠ABC=90°.∵AB=6,BC=8,∴AC=10,∴OB=OC=AC=5.如图,连接OP,∵S△OBP+S△OCP=S△OBC,∴+=S△OBC,∴+=S△OBC.∵S△OBC=S矩形ABCD=AB·BC=×6×8=12,∴+=12,∴PE+PF=.
【变式题】(1) 解析:∵菱形ABCD的周长为40,面积为25,∴AB=AD=10,S△ABD=.连接AP,则S△ABD=S△ABP+S△ADP,∴×10(PE+PF)=,∴PE+PF=.
(2) 解析:连接BP,过点E作EH⊥BC于H.∵S△BPE+S△BPC=S△BEC,∴+=.又∵BE=BC,∴+=,即PM+PN=EH.∵△BEH为等腰直角三角形,且BE=BC=1,∴EH=,∴PM+PN=EH=.
4.3
5.证明:延长CB到点H,使得HB=DF,连接AH.∵四边形ABCD是正方形,∴∠ABH=∠D=90°,AB=AD.∴△ADF绕点A顺时针旋转90°后能和△ABH重合,∴AH=AF,∠BAH=∠DAF.∵∠HAE=∠HAB+∠BAE=∠DAF+∠BAE=90°-∠EAF=90°-45°=45°,∴∠HAE=∠EAF=45°.又∵AE=AE,∴△AEF与△AEH关于直线AE对称,∴S△AEF=S△AEH=S△ABE+S△ABH=S△ABE+S△ADF.
6.证明:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°.将△OCP顺时针旋转90°至△OBE(如图所示),∴OE=OP,BE=CP,∠OBE=∠OCP,∠BOE=∠COP.∵BP⊥CP,∴∠BPC=90°.∵∠BOC+∠OBP+∠BPC+∠OCP=360°,∴∠OBP+∠OCP=180°,∴∠OBP+∠OBE=180°,∴E,B,P在同一直线上.∵∠POC+∠POB=∠BOC=90°,∠BOE=∠COP,∴∠BOE+∠POB=90°,即∠EOP=90°.在Rt△EOP中,由勾股定理得PE===OP.∵PE=BE+BP,BE=CP,∴BP+CP=OP.
四.
1.解:(1)如图①,过点P作PG⊥EF于点G,H为PE的中点,连接GH,∴∠PGE=90°,GH=PH=HE=PE=3.∵PF=PE,∴∠FPG=∠EPG,FG=GE=EF=3.在Rt△PGE中,由勾股定理得PG===3.∴PG=GH=PH,即△GPH为等边三角形,∴∠GPH=60°,∴∠FPE=∠FPG+∠GPE=2∠GPE=2×60°=120°.
(2)如图①,过点P作PM⊥AB于点M,作PN⊥AD于点N,∴∠ANP=∠AMP=90°.∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC=∠DAB=30°,PM=PN.在Rt△PME和Rt△PNF中,PM=PN,PE=PF,∴Rt△PME≌Rt△PNF,∴ME=NF.∵∠PAM=30°,AP=10,∴PM=AP=5.由勾股定理得AM==5.在△ANP和△AMP中,∴△ANP≌△AMP,∴AN=AM=5.∴AE+AF=(AM+ME)+(AN-NF)=AM+AN+ME-NF=10.
(3)如图②,△EFP的三个顶点分别在AB,AD,AC上运动,点P在P1,P之间运动.P1O=PO=PE=3,AE=EF=6,AO==9.∴AP的最大值为AO+OP=12,AP的最小值为AO-OP1=6.
2.(1)证明:如图,延长ED交AG于点H.∵四边形ABCD与OEFG均为正方形,∴OA=OD,OG=OE,∠AOG=∠DOE=90°,∴Rt△AOG≌Rt△DOE,∴∠AGO=∠DEO.∵∠AGO+∠GAO=90°,∴∠DEO+∠GAO=90°,∴∠AHE=90°,即DE⊥AG;
(2)解:①在旋转过程中,∠OAG′成为直角有以下两种情况:
a.α由0°增大到90°过程中,当∠OAG′为直角时,∵OA=OD=OG=OG′,∴∠AG′O=30°,∠AOG′=60°.∵OA⊥OD,∴∠DOG′=90°-∠AOG′=30°,即α=30°;
b.α由90°增大到180°过程中,当∠OAG′为直角时,同理可求的∠AOG′=60°,∴α=90°+∠AOG′=150°.综上,当∠OAG′为直角时,α=30°或150°;
②AF′长的最大值是2+,此时α=315°.
3.(1)证明:如图①中,连接BD.∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD.∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形.
(2)解:四边形EFGH是菱形.理由如下:如图②中,连接AC,BD.∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD.在△APC和△BPD中,∴△APC≌△BPD,∴AC=BD.∵点E,F,G分别为边AB,BC,CD的中点,∴EF=AC,FG=BD,∴EF=FG.∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.
(3)解:四边形EFGH是正方形.理由如下:如图②中,设AC与BD交于点O.AC与PD交于点M,AC与EH交于点N.∵△APC≌△BPD,∴∠ACP=∠BDP.∵∠DMO=∠CMP,∴∠COD=∠CPD=90°.∵EH∥BD,AC∥HG,∴∠EHG=∠ENO=∠BOC=∠DOC=90°.∵四边形EFGH是菱形,∴四边形EFGH是正方形.
