人教版八年级下册18.1.1平行四边形的性质课后练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.1.1平行四边形的性质课后练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 586.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 10:35:45 | ||
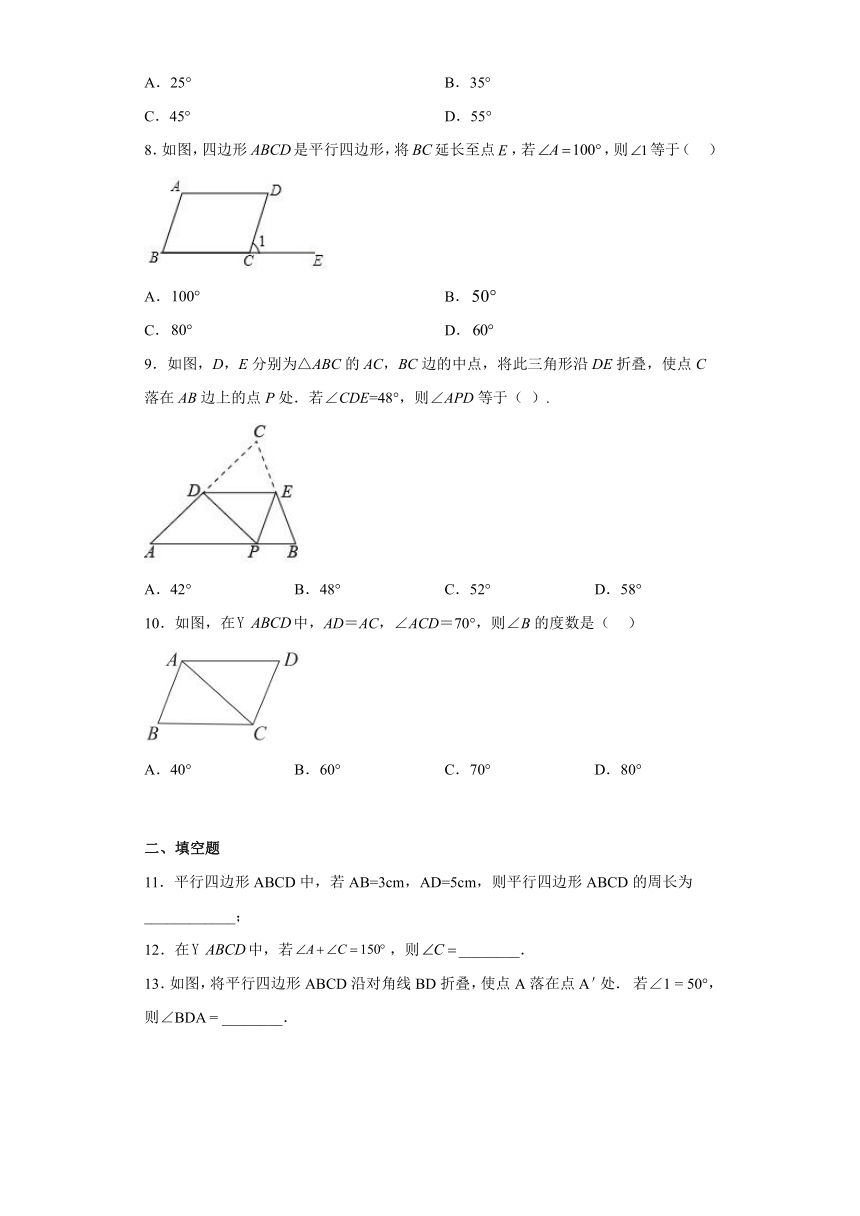
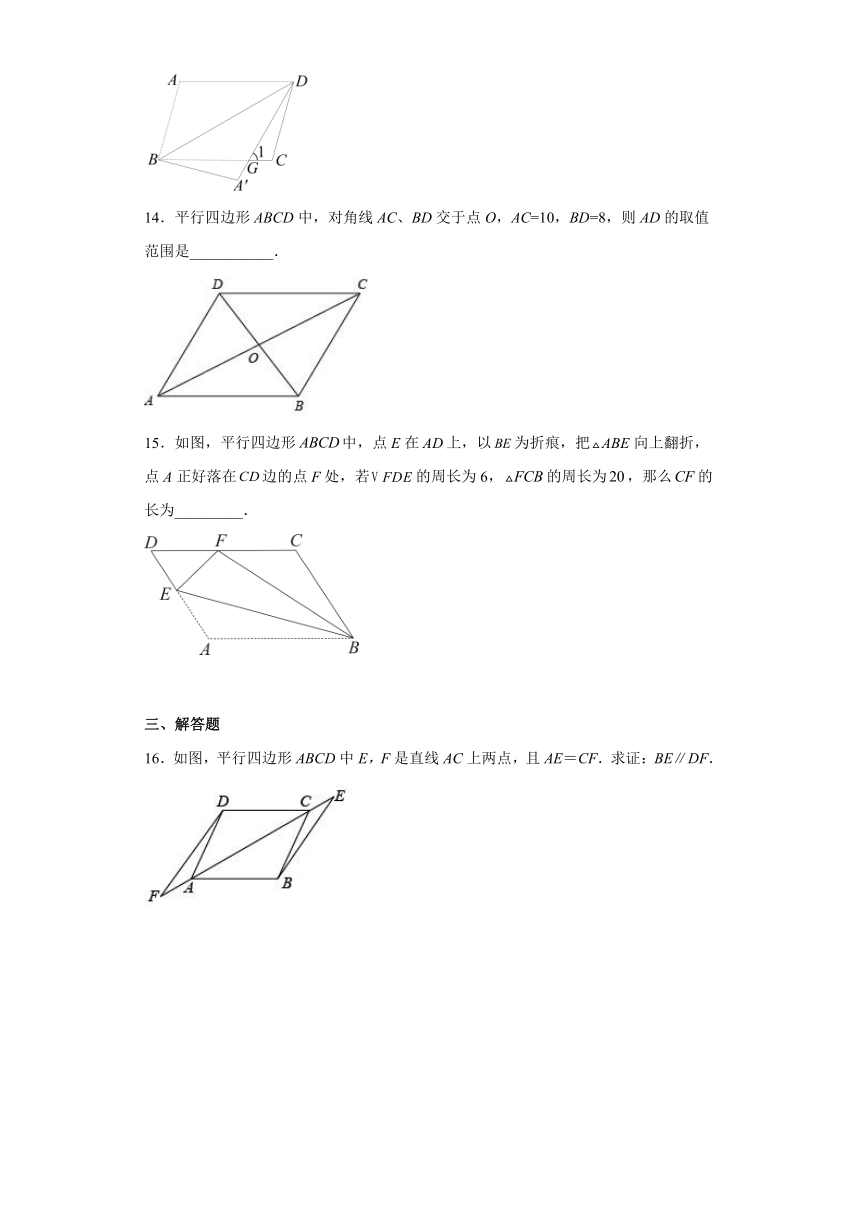
图片预览



文档简介
18.1.1平行四边形的性质 课后练习
一、单选题
1.平行四边形ABCD中,若比小40°,则的度数为( ).
A.60° B.70° C.80° D.110°
2.如图,在□ABCD中,下列结论不一定成立的是( )
A.∠1=∠2 B.AD=DC C.∠ADC=∠CBA D.OA=OC
3.在平行四边形ABCD中,,则的大小是( )
A. B. C. D.
4.在平行四边形ABCD中,若∠A∶∠B=5∶4,则∠C的度数为( )
A.80° B.120° C.100° D.110°
5.如图,在中,,则的大小是( )
A. B. C. D.
6.如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若,则的周长为( )
A.24 B.22 C.16 D.12
7.如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE 的角度为( )
A.25° B.35°
C.45° D.55°
8.如图,四边形是平行四边形,将延长至点,若,则等于( )
A. B.
C. D.
9.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( ).
A.42° B.48° C.52° D.58°
10.如图,在中,AD=AC,∠ACD=70°,则∠B的度数是( )
A.40° B.60° C.70° D.80°
二、填空题
11.平行四边形ABCD中,若AB=3cm,AD=5cm,则平行四边形ABCD的周长为 ____________;
12.在中,若,则________.
13.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处. 若∠1 = 50°,则∠BDA = ________.
14.平行四边形ABCD中,对角线AC、BD交于点O,AC=10,BD=8,则AD的取值范围是___________.
15.如图,平行四边形中,点E在上,以为折痕,把向上翻折,点A正好落在边的点F处,若的周长为6,的周长为,那么的长为_________.
三、解答题
16.如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.求证:BE∥DF.
17.如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,求△BOC的周长为多大?
18.如图,在中,点是边上的一个动点(点不与、两点重合),过点作直线,直线与的平分线相交于点,与(的外角)的平分线相交于点.
(1)与相等吗?为什么?
(2)探究:当点运动到何处时,四边形是矩形?并证明你的结论.
(3)在(2)中当等于多少时,四边形为正方形(不要求说理由)
19.如图,已知在中,对角线交于点分别在线段上,且,连结.
(1)求证:;
(2)若,求直线与之间的距离.
20.在平行四边形ABCD中,用尺规作图的角平分线(不用写过程,留下作图痕迹),交DC边于点H,若,,求平行四边形ABCD的周长.
参考答案
1.B
2.B
3.B
4.C
5.B
6.A
7.B
8.C
9.B
10.C
11.16cm
12.75
13.25
14.115.7
16.证:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD ,
∴∠ACD=∠CAB.
∵CF=AE,
∴△CFD≌△AEB(SAS),
∴∠F=∠E,
∴BE∥DF.
17.解:∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14.
18.(1),理由如下:
∵根据题意,有平分,平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴;
(2)是中点时,四边形是矩形,理由如下:
在(1)已证明,
∵是中点,
∴,
∴,
∴,且、互相平分,
∴四边形是矩形;
(3)当时,四边形为正方形,理由如下:
在(2)中已证明四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴矩形是正方形.
19.解:(1)∵四边形是平行四边形,
∴OC=OA,
∴在和中,
∴△EOC≌△FOA(SAS).
∴CE=AF.
(2)如图所示,作AH⊥BC交BC于点H,可得AH的长度即直线与之间的距离.
∵,
∴是等腰直角三角形,
∴,
∴AC=2OA=2.
∴在Rt△ABC中,,
∴在Rt△ABC中,
由题意可知:,
即,
解得:.
∴直线与之间的距离为.
20.如图,BH为所作.
∵BH平分∠ABC,
∴∠ABH=∠CBH,
∵四边形ABCD为平行四边形,
∴CD∥AB,AB=CD,AD=BC=6,
∴∠ABH=∠BHC,
∴∠CBH=∠BHC,
∴CH=BC=6,
∵DH=CH,
∴DH=3,
∴平行四边形ABCD的周长=2(BC+CD)=2×(6+9)=30.
一、单选题
1.平行四边形ABCD中,若比小40°,则的度数为( ).
A.60° B.70° C.80° D.110°
2.如图,在□ABCD中,下列结论不一定成立的是( )
A.∠1=∠2 B.AD=DC C.∠ADC=∠CBA D.OA=OC
3.在平行四边形ABCD中,,则的大小是( )
A. B. C. D.
4.在平行四边形ABCD中,若∠A∶∠B=5∶4,则∠C的度数为( )
A.80° B.120° C.100° D.110°
5.如图,在中,,则的大小是( )
A. B. C. D.
6.如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若,则的周长为( )
A.24 B.22 C.16 D.12
7.如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE 的角度为( )
A.25° B.35°
C.45° D.55°
8.如图,四边形是平行四边形,将延长至点,若,则等于( )
A. B.
C. D.
9.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( ).
A.42° B.48° C.52° D.58°
10.如图,在中,AD=AC,∠ACD=70°,则∠B的度数是( )
A.40° B.60° C.70° D.80°
二、填空题
11.平行四边形ABCD中,若AB=3cm,AD=5cm,则平行四边形ABCD的周长为 ____________;
12.在中,若,则________.
13.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处. 若∠1 = 50°,则∠BDA = ________.
14.平行四边形ABCD中,对角线AC、BD交于点O,AC=10,BD=8,则AD的取值范围是___________.
15.如图,平行四边形中,点E在上,以为折痕,把向上翻折,点A正好落在边的点F处,若的周长为6,的周长为,那么的长为_________.
三、解答题
16.如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.求证:BE∥DF.
17.如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,求△BOC的周长为多大?
18.如图,在中,点是边上的一个动点(点不与、两点重合),过点作直线,直线与的平分线相交于点,与(的外角)的平分线相交于点.
(1)与相等吗?为什么?
(2)探究:当点运动到何处时,四边形是矩形?并证明你的结论.
(3)在(2)中当等于多少时,四边形为正方形(不要求说理由)
19.如图,已知在中,对角线交于点分别在线段上,且,连结.
(1)求证:;
(2)若,求直线与之间的距离.
20.在平行四边形ABCD中,用尺规作图的角平分线(不用写过程,留下作图痕迹),交DC边于点H,若,,求平行四边形ABCD的周长.
参考答案
1.B
2.B
3.B
4.C
5.B
6.A
7.B
8.C
9.B
10.C
11.16cm
12.75
13.25
14.1
16.证:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD ,
∴∠ACD=∠CAB.
∵CF=AE,
∴△CFD≌△AEB(SAS),
∴∠F=∠E,
∴BE∥DF.
17.解:∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14.
18.(1),理由如下:
∵根据题意,有平分,平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴;
(2)是中点时,四边形是矩形,理由如下:
在(1)已证明,
∵是中点,
∴,
∴,
∴,且、互相平分,
∴四边形是矩形;
(3)当时,四边形为正方形,理由如下:
在(2)中已证明四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴矩形是正方形.
19.解:(1)∵四边形是平行四边形,
∴OC=OA,
∴在和中,
∴△EOC≌△FOA(SAS).
∴CE=AF.
(2)如图所示,作AH⊥BC交BC于点H,可得AH的长度即直线与之间的距离.
∵,
∴是等腰直角三角形,
∴,
∴AC=2OA=2.
∴在Rt△ABC中,,
∴在Rt△ABC中,
由题意可知:,
即,
解得:.
∴直线与之间的距离为.
20.如图,BH为所作.
∵BH平分∠ABC,
∴∠ABH=∠CBH,
∵四边形ABCD为平行四边形,
∴CD∥AB,AB=CD,AD=BC=6,
∴∠ABH=∠BHC,
∴∠CBH=∠BHC,
∴CH=BC=6,
∵DH=CH,
∴DH=3,
∴平行四边形ABCD的周长=2(BC+CD)=2×(6+9)=30.
