第四单元正比例与反比例-六年级下册数学期中重难点培优卷(北师大版)(含解析)
文档属性
| 名称 | 第四单元正比例与反比例-六年级下册数学期中重难点培优卷(北师大版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 680.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 15:16:06 | ||
图片预览




文档简介
第四单元 正比例与反比例
六年级下册数学期中重难点培优卷(北师大版)
姓名:___________班级:___________考号:___________
一、选择题
1.通过比与比例的学习,你认为下列说法不正确的是( )
A.若=3y,那么x与y成反比例
B.24:36和0.6:不能组成比例
C.在一个比例中,若两个内项互为倒数,那么它的两个外项也互为倒数
2.在①x+y=12,②y=2x,③=y,④25%∶y=x∶40中,表示x和y成反比例的式子有( )个。
A.1 B.2 C.3 D.4
3.购买鸡蛋的数量和总价成正比例关系的图像是( )。
A.B.C.
4.( )中的两种量不成比例。
A.从北京到广州,列车行驶的平均速度和所需时间
B.人的体重和身高
C.圆锥的高一定,它的体积和底面积
5.一辆汽车从甲地开往乙地,行驶的速度和时间( )
A.成正比例 B.不成比例 C.成反比例
6.表示c和a成反比例关系的式子是( )
A.c+a=0 B.ca=15 C.c=a
7.下列X和Y成反比例关系的是( )。
A.x+y=10 B.x=y C.y=(>0)
二、填空题
8.=单价(一定), 和 成 比例.
9.28÷ ==2.1:2.7= :63= 0. (填循环小数)
10.若,则=,a与b成( )比例。
11.如果=,那么X和Y成反比例. .
12.小明骑车上学的平均速度与所用时间成( )比例;分针走的圈数与时针走的圈数成( )比例。
13.甲数是乙数的,乙数与甲乙总数的比是 ,乙数比甲数多 .
14.若a×b=c,则当c一定时,________和________成反比例.
三、判断题
15.报纸的单价一定,总价与订阅的份数成反比例。 ( )
16.如果ab+5=12,那么a与b成反比例.( )
17.正方形的面积与边长成正比例。( )
18.在同一个圆中,圆的周长与直径成正比例,圆的面积与半径成反比例。( )
19.天数一定,每天烧煤量和烧煤总量成反比例。( )
20.一条路,修了的米数和未修的米数成反比例。( )
21.某汽车行驶的路程一定,行驶的速度和所需要的时间成正比例。( )
22.电的单价一定,电费和用电量成反比例。( )
四、解方程
23.解比例。
15∶x=7∶28 ∶x=0.25∶8
= ∶=x∶
五、解答题
24.学校开展勤俭节约活动,同学们3天就节约零用钱450元。照这样计算,2021年7月份同学们能节约多少零用钱?(用比例解答)
25.一列磁悬浮列车匀速行驶时,行驶的路程与时间的关系如下。
时间/分 1 2 3 4 5 …
路程/千米 7 14 21 …
(1)完成上表。
(2)在下图中画出各点,并说一说各点连线的形状。
(3)从表中可得出,路程和时间成( )比例。
(4)当列车行驶2.5分时,路程是( )千米。
26.在一间布店的柜台上,有一张写着某种花布的米数和总价如下表。
数量(米) 1 2 3 4 5 6 ……
总价(元) 9.5 19 28.5 38 47.5 57
(1)表中有________和________两种量,他们是________的量。
(2)总价怎样随着数量的而变化而变化?
27.下图是甲、乙两人出行时路程与时间的关系图。
(1)甲每时行( )km,乙每时行( )km。
(2)甲行的路程与时间成比例吗?如果成比例,成什么比例?
(3)请你结合这幅图提出一个问题,并解答。
28.印刷厂准备把一批笔记本打包,运往商店。
包数/包 1 2 3 4 5 6 7 …
本数/本 40 80 120 …
(1)把上表填完整。
(2)先根据上表描点,再在下图顺次连接各点。
(3)笔记本的包数与本数成正比例吗?
(4)点(11,440)在这条直线上吗?这一点表示什么含义?
参考答案:
1.B
【详解】试题分析:A、要判断x与y是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;
B、根据比例的意义作答,即表示两个比相等的式子叫做比例;
C、根据比例的基本性质进行判断,即在比例中,两个外项的积等于两个内项的积.
解:A、因为=3y,
所以xy=(一定),
所以x与y成反比例;
B、24:36=;
0.6:=,
所以24:36与0.6:能组成比例;故题干错误;
C、因为在比例中,两个外项的积等于两个内项的积;
又因为互为倒数的两个数的乘积是1,
所以在比例里,若两个内项互为倒数,那么它的两个外项也互为倒数;
点评:此题主要考查了反比例、比例的意义及比例的基本性质.
2.B
【分析】根据反比例的意义,如果两种相关系的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例,以此判断。
【详解】①x+y=12,是和一定,所以x和y不成反比例;
②y=2x,则=2,是比值一定,所以x和y成正比例;
③=y,则xy=7,是积一定,所以x和y成反比例;
④25%∶y=x∶40中,根据比例的基本性质得:xy=25%×40,积一定,所以x和y成反比例。
表示x和y成反比例的式子有2个。
故答案为:B
【点睛】本题考查反比例的意义,灵活运用反比例意义解答问题。
3.A
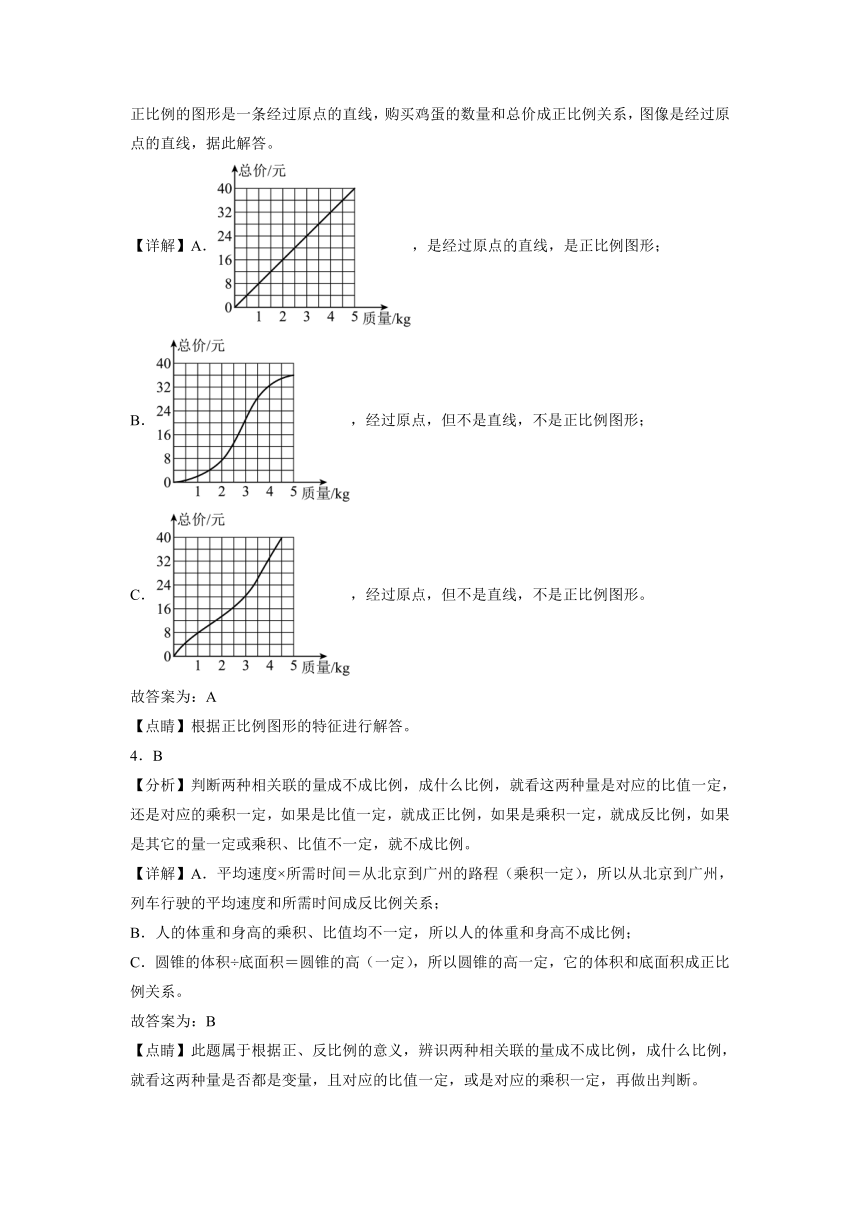
【分析】根据正比例的意义:两种相关联的量中相对的两个数的比值一定,就是正比例关系,正比例的图形是一条经过原点的直线,购买鸡蛋的数量和总价成正比例关系,图像是经过原点的直线,据此解答。
【详解】A.,是经过原点的直线,是正比例图形;
B.,经过原点,但不是直线,不是正比例图形;
C.,经过原点,但不是直线,不是正比例图形。
故答案为:A
【点睛】根据正比例图形的特征进行解答。
4.B
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.平均速度×所需时间=从北京到广州的路程(乘积一定),所以从北京到广州,列车行驶的平均速度和所需时间成反比例关系;
B.人的体重和身高的乘积、比值均不一定,所以人的体重和身高不成比例;
C.圆锥的体积÷底面积=圆锥的高(一定),所以圆锥的高一定,它的体积和底面积成正比例关系。
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
5.C
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为行驶的速度×时间=路程(一定),所以行驶的速度和时间成反比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
6.B
【详解】试题分析:依据反比例的意义,即若两个量的乘积一定,则这两个量成反比例,从而可以作出正确选择.
解:选项A,不能判断a和c的积是否一定,所以a和c不成反比例;
选项B,ca=15(一定),则c和a成反比例;
选项C,不能判断a和c的积是否一定,所以a和c不成反比例;
点评:此题主要看c和a的积是否一定,若积一定,则成反比例,否则,不成反比例.
7.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.x+y=10,是和一定,不成比例;
B.x=y,即x:y=,是比值一定,则x和y成正比例;
C.y=(>0),即xy=6,是乘积一定,则x和y成反比例。
故选:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
8.总价,数量,正.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:=单价(一定),总价和数量成正比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
9.36,7,49,0..
【详解】试题分析:解答此题的关键是2.1:2.7,根据比的基本性质化成最简整数比是7:9,根据比与分数的关系,7:9=;根据比与除法的关系,7:9=7÷9,再根据商不变的性质,被除数、除数都乘4就是28÷36;根据比的基本性质,7:9的前、后项都乘7就是49:63;7÷9=0..由此进行转化并填空.
解:28÷36==2.1:2.7=49:63=0.
点评:此题考查除式、小数、分数、比之间的转化及循环小数的求法和写法.利用它们之间的关系和性质进行转化即可.
10. 正
【详解】略
11.√.
【详解】试题分析:分数形式的比例,分子、分母交叉相乘,积相等,改写成两数相乘的等式后,再根据正、反比例的意义,即可得答案.
解:=,
X×Y=5×9=45,
所以X和Y成反比例;
点评:此题主要考查正、反比例的意义及比例的基本性质.
12. 反 正
【详解】略
13.7:12,.
【详解】试题分析:根据甲数是乙数的57,可知甲乙两数的比是,5:7,可以把甲看作5,乙数看作7,再根据比的意义和分数除法的意义求解即可.
解:(1)由题意可知,甲乙两数的比是5:7,可以把甲看作5,乙数看作7,那么甲乙总数就是5+7=12,
则乙数与甲乙总数的比就是:7:12.
(2)甲乙两数的差是7﹣5=2,根据分数除法的意义可知,2÷5=.
点评:根据题意,知道甲乙两数的比是多少,可以把甲、乙看作一个具体的数,然后再根据比的意义和分数除法的意义就可以求出结果.
14. a b
【详解】略
15.╳
【分析】根据反比例的基本意义,成反比例的两个量乘积一定,据此判断即可。
【详解】单价=总价÷订阅的份数,比值一定,总价与订阅的份数成正比例而不是反比例。
故答案为:╳
【点睛】判断两个量成正比例还是反比例,根据比例的意义,首先找准不变量,再看两个变量是乘积一定还是比值一定,乘积一定的是反比例,比值一定的是正比例。
16.√
【详解】略
17.×
【分析】正反比例判断方法是:两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,它们的关系叫做正比例关系;如果两个量的积一定,它们的关系叫做反比例关系。
【详解】正方形面积=边长×边长;所以正方形面积÷边长=边长;因为正方形面积和边长都是变化的量,正方形面积与边长的比值不能确定,所以正方形面积与边长不成正比例关系。
故答案为:×
【点睛】根据正比例意义和辨别,以及正方形面积公式进行解答。
18.×
【分析】根据圆的周长公式C=πd可知:C÷d=π(一定),所以圆的周长与它的直径成正比例关系;
根据圆的面积公式S=πr2,S÷r2=π(一定),比值一定,所以圆的面积和半径的平方成正比例,而圆的面积与半径不成比例。
【详解】在同一个圆中,圆的周长与直径成正比例,圆的面积与半径不成比例。原题说法错误。
故答案为:×
【点睛】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
19.×
【详解】天数一定,每天烧煤量和烧煤总量成正比例。故原题干说法错误。
20.×
【分析】判断修了的米数和未修的米数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例。据此进行判断。
【详解】修了的米数+未修的米数=一条路的总米数(一定),是和一定,不是乘积一定,所以修了的米数和未修的米数不成反比例。
【点睛】此题属于辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断。
21.×
【分析】根据关系式路程=速度×时间判断即可。
【详解】路程=速度×时间,汽车行驶的路程一定,即速度与时间的乘积一定,所以行驶的速度和所需要的时间成反比例;原题说法错误。
故答案为:×
【点睛】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
22.×
【分析】两个相关联的量,若它们的比值一定,则它们成正比例关系;若它们的乘积一定,则它们成反比例关系;据此分析即可。
【详解】电费÷用电量=电的单价(一定),所以电的单价一定,电费和用电量成正比例。
故答案为:×
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
23.x=60;x=24;x=25;x=
【详解】略
24.4650元
【分析】根据题意可知,同学们每天节约的零用钱是一定的,7月份一共31天,列比例解答即可。
【详解】解:设7月份同学们能节约x元零用钱。
450∶3=x∶31
3x=13950
x=4650
答:2021年7月份同学们能节约4650元零用钱。
【点睛】此题考查了列比例解决实际问题,明确变化的两个量是比值一定还是乘积一定是解题关键。
25.(1)28;35
(2)各点在一条直线上
作图见详解
(3)正
(4)17.5
【分析】(1)通过读表可知:1分钟行驶了7千米;2分钟行驶了14千米,3分钟行驶了21千米,时间每增加1分钟路程就增加7千米,时间增加几倍路程就增加几倍。
(2)横轴表示时间,纵轴表示路程,根据统计表中的数据完成统计图。
(3)由图意可知,7∶1=7,14∶2=7,21∶3=7,28∶4=7……,速度是一定的,路程和时间的比值一定,路程÷时间=速度(一定),则路程与时间成正比例关系。
(4)根据:速度×时间=路程计算。
【详解】(1)21+7=28,28+7=35
时间/分 1 2 3 4 5 …
路程/千米 7 14 21 28 35 …
(2)如图:各点在一条直线上。
(3)从表中可得出,7∶1=7,14∶2=7,21∶3=7,28∶4=7……,路程÷时间=速度(一定),路程和时间成正比例。
(4)2.5×7=17.5(千米)
【点睛】此题属于辨识成正比例的量,就看这两个量对应的比值是否一定,以及正比例的图像。
26. 花布的米数 花布的总价 相关联 总价随着数量的增加而增加.
【详解】略
27.(1)12 24 (2)成比例,成正比例。
(3)甲、乙两人谁的速度更快? 乙的速度更快。(答案不唯一)
【解析】略
28.(1)见详解
(2)见详解
(3)成正比例
(4)在这条直线上;这一点表示11包有440本笔记本
【分析】(1)根据图中的信息可知,一包是40本,可以计算出表中的数据,再填表即可;
(2)根据画折线统计图的方法,找出各点的位置,再连线即可;
(3)判断两个相关的量成什么比例,就看这两个量对应的是比值一定,还是乘积一定,如果是比值一定,则成正比例;如果乘积一定,则成反比例,据此解答;
(4)根据横轴上代表的是包数,纵轴上代表的是本数,用本数除以包数,每一包的数一致,即在这条直线上,再根据统计图的信息解答即可。
【详解】(1)40×4=160(本)
40×5=200(本)
40×6=240(本)
40×7=280(本)
包数/包 1 2 3 4 5 6 7 …
本数/本 40 80 120 160 200 2400 280 …
(2)
(3)40÷1=40(本)
80÷2=40(本)
120÷3=40(本)
……
总本书÷书的包数=每包书中的本数(一定),书的包数与总本书×正比例。
(4)440÷11=40(本)
点(11,440)在这条直线上,这一点表示11包有440本笔记本。
【点睛】本题考查正比例意义和辨识,反比例意义和辨识;以及正比例的应用。
六年级下册数学期中重难点培优卷(北师大版)
姓名:___________班级:___________考号:___________
一、选择题
1.通过比与比例的学习,你认为下列说法不正确的是( )
A.若=3y,那么x与y成反比例
B.24:36和0.6:不能组成比例
C.在一个比例中,若两个内项互为倒数,那么它的两个外项也互为倒数
2.在①x+y=12,②y=2x,③=y,④25%∶y=x∶40中,表示x和y成反比例的式子有( )个。
A.1 B.2 C.3 D.4
3.购买鸡蛋的数量和总价成正比例关系的图像是( )。
A.B.C.
4.( )中的两种量不成比例。
A.从北京到广州,列车行驶的平均速度和所需时间
B.人的体重和身高
C.圆锥的高一定,它的体积和底面积
5.一辆汽车从甲地开往乙地,行驶的速度和时间( )
A.成正比例 B.不成比例 C.成反比例
6.表示c和a成反比例关系的式子是( )
A.c+a=0 B.ca=15 C.c=a
7.下列X和Y成反比例关系的是( )。
A.x+y=10 B.x=y C.y=(>0)
二、填空题
8.=单价(一定), 和 成 比例.
9.28÷ ==2.1:2.7= :63= 0. (填循环小数)
10.若,则=,a与b成( )比例。
11.如果=,那么X和Y成反比例. .
12.小明骑车上学的平均速度与所用时间成( )比例;分针走的圈数与时针走的圈数成( )比例。
13.甲数是乙数的,乙数与甲乙总数的比是 ,乙数比甲数多 .
14.若a×b=c,则当c一定时,________和________成反比例.
三、判断题
15.报纸的单价一定,总价与订阅的份数成反比例。 ( )
16.如果ab+5=12,那么a与b成反比例.( )
17.正方形的面积与边长成正比例。( )
18.在同一个圆中,圆的周长与直径成正比例,圆的面积与半径成反比例。( )
19.天数一定,每天烧煤量和烧煤总量成反比例。( )
20.一条路,修了的米数和未修的米数成反比例。( )
21.某汽车行驶的路程一定,行驶的速度和所需要的时间成正比例。( )
22.电的单价一定,电费和用电量成反比例。( )
四、解方程
23.解比例。
15∶x=7∶28 ∶x=0.25∶8
= ∶=x∶
五、解答题
24.学校开展勤俭节约活动,同学们3天就节约零用钱450元。照这样计算,2021年7月份同学们能节约多少零用钱?(用比例解答)
25.一列磁悬浮列车匀速行驶时,行驶的路程与时间的关系如下。
时间/分 1 2 3 4 5 …
路程/千米 7 14 21 …
(1)完成上表。
(2)在下图中画出各点,并说一说各点连线的形状。
(3)从表中可得出,路程和时间成( )比例。
(4)当列车行驶2.5分时,路程是( )千米。
26.在一间布店的柜台上,有一张写着某种花布的米数和总价如下表。
数量(米) 1 2 3 4 5 6 ……
总价(元) 9.5 19 28.5 38 47.5 57
(1)表中有________和________两种量,他们是________的量。
(2)总价怎样随着数量的而变化而变化?
27.下图是甲、乙两人出行时路程与时间的关系图。
(1)甲每时行( )km,乙每时行( )km。
(2)甲行的路程与时间成比例吗?如果成比例,成什么比例?
(3)请你结合这幅图提出一个问题,并解答。
28.印刷厂准备把一批笔记本打包,运往商店。
包数/包 1 2 3 4 5 6 7 …
本数/本 40 80 120 …
(1)把上表填完整。
(2)先根据上表描点,再在下图顺次连接各点。
(3)笔记本的包数与本数成正比例吗?
(4)点(11,440)在这条直线上吗?这一点表示什么含义?
参考答案:
1.B
【详解】试题分析:A、要判断x与y是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;
B、根据比例的意义作答,即表示两个比相等的式子叫做比例;
C、根据比例的基本性质进行判断,即在比例中,两个外项的积等于两个内项的积.
解:A、因为=3y,
所以xy=(一定),
所以x与y成反比例;
B、24:36=;
0.6:=,
所以24:36与0.6:能组成比例;故题干错误;
C、因为在比例中,两个外项的积等于两个内项的积;
又因为互为倒数的两个数的乘积是1,
所以在比例里,若两个内项互为倒数,那么它的两个外项也互为倒数;
点评:此题主要考查了反比例、比例的意义及比例的基本性质.
2.B
【分析】根据反比例的意义,如果两种相关系的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例,以此判断。
【详解】①x+y=12,是和一定,所以x和y不成反比例;
②y=2x,则=2,是比值一定,所以x和y成正比例;
③=y,则xy=7,是积一定,所以x和y成反比例;
④25%∶y=x∶40中,根据比例的基本性质得:xy=25%×40,积一定,所以x和y成反比例。
表示x和y成反比例的式子有2个。
故答案为:B
【点睛】本题考查反比例的意义,灵活运用反比例意义解答问题。
3.A
【分析】根据正比例的意义:两种相关联的量中相对的两个数的比值一定,就是正比例关系,正比例的图形是一条经过原点的直线,购买鸡蛋的数量和总价成正比例关系,图像是经过原点的直线,据此解答。
【详解】A.,是经过原点的直线,是正比例图形;
B.,经过原点,但不是直线,不是正比例图形;
C.,经过原点,但不是直线,不是正比例图形。
故答案为:A
【点睛】根据正比例图形的特征进行解答。
4.B
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.平均速度×所需时间=从北京到广州的路程(乘积一定),所以从北京到广州,列车行驶的平均速度和所需时间成反比例关系;
B.人的体重和身高的乘积、比值均不一定,所以人的体重和身高不成比例;
C.圆锥的体积÷底面积=圆锥的高(一定),所以圆锥的高一定,它的体积和底面积成正比例关系。
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
5.C
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为行驶的速度×时间=路程(一定),所以行驶的速度和时间成反比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
6.B
【详解】试题分析:依据反比例的意义,即若两个量的乘积一定,则这两个量成反比例,从而可以作出正确选择.
解:选项A,不能判断a和c的积是否一定,所以a和c不成反比例;
选项B,ca=15(一定),则c和a成反比例;
选项C,不能判断a和c的积是否一定,所以a和c不成反比例;
点评:此题主要看c和a的积是否一定,若积一定,则成反比例,否则,不成反比例.
7.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.x+y=10,是和一定,不成比例;
B.x=y,即x:y=,是比值一定,则x和y成正比例;
C.y=(>0),即xy=6,是乘积一定,则x和y成反比例。
故选:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
8.总价,数量,正.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:=单价(一定),总价和数量成正比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
9.36,7,49,0..
【详解】试题分析:解答此题的关键是2.1:2.7,根据比的基本性质化成最简整数比是7:9,根据比与分数的关系,7:9=;根据比与除法的关系,7:9=7÷9,再根据商不变的性质,被除数、除数都乘4就是28÷36;根据比的基本性质,7:9的前、后项都乘7就是49:63;7÷9=0..由此进行转化并填空.
解:28÷36==2.1:2.7=49:63=0.
点评:此题考查除式、小数、分数、比之间的转化及循环小数的求法和写法.利用它们之间的关系和性质进行转化即可.
10. 正
【详解】略
11.√.
【详解】试题分析:分数形式的比例,分子、分母交叉相乘,积相等,改写成两数相乘的等式后,再根据正、反比例的意义,即可得答案.
解:=,
X×Y=5×9=45,
所以X和Y成反比例;
点评:此题主要考查正、反比例的意义及比例的基本性质.
12. 反 正
【详解】略
13.7:12,.
【详解】试题分析:根据甲数是乙数的57,可知甲乙两数的比是,5:7,可以把甲看作5,乙数看作7,再根据比的意义和分数除法的意义求解即可.
解:(1)由题意可知,甲乙两数的比是5:7,可以把甲看作5,乙数看作7,那么甲乙总数就是5+7=12,
则乙数与甲乙总数的比就是:7:12.
(2)甲乙两数的差是7﹣5=2,根据分数除法的意义可知,2÷5=.
点评:根据题意,知道甲乙两数的比是多少,可以把甲、乙看作一个具体的数,然后再根据比的意义和分数除法的意义就可以求出结果.
14. a b
【详解】略
15.╳
【分析】根据反比例的基本意义,成反比例的两个量乘积一定,据此判断即可。
【详解】单价=总价÷订阅的份数,比值一定,总价与订阅的份数成正比例而不是反比例。
故答案为:╳
【点睛】判断两个量成正比例还是反比例,根据比例的意义,首先找准不变量,再看两个变量是乘积一定还是比值一定,乘积一定的是反比例,比值一定的是正比例。
16.√
【详解】略
17.×
【分析】正反比例判断方法是:两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,它们的关系叫做正比例关系;如果两个量的积一定,它们的关系叫做反比例关系。
【详解】正方形面积=边长×边长;所以正方形面积÷边长=边长;因为正方形面积和边长都是变化的量,正方形面积与边长的比值不能确定,所以正方形面积与边长不成正比例关系。
故答案为:×
【点睛】根据正比例意义和辨别,以及正方形面积公式进行解答。
18.×
【分析】根据圆的周长公式C=πd可知:C÷d=π(一定),所以圆的周长与它的直径成正比例关系;
根据圆的面积公式S=πr2,S÷r2=π(一定),比值一定,所以圆的面积和半径的平方成正比例,而圆的面积与半径不成比例。
【详解】在同一个圆中,圆的周长与直径成正比例,圆的面积与半径不成比例。原题说法错误。
故答案为:×
【点睛】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
19.×
【详解】天数一定,每天烧煤量和烧煤总量成正比例。故原题干说法错误。
20.×
【分析】判断修了的米数和未修的米数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例。据此进行判断。
【详解】修了的米数+未修的米数=一条路的总米数(一定),是和一定,不是乘积一定,所以修了的米数和未修的米数不成反比例。
【点睛】此题属于辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断。
21.×
【分析】根据关系式路程=速度×时间判断即可。
【详解】路程=速度×时间,汽车行驶的路程一定,即速度与时间的乘积一定,所以行驶的速度和所需要的时间成反比例;原题说法错误。
故答案为:×
【点睛】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
22.×
【分析】两个相关联的量,若它们的比值一定,则它们成正比例关系;若它们的乘积一定,则它们成反比例关系;据此分析即可。
【详解】电费÷用电量=电的单价(一定),所以电的单价一定,电费和用电量成正比例。
故答案为:×
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
23.x=60;x=24;x=25;x=
【详解】略
24.4650元
【分析】根据题意可知,同学们每天节约的零用钱是一定的,7月份一共31天,列比例解答即可。
【详解】解:设7月份同学们能节约x元零用钱。
450∶3=x∶31
3x=13950
x=4650
答:2021年7月份同学们能节约4650元零用钱。
【点睛】此题考查了列比例解决实际问题,明确变化的两个量是比值一定还是乘积一定是解题关键。
25.(1)28;35
(2)各点在一条直线上
作图见详解
(3)正
(4)17.5
【分析】(1)通过读表可知:1分钟行驶了7千米;2分钟行驶了14千米,3分钟行驶了21千米,时间每增加1分钟路程就增加7千米,时间增加几倍路程就增加几倍。
(2)横轴表示时间,纵轴表示路程,根据统计表中的数据完成统计图。
(3)由图意可知,7∶1=7,14∶2=7,21∶3=7,28∶4=7……,速度是一定的,路程和时间的比值一定,路程÷时间=速度(一定),则路程与时间成正比例关系。
(4)根据:速度×时间=路程计算。
【详解】(1)21+7=28,28+7=35
时间/分 1 2 3 4 5 …
路程/千米 7 14 21 28 35 …
(2)如图:各点在一条直线上。
(3)从表中可得出,7∶1=7,14∶2=7,21∶3=7,28∶4=7……,路程÷时间=速度(一定),路程和时间成正比例。
(4)2.5×7=17.5(千米)
【点睛】此题属于辨识成正比例的量,就看这两个量对应的比值是否一定,以及正比例的图像。
26. 花布的米数 花布的总价 相关联 总价随着数量的增加而增加.
【详解】略
27.(1)12 24 (2)成比例,成正比例。
(3)甲、乙两人谁的速度更快? 乙的速度更快。(答案不唯一)
【解析】略
28.(1)见详解
(2)见详解
(3)成正比例
(4)在这条直线上;这一点表示11包有440本笔记本
【分析】(1)根据图中的信息可知,一包是40本,可以计算出表中的数据,再填表即可;
(2)根据画折线统计图的方法,找出各点的位置,再连线即可;
(3)判断两个相关的量成什么比例,就看这两个量对应的是比值一定,还是乘积一定,如果是比值一定,则成正比例;如果乘积一定,则成反比例,据此解答;
(4)根据横轴上代表的是包数,纵轴上代表的是本数,用本数除以包数,每一包的数一致,即在这条直线上,再根据统计图的信息解答即可。
【详解】(1)40×4=160(本)
40×5=200(本)
40×6=240(本)
40×7=280(本)
包数/包 1 2 3 4 5 6 7 …
本数/本 40 80 120 160 200 2400 280 …
(2)
(3)40÷1=40(本)
80÷2=40(本)
120÷3=40(本)
……
总本书÷书的包数=每包书中的本数(一定),书的包数与总本书×正比例。
(4)440÷11=40(本)
点(11,440)在这条直线上,这一点表示11包有440本笔记本。
【点睛】本题考查正比例意义和辨识,反比例意义和辨识;以及正比例的应用。
