2022--2023学年人教版八年级数学下册17.2 勾股定理的逆定理 同步训练(含答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学下册17.2 勾股定理的逆定理 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 17:02:29 | ||
图片预览

文档简介
17.2 勾股定理的逆定理
一、选择题
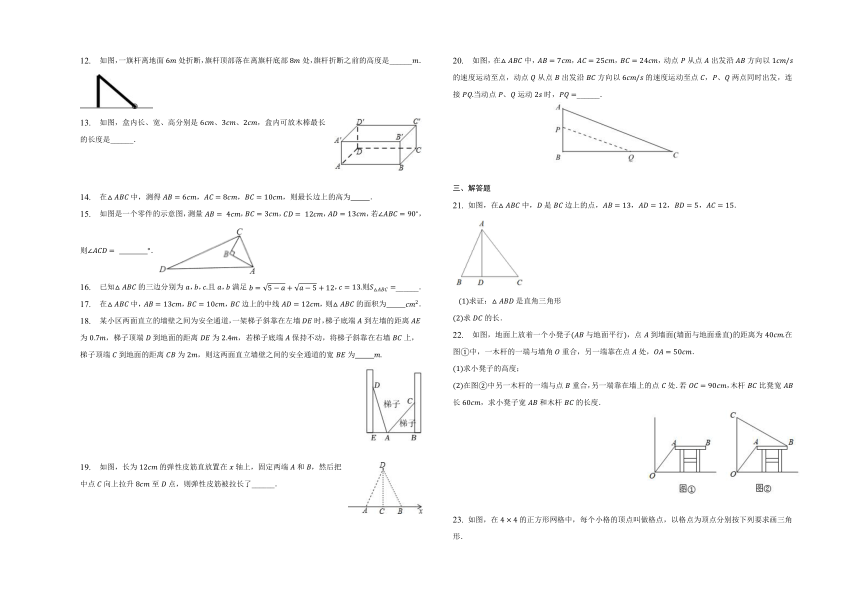
1. 在下列各数中,不是勾股数的是( )
A. ,, B. ,, C. ,, D.
2. 三角形的三边长为,,,且满足,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形
3. 在中,若,,的对边分别是,,,则下列条件中,不能判定是直角三角形的是 ( )
A. B.
C. ,, D.
4. 已知三角形三边长为,,,如果,则是( )
A. 以为斜边的直角三角形 B. 以为斜边的直角三角形
C. 以为斜边的直角三角形 D. 不是直角三角形
5. 九章算术中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈一丈尺,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部尺远,问折断处离地面的高度是多少?设折断处离地面的高度为尺,则可列方程为( )
A. B. C. D.
6. 如图所示,一文物被探明位于点地下处,由于点地面下有障碍物,考古人员不能垂直下挖,他们从距离点的处斜着挖掘,那么要找到文物至少要挖米.( )
A.
B.
C.
D.
7. 如图,一架米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端下滑米,则梯足将向外移( )
A. 米 B. 米 C. 米 D. 米
8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是,,,,,选取其中三块可重复选取按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A. ,,
B. ,,
C. ,,
D. ,,
9. 如图,将矩形沿折叠,使顶点恰好落在边的中点上.若,,则的长为( )
A. B. C. D.
10. 九章算术是古代东方数学代表作,书中记载:今有开门去阃读,门槛的意思一尺,不合二寸,问门广几何?题目大意是:如图、图为图的平面示意图,推开双门,双门间隙的距离为寸,点和点距离门槛都为尺尺寸,则的长是( )
A. 寸 B. 寸 C. 寸 D. 寸
二、填空题
11. 满足的三个正整数,称为勾股数.写出你比较熟悉的两组勾股数:______; ______.
12. 如图,一旗杆离地面处折断,旗杆顶部落在离旗杆底部处,旗杆折断之前的高度是______.
13. 如图,盒内长、宽、高分别是、、,盒内可放木棒最长的长度是______.
14. 在中,测得,,,则最长边上的高为 .
15. 如图是一个零件的示意图,测量,,,,若,则 .
16. 已知的三边分别为,,且,满足,则______.
17. 在中,,,边上的中线,则的面积为 .
18. 某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙时,梯子底端到左墙的距离为,梯子顶端到地面的距离为,若梯子底端保持不动,将梯子斜靠在右墙上,梯子顶端到地面的距离为,则这两面直立墙壁之间的安全通道的宽为
19. 如图,长为的弹性皮筋直放置在轴上,固定两端和,然后把中点向上拉升至点,则弹性皮筋被拉长了______.
20. 如图,在中,,,,动点从点出发沿方向以的速度运动至点,动点从点出发沿方向以的速度运动至点,、两点同时出发,连接当动点、运动时,______.
三、解答题
21. 如图,在中,是边上的点,,,,.
求证:是直角三角形
求的长.
22. 如图,地面上放着一个小凳子与地面平行,点到墙面墙面与地面垂直的距离为在图中,一木杆的一端与墙角重合,另一端靠在点处,.
求小凳子的高度;
在图中另一木杆的一端与点重合,另一端靠在墙上的点处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
23. 如图,在的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
在图中,画一个直角三角形,使它的三边长都是有理数;
在图中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;
在图中,画一个直角三角形,使它的三边长都是无理数.
24. 如图,一架长米的梯子,斜靠在竖直的墙上,这时梯子底端离墙米.
此时梯子顶端离地面多少米?
若梯子顶端下滑米,那么梯子底端将向左滑动多少米?
25. 已知:在中,、、所对的边分别记作、、如图,分别以的三条边为边长向外作正方形,其正方形的面积由小到大分别记作、、,则有;
如图,分别以的三条边为直径向外作半圆,其半圆的面积由小到大分别记作、、,请问与有怎样的数量关系,并证明你的结论;
分别以直角三角形的三条边为直径作半圆,如图所示,其面积由小到大分别记作、、,根据中的探索,直接回答与有怎样的数量关系;
若中,,,求出图中阴影部分的面积.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ;
11、,,; ,, ; 12、 ; 13、 ; 14、 ; 15、 ; 16、 ; 17、 ; 18、 ; 19、 ; 20、
21、证明:,,,
,
是直角三角形,即;
解:,
是直角三角形,
在中,.
22、解:过作垂直于墙面,垂足,
根据题意可得,,
在中,,
即凳子的高度为.
延长交墙面于点,可得,
设,则,,,
在中,,即,
解得,则.
23、解:如图中,即为所求.
如图中,即为所求.
即为所求.
24、解:米,米,
中,,
梯子顶端距离地面的高度米.
答:此时梯子顶端离地面米;
梯子顶端下滑了米,
即梯子顶端距离地面的高度米,
中,,
米,
米,即下端滑行了米.
答:梯子底端将向左滑动了米.
25、解:,
根据勾股定理可知:;
;
.
一、选择题
1. 在下列各数中,不是勾股数的是( )
A. ,, B. ,, C. ,, D.
2. 三角形的三边长为,,,且满足,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形
3. 在中,若,,的对边分别是,,,则下列条件中,不能判定是直角三角形的是 ( )
A. B.
C. ,, D.
4. 已知三角形三边长为,,,如果,则是( )
A. 以为斜边的直角三角形 B. 以为斜边的直角三角形
C. 以为斜边的直角三角形 D. 不是直角三角形
5. 九章算术中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈一丈尺,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部尺远,问折断处离地面的高度是多少?设折断处离地面的高度为尺,则可列方程为( )
A. B. C. D.
6. 如图所示,一文物被探明位于点地下处,由于点地面下有障碍物,考古人员不能垂直下挖,他们从距离点的处斜着挖掘,那么要找到文物至少要挖米.( )
A.
B.
C.
D.
7. 如图,一架米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端下滑米,则梯足将向外移( )
A. 米 B. 米 C. 米 D. 米
8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是,,,,,选取其中三块可重复选取按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A. ,,
B. ,,
C. ,,
D. ,,
9. 如图,将矩形沿折叠,使顶点恰好落在边的中点上.若,,则的长为( )
A. B. C. D.
10. 九章算术是古代东方数学代表作,书中记载:今有开门去阃读,门槛的意思一尺,不合二寸,问门广几何?题目大意是:如图、图为图的平面示意图,推开双门,双门间隙的距离为寸,点和点距离门槛都为尺尺寸,则的长是( )
A. 寸 B. 寸 C. 寸 D. 寸
二、填空题
11. 满足的三个正整数,称为勾股数.写出你比较熟悉的两组勾股数:______; ______.
12. 如图,一旗杆离地面处折断,旗杆顶部落在离旗杆底部处,旗杆折断之前的高度是______.
13. 如图,盒内长、宽、高分别是、、,盒内可放木棒最长的长度是______.
14. 在中,测得,,,则最长边上的高为 .
15. 如图是一个零件的示意图,测量,,,,若,则 .
16. 已知的三边分别为,,且,满足,则______.
17. 在中,,,边上的中线,则的面积为 .
18. 某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙时,梯子底端到左墙的距离为,梯子顶端到地面的距离为,若梯子底端保持不动,将梯子斜靠在右墙上,梯子顶端到地面的距离为,则这两面直立墙壁之间的安全通道的宽为
19. 如图,长为的弹性皮筋直放置在轴上,固定两端和,然后把中点向上拉升至点,则弹性皮筋被拉长了______.
20. 如图,在中,,,,动点从点出发沿方向以的速度运动至点,动点从点出发沿方向以的速度运动至点,、两点同时出发,连接当动点、运动时,______.
三、解答题
21. 如图,在中,是边上的点,,,,.
求证:是直角三角形
求的长.
22. 如图,地面上放着一个小凳子与地面平行,点到墙面墙面与地面垂直的距离为在图中,一木杆的一端与墙角重合,另一端靠在点处,.
求小凳子的高度;
在图中另一木杆的一端与点重合,另一端靠在墙上的点处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
23. 如图,在的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
在图中,画一个直角三角形,使它的三边长都是有理数;
在图中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;
在图中,画一个直角三角形,使它的三边长都是无理数.
24. 如图,一架长米的梯子,斜靠在竖直的墙上,这时梯子底端离墙米.
此时梯子顶端离地面多少米?
若梯子顶端下滑米,那么梯子底端将向左滑动多少米?
25. 已知:在中,、、所对的边分别记作、、如图,分别以的三条边为边长向外作正方形,其正方形的面积由小到大分别记作、、,则有;
如图,分别以的三条边为直径向外作半圆,其半圆的面积由小到大分别记作、、,请问与有怎样的数量关系,并证明你的结论;
分别以直角三角形的三条边为直径作半圆,如图所示,其面积由小到大分别记作、、,根据中的探索,直接回答与有怎样的数量关系;
若中,,,求出图中阴影部分的面积.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ;
11、,,; ,, ; 12、 ; 13、 ; 14、 ; 15、 ; 16、 ; 17、 ; 18、 ; 19、 ; 20、
21、证明:,,,
,
是直角三角形,即;
解:,
是直角三角形,
在中,.
22、解:过作垂直于墙面,垂足,
根据题意可得,,
在中,,
即凳子的高度为.
延长交墙面于点,可得,
设,则,,,
在中,,即,
解得,则.
23、解:如图中,即为所求.
如图中,即为所求.
即为所求.
24、解:米,米,
中,,
梯子顶端距离地面的高度米.
答:此时梯子顶端离地面米;
梯子顶端下滑了米,
即梯子顶端距离地面的高度米,
中,,
米,
米,即下端滑行了米.
答:梯子底端将向左滑动了米.
25、解:,
根据勾股定理可知:;
;
.
