第十六章二次根式单元检测(含答案) 2022-2023学年 人教版八年级数学下册
文档属性
| 名称 | 第十六章二次根式单元检测(含答案) 2022-2023学年 人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 17:49:06 | ||
图片预览



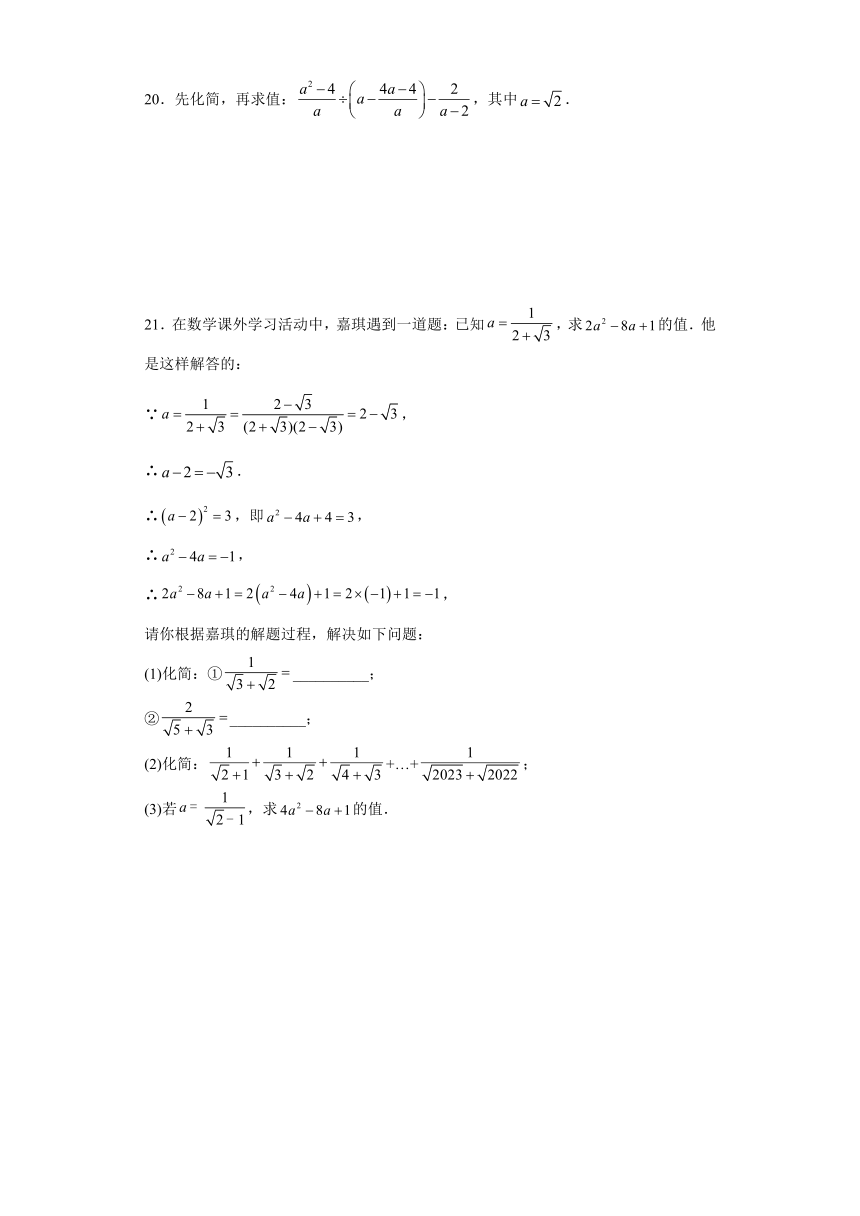
文档简介
二次根式单元检测
一、单选题
1.下面式子是二次根式的是( )
A. B. C. D.a
2.若是整数,则正整数n的最小值是( )
A.2 B.3 C.4 D.6
3.若,化简的结果是( )
A. B. C. D.
4.计算的结果为( )
A. B. C. D.
5.下列二次根式中,最简二次根式是( )
A. B. C. D.
6.下列各式计算正确的是( )
A. B.
C. D.
7.下列二次根式不能与合并的是( )
A. B. C. D.
8.下列计算,正确的是( )
A. B.
C. D.
9.已知,,,那么,,的大小关系是( )
A. B. C. D.
10.如图,矩形内有两个相邻的白色正方形,其面积分别为2和18,则图中阴影部分的面积为( )
A. B. C.4 D.6
二、填空题
11.若式子在实数范围内有意义,则的取值范围是__________.
12.代数式的最小值为__________.
13.①比较大小:________(填“”、“”、“”),
②化简________.
14.若最简二次根式与最简二次根式相等,则___________.
15.已知,,则代数式的值等于__________.
16.请阅读材料,并解决实际问题:海伦(约公元50年),古希腊几何学家,利用三角形的三边求面积:有一个三角形的三条边长分别为a,b,c,记p=,那么这个三角形的面积S=.这个公式称海伦公式.秦九韶(约1202﹣1261),我国南宋时期的数学家,曾提出利用三角形的三边求面积的秦九韶公式S=.通过公式变形,可以发现它们实质是同一公式,所以海伦公式也称海伦﹣秦九韶公式.
问题:在△ABC中,AC=5,AB=6,BC=7,用海伦﹣秦九韶公式求△ABC的面积为 _____.
三、解答题
17.计算
(1)
(2)
(3)
(4)
18.表示实数a,b的点在数轴上的位置如图所示,化简代数式的值.
19.已知二次根式.
(1)求使得该二次根式有意义的的取值范围;
(2)已知是最简二次根式,且与可以合并.
①求的值;
②求与的乘积.
20.先化简,再求值:,其中.
21.在数学课外学习活动中,嘉琪遇到一道题:已知,求的值.他是这样解答的:
∵,
∴.
∴,即,
∴,
∴,
请你根据嘉琪的解题过程,解决如下问题:
(1)化简:①__________;
②__________;
(2)化简:+…+;
(3)若,求的值.
22.高空抛物严重威胁着人们的“头顶安全”,即便是常见小物件,一旦高空落下,也威力惊人,而且用时很短,常常避让不及.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式(不考虑风速的影响,).
(1)求从40m高空抛物到落地的时间.(结果保留根号)
(2)已知高空抛物动能(单位:J)物体质量(单位:kg)高度(单位:m),某质量为0.2kg的玩具在高空被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗?请说明理由.(注:伤害无防护人体只需要65J的动能)
23.先观察等式,再解答问题:
①;
②;
③.
(1)请你根据以上三个等式提供的信息,猜想的结果,并验证;
(2)请你按照以上各等式反映的规律,试写出用含的式子表示的等式(为正整数).
答案
1.A
2.B
3.D
4.B
5.A
6.B
7.D
8.C
9.A
10.C
11.
12.2
13.
14.
15.
16.
17.(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
18.由图可知:,
原式
.
19.(1)解:二次根式有意义,
,
解得;
(2)解:①,
与能合并,并且是最简二次根式,
,
解得;
②由①可得.
20.解:原式
把代入得
.
21.(1)解:①;
②,
故答案为:,;
(2)解:
;
(3)解:∵,
∴,
∴,即,
∴.
22.(1)解:当时,;
(2)这个玩具产生的动能会伤害到楼下的行人,理由如下:
当时,,
解得,
∴高空抛物动能,
∴这个玩具产生的动能会伤害到楼下的行人.
23.(1)解:的结果为;
验证:.
(2).
一、单选题
1.下面式子是二次根式的是( )
A. B. C. D.a
2.若是整数,则正整数n的最小值是( )
A.2 B.3 C.4 D.6
3.若,化简的结果是( )
A. B. C. D.
4.计算的结果为( )
A. B. C. D.
5.下列二次根式中,最简二次根式是( )
A. B. C. D.
6.下列各式计算正确的是( )
A. B.
C. D.
7.下列二次根式不能与合并的是( )
A. B. C. D.
8.下列计算,正确的是( )
A. B.
C. D.
9.已知,,,那么,,的大小关系是( )
A. B. C. D.
10.如图,矩形内有两个相邻的白色正方形,其面积分别为2和18,则图中阴影部分的面积为( )
A. B. C.4 D.6
二、填空题
11.若式子在实数范围内有意义,则的取值范围是__________.
12.代数式的最小值为__________.
13.①比较大小:________(填“”、“”、“”),
②化简________.
14.若最简二次根式与最简二次根式相等,则___________.
15.已知,,则代数式的值等于__________.
16.请阅读材料,并解决实际问题:海伦(约公元50年),古希腊几何学家,利用三角形的三边求面积:有一个三角形的三条边长分别为a,b,c,记p=,那么这个三角形的面积S=.这个公式称海伦公式.秦九韶(约1202﹣1261),我国南宋时期的数学家,曾提出利用三角形的三边求面积的秦九韶公式S=.通过公式变形,可以发现它们实质是同一公式,所以海伦公式也称海伦﹣秦九韶公式.
问题:在△ABC中,AC=5,AB=6,BC=7,用海伦﹣秦九韶公式求△ABC的面积为 _____.
三、解答题
17.计算
(1)
(2)
(3)
(4)
18.表示实数a,b的点在数轴上的位置如图所示,化简代数式的值.
19.已知二次根式.
(1)求使得该二次根式有意义的的取值范围;
(2)已知是最简二次根式,且与可以合并.
①求的值;
②求与的乘积.
20.先化简,再求值:,其中.
21.在数学课外学习活动中,嘉琪遇到一道题:已知,求的值.他是这样解答的:
∵,
∴.
∴,即,
∴,
∴,
请你根据嘉琪的解题过程,解决如下问题:
(1)化简:①__________;
②__________;
(2)化简:+…+;
(3)若,求的值.
22.高空抛物严重威胁着人们的“头顶安全”,即便是常见小物件,一旦高空落下,也威力惊人,而且用时很短,常常避让不及.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式(不考虑风速的影响,).
(1)求从40m高空抛物到落地的时间.(结果保留根号)
(2)已知高空抛物动能(单位:J)物体质量(单位:kg)高度(单位:m),某质量为0.2kg的玩具在高空被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗?请说明理由.(注:伤害无防护人体只需要65J的动能)
23.先观察等式,再解答问题:
①;
②;
③.
(1)请你根据以上三个等式提供的信息,猜想的结果,并验证;
(2)请你按照以上各等式反映的规律,试写出用含的式子表示的等式(为正整数).
答案
1.A
2.B
3.D
4.B
5.A
6.B
7.D
8.C
9.A
10.C
11.
12.2
13.
14.
15.
16.
17.(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
18.由图可知:,
原式
.
19.(1)解:二次根式有意义,
,
解得;
(2)解:①,
与能合并,并且是最简二次根式,
,
解得;
②由①可得.
20.解:原式
把代入得
.
21.(1)解:①;
②,
故答案为:,;
(2)解:
;
(3)解:∵,
∴,
∴,即,
∴.
22.(1)解:当时,;
(2)这个玩具产生的动能会伤害到楼下的行人,理由如下:
当时,,
解得,
∴高空抛物动能,
∴这个玩具产生的动能会伤害到楼下的行人.
23.(1)解:的结果为;
验证:.
(2).
