第一章 回顾与思考 导学案(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
回顾与思考
【学习目标】
1.认识常见几何体的基本特性,能对这些几何体进行正确的识别和简单的分类;
2.经历展开与折叠、切截以及从不同方向看等数学活动,积累数学活动经验;
3.通过丰富的实例,进一步认识点、线、面,了解有关点、线及某些平面图形的一些简单性质;
4.初步体会从不同方向观察同一物体时可能看到不同的图形,能识别简单物体的三种视力(主视图、俯视图和左视图),会画立方体(正方体)及其简单组合体的三种视图.
【课前梳理】
1.几何体的分类方法有:_________________________________________________.
2.六棱柱有___________个顶点,________条棱_________个面.
3.图形是由点、线、面构成的.点动________,线动________,面动________.
4.展开与折叠
(1)正方体的展开图由六个___组成,棱柱的展开图由_ _个底面和_ _个长方形组成;
(2)圆锥的展开图由一个______和一个______组成;
(3)圆柱的展开图是两个______和一个______组成.
5.截一个几何体
(1)用一个平面去截几何体,截出的面叫做_______________,同一个几何体不同的截法会有不同的___________;一般地,截面与几何体的几个面相交,就得到_____条交线,截面就是_________边形.
(2)用一个平面去截一个正方体或长方体,截面有 、 、 、 等.
(3)用一个平面去截一个圆柱所得到的截面有 、 、 、 还有一种像拱形的门得形状.
(4)用一个平面截圆锥,可以得到 、 、 及类似拱形形状.
6.几种几何体的从三个方向看到的图形:
(1)正方体的从三个方向看到的图形都是__________(2)球体的从三个方向看到的图形都是________.
(3)圆柱体:从正在面看到的图形、从左面看到的图形都是同样大小的__________,从上面看到的图形是__________.
(4)圆锥体:从正在面看到的图形、从左面看到的图形都是同样大小的__________,从上面看到的图形是__________.
【课堂练习】
典型例题1:如图是某个几何体的展开图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.三棱柱
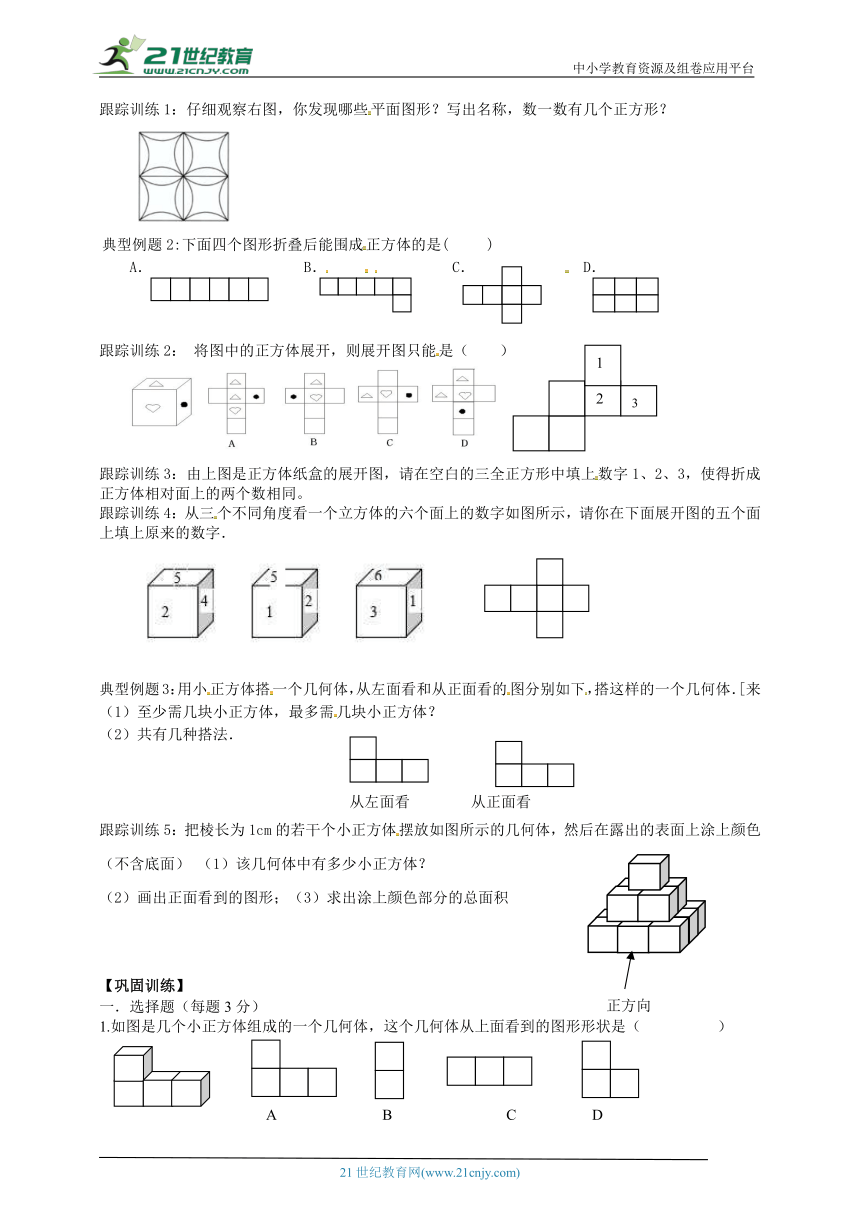
跟踪训练1:仔细观察右图,你发现哪些平面图形?写出名称,数一数有几个正方形?
典型例题2:下面四个图形折叠后能围成正方体的是( )
A. B. C. D.
跟踪训练2: 将图中的正方体展开,则展开图只能是( )
跟踪训练3:由上图是正方体纸盒的展开图,请在空白的三全正方形中填上数字1、2、3,使得折成正方体相对面上的两个数相同。
跟踪训练4:从三个不同角度看一个立方体的六个面上的数字如图所示,请你在下面展开图的五个面上填上原来的数字.
典型例题3:用小正方体搭一个几何体,从左面看和从正面看的图分别如下,搭这样的一个几何体.[来
至少需几块小正方体,最多需几块小正方体?
(2)共有几种搭法.
从左面看 从正面看
跟踪训练5:把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色(不含底面) (1)该几何体中有多少小正方体?
(2)画出正面看到的图形;(3)求出涂上颜色部分的总面积
【巩固训练】
一.选择题(每题3分)
1.如图是几个小正方体组成的一个几何体,这个几何体从上面看到的图形形状是( )
A B C D
2.如图是教师每天在黑板上书写用的粉笔,从正面看到的形状是( )
A B C D
3.如图是由几个相同小立方体搭成的几何体从三个方向看到的形状,则这个几何体的小立方体的个数是( )
从正面看 从左面看 从上面看
A. 4 B. 5 C. 6 D. 7
4.下面几何体的截面图不可能是圆的是( )
A. 圆柱 B. 圆锥 C. 球 D. 棱柱
5.正方体的截面不可能是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
6.用一个平面去截一个几何体,截面都是圆,那么这个几何体是( )
A. 圆柱 B. 圆锥 C. 三棱柱 D. 球
二、填空题(每空3分)
7.水平放置的正方体的6个面,分别用“前面、后面、上面、下面、左面、右面”表示。如图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示 面。
8.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是_______。
9.一个几何体的顶点数是8,棱数是12,面数应是________________.
10.将下列几何体分类,柱体有_________________,椎体有________________.
11.如图分别是几个相同小立方体搭成的几何体,分别是从正面和从左面看到的形状图,则这个几何体的小立方体的个数最多是____________,最少是____________.
从正面看
从左面看
回顾与思考
【课堂练习】
典型例题1:( B )跟踪训练1:扇形、弧形、正方形,5个
典型例题2: ( C ) 跟踪训练2:(A) 跟踪训练3:略 跟踪训练4:略.
典型例题3:略
跟踪训练5: (1)该几何体中正方体的个数为9+4+1=14个;
(2) ( https: / / gss0. / 7Po3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / b21bb051f81986182118283549ed2e738bd4e620.jpg" \o "\"点击查看大图\" \t "_blank );
(3)先算侧面--底层12个小面 中层8个 上层4个
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个总共33个小面.
【巩固训练】
一.选择题(每题3分)
1.( C )2.( C )3.( B )4.( D )5.( D )6.( D )
二、填空题(每空3分)
7. 上 .m] 8. __6__. 9. ____四棱柱___.
10. __(1)(2)(6)(7)____, ___(5)(8)(9)__.
11. ___13___, ___9__.
2
3
1
正方向
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
回顾与思考
【学习目标】
1.认识常见几何体的基本特性,能对这些几何体进行正确的识别和简单的分类;
2.经历展开与折叠、切截以及从不同方向看等数学活动,积累数学活动经验;
3.通过丰富的实例,进一步认识点、线、面,了解有关点、线及某些平面图形的一些简单性质;
4.初步体会从不同方向观察同一物体时可能看到不同的图形,能识别简单物体的三种视力(主视图、俯视图和左视图),会画立方体(正方体)及其简单组合体的三种视图.
【课前梳理】
1.几何体的分类方法有:_________________________________________________.
2.六棱柱有___________个顶点,________条棱_________个面.
3.图形是由点、线、面构成的.点动________,线动________,面动________.
4.展开与折叠
(1)正方体的展开图由六个___组成,棱柱的展开图由_ _个底面和_ _个长方形组成;
(2)圆锥的展开图由一个______和一个______组成;
(3)圆柱的展开图是两个______和一个______组成.
5.截一个几何体
(1)用一个平面去截几何体,截出的面叫做_______________,同一个几何体不同的截法会有不同的___________;一般地,截面与几何体的几个面相交,就得到_____条交线,截面就是_________边形.
(2)用一个平面去截一个正方体或长方体,截面有 、 、 、 等.
(3)用一个平面去截一个圆柱所得到的截面有 、 、 、 还有一种像拱形的门得形状.
(4)用一个平面截圆锥,可以得到 、 、 及类似拱形形状.
6.几种几何体的从三个方向看到的图形:
(1)正方体的从三个方向看到的图形都是__________(2)球体的从三个方向看到的图形都是________.
(3)圆柱体:从正在面看到的图形、从左面看到的图形都是同样大小的__________,从上面看到的图形是__________.
(4)圆锥体:从正在面看到的图形、从左面看到的图形都是同样大小的__________,从上面看到的图形是__________.
【课堂练习】
典型例题1:如图是某个几何体的展开图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.三棱柱
跟踪训练1:仔细观察右图,你发现哪些平面图形?写出名称,数一数有几个正方形?
典型例题2:下面四个图形折叠后能围成正方体的是( )
A. B. C. D.
跟踪训练2: 将图中的正方体展开,则展开图只能是( )
跟踪训练3:由上图是正方体纸盒的展开图,请在空白的三全正方形中填上数字1、2、3,使得折成正方体相对面上的两个数相同。
跟踪训练4:从三个不同角度看一个立方体的六个面上的数字如图所示,请你在下面展开图的五个面上填上原来的数字.
典型例题3:用小正方体搭一个几何体,从左面看和从正面看的图分别如下,搭这样的一个几何体.[来
至少需几块小正方体,最多需几块小正方体?
(2)共有几种搭法.
从左面看 从正面看
跟踪训练5:把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色(不含底面) (1)该几何体中有多少小正方体?
(2)画出正面看到的图形;(3)求出涂上颜色部分的总面积
【巩固训练】
一.选择题(每题3分)
1.如图是几个小正方体组成的一个几何体,这个几何体从上面看到的图形形状是( )
A B C D
2.如图是教师每天在黑板上书写用的粉笔,从正面看到的形状是( )
A B C D
3.如图是由几个相同小立方体搭成的几何体从三个方向看到的形状,则这个几何体的小立方体的个数是( )
从正面看 从左面看 从上面看
A. 4 B. 5 C. 6 D. 7
4.下面几何体的截面图不可能是圆的是( )
A. 圆柱 B. 圆锥 C. 球 D. 棱柱
5.正方体的截面不可能是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
6.用一个平面去截一个几何体,截面都是圆,那么这个几何体是( )
A. 圆柱 B. 圆锥 C. 三棱柱 D. 球
二、填空题(每空3分)
7.水平放置的正方体的6个面,分别用“前面、后面、上面、下面、左面、右面”表示。如图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示 面。
8.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是_______。
9.一个几何体的顶点数是8,棱数是12,面数应是________________.
10.将下列几何体分类,柱体有_________________,椎体有________________.
11.如图分别是几个相同小立方体搭成的几何体,分别是从正面和从左面看到的形状图,则这个几何体的小立方体的个数最多是____________,最少是____________.
从正面看
从左面看
回顾与思考
【课堂练习】
典型例题1:( B )跟踪训练1:扇形、弧形、正方形,5个
典型例题2: ( C ) 跟踪训练2:(A) 跟踪训练3:略 跟踪训练4:略.
典型例题3:略
跟踪训练5: (1)该几何体中正方体的个数为9+4+1=14个;
(2) ( https: / / gss0. / 7Po3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / b21bb051f81986182118283549ed2e738bd4e620.jpg" \o "\"点击查看大图\" \t "_blank );
(3)先算侧面--底层12个小面 中层8个 上层4个
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个总共33个小面.
【巩固训练】
一.选择题(每题3分)
1.( C )2.( C )3.( B )4.( D )5.( D )6.( D )
二、填空题(每空3分)
7. 上 .m] 8. __6__. 9. ____四棱柱___.
10. __(1)(2)(6)(7)____, ___(5)(8)(9)__.
11. ___13___, ___9__.
2
3
1
正方向
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
