7.1.1条件概率公式 课件(共23张PPT)
文档属性
| 名称 | 7.1.1条件概率公式 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 18:49:17 | ||
图片预览







文档简介
(共23张PPT)
7.1.1条件概率
01
02
03
04
事件A与B至少有一个发生的事件叫做事件A与B的和事件,记为AUB(或A+B);
若事件A与事件B互斥,则 P(AUB)=P(A)+P(B);
事件A与B同时发生的事件叫做事件A与B的积事件,记为A∩B(或AB).
若AB为不可能事件,则说事件A与事件B互斥;
复习回顾
PART TWO
第一部分
导
基本要求:
1.阅读课本 通过具体实例的研究,能说出条件概率和简单随机事件概率的区别。
2.阅读课本,能说出条件概率和事件独立性的关系以及概率的乘法公式。
3.阅读课本中间部分,能说出条件概率的性质
4.阅读课本-例题,能应用条件概率的公式和乘法公式计算简单的条件概率和积事件的概率,类比例题完成课本48页2,3
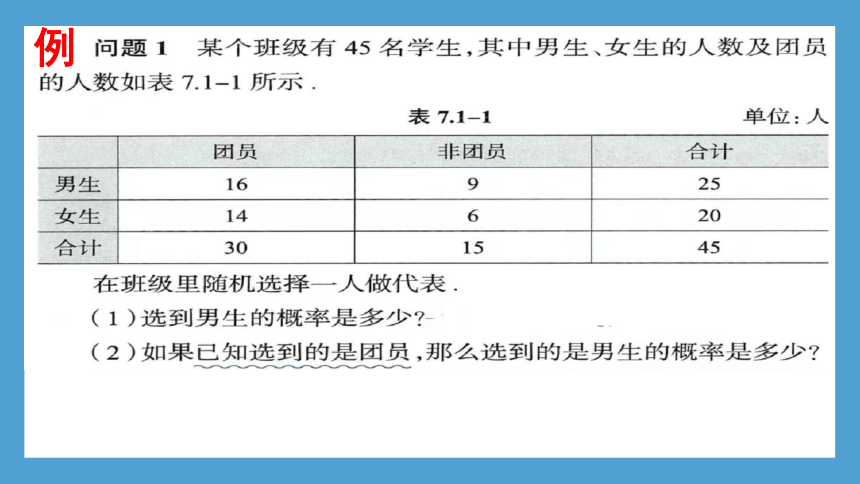
例
1. 条件概率
(1)定义:一般地,设A,B为两个随机事件,且P(A)>0,我们称 为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
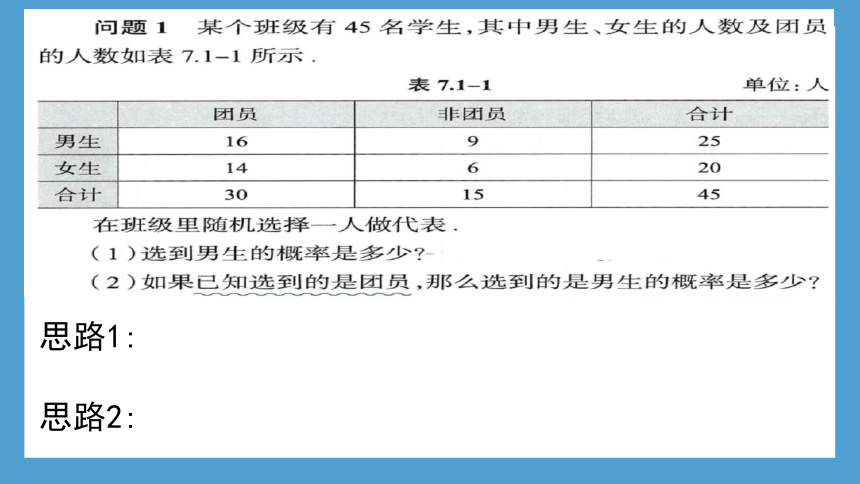
思路1:
思路2:
1. 条件概率
(2)特例:当P(A)>0时,当且仅当事件A与B相互独立时,有P(B|A)=P(B).
2. 概率的乘法公式
对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)·P(B|A).
例
PART TWO
第三部分
议
大胆展示你的疑惑!
有惑才有得!
我提问、我展示、
我质疑、我补充。
PART TWO
第四部分
结
本节课需要掌握的内容:
1.条件概率公式。
2.概率的乘法公式。
3.条件概率的性质。
PART TWO
第五部分
练
1.甲、乙两市都位于长江下游,根据一百多年来的气象记录,知道一年中下雨天的比例甲市占20%,乙市占18%,两地同时下雨占12%,记P(A)=0.2,P(B)=0.18,P(AB)=0.12,则P(A|B)和P(B|A)分别等于( )
2.盒中装有5个产品,其中3个一等品,2个二等品,不放回地从中取产品,每次取1个,取两次.求:
(1)两次都取得一等品的概率;
(2)第二次取得一等品的概率;
(3)已知在第二次取得一等品的条件下,第一次取得的是二等品的概率.
3.袋中装有大小相同的6个黄色的乒乓球,4个白色的乒乓球,每次抽取一球,取后不放回,连取两次,求在第一次取到白球的条件下第二次取到黄球的概率.
THANK
YOU
7.1.1条件概率
01
02
03
04
事件A与B至少有一个发生的事件叫做事件A与B的和事件,记为AUB(或A+B);
若事件A与事件B互斥,则 P(AUB)=P(A)+P(B);
事件A与B同时发生的事件叫做事件A与B的积事件,记为A∩B(或AB).
若AB为不可能事件,则说事件A与事件B互斥;
复习回顾
PART TWO
第一部分
导
基本要求:
1.阅读课本 通过具体实例的研究,能说出条件概率和简单随机事件概率的区别。
2.阅读课本,能说出条件概率和事件独立性的关系以及概率的乘法公式。
3.阅读课本中间部分,能说出条件概率的性质
4.阅读课本-例题,能应用条件概率的公式和乘法公式计算简单的条件概率和积事件的概率,类比例题完成课本48页2,3
例
1. 条件概率
(1)定义:一般地,设A,B为两个随机事件,且P(A)>0,我们称 为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
思路1:
思路2:
1. 条件概率
(2)特例:当P(A)>0时,当且仅当事件A与B相互独立时,有P(B|A)=P(B).
2. 概率的乘法公式
对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)·P(B|A).
例
PART TWO
第三部分
议
大胆展示你的疑惑!
有惑才有得!
我提问、我展示、
我质疑、我补充。
PART TWO
第四部分
结
本节课需要掌握的内容:
1.条件概率公式。
2.概率的乘法公式。
3.条件概率的性质。
PART TWO
第五部分
练
1.甲、乙两市都位于长江下游,根据一百多年来的气象记录,知道一年中下雨天的比例甲市占20%,乙市占18%,两地同时下雨占12%,记P(A)=0.2,P(B)=0.18,P(AB)=0.12,则P(A|B)和P(B|A)分别等于( )
2.盒中装有5个产品,其中3个一等品,2个二等品,不放回地从中取产品,每次取1个,取两次.求:
(1)两次都取得一等品的概率;
(2)第二次取得一等品的概率;
(3)已知在第二次取得一等品的条件下,第一次取得的是二等品的概率.
3.袋中装有大小相同的6个黄色的乒乓球,4个白色的乒乓球,每次抽取一球,取后不放回,连取两次,求在第一次取到白球的条件下第二次取到黄球的概率.
THANK
YOU
