2022—2023学年北师大版数学九年级下册第三章圆 复习练习(含解析)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级下册第三章圆 复习练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 561.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 07:50:00 | ||
图片预览



文档简介
初中数学试卷 第三章圆
一、单选题
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π
2.如图,已知点 、 、 都在 上, ,则 的度数是( )
A. B. C. D.
3.已知,如图,点 C、D 在⊙O 上,直径 AB=6 cm,弦 AC,BD 相交于点 E.若 CE=BC, 则阴影部分面积为( )
A.p - B. p -
C. p - D. p -
4.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
5.如图, 为 的外接圆,已知 为130°,则 的度数为( )
A.50° B.80° C.100° D.115°
6.如图,⊙O的半径为3, 是⊙O的内接三角形,过点A作AD垂直BC于点D.若 , ,则 长是( )
A. B.4 C. D.
7.下列说法正确的是( )
A.圆的任意一条直径都是它的对称轴
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆中最长的弦是直径
8.如图,AB是⊙O的直径,点C、D在圆O上,且OC DB,连接AD、CD,若∠C=28°,则∠A的大小为( )
A.30° B.28° C.24° D.34°
9.如图,⊙O是△ABC的外接圆,直径BD长为4,sin∠BAC=,则BC的长为( )
A. B.3 C. D.
10.如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米.
A. B. C. D.
二、填空题
11.已知圆的半径为2,则60°圆心角所对的弧长为 .
12. 150°的圆心角所对的弧长是5πcm,则此弧所在圆的半径是 cm.
13.如图,在 中, , , ,以 为圆心, 为半径画弧交 的延长线与点 ,则弧 的长为 .
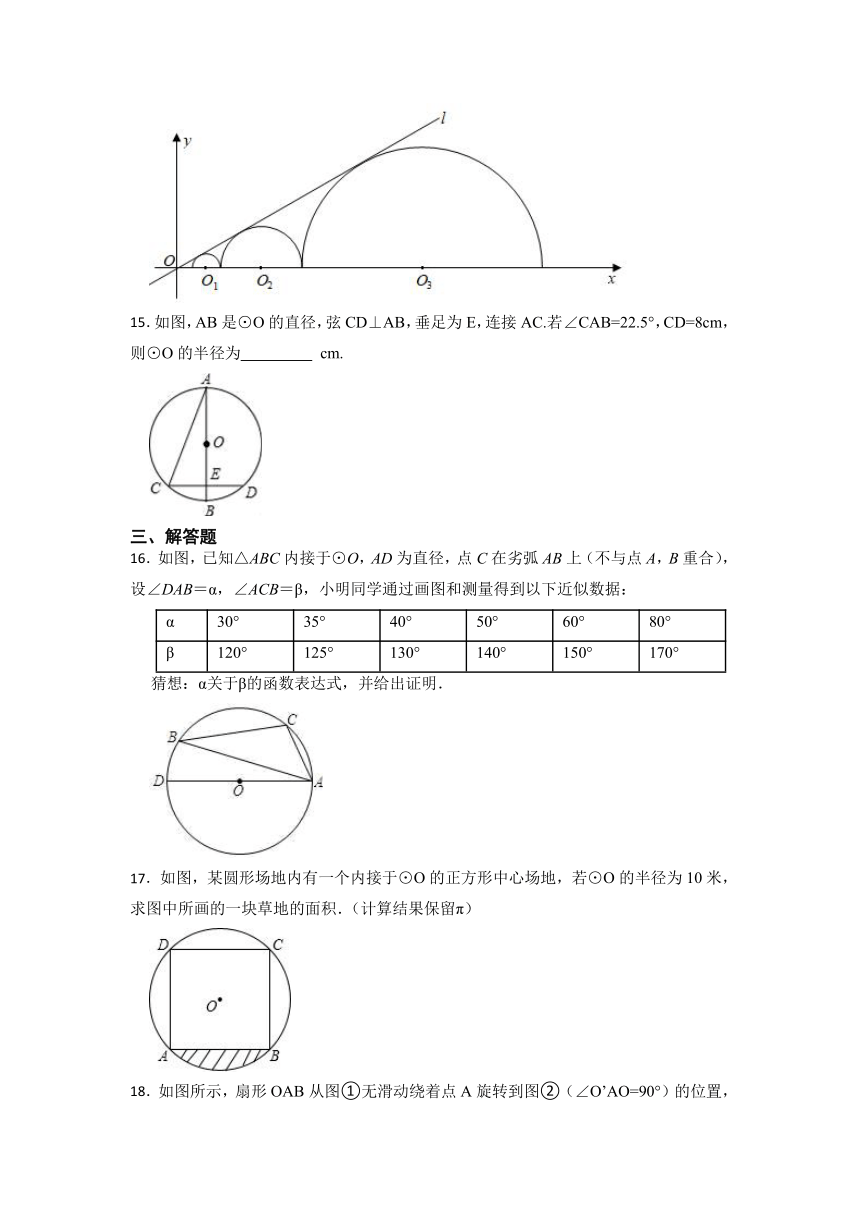
14.如图,圆心都在 轴正半轴上的半圆 ,半圆 ,……半圆 与直线l相切.设半圆 ,半圆 ,……,半圆 的半径分别是 , ,……, ,则当直线l与x轴所成锐角为 ,且 时, .
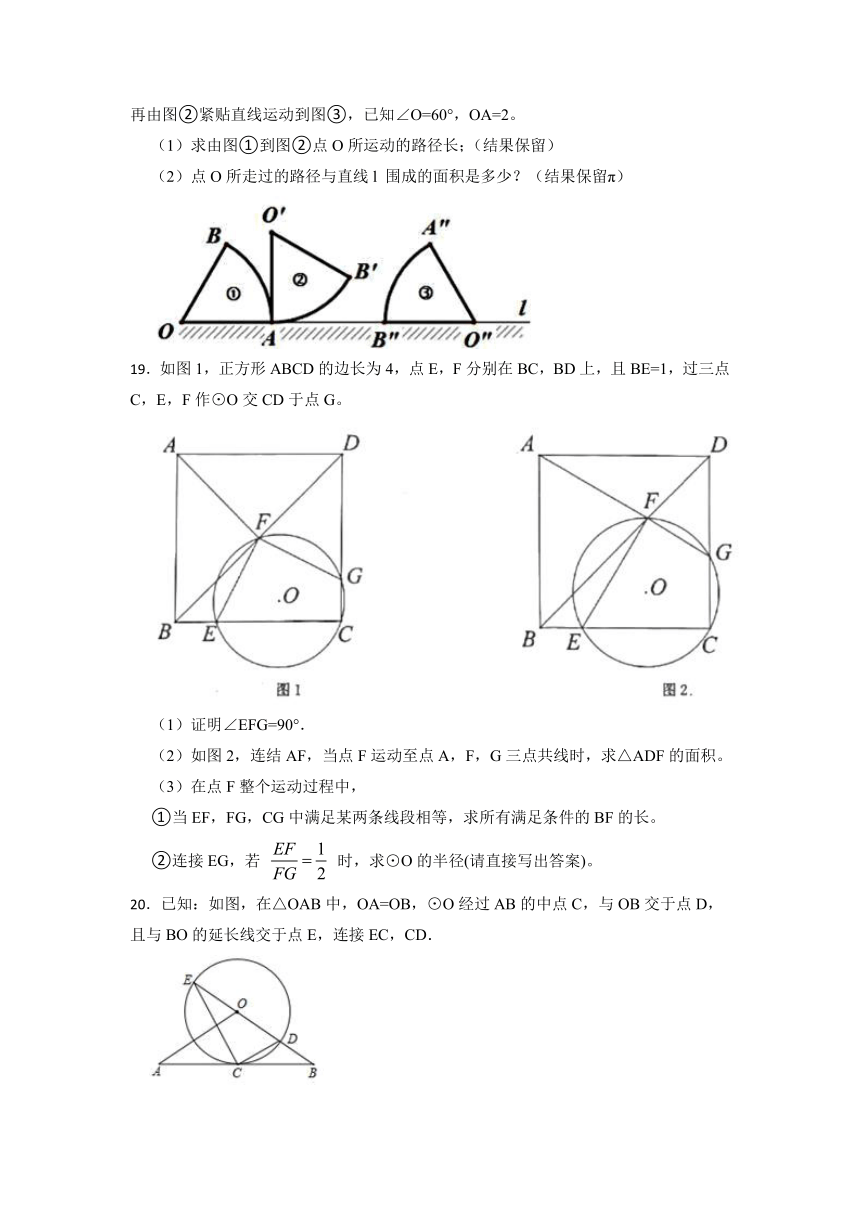
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为 cm.
三、解答题
16.如图,已知△ABC内接于⊙O,AD为直径,点C在劣弧AB上(不与点A,B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:
α 30° 35° 40° 50° 60° 80°
β 120° 125° 130° 140° 150° 170°
猜想:α关于β的函数表达式,并给出证明.
17.如图,某圆形场地内有一个内接于⊙O的正方形中心场地,若⊙O的半径为10米,求图中所画的一块草地的面积.(计算结果保留π)
18.如图所示,扇形OAB从图①无滑动绕着点A旋转到图②(∠O’AO=90°)的位置,再由图②紧贴直线运动到图③,已知∠O=60°,OA=2。
(1)求由图①到图②点O所运动的路径长;(结果保留)
(2)点O所走过的路径与直线l 围成的面积是多少?(结果保留π)
19.如图1,正方形ABCD的边长为4,点E,F分别在BC,BD上,且BE=1,过三点C,E,F作⊙O交CD于点G。
(1)证明∠EFG=90°.
(2)如图2,连结AF,当点F运动至点A,F,G三点共线时,求△ADF的面积。
(3)在点F整个运动过程中,
①当EF,FG,CG中满足某两条线段相等,求所有满足条件的BF的长。
②连接EG,若 时,求⊙O的半径(请直接写出答案)。
20.已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE= ,⊙O的半径为3,求OA的长.
四、综合题
21.如图,AB为⊙O的直径,C为⊙O上一点,AD⊥CE,垂足为D,AC平分∠DAB.
(1)求证:CE是⊙O的切线;
(2)若AD=4, ,求AB的长.
答案解析部分
1.【答案】C
【解析】【解答】解:根据弧长公式:l= =3π,
故答案为:C.
【分析】根据弧长计算公式l=即可直接算出答案。
2.【答案】B
【解析】【解答】解:根据题意可知∠C是弧AB所对的圆周角,
故 的度数是2×∠C=70度.
故选B.
【分析】根据圆心角,圆周角的关系即可解答.
3.【答案】B
【解析】【解答】连接OD、OC,
∵AB是直径,AB=6
∴∠ACB=90°,OD=OC=3
∵CE=BC,
∴∠DBC=∠CEB==45°,
∵
∴∠DOC=2∠DBC=2×45°=90°,
∴△ODC是等腰直角三角形,
∴S阴影=S扇形DOC S△ODC=
故答案为:B
【分析】连接OD、OC,利用圆周角定理可证∠ACB=90°,根据CE=BC,可证得∠DBC=∠CEB=45°,进而得出∠DOC=90°,然后根据S阴影=S扇形DOC S△ODC即可求求解。
4.【答案】B
【解析】【解答】解:∵∠OCA=50°,OA=OC,
∴∠A=50°,
∴∠BOC=2∠A=100°,
∵AB=4,
∴BO=2,
∴的长为:
故答案为:B.
【分析】由等腰三角形的性质可得∠OCA=∠A=50°,由圆周角定理可得∠BOC=2∠A=100°,然后根据弧长公式进行计算.
5.【答案】C
【解析】【解答】如图,在优弧 上取一点D,连接AD、CD,则四边形ABCD是 内接四边形,
,
,
,
故答案为:C.
【分析】如图,在优弧 上取一点D,连接AD、CD,则四边形ABCD是 内接四边形,可得
,利用圆周角定理即得.
6.【答案】D
【解析】【解答】解:连接AO,OB,过点O作OM⊥AB,
∴∠AOM= ∠AOB,AM=BM= AB,
又∵∠C= ∠AOB,
∴∠AOM=∠C,
∵ , ,AD⊥BC,
∴sin∠AOM=sin∠C= ,
又∵AO=3,
∴AM= AO×sin∠AOM=3× = ,
∴AB=2× = .
故答案为:D.
【分析】连接AO,OB,过点O作OM⊥AB,由等腰三角形的性质可得∠AOM=∠AOB,AM=BM=AB,由圆周角定理可得∠C=∠AOB,推出∠AOM=∠C,然后根据等角的同名三角函数值相等可得sin∠AOM=sin∠C= ,据此即可求出答案.
7.【答案】D
【解析】【解答】解:A、圆的直径是一条线段,而圆的对称轴是一条直线,不符合题意;
B、在同圆或等圆中,相等的圆心角所对的弧相等,不符合题意;
C、平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧,不符合题意;
D、圆中最长的弦是直径,符合题意.
故答案为:D.
【分析】根据圆的定义,弧,弦等的定义对每个选项一一判断即可。
8.【答案】D
【解析】【解答】解:∵OC//BD,
∴∠BDC=∠C=28°,
∴∠BOC=56°,
∵OC//BD,
∴∠B=∠BOC=56°,
∵AB是⊙O的直径,
∵∠ADB=90°,
∴∠A=90°-∠B=90°-56°=34°;
故答案为:D
【分析】证明∠B=∠BOC=56°,再证明∠ADB=90°,即可求出答案。
9.【答案】B
【解析】【解答】解:连接CD,
∵BD是⊙O的直径,
∴∠BCD=90°,
由圆周角定理得:∠BDC=∠BAC,
∴sin∠BDC=,
∵BD=4,
∴BC=3.
故答案为:B.
【分析】连接CD,根据圆周角定理可得∠BCD=90°,∠BDC=∠BAC,然后根据正弦函数的概念进行计算.
10.【答案】D
【解析】【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B= (180°-∠AOB)=30°,
在Rt△AOC中,OC= OA=9,
AC= ,
∴AB=2AC= ,
又∵ = ,
∴走便民路比走观赏路少走 米,
故答案为:D.
【分析】作OC⊥AB于C,由垂径定理可得AC=BC,由等边对等角和三角形内角和定理可得∠A=∠B=(180°-∠AOB),在Rt△AOC中,用勾股定理可求得AC的值,再根据AB=2AC可求得AB的值,用弧长公式l=可求得弧AB的值,再求差即可求解.
11.【答案】
【解析】【解答】解:圆的半径为2,则60°圆心角所对的弧长==.
故答案为:.
【分析】直接根据弧长公式“”列式计算,即可得出结果.
12.【答案】6
【解析】【解答】解:设圆的半径为x,由题意得:
=5π,解得:x=6,故答案为:6.
【分析】设圆的半径为x,根据弧长公式列出方程,求出x的值即可.
13.【答案】
【解析】【解答】∵ 中, , ,
∴ ,
∴
结合题意,得弧 的长为:
故答案为: .
【分析】结合题意,根据直角三角形两锐角互余、含 的直角三角形性质,得 , ;根据补角的性质计算,得 ;再根据弧长公式计算,即可得到答案.
14.【答案】
【解析】【解答】解:过点 分别作 交l于点A,B,C,
∵半圆 ,半圆 ,……半圆 与直线 相切,设半圆 ,半圆 ,……,半圆 的半径分别是 , ,……, ,
.
∵ ,
.
在 中, ,
,
.
在 中, ,
,
.
同理可得 ,
故答案为: .
【分析】根据图形找出规律求解即可。
15.【答案】
【解析】【解答】解:连接OC,如图所示:
∵AB是O的直径,弦CD⊥AB,
∴CE=DE= CD=3cm,
∵弧BC=弧BC, ∠CAB=22.5°
∴∠COE=2∠CAB=45°,
∴△COE为等腰直角三角形,
∴OC= CE= cm,
故答案为: .
【分析】连接OC,利用垂径定理可求出CE的长,利用圆周角定理可求出∠COE的度数;由此可证得△COE是等腰直角三角形,利用解直角三角形求出OC的长.
16.【答案】解:结论是:β﹣α=90°, 证明:连接BD, ∵AD为⊙O的直径, ∴∠DBA=90°, ∵∠DAB=α, ∴∠D=90°﹣α, ∵B、D、A、C四点共圆, ∴∠ACB+∠D=180°, ∵∠ACB=β, ∴90°﹣α+β=180°, ∴β﹣α=90°
【解析】【分析】根据圆周角定理求出∠DA=90°,根据三角形内角和定理求出∠D=90°﹣α,根据圆内接四边形的性质得出∠ACB+∠D=180°,代入后求出即可.
17.【答案】解:连AC,则AC为直径,即AC=20,
∵正方形ABCD中,
AB=BC,∠B=90°,
∴在Rt△ABC中,
AB2+BC2=AC2,
2AB2=202,
∴AB2=200,
= =(25π﹣50)米2.
【解析】【分析】连AC,易证AC是圆的直径,利用勾股定理,在Rt△ABC中,求出AB2,再由,计算可求解。
18.【答案】(1)解:由图①到图②:LO= ×2π
= ×2π×2
=π
(2)解:
答:点O所走过的路径与直线l围成的面积是 π。
【解析】【分析】(1)扇形OAB一共转动了3次,从图①到图②,点O运的的轨迹是一个以A为圆心,OA为半径的四分之一圆弧,从图②开始到图②结束,即从O'A垂直与l旋转到O'B'垂直于l,点O运动的轨迹是一段直线段,长度与弧AB的长度相等,从图②旋转到图③,点O运动的轨迹是一个以B''为圆心,O''B''为半径的四分之一圆弧,把三次运动的轨迹相加即可求出由图①到图③点O所运动的路径长;
(2)点O所走过的路径与直线l围成的面积是一个半圆与长为,宽为2的矩形的面积的和。
19.【答案】(1)证明:连结 EG,
在正方形 ABCD 中,得∠C=90°
∴EG 为⊙O 的直径
∴∠EFG=90°
(2)解:如图,过F点作FN⊥AD,交BC于点M,
∵四边形ABCD为正方形,
∴∠ADF=45°,MN=AD,
∴ND=NF,
∴AN=FM,
∵∠MFG=∠AFN,∠MFG+∠MFE=∠AFN+∠FAN,
∴∠MFE=∠FAN,
∴△AFN≌△FEM(AAS),
∴FN=AM,EM=FN,
设AN=x, 则ND=EM=BM-BE=x-1,
∵AN+ND=4,
∴x+x-1=4,
∴x=,
∴FN=EM=BM-BE=-1=,
∴S△AFD=AD×FN=×4×=3.
(3)①1)如图,当EF=FG时,过F作FH⊥BC,FI⊥CD,
∵∠EFH+∠HFG=∠IFG+∠HFG,
∴∠EFH=∠IFG,
∴△EHF≌△GIF(AAS),
∴FH=FI,
又∵FH=BH,
∴BH=FI=HC=2,
∴BF=BH=2.
2)当CG=EF时,
∵EF=CG,
∴FG∥EC,
∵∠C=90°,
∴∠EFG=90°,∠FEC=90°,
∴四边形FECG为矩形,
又∵EF=BE,
∴BF=BE=.
3)当FG=CG,如图,过F点作FN⊥BC,
∵FG=CG,
∴∠FEG=CEG,
∵∠C=∠EFG=90°,
∴∠FGE=∠CGE,
∴EF=EC=BC-BE=4-1=3,
设EN=x,
则FN=BN=x+1,
∵EF2=FN2+EN2,
∴32=(x+1)2+x2,
解得x=,
则BN=,
BF=EN=.
②如图,作FH⊥EC,FK⊥CD,
△FKG∽△FHE,
∴,
设FH=k, 则FK=2k,
∴BH=FH=k,
∴BC=BH+HC=BH+FK=k+2k=4,
∴k=,
∴CG=CK-KG=k-2(k-1)=2-k=2-=,
∴∴EG=,
∴r=.
【解析】【分析】(1) 连结 EG,由90°的圆周角所对的弦为直径,可知EG为圆O的直径,于是根据直径所对的圆周角是直角可得∠EFG=90° .
(2)如图,过F点作FN⊥AD,交BC于点M,利用正方形的性质,结合等角的余角相等,用角角边定理证明△AFN≌△FEN,∴FN=AM,EM=FN,设AN=x, 把ND用含x的代数式表示,根据AN+ND=4,求出x, 则FN可求,于是可求△ADF的面积.
(3) ① 分三种情况讨论,1)当EF=FG时,过F作FH⊥BC,FI⊥CD,利用角角边定理证明△EHF≌△GIF,则对应边FH=FI,BH=FI=HC=2, 于是BF的长度可求;当CG=EF时,易证四边形FECG为矩形,则BF=2BE;当FG=CG,过F点作FN⊥BC,根据同弧所对圆周角相等推得EF=EC,从而求出EF的长,于是利用勾股定理求出FN的长,则BF的长可求.
② 设FH=k, 根据相似的性质,把相关线段用含x的代数式表示,得出BC=k+2k=4, 求出k值,则CG的长度可求,从而利用勾股定理求出直径,则半径可知.
20.【答案】(1)AB与⊙O的位置关系是相切,
证明:如图,连接OC.
∵OA=OB,C为AB的中点,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)∵ED是直径,
∴∠ECD=90°.
∴∠E+∠ODC=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴ .
∴BC2=BD BE.
∵ ,
∴ .
∴ .
设BD=x,则BC=2x.
又BC2=BD BE,
∴(2x)2=x(x+6).
解得x1=0,x2=2.
∵BD=x>0,
∴BD=2.
∴OA=OB=BD+OD=2+3=5.
【解析】【分析】(1) AB与⊙O的位置关系是相切 ,理由如下: 连接OC,根据等腰三角形的三线合一得出 OC⊥AB ,故 AB是⊙O的切线;
(2)首先判断出 ED是直径, 根据直径所对的圆周角是直角得出 ∠ECD=90°,根据等角的余角相等得出 ∠BCD=∠E ,从而判断出 △BCD∽△BEC,根据相似三角形对应边成比例得出 ,根据正切函数的定义得出 , 故 , 设BD=x,则BC=2x,根据比例式建立方程,求解并检验即可算出x的值,从而得出BD的长,然后根据 OA=OB=BD+OD 即可算出答案。
21.【答案】(1)证明:如图,连接 .
∵OA=OC
∴∠OAC=∠OCA
∵∠OAC=∠DAC
∴∠DAC=∠OCA
∵AD⊥CE
∴
∴ ·
即
∵C为⊙O上一点
∴CE是 的切线·
(2)解:如图,连接 .
∵AB是 的直径,
,
,
∵∠BAC=∠CAD
∴△CDA∽△BCA
∴
∴AC=
AB= .
【解析】【分析】(1)先求出∠OAC=∠OCA,再求出 ,最后证明求解即可;
(2)利用相似三角形的判定与性质,再利用锐角三角函数计算求解即可。
一、单选题
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π
2.如图,已知点 、 、 都在 上, ,则 的度数是( )
A. B. C. D.
3.已知,如图,点 C、D 在⊙O 上,直径 AB=6 cm,弦 AC,BD 相交于点 E.若 CE=BC, 则阴影部分面积为( )
A.p - B. p -
C. p - D. p -
4.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
5.如图, 为 的外接圆,已知 为130°,则 的度数为( )
A.50° B.80° C.100° D.115°
6.如图,⊙O的半径为3, 是⊙O的内接三角形,过点A作AD垂直BC于点D.若 , ,则 长是( )
A. B.4 C. D.
7.下列说法正确的是( )
A.圆的任意一条直径都是它的对称轴
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆中最长的弦是直径
8.如图,AB是⊙O的直径,点C、D在圆O上,且OC DB,连接AD、CD,若∠C=28°,则∠A的大小为( )
A.30° B.28° C.24° D.34°
9.如图,⊙O是△ABC的外接圆,直径BD长为4,sin∠BAC=,则BC的长为( )
A. B.3 C. D.
10.如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米.
A. B. C. D.
二、填空题
11.已知圆的半径为2,则60°圆心角所对的弧长为 .
12. 150°的圆心角所对的弧长是5πcm,则此弧所在圆的半径是 cm.
13.如图,在 中, , , ,以 为圆心, 为半径画弧交 的延长线与点 ,则弧 的长为 .
14.如图,圆心都在 轴正半轴上的半圆 ,半圆 ,……半圆 与直线l相切.设半圆 ,半圆 ,……,半圆 的半径分别是 , ,……, ,则当直线l与x轴所成锐角为 ,且 时, .
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为 cm.
三、解答题
16.如图,已知△ABC内接于⊙O,AD为直径,点C在劣弧AB上(不与点A,B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:
α 30° 35° 40° 50° 60° 80°
β 120° 125° 130° 140° 150° 170°
猜想:α关于β的函数表达式,并给出证明.
17.如图,某圆形场地内有一个内接于⊙O的正方形中心场地,若⊙O的半径为10米,求图中所画的一块草地的面积.(计算结果保留π)
18.如图所示,扇形OAB从图①无滑动绕着点A旋转到图②(∠O’AO=90°)的位置,再由图②紧贴直线运动到图③,已知∠O=60°,OA=2。
(1)求由图①到图②点O所运动的路径长;(结果保留)
(2)点O所走过的路径与直线l 围成的面积是多少?(结果保留π)
19.如图1,正方形ABCD的边长为4,点E,F分别在BC,BD上,且BE=1,过三点C,E,F作⊙O交CD于点G。
(1)证明∠EFG=90°.
(2)如图2,连结AF,当点F运动至点A,F,G三点共线时,求△ADF的面积。
(3)在点F整个运动过程中,
①当EF,FG,CG中满足某两条线段相等,求所有满足条件的BF的长。
②连接EG,若 时,求⊙O的半径(请直接写出答案)。
20.已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE= ,⊙O的半径为3,求OA的长.
四、综合题
21.如图,AB为⊙O的直径,C为⊙O上一点,AD⊥CE,垂足为D,AC平分∠DAB.
(1)求证:CE是⊙O的切线;
(2)若AD=4, ,求AB的长.
答案解析部分
1.【答案】C
【解析】【解答】解:根据弧长公式:l= =3π,
故答案为:C.
【分析】根据弧长计算公式l=即可直接算出答案。
2.【答案】B
【解析】【解答】解:根据题意可知∠C是弧AB所对的圆周角,
故 的度数是2×∠C=70度.
故选B.
【分析】根据圆心角,圆周角的关系即可解答.
3.【答案】B
【解析】【解答】连接OD、OC,
∵AB是直径,AB=6
∴∠ACB=90°,OD=OC=3
∵CE=BC,
∴∠DBC=∠CEB==45°,
∵
∴∠DOC=2∠DBC=2×45°=90°,
∴△ODC是等腰直角三角形,
∴S阴影=S扇形DOC S△ODC=
故答案为:B
【分析】连接OD、OC,利用圆周角定理可证∠ACB=90°,根据CE=BC,可证得∠DBC=∠CEB=45°,进而得出∠DOC=90°,然后根据S阴影=S扇形DOC S△ODC即可求求解。
4.【答案】B
【解析】【解答】解:∵∠OCA=50°,OA=OC,
∴∠A=50°,
∴∠BOC=2∠A=100°,
∵AB=4,
∴BO=2,
∴的长为:
故答案为:B.
【分析】由等腰三角形的性质可得∠OCA=∠A=50°,由圆周角定理可得∠BOC=2∠A=100°,然后根据弧长公式进行计算.
5.【答案】C
【解析】【解答】如图,在优弧 上取一点D,连接AD、CD,则四边形ABCD是 内接四边形,
,
,
,
故答案为:C.
【分析】如图,在优弧 上取一点D,连接AD、CD,则四边形ABCD是 内接四边形,可得
,利用圆周角定理即得.
6.【答案】D
【解析】【解答】解:连接AO,OB,过点O作OM⊥AB,
∴∠AOM= ∠AOB,AM=BM= AB,
又∵∠C= ∠AOB,
∴∠AOM=∠C,
∵ , ,AD⊥BC,
∴sin∠AOM=sin∠C= ,
又∵AO=3,
∴AM= AO×sin∠AOM=3× = ,
∴AB=2× = .
故答案为:D.
【分析】连接AO,OB,过点O作OM⊥AB,由等腰三角形的性质可得∠AOM=∠AOB,AM=BM=AB,由圆周角定理可得∠C=∠AOB,推出∠AOM=∠C,然后根据等角的同名三角函数值相等可得sin∠AOM=sin∠C= ,据此即可求出答案.
7.【答案】D
【解析】【解答】解:A、圆的直径是一条线段,而圆的对称轴是一条直线,不符合题意;
B、在同圆或等圆中,相等的圆心角所对的弧相等,不符合题意;
C、平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧,不符合题意;
D、圆中最长的弦是直径,符合题意.
故答案为:D.
【分析】根据圆的定义,弧,弦等的定义对每个选项一一判断即可。
8.【答案】D
【解析】【解答】解:∵OC//BD,
∴∠BDC=∠C=28°,
∴∠BOC=56°,
∵OC//BD,
∴∠B=∠BOC=56°,
∵AB是⊙O的直径,
∵∠ADB=90°,
∴∠A=90°-∠B=90°-56°=34°;
故答案为:D
【分析】证明∠B=∠BOC=56°,再证明∠ADB=90°,即可求出答案。
9.【答案】B
【解析】【解答】解:连接CD,
∵BD是⊙O的直径,
∴∠BCD=90°,
由圆周角定理得:∠BDC=∠BAC,
∴sin∠BDC=,
∵BD=4,
∴BC=3.
故答案为:B.
【分析】连接CD,根据圆周角定理可得∠BCD=90°,∠BDC=∠BAC,然后根据正弦函数的概念进行计算.
10.【答案】D
【解析】【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B= (180°-∠AOB)=30°,
在Rt△AOC中,OC= OA=9,
AC= ,
∴AB=2AC= ,
又∵ = ,
∴走便民路比走观赏路少走 米,
故答案为:D.
【分析】作OC⊥AB于C,由垂径定理可得AC=BC,由等边对等角和三角形内角和定理可得∠A=∠B=(180°-∠AOB),在Rt△AOC中,用勾股定理可求得AC的值,再根据AB=2AC可求得AB的值,用弧长公式l=可求得弧AB的值,再求差即可求解.
11.【答案】
【解析】【解答】解:圆的半径为2,则60°圆心角所对的弧长==.
故答案为:.
【分析】直接根据弧长公式“”列式计算,即可得出结果.
12.【答案】6
【解析】【解答】解:设圆的半径为x,由题意得:
=5π,解得:x=6,故答案为:6.
【分析】设圆的半径为x,根据弧长公式列出方程,求出x的值即可.
13.【答案】
【解析】【解答】∵ 中, , ,
∴ ,
∴
结合题意,得弧 的长为:
故答案为: .
【分析】结合题意,根据直角三角形两锐角互余、含 的直角三角形性质,得 , ;根据补角的性质计算,得 ;再根据弧长公式计算,即可得到答案.
14.【答案】
【解析】【解答】解:过点 分别作 交l于点A,B,C,
∵半圆 ,半圆 ,……半圆 与直线 相切,设半圆 ,半圆 ,……,半圆 的半径分别是 , ,……, ,
.
∵ ,
.
在 中, ,
,
.
在 中, ,
,
.
同理可得 ,
故答案为: .
【分析】根据图形找出规律求解即可。
15.【答案】
【解析】【解答】解:连接OC,如图所示:
∵AB是O的直径,弦CD⊥AB,
∴CE=DE= CD=3cm,
∵弧BC=弧BC, ∠CAB=22.5°
∴∠COE=2∠CAB=45°,
∴△COE为等腰直角三角形,
∴OC= CE= cm,
故答案为: .
【分析】连接OC,利用垂径定理可求出CE的长,利用圆周角定理可求出∠COE的度数;由此可证得△COE是等腰直角三角形,利用解直角三角形求出OC的长.
16.【答案】解:结论是:β﹣α=90°, 证明:连接BD, ∵AD为⊙O的直径, ∴∠DBA=90°, ∵∠DAB=α, ∴∠D=90°﹣α, ∵B、D、A、C四点共圆, ∴∠ACB+∠D=180°, ∵∠ACB=β, ∴90°﹣α+β=180°, ∴β﹣α=90°
【解析】【分析】根据圆周角定理求出∠DA=90°,根据三角形内角和定理求出∠D=90°﹣α,根据圆内接四边形的性质得出∠ACB+∠D=180°,代入后求出即可.
17.【答案】解:连AC,则AC为直径,即AC=20,
∵正方形ABCD中,
AB=BC,∠B=90°,
∴在Rt△ABC中,
AB2+BC2=AC2,
2AB2=202,
∴AB2=200,
= =(25π﹣50)米2.
【解析】【分析】连AC,易证AC是圆的直径,利用勾股定理,在Rt△ABC中,求出AB2,再由,计算可求解。
18.【答案】(1)解:由图①到图②:LO= ×2π
= ×2π×2
=π
(2)解:
答:点O所走过的路径与直线l围成的面积是 π。
【解析】【分析】(1)扇形OAB一共转动了3次,从图①到图②,点O运的的轨迹是一个以A为圆心,OA为半径的四分之一圆弧,从图②开始到图②结束,即从O'A垂直与l旋转到O'B'垂直于l,点O运动的轨迹是一段直线段,长度与弧AB的长度相等,从图②旋转到图③,点O运动的轨迹是一个以B''为圆心,O''B''为半径的四分之一圆弧,把三次运动的轨迹相加即可求出由图①到图③点O所运动的路径长;
(2)点O所走过的路径与直线l围成的面积是一个半圆与长为,宽为2的矩形的面积的和。
19.【答案】(1)证明:连结 EG,
在正方形 ABCD 中,得∠C=90°
∴EG 为⊙O 的直径
∴∠EFG=90°
(2)解:如图,过F点作FN⊥AD,交BC于点M,
∵四边形ABCD为正方形,
∴∠ADF=45°,MN=AD,
∴ND=NF,
∴AN=FM,
∵∠MFG=∠AFN,∠MFG+∠MFE=∠AFN+∠FAN,
∴∠MFE=∠FAN,
∴△AFN≌△FEM(AAS),
∴FN=AM,EM=FN,
设AN=x, 则ND=EM=BM-BE=x-1,
∵AN+ND=4,
∴x+x-1=4,
∴x=,
∴FN=EM=BM-BE=-1=,
∴S△AFD=AD×FN=×4×=3.
(3)①1)如图,当EF=FG时,过F作FH⊥BC,FI⊥CD,
∵∠EFH+∠HFG=∠IFG+∠HFG,
∴∠EFH=∠IFG,
∴△EHF≌△GIF(AAS),
∴FH=FI,
又∵FH=BH,
∴BH=FI=HC=2,
∴BF=BH=2.
2)当CG=EF时,
∵EF=CG,
∴FG∥EC,
∵∠C=90°,
∴∠EFG=90°,∠FEC=90°,
∴四边形FECG为矩形,
又∵EF=BE,
∴BF=BE=.
3)当FG=CG,如图,过F点作FN⊥BC,
∵FG=CG,
∴∠FEG=CEG,
∵∠C=∠EFG=90°,
∴∠FGE=∠CGE,
∴EF=EC=BC-BE=4-1=3,
设EN=x,
则FN=BN=x+1,
∵EF2=FN2+EN2,
∴32=(x+1)2+x2,
解得x=,
则BN=,
BF=EN=.
②如图,作FH⊥EC,FK⊥CD,
△FKG∽△FHE,
∴,
设FH=k, 则FK=2k,
∴BH=FH=k,
∴BC=BH+HC=BH+FK=k+2k=4,
∴k=,
∴CG=CK-KG=k-2(k-1)=2-k=2-=,
∴∴EG=,
∴r=.
【解析】【分析】(1) 连结 EG,由90°的圆周角所对的弦为直径,可知EG为圆O的直径,于是根据直径所对的圆周角是直角可得∠EFG=90° .
(2)如图,过F点作FN⊥AD,交BC于点M,利用正方形的性质,结合等角的余角相等,用角角边定理证明△AFN≌△FEN,∴FN=AM,EM=FN,设AN=x, 把ND用含x的代数式表示,根据AN+ND=4,求出x, 则FN可求,于是可求△ADF的面积.
(3) ① 分三种情况讨论,1)当EF=FG时,过F作FH⊥BC,FI⊥CD,利用角角边定理证明△EHF≌△GIF,则对应边FH=FI,BH=FI=HC=2, 于是BF的长度可求;当CG=EF时,易证四边形FECG为矩形,则BF=2BE;当FG=CG,过F点作FN⊥BC,根据同弧所对圆周角相等推得EF=EC,从而求出EF的长,于是利用勾股定理求出FN的长,则BF的长可求.
② 设FH=k, 根据相似的性质,把相关线段用含x的代数式表示,得出BC=k+2k=4, 求出k值,则CG的长度可求,从而利用勾股定理求出直径,则半径可知.
20.【答案】(1)AB与⊙O的位置关系是相切,
证明:如图,连接OC.
∵OA=OB,C为AB的中点,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)∵ED是直径,
∴∠ECD=90°.
∴∠E+∠ODC=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴ .
∴BC2=BD BE.
∵ ,
∴ .
∴ .
设BD=x,则BC=2x.
又BC2=BD BE,
∴(2x)2=x(x+6).
解得x1=0,x2=2.
∵BD=x>0,
∴BD=2.
∴OA=OB=BD+OD=2+3=5.
【解析】【分析】(1) AB与⊙O的位置关系是相切 ,理由如下: 连接OC,根据等腰三角形的三线合一得出 OC⊥AB ,故 AB是⊙O的切线;
(2)首先判断出 ED是直径, 根据直径所对的圆周角是直角得出 ∠ECD=90°,根据等角的余角相等得出 ∠BCD=∠E ,从而判断出 △BCD∽△BEC,根据相似三角形对应边成比例得出 ,根据正切函数的定义得出 , 故 , 设BD=x,则BC=2x,根据比例式建立方程,求解并检验即可算出x的值,从而得出BD的长,然后根据 OA=OB=BD+OD 即可算出答案。
21.【答案】(1)证明:如图,连接 .
∵OA=OC
∴∠OAC=∠OCA
∵∠OAC=∠DAC
∴∠DAC=∠OCA
∵AD⊥CE
∴
∴ ·
即
∵C为⊙O上一点
∴CE是 的切线·
(2)解:如图,连接 .
∵AB是 的直径,
,
,
∵∠BAC=∠CAD
∴△CDA∽△BCA
∴
∴AC=
AB= .
【解析】【分析】(1)先求出∠OAC=∠OCA,再求出 ,最后证明求解即可;
(2)利用相似三角形的判定与性质,再利用锐角三角函数计算求解即可。
