9.2用样本的数字特征估计总体的数字特征 课件(共21张PPT)
文档属性
| 名称 | 9.2用样本的数字特征估计总体的数字特征 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 788.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
2.2用样本估计总体
求职者小杨
这个公司员工收入到底怎样?
易经理
我这里报酬不错, 月平均工资是4000元,你在这里好好干!
我们公司的平均工资是4000元,你在这里好好干!
王经理
求职者小杨
这个公司员工收入到底怎样?
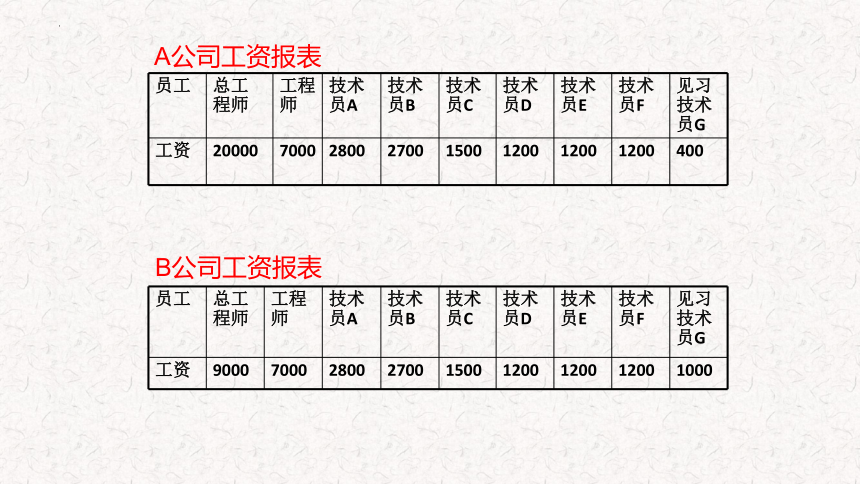
员工 总工程师 工程师 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 见习技术员G
工资 20000 7000 2800 2700 1500 1200 1200 1200 400
员工 总工程师 工程师 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 见习技术员G
工资 9000 7000 2800 2700 1500 1200 1200 1200 1000
A公司工资报表
B公司工资报表
2.2.2用样本的数字特征估计总体的数字特征
学习目标:
1.会求样本的众数、中位数、平均数、标准差、方差;
2.理解用样本的数字特征来估计总体数字特征的方法;
3.会应用相关知识解决简单的统计实际问题。
1.求下列各组数据的众数
(1)1 ,2,3,3,3,5,5,8,8,8,9,9
众数是:3和8
(2)1 ,2,3,3,3,5,5,8,8,9,9
众数是:3
(1)1 ,2,3,3,3,4,6,8,8,8,9,9
(2)1 ,2,3,3,3,4,8,8,8,9,9
中位数是:5
中位数是:4
2.求下列各组数据的中位数
基础回顾
3.在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数,中位数与平均数 。
解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;
答:17名运动员成绩的众数、中位数、平均数依次是1.75(米)、1.70(米)、1.69(米)。
这组数据的平均数是
1.众数:在一组数据中,出现次数最多的数据叫做这组数据的众数;
2.中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数;
3.平均数:样本数据的算术平均值,即
归纳总结:
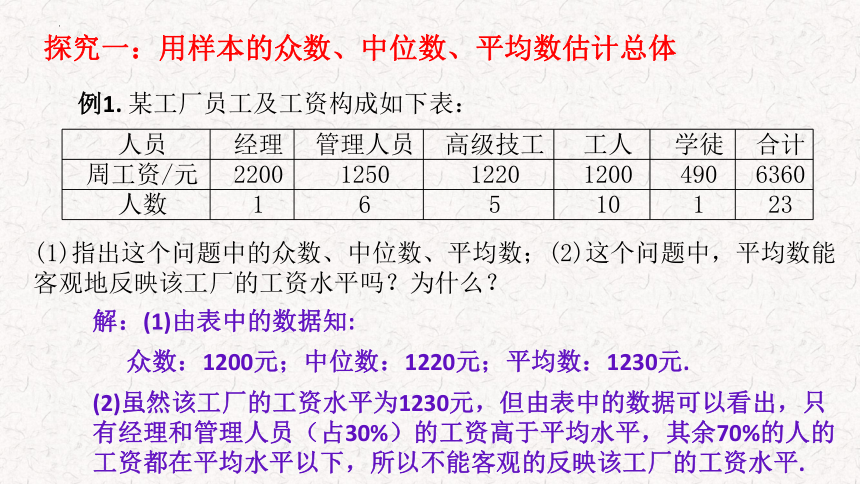
人员 经理 管理人员 高级技工 工人 学徒 合计
周工资/元 2200 1250 1220 1200 490 6360
人数 1 6 5 10 1 23
(1)指出这个问题中的众数、中位数、平均数;(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?
探究一:用样本的众数、中位数、平均数估计总体
解:(1)由表中的数据知:
众数:1200元;中位数:1220元;平均数:1230元.
(2)虽然该工厂的工资水平为1230元,但由表中的数据可以看出,只有经理和管理人员(占30%)的工资高于平均水平,其余70%的人的工资都在平均水平以下,所以不能客观的反映该工厂的工资水平.
例1. 某工厂员工及工资构成如下表:
总结:三种数字特征的优缺点
特征数 优点 缺点
众数 体现了样本数据的最大集中点 对其他数据信息的忽视,使得无法客观的反映总体的特征
中位数 是样本数据的所占频率的等分线,不受少数极端值得影响 对极端值不敏感
平均数 与每一个数据有关,更能反映全体的信息 受少数极端值的影响较大,使其在估计总体时的可靠性降低
变式训练1:某工厂随机抽取20名工人年龄数据如下表:
年龄(岁) 工人数(人)
19 1
28 3
29 3
30 5
31 4
32 3
40 1
合计 20
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)计算20名工人年龄的平均年龄,并估计这个工厂员工的平均年龄.
甲、乙两台机床同时加工直径为100 mm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
计算这两组数据的平均数,然后判断哪台机床加工的零件质量更稳定.
探究二
探究二:用样本标准差估计总体标准差
数据的离散程度可以用极差、方差或标准差来描述.我们知道,样本方差描述了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常要求计算出样本方差的算术平方根,即标准差。
1.定义:一般设样本的元素为 ,样本的平均数为 ,定义
其中 表示样本方差, 表示样本标准差.
注:(1)一组数据的方差或标准差越大,说明这组数据波动越大,越不稳定.
(2) 计算标准差的算法.
例2.甲、乙两台机床同时加工直径为100 mm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及标准差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
变式训练2:从甲、乙两种玉米苗中各抽10株,分别测得它们的株高如下:(单位:cm)
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
根据以上数据回答下列问题.
(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
探究三:方差的运算性质
例3.(1)在例2中,若甲机床所加工的6个零件的数据全都加10,那么所得新数据的平均数及方差分别是多少
(2)1,3,5,7的平均数为 方差为
(3)2,6,10,14的平均数为 方差为
(4)3,7,11,15的平均数为 方差为
规律总结:方差的运算性质
如果数据 的平均数为 ,方差为 ,则:
(1)新数据 的平均数为 ,方差为 .
(2)新数据 的平均数为 ,方差为 .
(3)新数据 的平均数为 ,方差为 .
(1)若 的方差为4,那么
的方差为 .
(2)若 的方差为2,那么这组数据均乘以4
后的方差为 .
变式训练3:
(1)用众数、中位数、平均数估计总体;
(2)用样本的标准差估计总体的标准差;
归纳小结
通过本节课的学习,你有哪些收获?
1.知识方面
2.思想方法
归纳
(3)方差运算的性质。
谢谢各位老师及同学!
2.2用样本估计总体
求职者小杨
这个公司员工收入到底怎样?
易经理
我这里报酬不错, 月平均工资是4000元,你在这里好好干!
我们公司的平均工资是4000元,你在这里好好干!
王经理
求职者小杨
这个公司员工收入到底怎样?
员工 总工程师 工程师 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 见习技术员G
工资 20000 7000 2800 2700 1500 1200 1200 1200 400
员工 总工程师 工程师 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 见习技术员G
工资 9000 7000 2800 2700 1500 1200 1200 1200 1000
A公司工资报表
B公司工资报表
2.2.2用样本的数字特征估计总体的数字特征
学习目标:
1.会求样本的众数、中位数、平均数、标准差、方差;
2.理解用样本的数字特征来估计总体数字特征的方法;
3.会应用相关知识解决简单的统计实际问题。
1.求下列各组数据的众数
(1)1 ,2,3,3,3,5,5,8,8,8,9,9
众数是:3和8
(2)1 ,2,3,3,3,5,5,8,8,9,9
众数是:3
(1)1 ,2,3,3,3,4,6,8,8,8,9,9
(2)1 ,2,3,3,3,4,8,8,8,9,9
中位数是:5
中位数是:4
2.求下列各组数据的中位数
基础回顾
3.在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数,中位数与平均数 。
解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;
答:17名运动员成绩的众数、中位数、平均数依次是1.75(米)、1.70(米)、1.69(米)。
这组数据的平均数是
1.众数:在一组数据中,出现次数最多的数据叫做这组数据的众数;
2.中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数;
3.平均数:样本数据的算术平均值,即
归纳总结:
人员 经理 管理人员 高级技工 工人 学徒 合计
周工资/元 2200 1250 1220 1200 490 6360
人数 1 6 5 10 1 23
(1)指出这个问题中的众数、中位数、平均数;(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?
探究一:用样本的众数、中位数、平均数估计总体
解:(1)由表中的数据知:
众数:1200元;中位数:1220元;平均数:1230元.
(2)虽然该工厂的工资水平为1230元,但由表中的数据可以看出,只有经理和管理人员(占30%)的工资高于平均水平,其余70%的人的工资都在平均水平以下,所以不能客观的反映该工厂的工资水平.
例1. 某工厂员工及工资构成如下表:
总结:三种数字特征的优缺点
特征数 优点 缺点
众数 体现了样本数据的最大集中点 对其他数据信息的忽视,使得无法客观的反映总体的特征
中位数 是样本数据的所占频率的等分线,不受少数极端值得影响 对极端值不敏感
平均数 与每一个数据有关,更能反映全体的信息 受少数极端值的影响较大,使其在估计总体时的可靠性降低
变式训练1:某工厂随机抽取20名工人年龄数据如下表:
年龄(岁) 工人数(人)
19 1
28 3
29 3
30 5
31 4
32 3
40 1
合计 20
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)计算20名工人年龄的平均年龄,并估计这个工厂员工的平均年龄.
甲、乙两台机床同时加工直径为100 mm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
计算这两组数据的平均数,然后判断哪台机床加工的零件质量更稳定.
探究二
探究二:用样本标准差估计总体标准差
数据的离散程度可以用极差、方差或标准差来描述.我们知道,样本方差描述了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常要求计算出样本方差的算术平方根,即标准差。
1.定义:一般设样本的元素为 ,样本的平均数为 ,定义
其中 表示样本方差, 表示样本标准差.
注:(1)一组数据的方差或标准差越大,说明这组数据波动越大,越不稳定.
(2) 计算标准差的算法.
例2.甲、乙两台机床同时加工直径为100 mm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及标准差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
变式训练2:从甲、乙两种玉米苗中各抽10株,分别测得它们的株高如下:(单位:cm)
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
根据以上数据回答下列问题.
(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
探究三:方差的运算性质
例3.(1)在例2中,若甲机床所加工的6个零件的数据全都加10,那么所得新数据的平均数及方差分别是多少
(2)1,3,5,7的平均数为 方差为
(3)2,6,10,14的平均数为 方差为
(4)3,7,11,15的平均数为 方差为
规律总结:方差的运算性质
如果数据 的平均数为 ,方差为 ,则:
(1)新数据 的平均数为 ,方差为 .
(2)新数据 的平均数为 ,方差为 .
(3)新数据 的平均数为 ,方差为 .
(1)若 的方差为4,那么
的方差为 .
(2)若 的方差为2,那么这组数据均乘以4
后的方差为 .
变式训练3:
(1)用众数、中位数、平均数估计总体;
(2)用样本的标准差估计总体的标准差;
归纳小结
通过本节课的学习,你有哪些收获?
1.知识方面
2.思想方法
归纳
(3)方差运算的性质。
谢谢各位老师及同学!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
