6.1平行四边形的性质 课件

课件21张PPT。平行四边形的性质一、创设情境、引入课题 爱动脑筋的小明观察到平行四边形影子有一种对称的美，他说只要量出一个内角的度数，就能知道其余三个内角的度数，只需测出一组相邻的边长，便能计算出它的周长，这是为什么？　1．在对平行四边形认识的基础上，探索并
掌握平行四边形的性质；
　2．会利用平行四边形的性质去解决实际
问题。学习目标学习重点：理解并正确运用平行四边形的
性质.
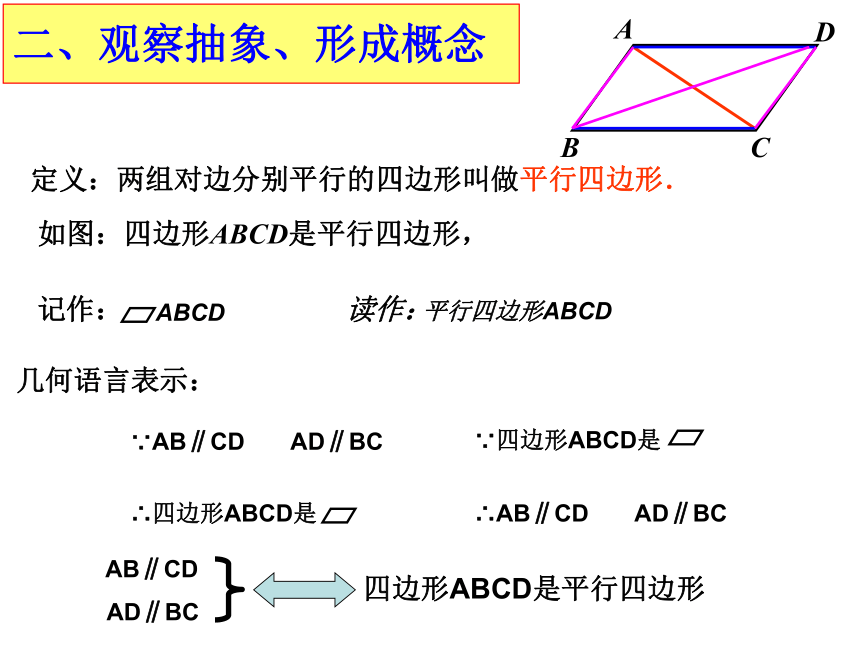
学习难点：平行四边形的性质的探索.生活中的图形二、观察抽象、形成概念定义：两组对边分别平行的四边形叫做平行四边形．如图：四边形ABCD是平行四边形，
记作： 读作：几何语言表示：四边形ABCD是平行四边形ABCD平行四边形ABCD∵AB∥CD AD∥BC∴AB∥CD AD∥BC AB∥CD
AD∥BC三、自主探究、学习新知 1、用两个全等的三角形纸片可以拼出多少种形状不同的平行四边形？从拼图可以得到什么启示？拼一拼 2、你能发现平行四边形的边、角关系吗？
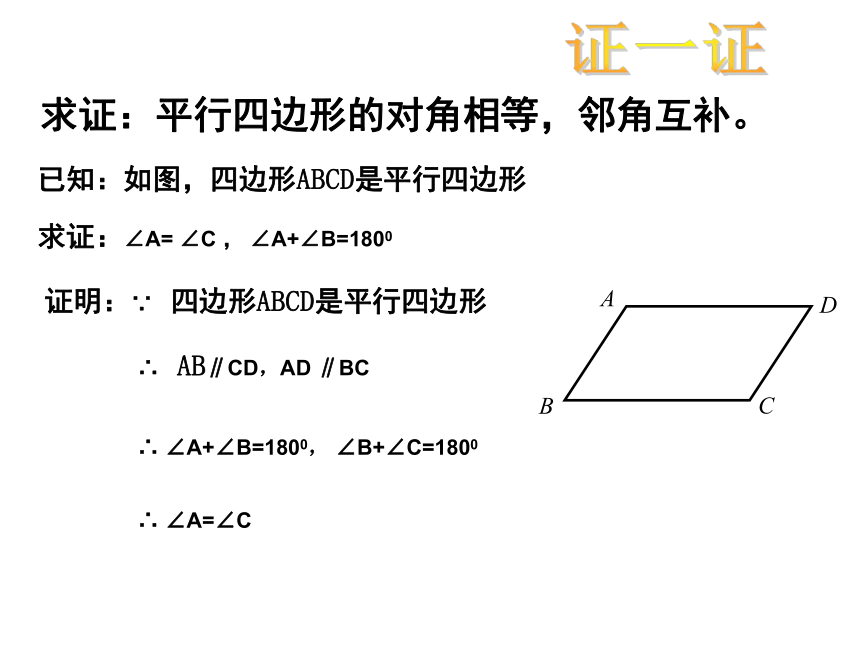
你是怎么发现的？证一证 求证：平行四边形的对角相等，邻角互补。 已知：如图，四边形ABCD是平行四边形求证：∠A= ∠C ， ∠A+∠B=1800 证明：∵ 四边形ABCD是平行四边形∴ AB∥CD，AD ∥BC∴ ∠A+∠B=1800， ∠B+∠C=1800∴ ∠A=∠C证一证 求证：平行四边形的对边相等。 已知：如图，四边形ABCD是平行四边形求证：AB= CD ， AD=BC证明：连接AC ∵ 四边形ABCD是平行四边形∴ AD ∥BC， AB∥CD∴ ∠1= ∠2， ∠3= ∠41234 ∵ AC=CA∴ △ABC≌ △CDA（ASA）∴AB= CD ， AD=BC方法归纳：平行四边形问题
常转化为三角形问题。 如图，把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉，将一个平行四边形绕O旋转180°，你发现了什么? 试一试看一看归纳平行四边形的性质：ABCD2、平行四边形的对边相等．1、平行四边形的对角相等、邻角互补．3、平行四边形是中心对称图形，两条
对角线的交点是它们的对称中心．你能回答小明的问题吗？ 爱动脑筋的小明观察到平行四边形影子有一种对称的美，他说只要量出一个内角的度数，就能知道其余三个内角的度数，只需测出一组相邻的边长，便能计算出它的周长，这是为什么？四、初步应用、体验成功变题1、 的周长是20，已知AB＝6，则BC＝＿＿，CD＝＿＿.与小明一起玩游戏ABCDEFGH已知： AB ∥CD ∥EF ， AE∥GH ∥BF4030120°120°60°120°40°五、学以致用、强化新知3、如图，已知□ABCD中，AB=４,BC=3，CD= ；AD= ；□ABCD周长　 ．4、如图，在□ABCD中，AC为对角线，BE⊥AC， DF⊥AC，
E、F为垂足， 求证：BE＝DF．六、归纳总结、布置作业这节课我们一起探究了哪些知识？同学们收获了什么？①平行四边形的定义与性质；②转化与分类讨论的数学思想；③证明平行、线段相等、角相等的新方法。谢谢倾听

敬请指导！3：如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F.
求证：∠BAE＝∠DCF。