2.1.1第一课时 等式性质与不等式性质(1)--高一年级数学人教版(2019)必修一 课件(共28张PPT)
文档属性
| 名称 | 2.1.1第一课时 等式性质与不等式性质(1)--高一年级数学人教版(2019)必修一 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
新教材人教版·高中必修第一册
数学
2.1等式性质与不等式性质(1)
第一课时 不等关系与不等式
第二章 一元二次函数、方程和不等式
要求
课标要求
1.通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系.
2.了解不等式(组)的实际背景.
素养要求
通过运用不等式(组)表示实际问题的不等关系及比较两个实数的大小提升数学抽象及数学运算素养.
复习引入
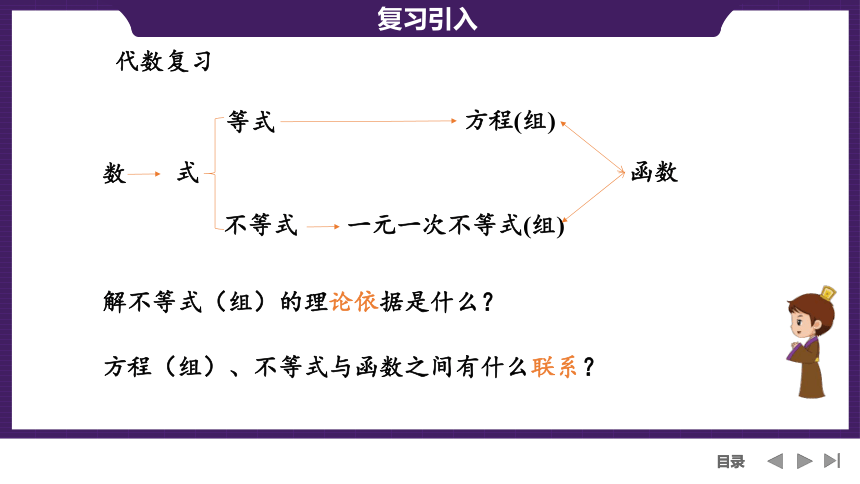
代数复习
数
式
等式
不等式
方程(组)
一元一次不等式(组)
函数
解不等式(组)的理论依据是什么?
方程(组)、不等式与函数之间有什么联系?
复习引入
常见的不等关系有哪些?你能用文字语言和符号语言表述吗?
文字语言 符号语言
大于 >
小于 <
大于或等于(不小于) ≥
小于或等于(不大于) ≤
复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速40 km/h;
问题1
解:
设在该路段行驶的汽车的速度为vkm/h,“限速40 km/h”就是v的大小不能超过40,于是0复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%;
问题1
解:
复习引入
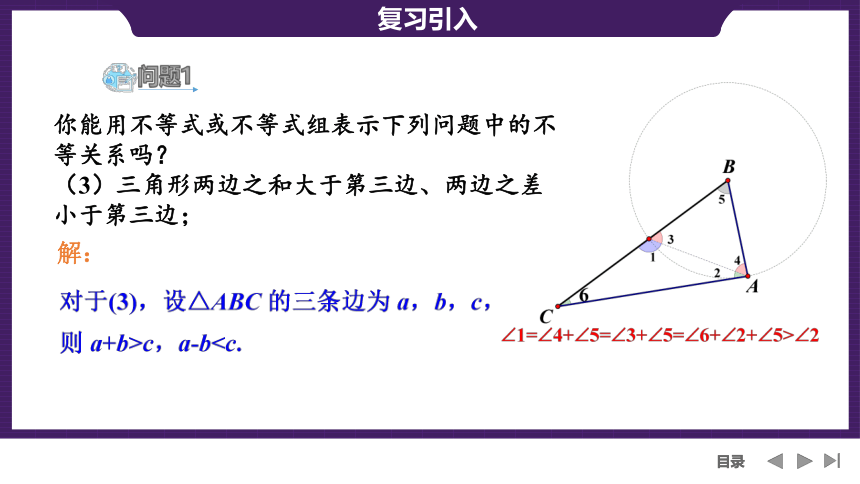
你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边、两边之差小于第三边;
问题1
解:
复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
问题1
解:
复习引入
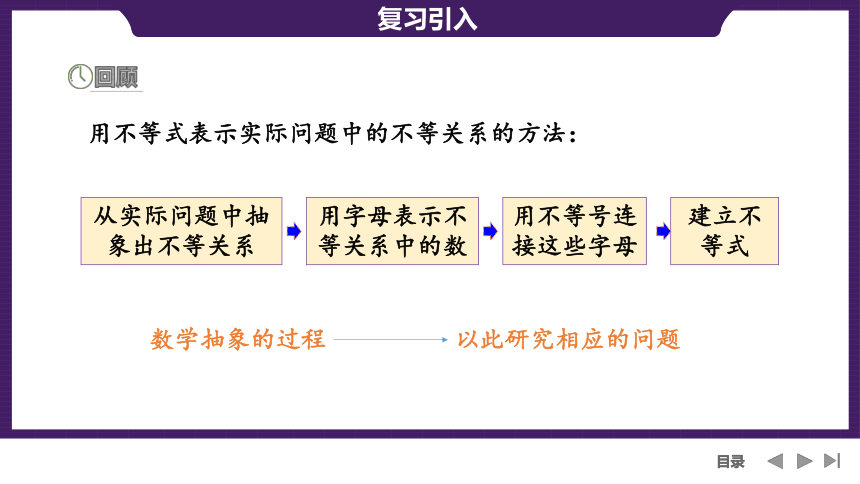
回顾
从实际问题中抽
象出不等关系
用字母表示不等关系中的数
用不等号连接这些字母
建立不等式
数学抽象的过程
以此研究相应的问题
用不等式表示实际问题中的不等关系的方法:
新知引入
问题2
如何解这个不等式?
新知引入
类比
类比
概念引入
A a B b
概念引入
概念理解
运算
作差法:比较两个实数(式子)大小关系的方法.
巩固与练习(1)
温馨提示
0是正数与负数的分界点,它为实数比较大小提供了“标杆”
巩固与练习(1)
思维升华
巩固与练习(2)
巩固与练习(2)
追问1
巩固与练习(2)
追问2
巩固与练习(2)
追问3
巩固与练习(2)
思维升华
巩固与练习(3)
深化与思考
深化
深化与思考
思考辨析
×
√
×
小结
限时小练
简解答:
课堂作业
1、练习1,2,3
2、预习 本节剩余部分。
本节内容结束
THANKS
新教材人教版·高中必修第一册
数学
2.1等式性质与不等式性质(1)
第一课时 不等关系与不等式
第二章 一元二次函数、方程和不等式
要求
课标要求
1.通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系.
2.了解不等式(组)的实际背景.
素养要求
通过运用不等式(组)表示实际问题的不等关系及比较两个实数的大小提升数学抽象及数学运算素养.
复习引入
代数复习
数
式
等式
不等式
方程(组)
一元一次不等式(组)
函数
解不等式(组)的理论依据是什么?
方程(组)、不等式与函数之间有什么联系?
复习引入
常见的不等关系有哪些?你能用文字语言和符号语言表述吗?
文字语言 符号语言
大于 >
小于 <
大于或等于(不小于) ≥
小于或等于(不大于) ≤
复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速40 km/h;
问题1
解:
设在该路段行驶的汽车的速度为vkm/h,“限速40 km/h”就是v的大小不能超过40,于是0
你能用不等式或不等式组表示下列问题中的不等关系吗?
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%;
问题1
解:
复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边、两边之差小于第三边;
问题1
解:
复习引入
你能用不等式或不等式组表示下列问题中的不等关系吗?
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
问题1
解:
复习引入
回顾
从实际问题中抽
象出不等关系
用字母表示不等关系中的数
用不等号连接这些字母
建立不等式
数学抽象的过程
以此研究相应的问题
用不等式表示实际问题中的不等关系的方法:
新知引入
问题2
如何解这个不等式?
新知引入
类比
类比
概念引入
A a B b
概念引入
概念理解
运算
作差法:比较两个实数(式子)大小关系的方法.
巩固与练习(1)
温馨提示
0是正数与负数的分界点,它为实数比较大小提供了“标杆”
巩固与练习(1)
思维升华
巩固与练习(2)
巩固与练习(2)
追问1
巩固与练习(2)
追问2
巩固与练习(2)
追问3
巩固与练习(2)
思维升华
巩固与练习(3)
深化与思考
深化
深化与思考
思考辨析
×
√
×
小结
限时小练
简解答:
课堂作业
1、练习1,2,3
2、预习 本节剩余部分。
本节内容结束
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
