2.1.2第二课时 等式性质与不等式性质(2)--高一年级数学人教版(2019)必修一 课件(共23张PPT)
文档属性
| 名称 | 2.1.2第二课时 等式性质与不等式性质(2)--高一年级数学人教版(2019)必修一 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
新教材人教版·高中必修第一册
数学
2.1等式性质与不等式性质(2)
第二课时 不等式的性质
第二章 一元二次函数、方程和不等式
要求
课标要求
1.掌握不等式的基本性质.
2.运用不等式的性质解决有关问题.
素养要求
通过学习不等式的性质及运用不等式的性质解决问题,提升数学抽象、逻辑推理及数学运算素养.
复习引入
请你回忆一下,等式都有哪些性质?
问题1
性质1:如果a=b,那么b=a.
性质2:如果a=b,b=c,那么a=C.
自身特性
对称性
传递性
复习引入
请你回忆一下,等式都有哪些性质?
问题1
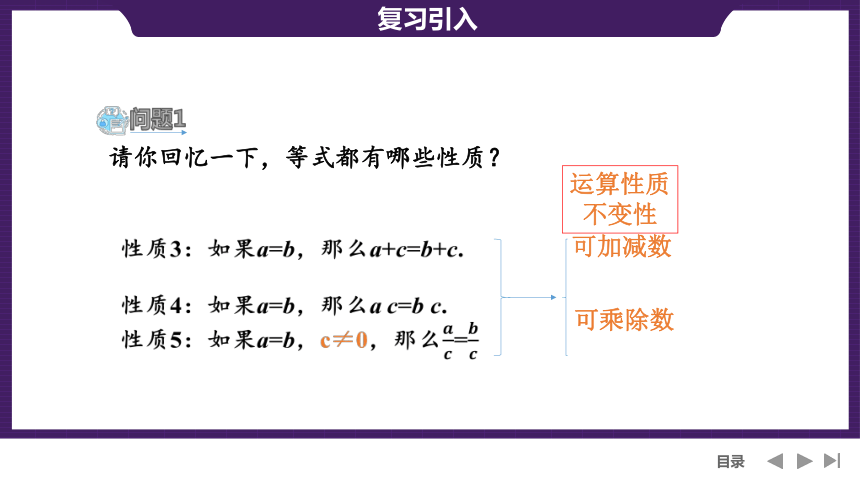
性质3:如果a=b,那么a+c=b+c.
性质4:如果a=b,那么a c=b c.
性质5:如果a=b,c≠0,那么=
运算性质
不变性
可加减数
可乘除数
复习引入
归纳等式基本性质蕴含的本质属性
问题2
“相等关系自身的特点”和
“相等关系对运算保持不变”
性质引入
问题3
请尝试一下!
类比等式的基本性质蕴含的“自身特性”的思想方法,你能猜想并证明不等式的基本性质吗?
性质引入
类比
类比
a=b b=a
a=b,b=c a=c
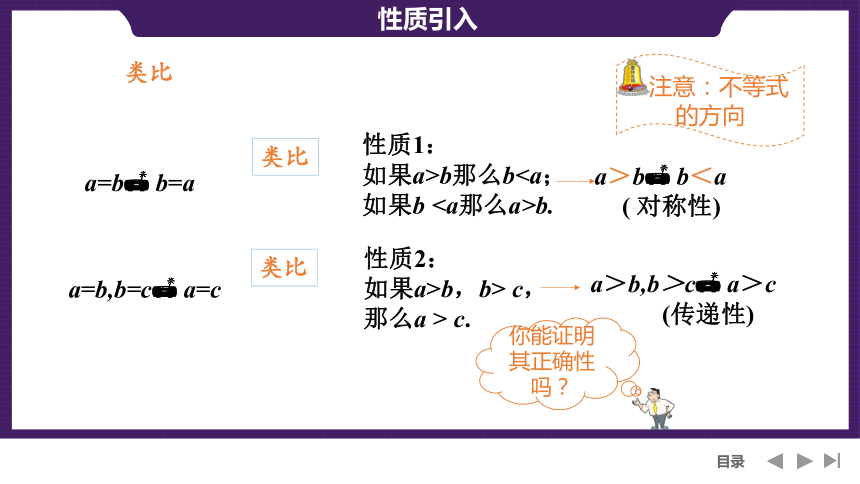
性质1:
如果a>b那么b如果b b.
a>b b<a
( 对称性)
注意:不等式的方向
性质2:
如果a>b,b> c,
那么a > c.
a>b,b>c a>c
(传递性)
类比
你能证明其正确性吗?
性质引入
性质2:如果a>b,b> c,那么a > c.
分析:若要证明a>c,只需要证明a-c>0.
联系a-b>0,b-c>0,a - c=(a - b)+(b - c)>0,
如何证明(a-b)+(b-c)>0?
证明
由两个实数大小关系的基本事实知:
a>b a-b>0
b>c b-c>0
(a-b)+(b-c)>0
a-c>0
a>c
性质引入
问题4
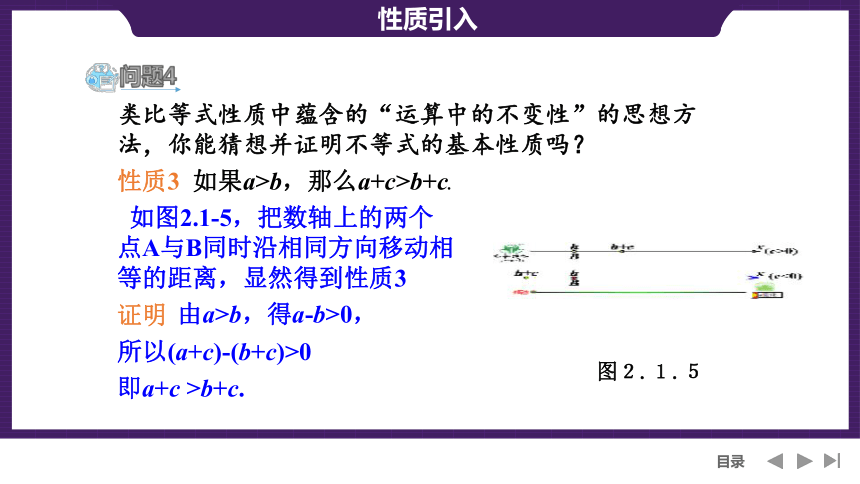
性质3 如果a>b,那么a+c>b+c.
类比等式性质中蕴含的“运算中的不变性”的思想方法,你能猜想并证明不等式的基本性质吗?
图2.1.5
如图2.1-5,把数轴上的两个点A与B同时沿相同方向移动相等的距离,显然得到性质3
证明
由a>b,得a-b>0,
所以(a+c)-(b+c)>0
即a+c >b+c.
性质理解
性质3 如果a>b,那么a+c>b+c.
追问1:用文字语言怎样表达此性质?
不等式的两边都加上同一个实数,所得不等式与原不等式同向.
追问2:你能从性质3中得到什么结论吗?
由性质3可得
a+b>c a+b+(-b)>c+(-b)
a>c-b.
和等式的移项法则相同吗?
性质引入
性质4:
如果a>b,c>0,那么ac >bc;
如果a>b,c<0那么ac < be
分析:要判断ac与bc的大小关系,即要判断ac-bc=(a-b)c与0的大小关系
由于a-b>0,(a-b)c的正负由c的正负决定,从而需要分类讨论.
不等式的两边同乘一个数,为何要分类讨论?
问题5
性质理解
性质4:
如果a>b,c>0,那么ac >bc;
如果a>b,c<0那么ac < bc
不等式两边同乘一个正数,
所得不等式与原不等式同向;
不等式两边同乘一个负数,
所得不等式与原不等式反向.
追问1:用文字语言怎样表述此性质?
注意:不等式两端乘以一个数时,一定要充分考虑这个数的正负,特别是不等式两端同乘以一个式,更应十分注意,有时有必要讨论。
性质引入
性质5:
如果a>b,c>d,那么a+c >b+d.
证法1
分析:若要证明a+c>b+d,只需要证明(a+c)-(b+d)>0.
不等式的两边同加一个不等数,竟然也成立,
请注意这两个数的大小特点,你会证明吗?
问题6
由已知a-b>0,c-d>0,由“正数加正数是正数”这一基本事实,得证.
性质引入
性质5:
如果a>b,c>d,那么a+c >b+d.
证法2
由性质3,得a+c >b+c,b+c >b+d;
由性质2,得a+c>b+d.
温馨提示
两个同向不等式可以相加,且不等式的方向不变。否则不一定不改变方向。
性质引入
有不等式的性质5猜想:
如果a>b,c>d,那么ac >bd;
追问:在不等式的基本性质中,乘法运算不具备“保号性”你认为上述猜想是否正确?如何修正?
性质6:如果a>b>0,c>d>0,那么ac >bd;
提示:
ac>bc
bc>bd
ac>bd
性质引入
追问:如果性质6中a=c,b=d你有何新的结论?
如果a>b>0,那么a2>b2
性质7:如果a>b>0,那么an>bn
(n∈N*, n≥2)
扩展
如果a-b>0则(-a)n>(-b)n
巩固与练习
深化与思考
深化
深化与思考
思考辨析
×
×
√
小结
限时小练
简解答:
课堂作业
1、练习1,2
2、习题2.1第7题
本节内容结束
THANKS
新教材人教版·高中必修第一册
数学
2.1等式性质与不等式性质(2)
第二课时 不等式的性质
第二章 一元二次函数、方程和不等式
要求
课标要求
1.掌握不等式的基本性质.
2.运用不等式的性质解决有关问题.
素养要求
通过学习不等式的性质及运用不等式的性质解决问题,提升数学抽象、逻辑推理及数学运算素养.
复习引入
请你回忆一下,等式都有哪些性质?
问题1
性质1:如果a=b,那么b=a.
性质2:如果a=b,b=c,那么a=C.
自身特性
对称性
传递性
复习引入
请你回忆一下,等式都有哪些性质?
问题1
性质3:如果a=b,那么a+c=b+c.
性质4:如果a=b,那么a c=b c.
性质5:如果a=b,c≠0,那么=
运算性质
不变性
可加减数
可乘除数
复习引入
归纳等式基本性质蕴含的本质属性
问题2
“相等关系自身的特点”和
“相等关系对运算保持不变”
性质引入
问题3
请尝试一下!
类比等式的基本性质蕴含的“自身特性”的思想方法,你能猜想并证明不等式的基本性质吗?
性质引入
类比
类比
a=b b=a
a=b,b=c a=c
性质1:
如果a>b那么b
a>b b<a
( 对称性)
注意:不等式的方向
性质2:
如果a>b,b> c,
那么a > c.
a>b,b>c a>c
(传递性)
类比
你能证明其正确性吗?
性质引入
性质2:如果a>b,b> c,那么a > c.
分析:若要证明a>c,只需要证明a-c>0.
联系a-b>0,b-c>0,a - c=(a - b)+(b - c)>0,
如何证明(a-b)+(b-c)>0?
证明
由两个实数大小关系的基本事实知:
a>b a-b>0
b>c b-c>0
(a-b)+(b-c)>0
a-c>0
a>c
性质引入
问题4
性质3 如果a>b,那么a+c>b+c.
类比等式性质中蕴含的“运算中的不变性”的思想方法,你能猜想并证明不等式的基本性质吗?
图2.1.5
如图2.1-5,把数轴上的两个点A与B同时沿相同方向移动相等的距离,显然得到性质3
证明
由a>b,得a-b>0,
所以(a+c)-(b+c)>0
即a+c >b+c.
性质理解
性质3 如果a>b,那么a+c>b+c.
追问1:用文字语言怎样表达此性质?
不等式的两边都加上同一个实数,所得不等式与原不等式同向.
追问2:你能从性质3中得到什么结论吗?
由性质3可得
a+b>c a+b+(-b)>c+(-b)
a>c-b.
和等式的移项法则相同吗?
性质引入
性质4:
如果a>b,c>0,那么ac >bc;
如果a>b,c<0那么ac < be
分析:要判断ac与bc的大小关系,即要判断ac-bc=(a-b)c与0的大小关系
由于a-b>0,(a-b)c的正负由c的正负决定,从而需要分类讨论.
不等式的两边同乘一个数,为何要分类讨论?
问题5
性质理解
性质4:
如果a>b,c>0,那么ac >bc;
如果a>b,c<0那么ac < bc
不等式两边同乘一个正数,
所得不等式与原不等式同向;
不等式两边同乘一个负数,
所得不等式与原不等式反向.
追问1:用文字语言怎样表述此性质?
注意:不等式两端乘以一个数时,一定要充分考虑这个数的正负,特别是不等式两端同乘以一个式,更应十分注意,有时有必要讨论。
性质引入
性质5:
如果a>b,c>d,那么a+c >b+d.
证法1
分析:若要证明a+c>b+d,只需要证明(a+c)-(b+d)>0.
不等式的两边同加一个不等数,竟然也成立,
请注意这两个数的大小特点,你会证明吗?
问题6
由已知a-b>0,c-d>0,由“正数加正数是正数”这一基本事实,得证.
性质引入
性质5:
如果a>b,c>d,那么a+c >b+d.
证法2
由性质3,得a+c >b+c,b+c >b+d;
由性质2,得a+c>b+d.
温馨提示
两个同向不等式可以相加,且不等式的方向不变。否则不一定不改变方向。
性质引入
有不等式的性质5猜想:
如果a>b,c>d,那么ac >bd;
追问:在不等式的基本性质中,乘法运算不具备“保号性”你认为上述猜想是否正确?如何修正?
性质6:如果a>b>0,c>d>0,那么ac >bd;
提示:
ac>bc
bc>bd
ac>bd
性质引入
追问:如果性质6中a=c,b=d你有何新的结论?
如果a>b>0,那么a2>b2
性质7:如果a>b>0,那么an>bn
(n∈N*, n≥2)
扩展
如果a
巩固与练习
深化与思考
深化
深化与思考
思考辨析
×
×
√
小结
限时小练
简解答:
课堂作业
1、练习1,2
2、习题2.1第7题
本节内容结束
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
