第四章 基本平面图形培优专练 2022-2023学年北师大版数学七年级上册(含答案)
文档属性
| 名称 | 第四章 基本平面图形培优专练 2022-2023学年北师大版数学七年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 00:00:00 | ||
图片预览


文档简介
《第四章 基本平面图形》培优专练
一、选择题
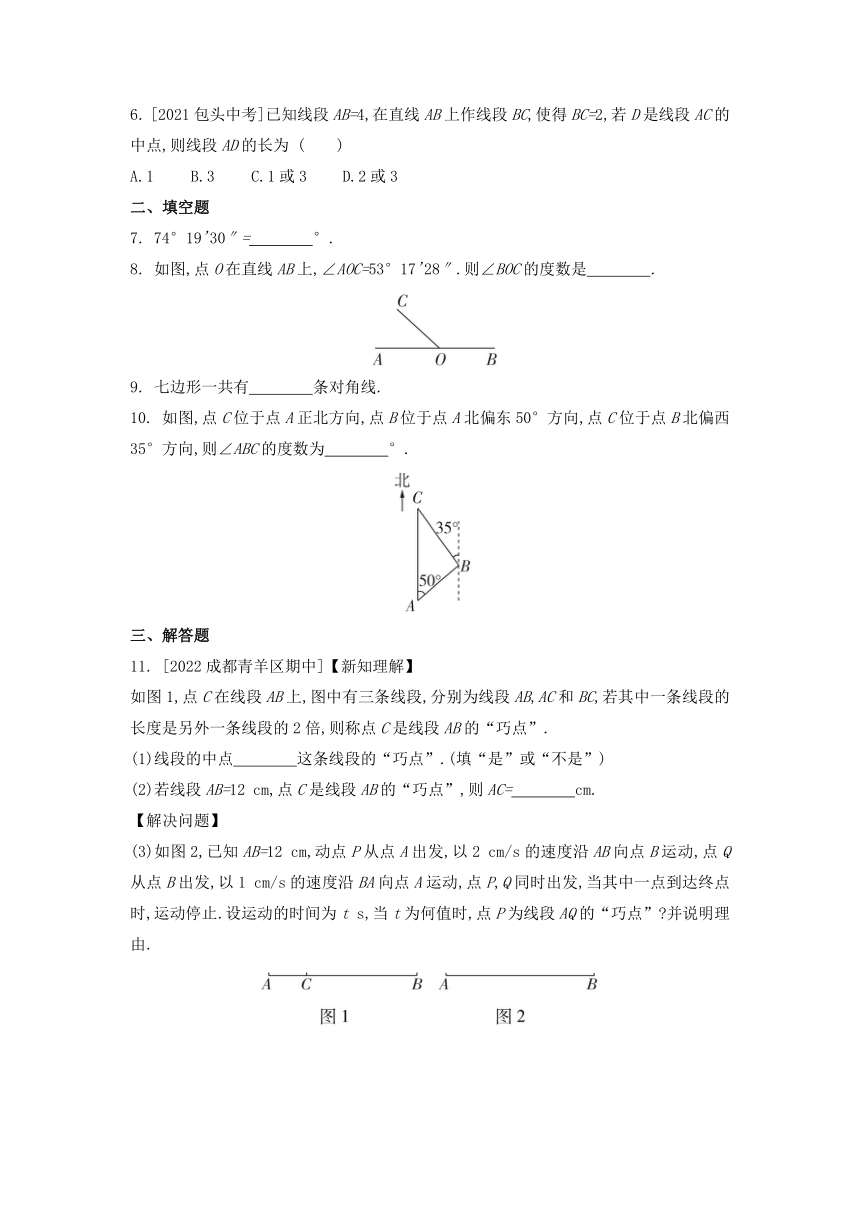
1. 如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是 ( )
A.a B.b C.c D.d
2. 已知扇形的半径为6,圆心角为150°,则它的面积是 ( )
A.π B.3π C.5π D.15π
3. 点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12 cm,则线段BD的长为 ( )
A.10 cm B.8 cm
C.10 cm或8 cm D.2 cm或4 cm
4. 如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD= ( )
A.30° B.40° C.50° D.60°
5. [2021青海中考]如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是 ( )
A.π m2 B.π m2
C.π m2 D.π m2
6. [2021包头中考]已知线段AB=4,在直线AB上作线段BC,使得BC=2,若D是线段AC的中点,则线段AD的长为 ( )
A.1 B.3 C.1或3 D.2或3
二、填空题
7. 74°19'30″= °.
8. 如图,点O在直线AB上,∠AOC=53°17'28″.则∠BOC的度数是 .
9. 七边形一共有 条对角线.
10. 如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
三、解答题
11. [2022成都青羊区期中]【新知理解】
如图1,点C在线段AB上,图中有三条线段,分别为线段AB,AC和BC,若其中一条线段的长度是另外一条线段的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”.(填“是”或“不是”)
(2)若线段AB=12 cm,点C是线段AB的“巧点”,则AC= cm.
【解决问题】
(3)如图2,已知AB=12 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B运动,点Q从点B出发,以1 cm/s的速度沿BA向点A运动,点P,Q同时出发,当其中一点到达终点时,运动停止.设运动的时间为t s,当t为何值时,点P为线段AQ的“巧点” 并说明理由.
12. [探究角之间的数量关系]如图,O为直线AB上一点,∠BOC=α.
(1)如图1,若α=40°,OD平分∠AOC,∠DOE=90°,求∠AOE的度数;
(2)如图2,若∠AOD=∠AOC,∠DOE=60°,请用α表示∠AOE的度数;
(3)如图3,若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),请用α和n表示∠AOE的度数.(直接写出结果)
13. 如图,已知OC,OD是∠AOB内部的两条射线,OC在∠AOD内部,且OE平分∠AOC,OF平分∠DOB.
(1)若∠AOB=160°,∠COD=40°,则∠EOF的度数为 .
(2)若∠AOB=α,∠COD=β,求∠EOF的度数.
(3)观察(1)(2)的结果,可得∠EOF,∠AOB,∠COD之间的数量关系为 .
14. [2022重庆北碚区期末]如图,已知数轴上有三点A,B,C,它们表示的数分别为a,b,c,且c-b=b-a,点C表示的数是20.
(1)若BC=30,求a,b的值;
(2)在(1)的条件下,动点P,Q分别从A,C两点同时出发向左运动,同时动点R从点B出发向右运动,点P,R,Q的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段PR的中点,点N为线段RQ的中点,在点R,Q相遇前,点P,Q,R运动多少秒时恰好满足 MR=4RN
参考答案
一、选择题
1.A 利用直尺画出图形,如图所示,可以看出线段a与m在同一直线上.
2.D 扇形的面积为π×62=15π.
3.C 因为C是线段AB的中点,AB=12 cm,所以AC=BC=AB=×12=6(cm).①如图,当AD=AC时,BD=BC+CD=BC+AC=6+4=10(cm);②如图,当AD'=AC时,BD'=BC+CD'=BC+AC=6+2=8(cm).综上,线段BD的长为10 cm或8 cm.
4.C 易知∠AOB=∠COD=90°,因为∠AOC=130°,所以∠BOC=∠AOC-∠AOB=40°,所以∠BOD=∠COD-∠BOC=50°.
5.B 如图,扇形DOE的圆心角是90°,半径是5 m,所以其面积为π×52=π(m2),扇形BCD的圆心角是180°-120°=60°,半径是5-4=1(m),所以其面积为π×12=(m2),所以小羊A在草地上的最大活动区域面积为π+=π(m2).
6.C 根据题意,分两种情况:①如图1,当点C在线段AB上时,因为AB=4,BC=2,所以AC=AB-BC=2,因为D是线段AC的中点,所以AD=AC=×2=1;②如图2,当点C在线段AB的延长线上时,因为AB=4,BC=2,所以AC=AB+BC=6,因为D是线段AC的中点,所以AD=AC=×6=3.所以线段AD的长为1或3.
二、填空题
7.74.325 30×()'=0.5',19'+0.5'=19.5',19.5×()°=0.325°,74°+0.325°=74.325°.
8.126°42'32″ 因为点O在直线AB上,且∠AOC=53°17'28″,所以∠BOC=180°-∠AOC=180°-53°17'28″=126°42'32″.
9.14 七边形的对角线总共有=14条.
10.95 如图,由题意可得,点B位于点A北偏东50°方向,则点A位于点B南偏西50°方向,即∠1=50°,则∠ABC=180°-35°-50°=95°.
三、解答题
1.解:(1)是
(2)4,6或8
①当AB=2AC时,AC=6 cm;②当AC=2BC时,因为AC+BC=AB=12 cm,所以AC=8 cm;③当BC=2AC时,因为AC+BC=AB=
12 cm,所以AC=4 cm.综上,AC=4 cm,6 cm或8 cm.
(3)当t为,3或时,点P为线段AQ的“巧点”.理由如下:
由题意知,AP=2t cm,BQ=t cm,
所以AQ=(12-t)cm,
因为点P为AQ的“巧点”,所以点P在线段AQ上,
①当AQ=2AP时,12-t=4t,所以t=;
②当AP=2PQ时,AP=AQ,即2t=(12-t),所以t=3;
③当PQ=2AP时,AP=AQ,即2t=(12-t),所以t=.
所以当t为,3或时,点P为线段AQ的“巧点”.
2.解:(1)因为∠BOC=40°,
所以∠AOC=180°-∠BOC=140°,
又因为OD平分∠AOC,
所以∠AOD=∠DOC=∠AOC=70°.
因为∠DOE=90°,所以∠AOE=90°-70°=20°.
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180°-3x=α,
所以x=,
所以∠AOE=60°-x=60°-=α.
(3)∠AOE=.
设∠AOD=y,则∠DOC=(n-1)y,∠BOC=180°-ny=α,
所以y=,
所以∠AOE=-=.
7.解:(1)100°
因为OE平分∠AOC,OF平分∠BOD,
所以∠EOC=∠AOC,∠DOF=∠BOD,
所以∠EOF=∠EOC+∠COD+∠DOF=∠AOC+∠COD+∠COD+∠BOD=(∠AOC+∠COD+∠BOD)+
∠COD=∠AOB+∠COD=(∠AOB+∠COD)=(160°+40°)=100°.
(2)因为OE平分∠AOC,OF平分∠BOD,
所以∠EOC=∠AOC,∠DOF=∠BOD,
所以∠EOF=∠EOC+∠COD+∠DOF=∠AOC+∠COD+∠COD+∠BOD=(∠AOC+∠COD+∠BOD)+
∠COD=∠AOB+∠COD=(∠AOB+∠COD)=(α+β).
(3)∠EOF=(∠AOB+∠COD)
8.解:(1)因为BC=30,所以c-b=b-a=30,
因为点C表示的数是20,
所以点A表示的数为20-60=-40,点B表示的数为20-30=-10,
所以a的值为-40,b的值为-10.
(2)如图,由(1)可得AB=BC=30,
设在点R,Q相遇前,点P,Q,R运动x秒时恰好满足MR=4RN,则AP=8x,BR=4x,CQ=2x.
因为点M,N分别是线段PR,RQ的中点,
所以MR=(8x+4x+30),RN=(30-4x-2x),
所以当MR=4RN时,(8x+4x+30)=4×(30-4x-2x),
所以x=2.5,
所以在点R,Q相遇前,点P,Q,R运动2.5秒时恰好满足MR=4RN.
一、选择题
1. 如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是 ( )
A.a B.b C.c D.d
2. 已知扇形的半径为6,圆心角为150°,则它的面积是 ( )
A.π B.3π C.5π D.15π
3. 点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12 cm,则线段BD的长为 ( )
A.10 cm B.8 cm
C.10 cm或8 cm D.2 cm或4 cm
4. 如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD= ( )
A.30° B.40° C.50° D.60°
5. [2021青海中考]如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是 ( )
A.π m2 B.π m2
C.π m2 D.π m2
6. [2021包头中考]已知线段AB=4,在直线AB上作线段BC,使得BC=2,若D是线段AC的中点,则线段AD的长为 ( )
A.1 B.3 C.1或3 D.2或3
二、填空题
7. 74°19'30″= °.
8. 如图,点O在直线AB上,∠AOC=53°17'28″.则∠BOC的度数是 .
9. 七边形一共有 条对角线.
10. 如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
三、解答题
11. [2022成都青羊区期中]【新知理解】
如图1,点C在线段AB上,图中有三条线段,分别为线段AB,AC和BC,若其中一条线段的长度是另外一条线段的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”.(填“是”或“不是”)
(2)若线段AB=12 cm,点C是线段AB的“巧点”,则AC= cm.
【解决问题】
(3)如图2,已知AB=12 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B运动,点Q从点B出发,以1 cm/s的速度沿BA向点A运动,点P,Q同时出发,当其中一点到达终点时,运动停止.设运动的时间为t s,当t为何值时,点P为线段AQ的“巧点” 并说明理由.
12. [探究角之间的数量关系]如图,O为直线AB上一点,∠BOC=α.
(1)如图1,若α=40°,OD平分∠AOC,∠DOE=90°,求∠AOE的度数;
(2)如图2,若∠AOD=∠AOC,∠DOE=60°,请用α表示∠AOE的度数;
(3)如图3,若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),请用α和n表示∠AOE的度数.(直接写出结果)
13. 如图,已知OC,OD是∠AOB内部的两条射线,OC在∠AOD内部,且OE平分∠AOC,OF平分∠DOB.
(1)若∠AOB=160°,∠COD=40°,则∠EOF的度数为 .
(2)若∠AOB=α,∠COD=β,求∠EOF的度数.
(3)观察(1)(2)的结果,可得∠EOF,∠AOB,∠COD之间的数量关系为 .
14. [2022重庆北碚区期末]如图,已知数轴上有三点A,B,C,它们表示的数分别为a,b,c,且c-b=b-a,点C表示的数是20.
(1)若BC=30,求a,b的值;
(2)在(1)的条件下,动点P,Q分别从A,C两点同时出发向左运动,同时动点R从点B出发向右运动,点P,R,Q的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段PR的中点,点N为线段RQ的中点,在点R,Q相遇前,点P,Q,R运动多少秒时恰好满足 MR=4RN
参考答案
一、选择题
1.A 利用直尺画出图形,如图所示,可以看出线段a与m在同一直线上.
2.D 扇形的面积为π×62=15π.
3.C 因为C是线段AB的中点,AB=12 cm,所以AC=BC=AB=×12=6(cm).①如图,当AD=AC时,BD=BC+CD=BC+AC=6+4=10(cm);②如图,当AD'=AC时,BD'=BC+CD'=BC+AC=6+2=8(cm).综上,线段BD的长为10 cm或8 cm.
4.C 易知∠AOB=∠COD=90°,因为∠AOC=130°,所以∠BOC=∠AOC-∠AOB=40°,所以∠BOD=∠COD-∠BOC=50°.
5.B 如图,扇形DOE的圆心角是90°,半径是5 m,所以其面积为π×52=π(m2),扇形BCD的圆心角是180°-120°=60°,半径是5-4=1(m),所以其面积为π×12=(m2),所以小羊A在草地上的最大活动区域面积为π+=π(m2).
6.C 根据题意,分两种情况:①如图1,当点C在线段AB上时,因为AB=4,BC=2,所以AC=AB-BC=2,因为D是线段AC的中点,所以AD=AC=×2=1;②如图2,当点C在线段AB的延长线上时,因为AB=4,BC=2,所以AC=AB+BC=6,因为D是线段AC的中点,所以AD=AC=×6=3.所以线段AD的长为1或3.
二、填空题
7.74.325 30×()'=0.5',19'+0.5'=19.5',19.5×()°=0.325°,74°+0.325°=74.325°.
8.126°42'32″ 因为点O在直线AB上,且∠AOC=53°17'28″,所以∠BOC=180°-∠AOC=180°-53°17'28″=126°42'32″.
9.14 七边形的对角线总共有=14条.
10.95 如图,由题意可得,点B位于点A北偏东50°方向,则点A位于点B南偏西50°方向,即∠1=50°,则∠ABC=180°-35°-50°=95°.
三、解答题
1.解:(1)是
(2)4,6或8
①当AB=2AC时,AC=6 cm;②当AC=2BC时,因为AC+BC=AB=12 cm,所以AC=8 cm;③当BC=2AC时,因为AC+BC=AB=
12 cm,所以AC=4 cm.综上,AC=4 cm,6 cm或8 cm.
(3)当t为,3或时,点P为线段AQ的“巧点”.理由如下:
由题意知,AP=2t cm,BQ=t cm,
所以AQ=(12-t)cm,
因为点P为AQ的“巧点”,所以点P在线段AQ上,
①当AQ=2AP时,12-t=4t,所以t=;
②当AP=2PQ时,AP=AQ,即2t=(12-t),所以t=3;
③当PQ=2AP时,AP=AQ,即2t=(12-t),所以t=.
所以当t为,3或时,点P为线段AQ的“巧点”.
2.解:(1)因为∠BOC=40°,
所以∠AOC=180°-∠BOC=140°,
又因为OD平分∠AOC,
所以∠AOD=∠DOC=∠AOC=70°.
因为∠DOE=90°,所以∠AOE=90°-70°=20°.
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180°-3x=α,
所以x=,
所以∠AOE=60°-x=60°-=α.
(3)∠AOE=.
设∠AOD=y,则∠DOC=(n-1)y,∠BOC=180°-ny=α,
所以y=,
所以∠AOE=-=.
7.解:(1)100°
因为OE平分∠AOC,OF平分∠BOD,
所以∠EOC=∠AOC,∠DOF=∠BOD,
所以∠EOF=∠EOC+∠COD+∠DOF=∠AOC+∠COD+∠COD+∠BOD=(∠AOC+∠COD+∠BOD)+
∠COD=∠AOB+∠COD=(∠AOB+∠COD)=(160°+40°)=100°.
(2)因为OE平分∠AOC,OF平分∠BOD,
所以∠EOC=∠AOC,∠DOF=∠BOD,
所以∠EOF=∠EOC+∠COD+∠DOF=∠AOC+∠COD+∠COD+∠BOD=(∠AOC+∠COD+∠BOD)+
∠COD=∠AOB+∠COD=(∠AOB+∠COD)=(α+β).
(3)∠EOF=(∠AOB+∠COD)
8.解:(1)因为BC=30,所以c-b=b-a=30,
因为点C表示的数是20,
所以点A表示的数为20-60=-40,点B表示的数为20-30=-10,
所以a的值为-40,b的值为-10.
(2)如图,由(1)可得AB=BC=30,
设在点R,Q相遇前,点P,Q,R运动x秒时恰好满足MR=4RN,则AP=8x,BR=4x,CQ=2x.
因为点M,N分别是线段PR,RQ的中点,
所以MR=(8x+4x+30),RN=(30-4x-2x),
所以当MR=4RN时,(8x+4x+30)=4×(30-4x-2x),
所以x=2.5,
所以在点R,Q相遇前,点P,Q,R运动2.5秒时恰好满足MR=4RN.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
