2022-2023学年人教版数学七年级下册8.3 实际问题与二元一次方程组 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册8.3 实际问题与二元一次方程组 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 08:43:31 | ||
图片预览


文档简介
8.3 实际问题与二元一次方程组 同步练习
一、单选题
1.《九章算术》中有这样一个题:今有二马、一牛价过-一万、如半马之价.一马、二牛价不满一万、如半牛之价.问牛、马价各几何?其意思是:今有2匹马、1头牛的总价超过1万钱,其超出的钱数相当于匹马的价格,1匹马、2头牛的总价不足1万钱,所差的钱数相当于头牛的价格.问每头牛、每匹马的价格各是多少?设每匹马的价格为x万钱,每头牛的价格为y万钱,则可建立方程组为( )
A. B.
C. D.
2.已知甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数.若设甲数为x,乙数为y,由题意得方程组( )
A. B. C. D.
3.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术,其中方程术是《九章算术》最高的数学成就.《九章算术》 中记载:“今有共买鸡,人出八,盈三;人出七,不足四. 问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱. 问人数和鸡的价钱各是多少?”设人数有人,鸡的价钱是钱,则可列方程组为( )
A. B. C. D.
4.母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
5.现有57张铁皮盒子,每张铁皮做8个盒身或22个盒底,一个盒身与两个盒底配成一个盒子设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A. B.
C. D.
6.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳五尺四寸:屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为( )
A. B. C. D.
7.某班45名同学去看演出,甲种票每张24元,乙种票每张18元,购票款为960元.设甲种票买了x张,乙种票买了y张,则依题意可列出方程组( )
A. B. C. D.
8.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能使生产的螺栓和螺帽刚好配套?若设生产螺栓x人,生产螺帽y人,则列方程组得( )
A. B. C. D.
9.如果方程组的解是二元一次方程的一个解,那么的值为( )
A.1 B.6 C.3 D.2
10.若方程组的解与是互为相反数,则的值为( )
A.4 B.6 C.-6 D.-1
二、填空题
11.请写出一个二元一次方程组,使该方程组无解.你写的方程组是______.
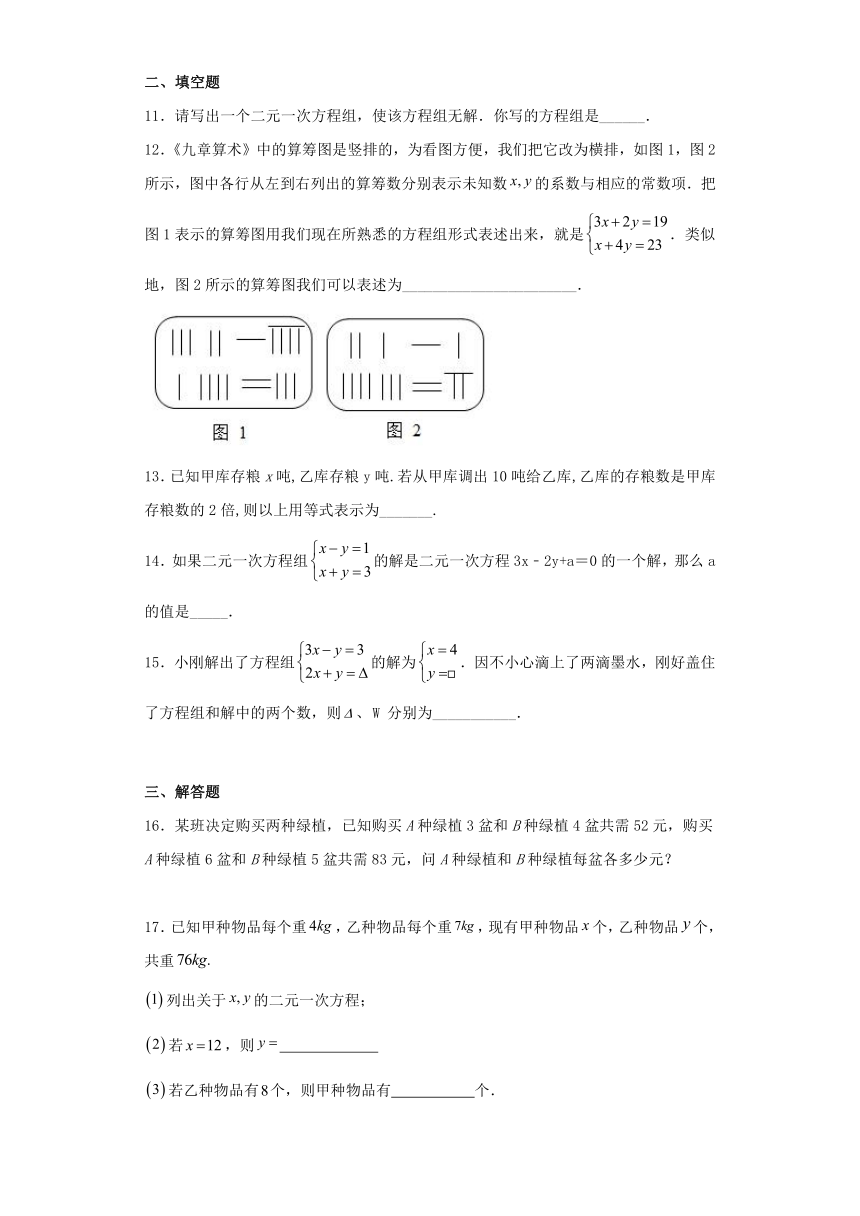
12.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项.把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来,就是.类似地,图2所示的算筹图我们可以表述为_______________________.
13.已知甲库存粮x吨,乙库存粮y吨.若从甲库调出10吨给乙库,乙库的存粮数是甲库存粮数的2倍,则以上用等式表示为_______.
14.如果二元一次方程组的解是二元一次方程3x﹣2y+a=0的一个解,那么a的值是_____.
15.小刚解出了方程组的解为.因不小心滴上了两滴墨水,刚好盖住了方程组和解中的两个数,则、分别为___________.
三、解答题
16.某班决定购买两种绿植,已知购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元,问A种绿植和B种绿植每盆各多少元?
17.已知甲种物品每个重,乙种物品每个重,现有甲种物品个,乙种物品个,共重
列出关于的二元一次方程;
若,则
若乙种物品有个,则甲种物品有 个.
18.如果关于的二元一次方程组的解是,那么关于的二元一次方程组的解是什么?
19.在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆.”
乙同学说:“四环路比三环路车流量每小时多2000辆.”
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍.”
请你根据他们提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
20.某中学为丰富学生的校园生活,准备从商店购实若干个足球和篮球,已知购买2个足球和个篮球共需420元,购买3个足球比1个篮球要多花70元
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球30个,则学校有哪几种购买方案?
(3)在“五 一”期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
一次性购买的总金额 优惠措施
不超过300元 不优惠
超过300元且不超过500元 售价打九折
超过500元 售价打八折
按上述优惠条件,七年级(1)班第一天只购买足球一次性付款200元,第二天只购买篮球打折后一次性付款360元,求该班购买足球、篮球各多少个?而(2)班一次性购买这两种球,同样也是花560元,求该班购买足球、篮球各多少个?
参考答案
1.D
2.D
3.A
4.B
5.A
6.C
7.A
8.C
9.D
10.C
11.(答案不唯一)
12.
13.
14.﹣4
15.17,9
16.A种绿植每盆8元,B种绿植每盆7元.
【详解】解:设A种绿植和B种绿植每盆x元和y元,依题意,得
,
解方程得:
,
答:A种绿植每盆8元,B种绿植每盆7元.
17.(1);(2);(3)
【详解】(1)由题意知;
(2)当x=12时,48+7y=76,
解得y=4,
故答案为:4;
(3)当y=8时,4x+56=76,
解得:x=5,即甲种物品有5个,
故答案为:5.
18.
【详解】解:∵关于x,y的二元一次方程组的解是,
,解得
∴可化为
解得,故答案为.
19.高峰时段三环路车流量为每小时11000辆,四环路车流量为每小时13000辆.
【详解】解:设高峰时段三环路车流量为每小时x辆,四环路车流量为每小时y辆.根据题意得:
解得:.
答:高峰时段三环路车流量为每小时11000辆,四环路车流量为每小时13000辆.
20.(1)足球50元,篮球80元;(2)4种,具体方案见解析;(3)购买足球4个,购买篮球5个;足球6个,篮球5个
【详解】(1)设一个足球x元,一个篮球y元,
由题意可得:,
解得:,
答:一个足球50元,一个篮球80元;
(2)设购买足球m个,则购买篮球个,
由题意可得:,
解得:,
∵,
∴,
则m的取值为:27,28,29,30;
故有四种方案:
①购买足球27个,购买篮球3个;
②购买足球28个,购买篮球2个;
③购买足球29个,购买篮球1个;
④购买足球30个,购买篮球0个;
(3)第一次购买足球:(个),第一次购买篮球:,
设第二次购买足球a个,购买篮球b个,
则,
,
∵a、b均为整数,
∴当时,a为整数6,
故第一次购买足球4个,购买篮球5个;第二次购买足球6个,购买篮球5个;
一、单选题
1.《九章算术》中有这样一个题:今有二马、一牛价过-一万、如半马之价.一马、二牛价不满一万、如半牛之价.问牛、马价各几何?其意思是:今有2匹马、1头牛的总价超过1万钱,其超出的钱数相当于匹马的价格,1匹马、2头牛的总价不足1万钱,所差的钱数相当于头牛的价格.问每头牛、每匹马的价格各是多少?设每匹马的价格为x万钱,每头牛的价格为y万钱,则可建立方程组为( )
A. B.
C. D.
2.已知甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数.若设甲数为x,乙数为y,由题意得方程组( )
A. B. C. D.
3.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术,其中方程术是《九章算术》最高的数学成就.《九章算术》 中记载:“今有共买鸡,人出八,盈三;人出七,不足四. 问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱. 问人数和鸡的价钱各是多少?”设人数有人,鸡的价钱是钱,则可列方程组为( )
A. B. C. D.
4.母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
5.现有57张铁皮盒子,每张铁皮做8个盒身或22个盒底,一个盒身与两个盒底配成一个盒子设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A. B.
C. D.
6.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳五尺四寸:屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为( )
A. B. C. D.
7.某班45名同学去看演出,甲种票每张24元,乙种票每张18元,购票款为960元.设甲种票买了x张,乙种票买了y张,则依题意可列出方程组( )
A. B. C. D.
8.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能使生产的螺栓和螺帽刚好配套?若设生产螺栓x人,生产螺帽y人,则列方程组得( )
A. B. C. D.
9.如果方程组的解是二元一次方程的一个解,那么的值为( )
A.1 B.6 C.3 D.2
10.若方程组的解与是互为相反数,则的值为( )
A.4 B.6 C.-6 D.-1
二、填空题
11.请写出一个二元一次方程组,使该方程组无解.你写的方程组是______.
12.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项.把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来,就是.类似地,图2所示的算筹图我们可以表述为_______________________.
13.已知甲库存粮x吨,乙库存粮y吨.若从甲库调出10吨给乙库,乙库的存粮数是甲库存粮数的2倍,则以上用等式表示为_______.
14.如果二元一次方程组的解是二元一次方程3x﹣2y+a=0的一个解,那么a的值是_____.
15.小刚解出了方程组的解为.因不小心滴上了两滴墨水,刚好盖住了方程组和解中的两个数,则、分别为___________.
三、解答题
16.某班决定购买两种绿植,已知购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元,问A种绿植和B种绿植每盆各多少元?
17.已知甲种物品每个重,乙种物品每个重,现有甲种物品个,乙种物品个,共重
列出关于的二元一次方程;
若,则
若乙种物品有个,则甲种物品有 个.
18.如果关于的二元一次方程组的解是,那么关于的二元一次方程组的解是什么?
19.在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆.”
乙同学说:“四环路比三环路车流量每小时多2000辆.”
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍.”
请你根据他们提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
20.某中学为丰富学生的校园生活,准备从商店购实若干个足球和篮球,已知购买2个足球和个篮球共需420元,购买3个足球比1个篮球要多花70元
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球30个,则学校有哪几种购买方案?
(3)在“五 一”期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
一次性购买的总金额 优惠措施
不超过300元 不优惠
超过300元且不超过500元 售价打九折
超过500元 售价打八折
按上述优惠条件,七年级(1)班第一天只购买足球一次性付款200元,第二天只购买篮球打折后一次性付款360元,求该班购买足球、篮球各多少个?而(2)班一次性购买这两种球,同样也是花560元,求该班购买足球、篮球各多少个?
参考答案
1.D
2.D
3.A
4.B
5.A
6.C
7.A
8.C
9.D
10.C
11.(答案不唯一)
12.
13.
14.﹣4
15.17,9
16.A种绿植每盆8元,B种绿植每盆7元.
【详解】解:设A种绿植和B种绿植每盆x元和y元,依题意,得
,
解方程得:
,
答:A种绿植每盆8元,B种绿植每盆7元.
17.(1);(2);(3)
【详解】(1)由题意知;
(2)当x=12时,48+7y=76,
解得y=4,
故答案为:4;
(3)当y=8时,4x+56=76,
解得:x=5,即甲种物品有5个,
故答案为:5.
18.
【详解】解:∵关于x,y的二元一次方程组的解是,
,解得
∴可化为
解得,故答案为.
19.高峰时段三环路车流量为每小时11000辆,四环路车流量为每小时13000辆.
【详解】解:设高峰时段三环路车流量为每小时x辆,四环路车流量为每小时y辆.根据题意得:
解得:.
答:高峰时段三环路车流量为每小时11000辆,四环路车流量为每小时13000辆.
20.(1)足球50元,篮球80元;(2)4种,具体方案见解析;(3)购买足球4个,购买篮球5个;足球6个,篮球5个
【详解】(1)设一个足球x元,一个篮球y元,
由题意可得:,
解得:,
答:一个足球50元,一个篮球80元;
(2)设购买足球m个,则购买篮球个,
由题意可得:,
解得:,
∵,
∴,
则m的取值为:27,28,29,30;
故有四种方案:
①购买足球27个,购买篮球3个;
②购买足球28个,购买篮球2个;
③购买足球29个,购买篮球1个;
④购买足球30个,购买篮球0个;
(3)第一次购买足球:(个),第一次购买篮球:,
设第二次购买足球a个,购买篮球b个,
则,
,
∵a、b均为整数,
∴当时,a为整数6,
故第一次购买足球4个,购买篮球5个;第二次购买足球6个,购买篮球5个;
