7.1.2 全概率公式 课件(共20张PPT)
文档属性
| 名称 | 7.1.2 全概率公式 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 735.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 06:44:18 | ||
图片预览








文档简介
(共20张PPT)
第七章 随机变量及其分布
人教A版2019必修第三册
7.1.2 全概率公式
1.条件概率
3.概率的乘法公式
复习导入:
通过上一节的学习,我们知道,在求一个复杂事件的概率时,可以先将其表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率. 下面,我们再看一个求复杂事件概率的问题.
思考:从有 a 个红球和 b 个篮球的袋子中,每次随机摸出1个球,摸出的球不再放回. 显然,第1次摸到红球的概率为 . 那么第2次摸到红球的概率是多大?如何计算这个概率呢?
分析:因为抽签具有公平性,所以第2次摸到红球的概率也应该是 .但是这个结果并不显然,因为第2次摸球的结果受第1次摸球结果的影响. 下面我们给出严格的推导过程.
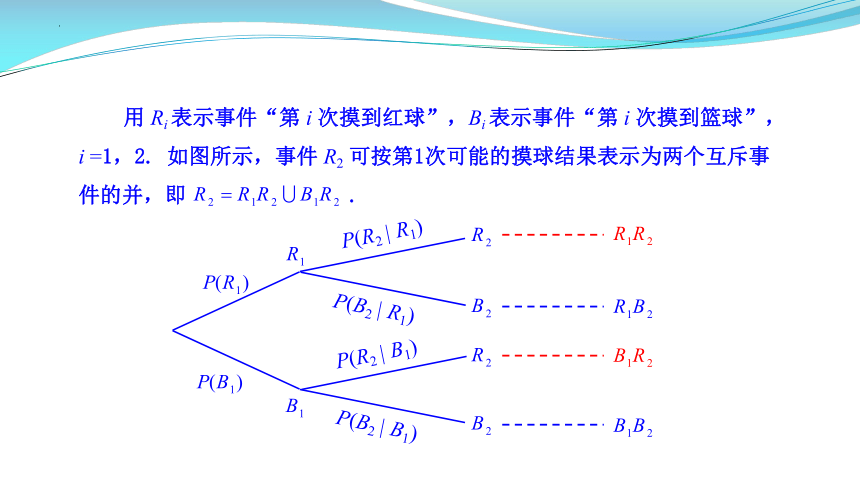
用 Ri 表示事件“第 i 次摸到红球”,Bi 表示事件“第 i 次摸到篮球”,i =1,2. 如图所示,事件 R2 可按第1次可能的摸球结果表示为两个互斥事件的并,即 .
P(R2 | R1)
P(B2 | R1)
P(R2 | B1)
P(B2 | B1)
利用概率的加法公式和乘法公式,得
上述过程采用的方法是:按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
一般地,设A1,A2,···,An是一组两两互斥的事件,
,且 , ,则对任意的事件 ,有
全概率公式
我们称上面的公式为全概率公式. 全概率公式是概率论中最基本的公式之一.
对全概率公式的理解
使用全概率公式计算目标事件 B 的概率,必须是找到样本空间 Ω 的一个事件组 A1,A2,…,An,它们满足:①两两互斥;② ,而这一事件组恰恰可以理解为是事件 B 产生的几个原因.全概率公式相当于将产生 B 的全部原因一一进行考察,将每一个可能性都考虑进来,这就是“全”的含义所在.
直观解释为如图,B 发生的概率与P(B│Ai)(i=1,2, ,n)有关,且 B 发生的概率等于所有这些概率的和,即
例4 某学校有 A,B 两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐. 如果第1天去 A 餐厅,那么第2天去 A 餐厅的概率为0.6;如果第1天去 B 餐厅,那么第2天去 A 餐厅的概率为0.8. 计算王同学第2天去 A 餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
两个事件的全概率公式
全概率问题求解策略
(1)拆分:将样本空间拆分成对立的两部分,如A1,A2(或 A 与 );
(2)计算:利用乘法公式计算每一部分的概率;
(3)求和:所求事件的概率就是各种可能情形 Ai 发生的可能性与已知在 Ai发生的条件下事件 B 发生的可能性的乘积之和,即
.
例5 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知第1,2,3台车床加工的零件分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
设B=“任取一个零件为次品”, Ai=“零件为第i台车床加工” (i=1, 2, 3), 则
解:
多个事件的全概率公式
例5 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知第1,2,3台车床加工的零件分别占总数的25%,30%,45%.
(2)如果取到的零件是次品,计算它是第1台车床加工的概率
如果取到的零件是次品,计算它是第i(i=1, 2, 3)台车床加工的概率,就是计算在B发生的条件下,事件Ai发生的概率,即
解:
“化整为零”求全概率问题
(1)已知事件 B 的发生有各种可能的情形Ai(i =1,2,3),事件 B 发生的可能性,就是各种可能情形 Ai 发生的可能性与已知在 Ai 发生的条件下事件 B 发生的可能性的乘积之和,即 .
(2)在上例中,P(Ai)是试验之前就已知的概率,它是第 i 台车床加工的零件所占的比例,称为先验概率. 当已知抽到的零件是次品( B 发生),
是这件次品来自第 i 台车床加工的可能性大小,通常称为后验概
率. 如果对加工的次品,要求操作员承担相应的责任,那么 , , 就分别是第1,2,3台车床操作员应承担的份额.
将上例中的问题一般化,就可以得到贝叶斯公式.
贝叶斯公式:设A1,A2,...,An是一组两两互斥的事件,
,且 ,则对任意的事件 ,
,有
注意:选讲内容,不作考试要求。
例6 在数字通信中,信号是由数字0和1组成的序列. 由于随机因素的
干扰,发送的信号0或1有可能被错误地接收为1或0. 已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
解:
解:
1. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题
完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
设A=“选到有思路的题”, B=“选到的题做对”, 则由全概率公式, 可得
解:
2. 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
设A=“取到合格品”, Bi=“取到的产品来自第i批”(i=1, 2), 则
课堂小结:
1. 全概率公式:
2. 贝叶斯公式:
第七章 随机变量及其分布
人教A版2019必修第三册
7.1.2 全概率公式
1.条件概率
3.概率的乘法公式
复习导入:
通过上一节的学习,我们知道,在求一个复杂事件的概率时,可以先将其表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率. 下面,我们再看一个求复杂事件概率的问题.
思考:从有 a 个红球和 b 个篮球的袋子中,每次随机摸出1个球,摸出的球不再放回. 显然,第1次摸到红球的概率为 . 那么第2次摸到红球的概率是多大?如何计算这个概率呢?
分析:因为抽签具有公平性,所以第2次摸到红球的概率也应该是 .但是这个结果并不显然,因为第2次摸球的结果受第1次摸球结果的影响. 下面我们给出严格的推导过程.
用 Ri 表示事件“第 i 次摸到红球”,Bi 表示事件“第 i 次摸到篮球”,i =1,2. 如图所示,事件 R2 可按第1次可能的摸球结果表示为两个互斥事件的并,即 .
P(R2 | R1)
P(B2 | R1)
P(R2 | B1)
P(B2 | B1)
利用概率的加法公式和乘法公式,得
上述过程采用的方法是:按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
一般地,设A1,A2,···,An是一组两两互斥的事件,
,且 , ,则对任意的事件 ,有
全概率公式
我们称上面的公式为全概率公式. 全概率公式是概率论中最基本的公式之一.
对全概率公式的理解
使用全概率公式计算目标事件 B 的概率,必须是找到样本空间 Ω 的一个事件组 A1,A2,…,An,它们满足:①两两互斥;② ,而这一事件组恰恰可以理解为是事件 B 产生的几个原因.全概率公式相当于将产生 B 的全部原因一一进行考察,将每一个可能性都考虑进来,这就是“全”的含义所在.
直观解释为如图,B 发生的概率与P(B│Ai)(i=1,2, ,n)有关,且 B 发生的概率等于所有这些概率的和,即
例4 某学校有 A,B 两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐. 如果第1天去 A 餐厅,那么第2天去 A 餐厅的概率为0.6;如果第1天去 B 餐厅,那么第2天去 A 餐厅的概率为0.8. 计算王同学第2天去 A 餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
两个事件的全概率公式
全概率问题求解策略
(1)拆分:将样本空间拆分成对立的两部分,如A1,A2(或 A 与 );
(2)计算:利用乘法公式计算每一部分的概率;
(3)求和:所求事件的概率就是各种可能情形 Ai 发生的可能性与已知在 Ai发生的条件下事件 B 发生的可能性的乘积之和,即
.
例5 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知第1,2,3台车床加工的零件分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
设B=“任取一个零件为次品”, Ai=“零件为第i台车床加工” (i=1, 2, 3), 则
解:
多个事件的全概率公式
例5 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知第1,2,3台车床加工的零件分别占总数的25%,30%,45%.
(2)如果取到的零件是次品,计算它是第1台车床加工的概率
如果取到的零件是次品,计算它是第i(i=1, 2, 3)台车床加工的概率,就是计算在B发生的条件下,事件Ai发生的概率,即
解:
“化整为零”求全概率问题
(1)已知事件 B 的发生有各种可能的情形Ai(i =1,2,3),事件 B 发生的可能性,就是各种可能情形 Ai 发生的可能性与已知在 Ai 发生的条件下事件 B 发生的可能性的乘积之和,即 .
(2)在上例中,P(Ai)是试验之前就已知的概率,它是第 i 台车床加工的零件所占的比例,称为先验概率. 当已知抽到的零件是次品( B 发生),
是这件次品来自第 i 台车床加工的可能性大小,通常称为后验概
率. 如果对加工的次品,要求操作员承担相应的责任,那么 , , 就分别是第1,2,3台车床操作员应承担的份额.
将上例中的问题一般化,就可以得到贝叶斯公式.
贝叶斯公式:设A1,A2,...,An是一组两两互斥的事件,
,且 ,则对任意的事件 ,
,有
注意:选讲内容,不作考试要求。
例6 在数字通信中,信号是由数字0和1组成的序列. 由于随机因素的
干扰,发送的信号0或1有可能被错误地接收为1或0. 已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
解:
解:
1. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题
完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
设A=“选到有思路的题”, B=“选到的题做对”, 则由全概率公式, 可得
解:
2. 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
设A=“取到合格品”, Bi=“取到的产品来自第i批”(i=1, 2), 则
课堂小结:
1. 全概率公式:
2. 贝叶斯公式:
