第五单元 第3课时 三角形三条边的关系(课件)-四年级数学下册人教版(共34张PPT)
文档属性
| 名称 | 第五单元 第3课时 三角形三条边的关系(课件)-四年级数学下册人教版(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 15:06:05 | ||
图片预览








文档简介
(共34张PPT)
第3课时
三角形三条边的关系
小学数学·四年级(下)·RJ
根据三角形三边的关系解释生活中的现象,提高运用数学知识解决实际问题的能力;提高观察、思考、抽象概括能力和动手操作能力。
通过摆一摆、比一比、算一算等数学活动,探究三角形三边的关系,知道三角形任意两边的和大于第三边。
积极参与探究活动,在活动中获得成功的体验,产生学习的兴趣。
探索发现三角形任意两边的和大于第三边。
灵活运用三角形三边关系解决一些数学问题。
联系已有的生活经验,通过实际操作、探究,培养学生观察、实验和操作能力及应用数学知识解决简单实际问题的能力。
三根
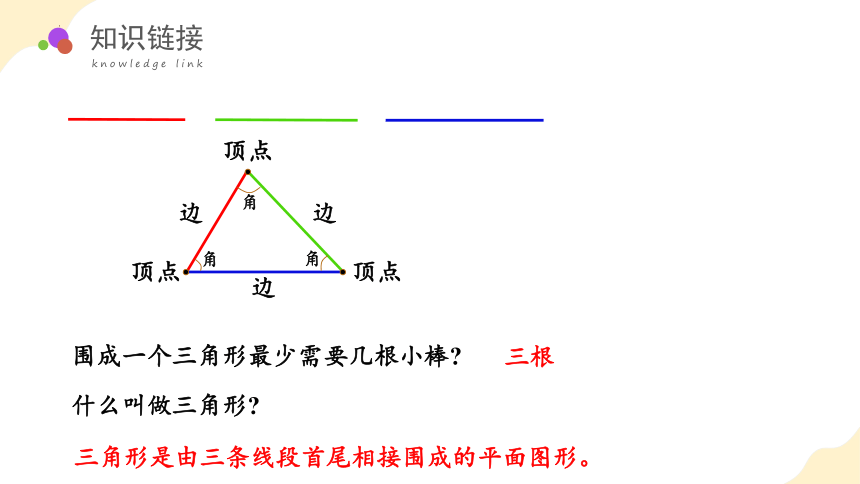
围成一个三角形最少需要几根小棒
什么叫做三角形
三角形是由三条线段首尾相接围成的平面图形。
顶点
顶点
顶点
边
边
边
角
角
角
探究两点间的距离。
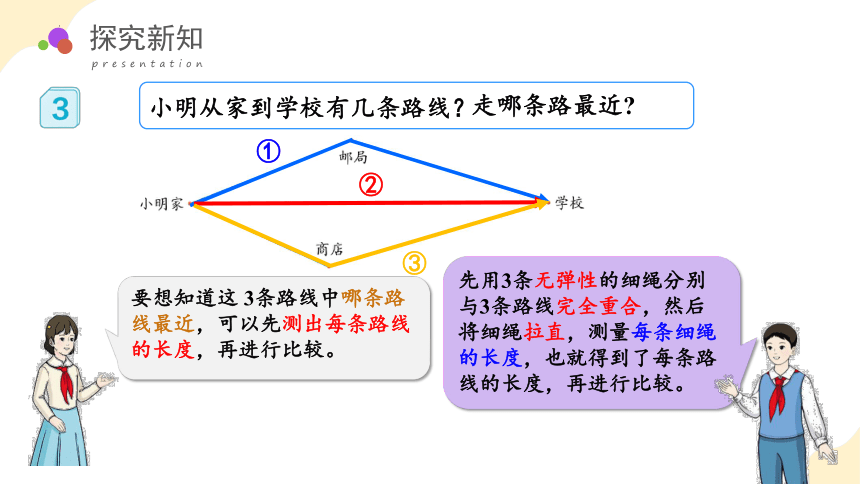
小明从家到学校有几条路线?
①
②
③
走哪条路最近
要想知道这 3条路线中哪条路线最近,可以先测出每条路线的长度,再进行比较。
先用3条无弹性的细绳分别与3条路线完全重合,然后将细绳拉直,测量每条细绳的长度,也就得到了每条路线的长度,再进行比较。
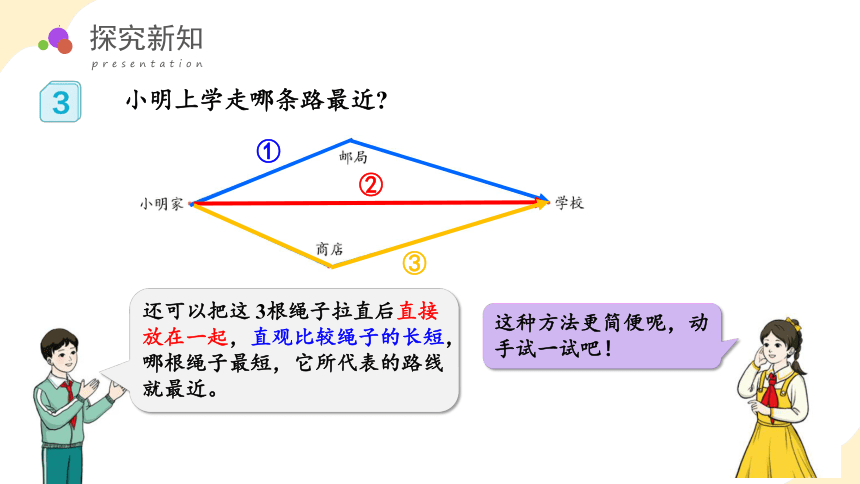
小明上学走哪条路最近
①
②
③
还可以把这 3根绳子拉直后直接放在一起,直观比较绳子的长短,哪根绳子最短,它所代表的路线就最近。
这种方法更简便呢,动手试一试吧!
如下图,先把折线和曲线都拉成直线,再比较长短。
折线
线段
曲线
通过测量、比较,发现走中间的路最近。
通过活动,你能得出什么结论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
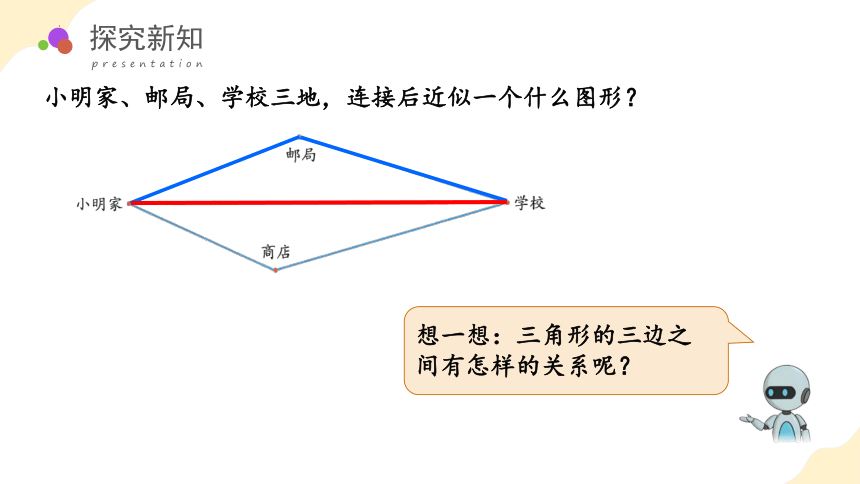
小明家、邮局、学校三地,连接后近似一个什么图形?
想一想:三角形的三边之间有怎样的关系呢?
探索发现三角形任意两边的和大于第三边。
什么样的3条线段能围成三角形呢?我们来做个实验。剪出下面 4 组纸条(单位:cm)。
(1)6、7、8;
(2)4、5、9;
(3)3、6、10;
(4)8、11、11。
用每组纸条围三角形。看看能否围成三角形,并把数据记录在表格上。
讨论:你发现了什么问题?为什么会出现这个问题?
并不是任意三个纸条都能拼成一个三角形。
“三角形三边关系”实验记录单
能摆成三角形 不能摆成三角形 编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm) 编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1) (2)
(4) (3)
你发现了什么? 6
7
8
8
11
11
4
5
9
3
6
10
(1) 6、7、8。(单位:cm)
6 cm
7 cm
8 cm
6 cm
7 cm
8 cm
6+7>8
6+8>7
8+7>6
任意两边和大于第三边,可以摆成三角形。
(2) 4、5、9。(单位:cm)
4 cm
5 cm
9 cm
4 cm
5 cm
9 cm
4+5=9
4+9>5
9+5>4
有两边的和等于第三边,摆不成三角形。
(3) 3、6、10。(单位:cm)
3 cm
6 cm
10 cm
3 cm
6 cm
10 cm
3+6<10
6+10>3
3+10>6
有两边的和小于第三边,摆不成三角形。
(4) 8、11、11。(单位:cm)
8 cm
11 cm
8 cm
11 cm
11 cm
11 cm
8+11>11
11+11>8
任意两边和大于第三边,可以摆成三角形。
(1)两点间线段长度小于曲线长度。
(2)三角形中两边的和大于第三边。
用今天学过的知识说一说为什么中间的路线最短。
归纳总结
比较不能拼出三角形的纸条的长度,你发现了什么?
发现:有两个纸条长度之和小于或等于第三个纸条的长度,就拼不出三角形。
4 cm
5 cm
9 cm
3 cm
6 cm
10 cm
5+4=9
6+3<10
9+5>4
9+4>5
10+6>3
10+3>6
6 cm
7 cm
8 cm
比较能拼出三角形的纸条的长度,你发现了什么?
6+7>8
8+11>11
8+7>6
8+6>7
11+11>8
发现:任意两个纸条的长度之和大于第三个 纸条的长度,才能拼出三角形。
8 cm
11 cm
11 cm
(1)6、7、8
(2)4、5、9
(4)8、11、11
6+7>8
6+8>7
7+8>6
8+11>11
11+11>8
4+5=9
4+9>5
5+9>4
3+6<10
3+10>6
6+10>3
8+11>11
结
论
三角形任意两边的和大于第三边。
(3)3、6、10
任意两个纸条的长度之和大于第三个 纸条的长度,才能拼出三角形。
有两个纸条长度之和小于或等于第三个纸条的长度,就拼不出三角形。
(1)6、7、8
(2)4、5、9
(4)8、11、11
8-7<6
8-6<7
7-6<8
11-11<8
5-4<9
9-4=5
9-5=4
6-3<10
10-3>6
10-6>3
11-8<11
结
论
(3)3、6、10
三角形任意两边的差小于第三边。
当任意两个纸条的长度差小于第三个纸条的长度,才能拼出三角形。
当有两个纸条的长度差大于或等于第三个纸条的长度,不能拼出三角形。
想一想,说一说:在认识三角形三边关系过程中,有哪些注意事项?
快速判断3条线段能否摆成三角形:把较短的两条线段相加的和与最长的线段相比较,若大于最长的线段,则能摆成三角形,反之则不能。
三角形任意一条边的长度都小于另外两条边的长度和,都大于另外两条边的长度差。
达标练习,巩固成果
1.李叔叔要从邮局去学校,走哪条路最近?
学校
图书馆
体育馆
邮局
教材第64页“练习十五”第5题
2.在能围成三角形的各组小棒下面画“√”(单位:cm)。
√
√
√
用两条最短边相加跟长边进行比较,最快。
3+4>5
3+3>3
2+2<6
3+3>5
3.用下面 6 根小棒,你能围出几种三角形(单位:cm)?
4种
2+2<5
2+2<6
2+5>6
2+6>6
5+6>6
6+6>6
4.下面的说法对吗?正确的画“√”,错误的画“×”。
(1)三根同样长的小棒一定能围成一个三角形。( ) (2)三角形中任意两条边的和一定大于或等于第三边。( )
(3)两点之间的所有连线中,线段最短。 ( )
(4)三角形有两条边都是 4 cm,那么第三边一定大于 4 cm。( )(5)用2 cm,6 cm和4 cm长的三根小棒可以拼成一个三角形。 ( )
√
√
5.选择。 (将正确答案的序号填在括号里)
(1)一个三角形的两条边分别是 4cm、5cm。下列选项中能作为第三条边的是( )。
A.8cm B.9cm C.11cm
A
(2)下面第( )组的三条线段能围成三角形。 (单位:cm)
3
4
5
2
3
5
5
1
3
A
B
C
A
6.一个三角形的两条边分别是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
第三条边最短是:10-5+1=6(厘米)
第三条边最长是:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
三角形三边的关系可知:10-5<第三边<10+5
5<第三边<15
三角形三边的关系
2.三角形任意两边之和大于第三边。
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
3.判断3条线段能否围成三角形,只需要判断两条短边的和是否大于第三边,如果大于就能围成三角形,反之则不能。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第3课时
三角形三条边的关系
小学数学·四年级(下)·RJ
根据三角形三边的关系解释生活中的现象,提高运用数学知识解决实际问题的能力;提高观察、思考、抽象概括能力和动手操作能力。
通过摆一摆、比一比、算一算等数学活动,探究三角形三边的关系,知道三角形任意两边的和大于第三边。
积极参与探究活动,在活动中获得成功的体验,产生学习的兴趣。
探索发现三角形任意两边的和大于第三边。
灵活运用三角形三边关系解决一些数学问题。
联系已有的生活经验,通过实际操作、探究,培养学生观察、实验和操作能力及应用数学知识解决简单实际问题的能力。
三根
围成一个三角形最少需要几根小棒
什么叫做三角形
三角形是由三条线段首尾相接围成的平面图形。
顶点
顶点
顶点
边
边
边
角
角
角
探究两点间的距离。
小明从家到学校有几条路线?
①
②
③
走哪条路最近
要想知道这 3条路线中哪条路线最近,可以先测出每条路线的长度,再进行比较。
先用3条无弹性的细绳分别与3条路线完全重合,然后将细绳拉直,测量每条细绳的长度,也就得到了每条路线的长度,再进行比较。
小明上学走哪条路最近
①
②
③
还可以把这 3根绳子拉直后直接放在一起,直观比较绳子的长短,哪根绳子最短,它所代表的路线就最近。
这种方法更简便呢,动手试一试吧!
如下图,先把折线和曲线都拉成直线,再比较长短。
折线
线段
曲线
通过测量、比较,发现走中间的路最近。
通过活动,你能得出什么结论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
小明家、邮局、学校三地,连接后近似一个什么图形?
想一想:三角形的三边之间有怎样的关系呢?
探索发现三角形任意两边的和大于第三边。
什么样的3条线段能围成三角形呢?我们来做个实验。剪出下面 4 组纸条(单位:cm)。
(1)6、7、8;
(2)4、5、9;
(3)3、6、10;
(4)8、11、11。
用每组纸条围三角形。看看能否围成三角形,并把数据记录在表格上。
讨论:你发现了什么问题?为什么会出现这个问题?
并不是任意三个纸条都能拼成一个三角形。
“三角形三边关系”实验记录单
能摆成三角形 不能摆成三角形 编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm) 编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1) (2)
(4) (3)
你发现了什么? 6
7
8
8
11
11
4
5
9
3
6
10
(1) 6、7、8。(单位:cm)
6 cm
7 cm
8 cm
6 cm
7 cm
8 cm
6+7>8
6+8>7
8+7>6
任意两边和大于第三边,可以摆成三角形。
(2) 4、5、9。(单位:cm)
4 cm
5 cm
9 cm
4 cm
5 cm
9 cm
4+5=9
4+9>5
9+5>4
有两边的和等于第三边,摆不成三角形。
(3) 3、6、10。(单位:cm)
3 cm
6 cm
10 cm
3 cm
6 cm
10 cm
3+6<10
6+10>3
3+10>6
有两边的和小于第三边,摆不成三角形。
(4) 8、11、11。(单位:cm)
8 cm
11 cm
8 cm
11 cm
11 cm
11 cm
8+11>11
11+11>8
任意两边和大于第三边,可以摆成三角形。
(1)两点间线段长度小于曲线长度。
(2)三角形中两边的和大于第三边。
用今天学过的知识说一说为什么中间的路线最短。
归纳总结
比较不能拼出三角形的纸条的长度,你发现了什么?
发现:有两个纸条长度之和小于或等于第三个纸条的长度,就拼不出三角形。
4 cm
5 cm
9 cm
3 cm
6 cm
10 cm
5+4=9
6+3<10
9+5>4
9+4>5
10+6>3
10+3>6
6 cm
7 cm
8 cm
比较能拼出三角形的纸条的长度,你发现了什么?
6+7>8
8+11>11
8+7>6
8+6>7
11+11>8
发现:任意两个纸条的长度之和大于第三个 纸条的长度,才能拼出三角形。
8 cm
11 cm
11 cm
(1)6、7、8
(2)4、5、9
(4)8、11、11
6+7>8
6+8>7
7+8>6
8+11>11
11+11>8
4+5=9
4+9>5
5+9>4
3+6<10
3+10>6
6+10>3
8+11>11
结
论
三角形任意两边的和大于第三边。
(3)3、6、10
任意两个纸条的长度之和大于第三个 纸条的长度,才能拼出三角形。
有两个纸条长度之和小于或等于第三个纸条的长度,就拼不出三角形。
(1)6、7、8
(2)4、5、9
(4)8、11、11
8-7<6
8-6<7
7-6<8
11-11<8
5-4<9
9-4=5
9-5=4
6-3<10
10-3>6
10-6>3
11-8<11
结
论
(3)3、6、10
三角形任意两边的差小于第三边。
当任意两个纸条的长度差小于第三个纸条的长度,才能拼出三角形。
当有两个纸条的长度差大于或等于第三个纸条的长度,不能拼出三角形。
想一想,说一说:在认识三角形三边关系过程中,有哪些注意事项?
快速判断3条线段能否摆成三角形:把较短的两条线段相加的和与最长的线段相比较,若大于最长的线段,则能摆成三角形,反之则不能。
三角形任意一条边的长度都小于另外两条边的长度和,都大于另外两条边的长度差。
达标练习,巩固成果
1.李叔叔要从邮局去学校,走哪条路最近?
学校
图书馆
体育馆
邮局
教材第64页“练习十五”第5题
2.在能围成三角形的各组小棒下面画“√”(单位:cm)。
√
√
√
用两条最短边相加跟长边进行比较,最快。
3+4>5
3+3>3
2+2<6
3+3>5
3.用下面 6 根小棒,你能围出几种三角形(单位:cm)?
4种
2+2<5
2+2<6
2+5>6
2+6>6
5+6>6
6+6>6
4.下面的说法对吗?正确的画“√”,错误的画“×”。
(1)三根同样长的小棒一定能围成一个三角形。( ) (2)三角形中任意两条边的和一定大于或等于第三边。( )
(3)两点之间的所有连线中,线段最短。 ( )
(4)三角形有两条边都是 4 cm,那么第三边一定大于 4 cm。( )(5)用2 cm,6 cm和4 cm长的三根小棒可以拼成一个三角形。 ( )
√
√
5.选择。 (将正确答案的序号填在括号里)
(1)一个三角形的两条边分别是 4cm、5cm。下列选项中能作为第三条边的是( )。
A.8cm B.9cm C.11cm
A
(2)下面第( )组的三条线段能围成三角形。 (单位:cm)
3
4
5
2
3
5
5
1
3
A
B
C
A
6.一个三角形的两条边分别是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
第三条边最短是:10-5+1=6(厘米)
第三条边最长是:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
三角形三边的关系可知:10-5<第三边<10+5
5<第三边<15
三角形三边的关系
2.三角形任意两边之和大于第三边。
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
3.判断3条线段能否围成三角形,只需要判断两条短边的和是否大于第三边,如果大于就能围成三角形,反之则不能。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
