第十七章 勾股定理 复习课件(15张PPT)
文档属性
| 名称 | 第十七章 勾股定理 复习课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 10:22:52 | ||
图片预览






文档简介
(共15张PPT)
勾股定理小结复习
人教版八年级下册
知识回顾
1.如果直角三角形两直角边分别为a,b,斜边
为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
知识回顾
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
针对训练
1.Rt△ABC中,斜边BC=2,则 的值为
A.8 B.4 C.6 D.无法计算
3.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为___________.
13或5
2.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6
C.3,4,5 D.7,8,9
()
c
A
针对训练
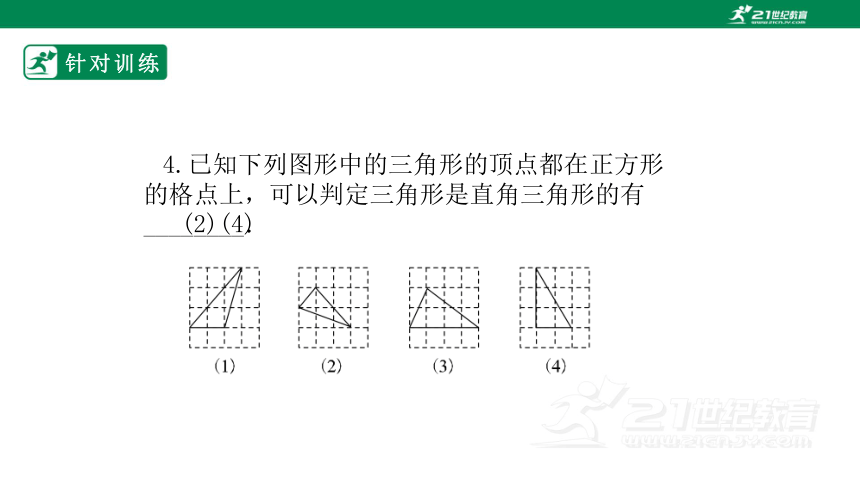
4.已知下列图形中的三角形的顶点都在正方形的格点上,可以判定三角形是直角三角形的有________.
(2)(4)
折叠问题
5. 如图,在长方形ABCD中,AB=3cm,AD=9cm将此长方形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
解:∵长方形折叠,使点B与点D重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
针对训练
6.如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕是DE,则CD的长为 .
1.75cm
最短路径问题
如图,一个牧童想把他的牛先带到小河边去饮水,然后回家.牧童现在在A处,他家在B处,A,B两地到河岸的距离分别为1km和3km,B与C两地的距离.为3km.他要完成这件事情需要走的最短路程是多少
例一
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值是( )
A.8 B.9 C.10 D.12
C
例二
A
D
B
C
N
M
立体图形中的最短路径问题
例三
有一个圆柱,它的高为12cm,底面半径为3cm,在圆拄下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,沿圆柱侧面爬行的最短路程是(π取3) 。
A
B
15
正方体中的最值问题
分析:关键是把正方体展开成平面图形.
根据“两点之间线段最短”,即可求得最短线路.
B
例四
长方体中的最值问题
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短 最短路线长为多少
分析:
爬行路线有三种情况,需全方位考虑展平的情况.
例五
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
勾股定理小结复习
人教版八年级下册
知识回顾
1.如果直角三角形两直角边分别为a,b,斜边
为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
知识回顾
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
针对训练
1.Rt△ABC中,斜边BC=2,则 的值为
A.8 B.4 C.6 D.无法计算
3.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为___________.
13或5
2.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6
C.3,4,5 D.7,8,9
()
c
A
针对训练
4.已知下列图形中的三角形的顶点都在正方形的格点上,可以判定三角形是直角三角形的有________.
(2)(4)
折叠问题
5. 如图,在长方形ABCD中,AB=3cm,AD=9cm将此长方形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
解:∵长方形折叠,使点B与点D重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
针对训练
6.如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕是DE,则CD的长为 .
1.75cm
最短路径问题
如图,一个牧童想把他的牛先带到小河边去饮水,然后回家.牧童现在在A处,他家在B处,A,B两地到河岸的距离分别为1km和3km,B与C两地的距离.为3km.他要完成这件事情需要走的最短路程是多少
例一
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值是( )
A.8 B.9 C.10 D.12
C
例二
A
D
B
C
N
M
立体图形中的最短路径问题
例三
有一个圆柱,它的高为12cm,底面半径为3cm,在圆拄下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,沿圆柱侧面爬行的最短路程是(π取3) 。
A
B
15
正方体中的最值问题
分析:关键是把正方体展开成平面图形.
根据“两点之间线段最短”,即可求得最短线路.
B
例四
长方体中的最值问题
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短 最短路线长为多少
分析:
爬行路线有三种情况,需全方位考虑展平的情况.
例五
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
