一元二次方程及解法[上学期]
图片预览







文档简介
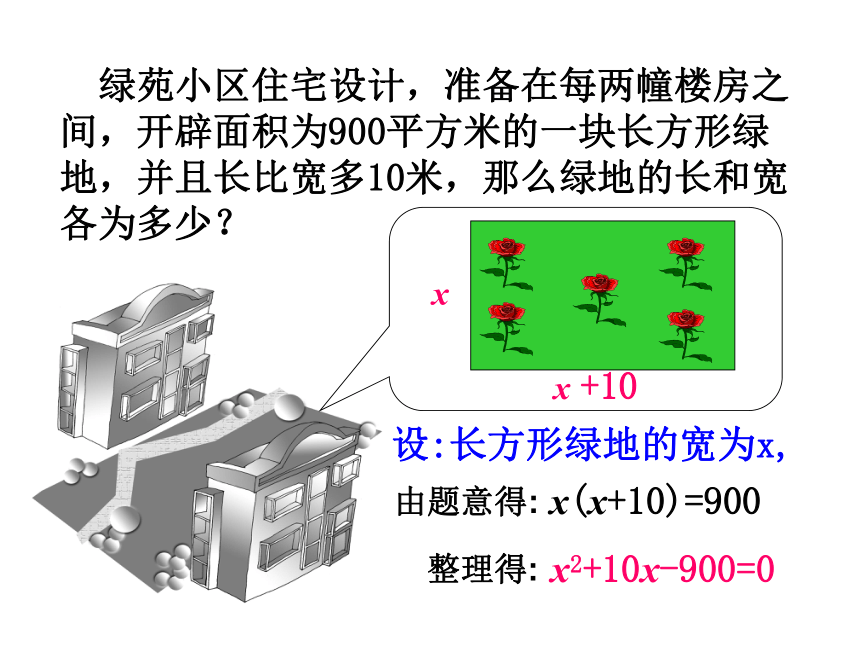
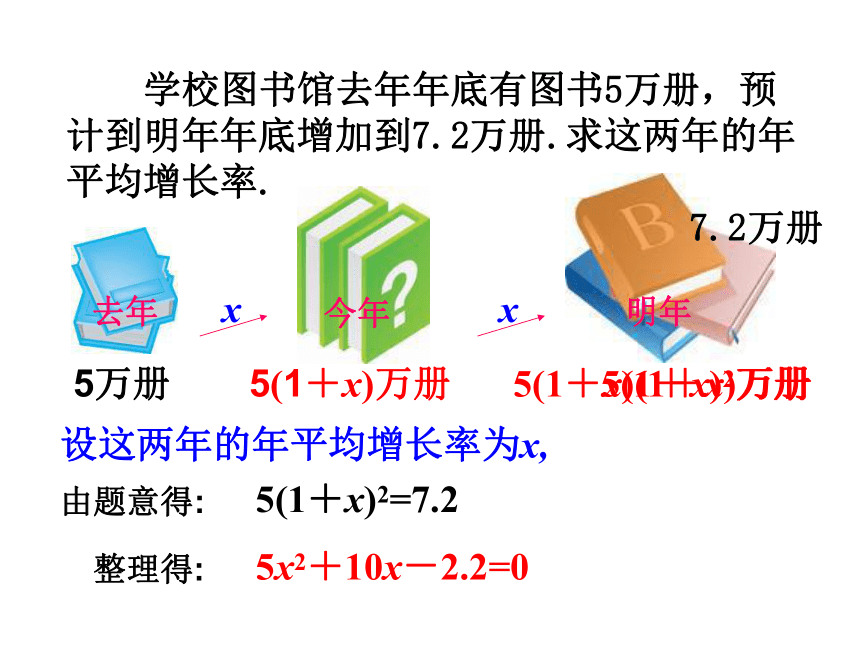
课件29张PPT。 绿苑小区住宅设计,准备在每两幢楼房之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?设:长方形绿地的宽为x,xx +10x(x+10)=900x2+10x-900=0由题意得:整理得: 学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.设这两年的年平均增长率为x, 去年今年明年5万册5(1+x)万册5(1+x)(1+x)万册xx由题意得:整理得:5(1+x)2=7.2 5x2+10x-2.2=0 5(1+x)2万册7.2万册x2+10x-900=0 (1)5x2+10x-2.2=0 (2)思考、讨论 这两个方程都是不是一元一次方程?
那么这两个方程与一元一次方程的区别在哪里?
它们有什么共同特点呢? 共同特点:
(1) 都是整式方程
(2) 只含有一个未知数
区别: 未知数的最高次数是2 只含有一个未知数,并且未知数的最高次数是2,这样的方程叫做一元二次方程. 一元二次x2+10x-900=0 (1)5x2+10x-2.2=0 (2)思考、讨论 只含有一个未知数,并且未知数的最高次数是2,这样的方程叫做一元二次方程. 通常可写成如下的一般形式: ax2+bx+c=0 其中a、b、c分别叫做二次项系数、一次项系数和常数项.1.下列方程中哪些是一元二次方程?(a≠0)2.将下列方程化为一般形式,并分别指出它们的二次项系数、一次项系数和常数项: 3.关于x的方程mx2-3x=x2-mx+2是一元二次方程的条件是什么?4.关于x的一元二次方程(m-2)x2+3x+m2-4=0有一个解是0,求m的值.一元二次方程的解法(一)试一试:解下列方程,并说明你所用的方法,与同伴交流.
(1)x2=4; (2)(x+1)2=81;这种方法叫做直接开平方法.解:(1)开平方,得:
X=±2(2) 开平方,得:
x+1=±3∴原方程的解为
x1=2,x2=-4∴原方程的解为
x= ±2 形如 (a≠0)的一 元二次方程的解法:当b≧ 0时 ,当b< 0 时 ,此方程无实数解.直接开平方法解下列方程:(1) y2=5 ; (2)4(x+3)2=12;(3) x2-100=0 ; (4)(2x+3)2-25=0;解:将方程左边分解因式 得 (x-10)(x+10)=0x-10=0或x+10=0∴x1=10, x2=-10解:将方程左边分解因式 得 (2x-2)(2x+8)=02x-2=0或2x+8=0∴x1=1, x2=-4这种方法叫做因式分解法.解下列方程:(3)3x2+2x=0; (4)x2= 3x .(1)16x2-25=0 ; (2)x2- 4x +4=0;注意:用因式分解法解一元二次方程,先要把方程化为一般形式,即等式的一边为0.练 习
解下列方程(课本P30 练习 1)
(1)x2=169; (2)45-x2=0;
(3)12y2-25=0; (4)x2-2x=0;
(5)(t-2)(t+1)=0; (6)x(x+1)-5x=0.2.解下列方程:3.小明在解方程x2=3x时,将方程两边同时除以x,得x=3,这样做法对吗?为什么?作业:一、用直接开平方法解下列方程:(1)x2-16=0 (2)x2-32=0
(3)3x2 - =0 (4)2y2=
(5) 9(5x+1)2=49
(6) 5(2x-1)2=4(2x-1)2+9二、用因式分解法解下列方程:(1)4x2-121=0 (2)5x2+x = x2+2x
(3)(x+1)2+3(x+1)=0 (4) 2x(3x-1)=5(3x-1)今天我们学到了……一元一次方程的有关概念一元一次方程的一般形式:ax2+bx+c=0 (a≠0)一元一次方程的解法:直接开平方法因式分解法例1、方程 是否为一元二次方程?如果不是,说明理由;如果是,指出它的二次项、一次项系数及常数项. 解:去括号,得 3x2-3x=2x+4+8.
移项,得 3x2-3x-2x-4-8=0.
合并同类项,得 3x2-5x-12=0.
∴原方程是一元二次方程;二次项系数是3,一次项系数是 - 5,常数项是 – 12.一元二次方程的解法(二)一、复习旧知,提出问题:1.解下列方程,并说明所用的方法。(1)3-2x2=1 (2)(x+1)2-6=0 (3)(x-2)2-1=0 2.请说出完全平方公式。(x+a)2=(x-a)2=x2+2ax+a2x2-2ax+a23.你能解以下方程吗?(1)x2+2x=5 (2)x2-4x+3=0都可化为x2=b(b≧0)或(x-a)2=b(b≧0)今天我们要研究二次项系数为1的一般形式的一元二次方程的解法。二、探究方程解法:问题1:对于方程(1)x2+2x=5 (2)x2- 4x+3=0能否经过适当的变形,将它们转化为( )2=b的形式,应用直接开方法求解呢?问题2:把方程x2+2x=5变形为(x+1)2=6,把方程x2-4x+3=0变形为(x-2) 2=1,方程的左边和右边各有什么特征?可以用什么方法求解?方程的左边是一个含有未知数的_________,右边是一个_______,可以用直接开平方法求解。这种解一元二次方程的方法叫做_______。配方法非负数完全平方式三、例题:例1.用配方法解下列方程:(1)x2-6x-7=0 (2)x2+3x+1=0例2.如何用配方法解下列方程? (1) 4x2-12x-1=0
(2) 3x2+2x-3=0课堂小结:配方法解一元二次方程的步骤:1、把常数项移到等号右边,方程两边同除以二次项系数,使新方程的二次项系数为1;2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;3、如果方程的右边整理后是非负数,用直接开平方法求解;如果右边是个负数,则原方程无实根。四、课堂练习:课本P33 练习1、2。五、作业:一、填空:1. x2-2x+____=(x- )2 2. x2+16+____=(x+ )23. y2+5y+____=(y+ )2 4. 2x2-5x+____=2(x- )2二、用配方法解下列方程:1. x2-10x-11=02. x2-5x+6=03. x2-4x+7=04. x2+6x+7=0三、用配方法解下列方程:1. 4x2+4x+1=02. 9x2-6x+1=03. 2x2-x-1=04. 5x2-4x-1=0一元二次方程的解法(三)一、复习旧知,提出问题2.用配方法解一元二次方程的步骤是什么?3.用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一个更直接的方法,迅速求得一元二次方程的实数根呢?二、探索问题的解决方法:问题3:在研究了问题1和问题2后,你能得出方程
ax2+bx+c=0的根吗?当b2- 4ac<0时的情况呢?这个公式说明一元二次方程的根是由方程的系数所确定的,利用这个公式,我们可以由一元二次方程中的系数a,b,c的值直接求得方程的根。这种解一元二次方程方程的方法叫做公式法。三、例题:例1、解下列方程:
(1)2x2+x-6=0 (2)x2+4x=2 (3) 5x2-4x-12=0
(4)4x2+4x+10=1-8x (5)x2-x+1=0四、课堂练习:P35练习五、知识扩展:一元二次方程根的判别式我们在一元二次方程的配方过中得到: 发现只有当b2-4ac≥0时,才能直接开平方,
得:也就是说,一元二次方程ax2+bx+c=0(a≠0)只有当系数a、b、c满足条件b2-4ac≥0时才有实数根.我们不难发现一元二次方程的根有三种情况: 当b2-4ac>0时,方程有两个不相等的实数根;③当b2-4ac<0时,方程没有实数根.这里的b2-4ac叫做一元二次方程的根的判别式,
用它可以直接判断一个一元二次方程是否有实数根. 新题型:
应用判别式来确实方程中的待定系数 练习1:不解方程,判别下列方程根的情况.①2x2+3x-4=0 ②16y2+9=24y
③x2+1=-x ④ 5(x2+1)-7x=0六、作业:2、用适当的方法解下列方程:配方法解一元二次方程的步骤:1、把常数项移到等号右边,方程两边同除以二次项系数,使新方程的二次项系数为1;2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;3、如果方程的右边整理后是非负数,用直接开平方法求解;如果右边是个负数,则原方程无实根。
那么这两个方程与一元一次方程的区别在哪里?
它们有什么共同特点呢? 共同特点:
(1) 都是整式方程
(2) 只含有一个未知数
区别: 未知数的最高次数是2 只含有一个未知数,并且未知数的最高次数是2,这样的方程叫做一元二次方程. 一元二次x2+10x-900=0 (1)5x2+10x-2.2=0 (2)思考、讨论 只含有一个未知数,并且未知数的最高次数是2,这样的方程叫做一元二次方程. 通常可写成如下的一般形式: ax2+bx+c=0 其中a、b、c分别叫做二次项系数、一次项系数和常数项.1.下列方程中哪些是一元二次方程?(a≠0)2.将下列方程化为一般形式,并分别指出它们的二次项系数、一次项系数和常数项: 3.关于x的方程mx2-3x=x2-mx+2是一元二次方程的条件是什么?4.关于x的一元二次方程(m-2)x2+3x+m2-4=0有一个解是0,求m的值.一元二次方程的解法(一)试一试:解下列方程,并说明你所用的方法,与同伴交流.
(1)x2=4; (2)(x+1)2=81;这种方法叫做直接开平方法.解:(1)开平方,得:
X=±2(2) 开平方,得:
x+1=±3∴原方程的解为
x1=2,x2=-4∴原方程的解为
x= ±2 形如 (a≠0)的一 元二次方程的解法:当b≧ 0时 ,当b< 0 时 ,此方程无实数解.直接开平方法解下列方程:(1) y2=5 ; (2)4(x+3)2=12;(3) x2-100=0 ; (4)(2x+3)2-25=0;解:将方程左边分解因式 得 (x-10)(x+10)=0x-10=0或x+10=0∴x1=10, x2=-10解:将方程左边分解因式 得 (2x-2)(2x+8)=02x-2=0或2x+8=0∴x1=1, x2=-4这种方法叫做因式分解法.解下列方程:(3)3x2+2x=0; (4)x2= 3x .(1)16x2-25=0 ; (2)x2- 4x +4=0;注意:用因式分解法解一元二次方程,先要把方程化为一般形式,即等式的一边为0.练 习
解下列方程(课本P30 练习 1)
(1)x2=169; (2)45-x2=0;
(3)12y2-25=0; (4)x2-2x=0;
(5)(t-2)(t+1)=0; (6)x(x+1)-5x=0.2.解下列方程:3.小明在解方程x2=3x时,将方程两边同时除以x,得x=3,这样做法对吗?为什么?作业:一、用直接开平方法解下列方程:(1)x2-16=0 (2)x2-32=0
(3)3x2 - =0 (4)2y2=
(5) 9(5x+1)2=49
(6) 5(2x-1)2=4(2x-1)2+9二、用因式分解法解下列方程:(1)4x2-121=0 (2)5x2+x = x2+2x
(3)(x+1)2+3(x+1)=0 (4) 2x(3x-1)=5(3x-1)今天我们学到了……一元一次方程的有关概念一元一次方程的一般形式:ax2+bx+c=0 (a≠0)一元一次方程的解法:直接开平方法因式分解法例1、方程 是否为一元二次方程?如果不是,说明理由;如果是,指出它的二次项、一次项系数及常数项. 解:去括号,得 3x2-3x=2x+4+8.
移项,得 3x2-3x-2x-4-8=0.
合并同类项,得 3x2-5x-12=0.
∴原方程是一元二次方程;二次项系数是3,一次项系数是 - 5,常数项是 – 12.一元二次方程的解法(二)一、复习旧知,提出问题:1.解下列方程,并说明所用的方法。(1)3-2x2=1 (2)(x+1)2-6=0 (3)(x-2)2-1=0 2.请说出完全平方公式。(x+a)2=(x-a)2=x2+2ax+a2x2-2ax+a23.你能解以下方程吗?(1)x2+2x=5 (2)x2-4x+3=0都可化为x2=b(b≧0)或(x-a)2=b(b≧0)今天我们要研究二次项系数为1的一般形式的一元二次方程的解法。二、探究方程解法:问题1:对于方程(1)x2+2x=5 (2)x2- 4x+3=0能否经过适当的变形,将它们转化为( )2=b的形式,应用直接开方法求解呢?问题2:把方程x2+2x=5变形为(x+1)2=6,把方程x2-4x+3=0变形为(x-2) 2=1,方程的左边和右边各有什么特征?可以用什么方法求解?方程的左边是一个含有未知数的_________,右边是一个_______,可以用直接开平方法求解。这种解一元二次方程的方法叫做_______。配方法非负数完全平方式三、例题:例1.用配方法解下列方程:(1)x2-6x-7=0 (2)x2+3x+1=0例2.如何用配方法解下列方程? (1) 4x2-12x-1=0
(2) 3x2+2x-3=0课堂小结:配方法解一元二次方程的步骤:1、把常数项移到等号右边,方程两边同除以二次项系数,使新方程的二次项系数为1;2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;3、如果方程的右边整理后是非负数,用直接开平方法求解;如果右边是个负数,则原方程无实根。四、课堂练习:课本P33 练习1、2。五、作业:一、填空:1. x2-2x+____=(x- )2 2. x2+16+____=(x+ )23. y2+5y+____=(y+ )2 4. 2x2-5x+____=2(x- )2二、用配方法解下列方程:1. x2-10x-11=02. x2-5x+6=03. x2-4x+7=04. x2+6x+7=0三、用配方法解下列方程:1. 4x2+4x+1=02. 9x2-6x+1=03. 2x2-x-1=04. 5x2-4x-1=0一元二次方程的解法(三)一、复习旧知,提出问题2.用配方法解一元二次方程的步骤是什么?3.用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一个更直接的方法,迅速求得一元二次方程的实数根呢?二、探索问题的解决方法:问题3:在研究了问题1和问题2后,你能得出方程
ax2+bx+c=0的根吗?当b2- 4ac<0时的情况呢?这个公式说明一元二次方程的根是由方程的系数所确定的,利用这个公式,我们可以由一元二次方程中的系数a,b,c的值直接求得方程的根。这种解一元二次方程方程的方法叫做公式法。三、例题:例1、解下列方程:
(1)2x2+x-6=0 (2)x2+4x=2 (3) 5x2-4x-12=0
(4)4x2+4x+10=1-8x (5)x2-x+1=0四、课堂练习:P35练习五、知识扩展:一元二次方程根的判别式我们在一元二次方程的配方过中得到: 发现只有当b2-4ac≥0时,才能直接开平方,
得:也就是说,一元二次方程ax2+bx+c=0(a≠0)只有当系数a、b、c满足条件b2-4ac≥0时才有实数根.我们不难发现一元二次方程的根有三种情况: 当b2-4ac>0时,方程有两个不相等的实数根;③当b2-4ac<0时,方程没有实数根.这里的b2-4ac叫做一元二次方程的根的判别式,
用它可以直接判断一个一元二次方程是否有实数根. 新题型:
应用判别式来确实方程中的待定系数 练习1:不解方程,判别下列方程根的情况.①2x2+3x-4=0 ②16y2+9=24y
③x2+1=-x ④ 5(x2+1)-7x=0六、作业:2、用适当的方法解下列方程:配方法解一元二次方程的步骤:1、把常数项移到等号右边,方程两边同除以二次项系数,使新方程的二次项系数为1;2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;3、如果方程的右边整理后是非负数,用直接开平方法求解;如果右边是个负数,则原方程无实根。
