一元二次方程[上学期]
图片预览








文档简介
课件22张PPT。一元二次方程引 入一般形式定 义巩固练习1例 题巩固练习2小 结主讲:陈志兴问题: 建造一个面积为20平方米,长比宽多 1 米的长方形花坛,问它的宽是多少?解:设这个花坛的宽为x米,x则长为(x+1)米,x+1根据题意得:
x ( x+1) = 20
即 x 2 + x - 20 = 0一元二次方程首页观察方程 ①等号两边都是整式 ②又只含有一个未知数 ③并且未知数的最高次数是2
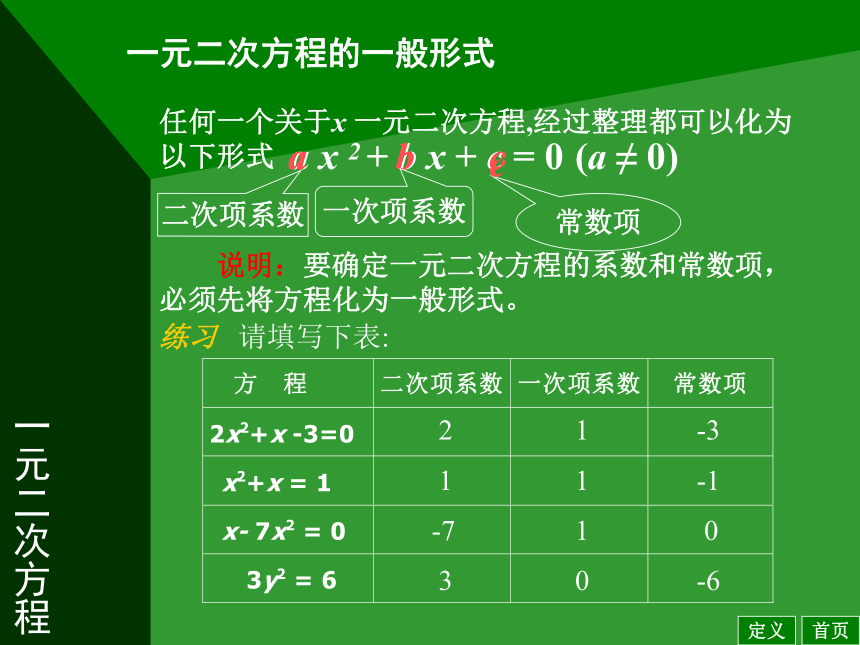
这样的方程叫一元二次方程特征如下:有何特征?一元二次方程请判断下列方程是否为一元二次方程:练习 (4) 3z2+1 = z (2z2 - 1)(5) x 2 = 0以上方程中(1)、(3)、(4)不是一元二次方程(6) ( x + 2) 2 = 4首页一元二次方程 一元二次方程的一般形式任何一个关于x 一元二次方程,经过整理都可以化为以下形式 a x 2 + b x + c = 0(a ≠ 0)二次项系数aaabbb一次项系数常数项ccc练习请填写下表:21-311-1-71030-6 说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式。首页定义一元二次方程巩固练习:选择题((A) 5 (B) -5+(C)(D) 0A填空题 方程 3x ( x+2) = 11+2(3x-5)的二次项系数、一次项系数与常数项的积是3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x2 + 6x = 11 + 6x -103x2 + 6x - 6x-11 +10 = 03x2 -1 = 0二次项系数为3,常数项为-1,一次项系数为00000000首页一元二次方程解一元二次方程 求一个一元二次方程的根的过程,叫解一元二次方程。 使得一个一元二次方程方程左右两边的值相等的未知数的值叫做这个一元二次方程的根。 一元二次方程化为一般形式ax2+bx+c=0 (a≠0)后,如果它的左边的二次三项式能因式分解,那么就可以用因式分解法解这个方程。首页小结一元二次方程例 解方程:(1) x2-3x = 0解题过程首页(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案一元二次方程(1) x2-3x = 0解:把方程左边分解因式,得 x(x-3) = 0∴ x = 0 或x -3 = 0∴原方程的根是x1=0 , x2=3首页返回一元二次方程(2) 2 x2+13x -7= 0解:把方程左边分解因式,得(2x -1)(x+7) = 0∴ 2x -1 = 0 , x =0.5
或 x +7 = 0, x = -7∴原方程的根是x1=0.5 , x2= -7首页返回一元二次方程第(1)题答案:x2 = 2x
x2 -2x = 0 x(x -2) = 0x1=0 , x2=2返回一元二次方程第(2)题答案:返回3x2 - 27=0
x2 -9 = 0 (x+3)(x -3) = 0x1=-3 , x2=3x+3 = 0 或x -3 = 0=一元二次方程第(3)题答案:返回(x+4)(x -3) = 0x1=-4 , x2=3x+4= 0 或x -3=0一元二次方程第(4)题答案:返回(3x+1)(2x -1) = 0x1=? , x2=?3x+1= 0 或2x -1=0一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案(4) 6x2 - x - 1= 0答案一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案(4) 6x2 - x - 1= 0答案一元二次方程想一想观察方程 ③并且未知数的最高次数是2
这样的方程叫一元二次方程特征如下:有何特征? ①等号两边都是整式 ②又只含有一个未知数一元二次方程返回一元二次方程 一元二次方程的一般形式任何一个关于x 一元二次方程,经过整理都可以化为以下形式 a x 2 + b x + c = 0(a ≠ 0)二次项系数aaabbb一次项系数常数项ccc 说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式。返回小 结一元二次方程一元二次方程的定义
一元二次方程的一般形式
因式分解法
转化思想
123结束课后思考:
如果a是一元二次方程x2-3x+m=0的一个根,-a是一元二次方程x2 + 3x-m=0的一个根,那么a的值是多少?
x ( x+1) = 20
即 x 2 + x - 20 = 0一元二次方程首页观察方程 ①等号两边都是整式 ②又只含有一个未知数 ③并且未知数的最高次数是2
这样的方程叫一元二次方程特征如下:有何特征?一元二次方程请判断下列方程是否为一元二次方程:练习 (4) 3z2+1 = z (2z2 - 1)(5) x 2 = 0以上方程中(1)、(3)、(4)不是一元二次方程(6) ( x + 2) 2 = 4首页一元二次方程 一元二次方程的一般形式任何一个关于x 一元二次方程,经过整理都可以化为以下形式 a x 2 + b x + c = 0(a ≠ 0)二次项系数aaabbb一次项系数常数项ccc练习请填写下表:21-311-1-71030-6 说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式。首页定义一元二次方程巩固练习:选择题((A) 5 (B) -5+(C)(D) 0A填空题 方程 3x ( x+2) = 11+2(3x-5)的二次项系数、一次项系数与常数项的积是3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x ( x+2) = 11+2(3x-5)3x2 + 6x = 11 + 6x -103x2 + 6x - 6x-11 +10 = 03x2 -1 = 0二次项系数为3,常数项为-1,一次项系数为00000000首页一元二次方程解一元二次方程 求一个一元二次方程的根的过程,叫解一元二次方程。 使得一个一元二次方程方程左右两边的值相等的未知数的值叫做这个一元二次方程的根。 一元二次方程化为一般形式ax2+bx+c=0 (a≠0)后,如果它的左边的二次三项式能因式分解,那么就可以用因式分解法解这个方程。首页小结一元二次方程例 解方程:(1) x2-3x = 0解题过程首页(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案一元二次方程(1) x2-3x = 0解:把方程左边分解因式,得 x(x-3) = 0∴ x = 0 或x -3 = 0∴原方程的根是x1=0 , x2=3首页返回一元二次方程(2) 2 x2+13x -7= 0解:把方程左边分解因式,得(2x -1)(x+7) = 0∴ 2x -1 = 0 , x =0.5
或 x +7 = 0, x = -7∴原方程的根是x1=0.5 , x2= -7首页返回一元二次方程第(1)题答案:x2 = 2x
x2 -2x = 0 x(x -2) = 0x1=0 , x2=2返回一元二次方程第(2)题答案:返回3x2 - 27=0
x2 -9 = 0 (x+3)(x -3) = 0x1=-3 , x2=3x+3 = 0 或x -3 = 0=一元二次方程第(3)题答案:返回(x+4)(x -3) = 0x1=-4 , x2=3x+4= 0 或x -3=0一元二次方程第(4)题答案:返回(3x+1)(2x -1) = 0x1=? , x2=?3x+1= 0 或2x -1=0一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案(4) 6x2 - x - 1= 0答案一元二次方程例 解方程:(1) x2-3x = 0(2) 2 x2+13x -7= 0解题过程巩固练习(1) x2 = 2x答案解题过程(2) 3 x2-27 = 0答案(3) x2+x -12= 0答案(4) 6x2 - x - 1= 0答案一元二次方程想一想观察方程 ③并且未知数的最高次数是2
这样的方程叫一元二次方程特征如下:有何特征? ①等号两边都是整式 ②又只含有一个未知数一元二次方程返回一元二次方程 一元二次方程的一般形式任何一个关于x 一元二次方程,经过整理都可以化为以下形式 a x 2 + b x + c = 0(a ≠ 0)二次项系数aaabbb一次项系数常数项ccc 说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式。返回小 结一元二次方程一元二次方程的定义
一元二次方程的一般形式
因式分解法
转化思想
123结束课后思考:
如果a是一元二次方程x2-3x+m=0的一个根,-a是一元二次方程x2 + 3x-m=0的一个根,那么a的值是多少?
