一元二次方程[上学期]
图片预览









文档简介
课件35张PPT。向同行学习,向专家致敬!华师中山附中 聂少林§22.1 一元二次方程
说 课义务教育课程标准实验教科书(华师大版)教材分析教学过程分析教学评价分析教学方法分析教学重难点分析说课程序教学目标分析教学方法教学过程教学评价横向联系:学习一元二次方程对其它学科也有重要意义。目标分析重、难点教材的地位和作用主要内容之一;占有重要地位。
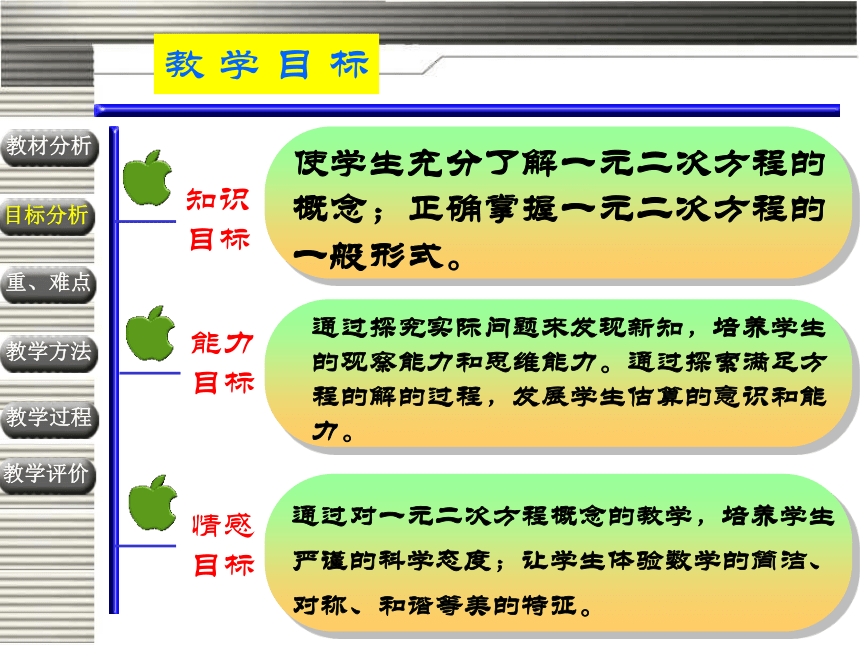
纵向发展:通过对一元二次方程的学习,可以对已学内容加以巩固,同时,又为我们学习后续内容打下基础。教材分析使学生充分了解一元二次方程的概念;正确掌握一元二次方程的一般形式。通过探究实际问题来发现新知,培养学生的观察能力和思维能力。通过探索满足方程的解的过程,发展学生估算的意识和能力。通过对一元二次方程概念的教学,培养学生
严谨的科学态度;让学生体验数学的简洁、
对称、和谐等美的特征。知识
目标能力
目标情感
目标教 学 目 标教学方法教学过程教学评价目标分析重、难点教材分析教学重点和难点重点:
一元二次方程的概念和一般形式.
教学方法教学过程教学评价目标分析重、难点教材分析难点:
正确理解和掌握一般形式中的a≠0 ,“项”和“系数” .启发式、类比法
以教师为主导、学生为主体、问题为主线
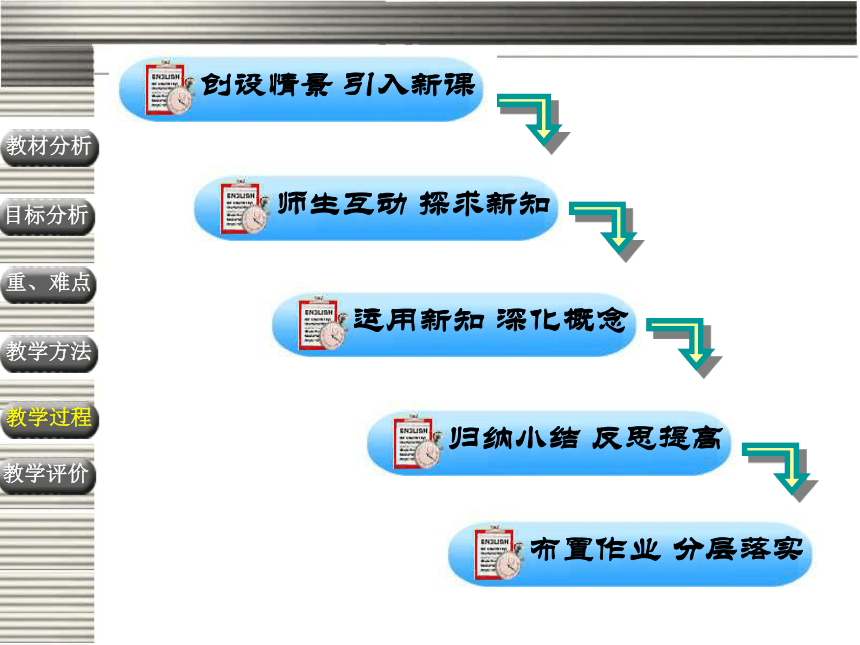
问题情景---数学模型-----概念归纳
自主探索、合作交流 教学方法教学方法教学过程教学评价目标分析重、难点教材分析 运用新知 深化概念 归纳小结 反思提高 师生互动 探求新知 布置作业 分层落实 教学方法教学过程教学评价目标分析重、难点教材分析教学过程 创设情景 引入新课 一、创设情境 引入新课问题情境:认识“老朋友” 1、你还记得什么叫方程?什么叫方程的解吗?
2、什么是一元一次方程?它的一般形式是怎样的?
3、我们知道了利用一元一次方程可以解决生活中的一些实际问题,你还记得利用一元一次方程解决实际问题的步骤吗?
创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
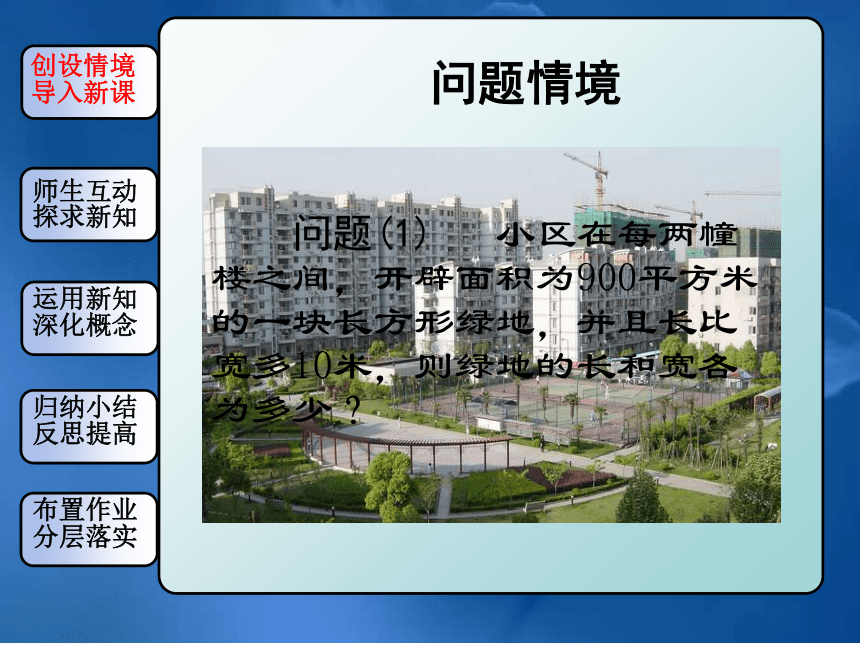
分层落实问题情境 问题(1) 小区在每两幢楼之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,则绿地的长和宽各为多少?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实问题(2) 学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的年平均增长率?创设情境
导入新课师生互动探求新知运用新知深化概念归纳小结
反思提高布置作业
分层落实(3)一个正方形的面积的2倍等于15,这个正方形的边长是多少?
(4)一个数比另一个数大3,且两个数之积为0,求这两个数。补 充 实 例创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实实 际 问 题
(1)小区在每两幢楼之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,则绿地的长和宽各为多少?
(2) 学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的年平均增长率?
(3)一个正方形的面积的2倍等于15,这个正方形的边长是多少?
(4)一个数比另一个数大3,且两个数之积为0,求这两个数。
二、师生互动 探求新知仔细观察,你会发现什么规律?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实问题:
类比一元一次方程的概念给出一元二次方程的概念:创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实①是整式方程;②只含有一个未知数;③未知数的最高次数是2. 归纳新知,形成概念创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程. 一元二次方程必须同时满足以下三个条件: 观察、思考创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 上述一元二次方程有哪些共同点
和不同点?一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。为什么要限制a≠0,b,c可以为零吗?想一想 a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实三、运用新知 体验成功 1.判断下列方程是否为一元二次方程:创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 一元二次方程的二次项系数、一次项系数和常数项.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实例:把下面的方程化为一般形式, 并写出它的二次项系数、一次项系数和常数项. 练习:课本P 27练习题1二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实类比学习:
一元二次方程的解(或根).创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实说一说:
未知数的值 x= -1,x=0,x=2
是不是方程 x2-2=x 的根.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实用试验的方法探索情景一中所列方程x(x+10)=900的解,方程有几个解?都是情景一的解吗?四、归纳小结 反思提高
本节课你最大的体验是什么? 本节课你学习了哪些知识? 回
顾
与
思
考本节课你掌握了哪些数学方法?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实五、布置作业 分层落实2、选做题:
(1)当m取何值时,方程(m-1)x3m+1+2mx+3=0是关于x的一元二次方程?
(3)已知关于x的一元二次方程a(x2-1)-2ax=x(4x-1)+1,写出它的各项系数,并指出字母a的取值范围。
(4)关于x的方程(k-1)(k+3)x2+(k-1)x-k+3=0.当k为何值时,它是一元二次方程?当k为何值时,它是一元一次方程?1、必做题:
(1)P27习题第1、2、3题;
(2)做好下节课学习内容的预习.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实让数学回归生活教法分析学法分析教学过程教学评价目标分析重难点教材分析1、本节课以以概念讲解为载体,以展示思维分析为主线,重视过程教学,从而发展学生的科学精神和创新意识,培养他们获取知识、运用知识以及运用数学语言进行交流的能力.2、在整个教学过程中,加强数学教学与信息技术教育的整合,借助计算机等多媒体教学手段,加强了学生的感性认识,也有效地激发学生学习数学的兴趣.教 学 评价敬请各位专家、老师
批评指正!再见
华师中山附中 聂少林
说 课义务教育课程标准实验教科书(华师大版)教材分析教学过程分析教学评价分析教学方法分析教学重难点分析说课程序教学目标分析教学方法教学过程教学评价横向联系:学习一元二次方程对其它学科也有重要意义。目标分析重、难点教材的地位和作用主要内容之一;占有重要地位。
纵向发展:通过对一元二次方程的学习,可以对已学内容加以巩固,同时,又为我们学习后续内容打下基础。教材分析使学生充分了解一元二次方程的概念;正确掌握一元二次方程的一般形式。通过探究实际问题来发现新知,培养学生的观察能力和思维能力。通过探索满足方程的解的过程,发展学生估算的意识和能力。通过对一元二次方程概念的教学,培养学生
严谨的科学态度;让学生体验数学的简洁、
对称、和谐等美的特征。知识
目标能力
目标情感
目标教 学 目 标教学方法教学过程教学评价目标分析重、难点教材分析教学重点和难点重点:
一元二次方程的概念和一般形式.
教学方法教学过程教学评价目标分析重、难点教材分析难点:
正确理解和掌握一般形式中的a≠0 ,“项”和“系数” .启发式、类比法
以教师为主导、学生为主体、问题为主线
问题情景---数学模型-----概念归纳
自主探索、合作交流 教学方法教学方法教学过程教学评价目标分析重、难点教材分析 运用新知 深化概念 归纳小结 反思提高 师生互动 探求新知 布置作业 分层落实 教学方法教学过程教学评价目标分析重、难点教材分析教学过程 创设情景 引入新课 一、创设情境 引入新课问题情境:认识“老朋友” 1、你还记得什么叫方程?什么叫方程的解吗?
2、什么是一元一次方程?它的一般形式是怎样的?
3、我们知道了利用一元一次方程可以解决生活中的一些实际问题,你还记得利用一元一次方程解决实际问题的步骤吗?
创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实问题情境 问题(1) 小区在每两幢楼之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,则绿地的长和宽各为多少?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实问题(2) 学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的年平均增长率?创设情境
导入新课师生互动探求新知运用新知深化概念归纳小结
反思提高布置作业
分层落实(3)一个正方形的面积的2倍等于15,这个正方形的边长是多少?
(4)一个数比另一个数大3,且两个数之积为0,求这两个数。补 充 实 例创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实实 际 问 题
(1)小区在每两幢楼之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,则绿地的长和宽各为多少?
(2) 学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的年平均增长率?
(3)一个正方形的面积的2倍等于15,这个正方形的边长是多少?
(4)一个数比另一个数大3,且两个数之积为0,求这两个数。
二、师生互动 探求新知仔细观察,你会发现什么规律?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实问题:
类比一元一次方程的概念给出一元二次方程的概念:创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实①是整式方程;②只含有一个未知数;③未知数的最高次数是2. 归纳新知,形成概念创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程. 一元二次方程必须同时满足以下三个条件: 观察、思考创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 上述一元二次方程有哪些共同点
和不同点?一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。为什么要限制a≠0,b,c可以为零吗?想一想 a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实三、运用新知 体验成功 1.判断下列方程是否为一元二次方程:创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实 一元二次方程的二次项系数、一次项系数和常数项.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实例:把下面的方程化为一般形式, 并写出它的二次项系数、一次项系数和常数项. 练习:课本P 27练习题1二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实类比学习:
一元二次方程的解(或根).创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实说一说:
未知数的值 x= -1,x=0,x=2
是不是方程 x2-2=x 的根.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实用试验的方法探索情景一中所列方程x(x+10)=900的解,方程有几个解?都是情景一的解吗?四、归纳小结 反思提高
本节课你最大的体验是什么? 本节课你学习了哪些知识? 回
顾
与
思
考本节课你掌握了哪些数学方法?创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实五、布置作业 分层落实2、选做题:
(1)当m取何值时,方程(m-1)x3m+1+2mx+3=0是关于x的一元二次方程?
(3)已知关于x的一元二次方程a(x2-1)-2ax=x(4x-1)+1,写出它的各项系数,并指出字母a的取值范围。
(4)关于x的方程(k-1)(k+3)x2+(k-1)x-k+3=0.当k为何值时,它是一元二次方程?当k为何值时,它是一元一次方程?1、必做题:
(1)P27习题第1、2、3题;
(2)做好下节课学习内容的预习.创设情境
导入新课师生互动探求新知运用新知
深化概念归纳小结
反思提高布置作业
分层落实让数学回归生活教法分析学法分析教学过程教学评价目标分析重难点教材分析1、本节课以以概念讲解为载体,以展示思维分析为主线,重视过程教学,从而发展学生的科学精神和创新意识,培养他们获取知识、运用知识以及运用数学语言进行交流的能力.2、在整个教学过程中,加强数学教学与信息技术教育的整合,借助计算机等多媒体教学手段,加强了学生的感性认识,也有效地激发学生学习数学的兴趣.教 学 评价敬请各位专家、老师
批评指正!再见
华师中山附中 聂少林
