人教版九年级数学二轮专题: 二次函数中倍角的存在性问题解题探究(无答案)
文档属性
| 名称 | 人教版九年级数学二轮专题: 二次函数中倍角的存在性问题解题探究(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 413.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 00:00:00 | ||
图片预览




文档简介
二次函数中倍角的存在性问题解题探究
对于平面直角坐标系中的二倍角问题,往往将其转化成等角问题。对于等角问题,往往有以下解决路径:
(1)将等角转化在一个三角形中,利用等腰三角形两边相等,借助距离公式解决;
(2)用等角的三角比相等,构造直角三角形,寻找比例关系;;
(3)利用角的和差关系,寻找等角,而等角存在两个相似三角形中,往往是子母三角形,利用比例线段构建数量关系;
(4)利用角平分线的相关性质定理。
一、相等角
轴交于点, 其顶点的纵坐标为 4.
(1)求该抛物线的表达式;
(2)求 的正切值;
(3)点在线段的延长线上, 且 , 求 的长.
【解析】解:(1)把点代入得:
当时,
顶点的纵坐标为 4.
故抛物线的表达式为
(2)过点B作交于E点,
令
则
故,
(3)过点D作轴,过点A作,
当点F在CB延长线上,F只能在第四象限,故
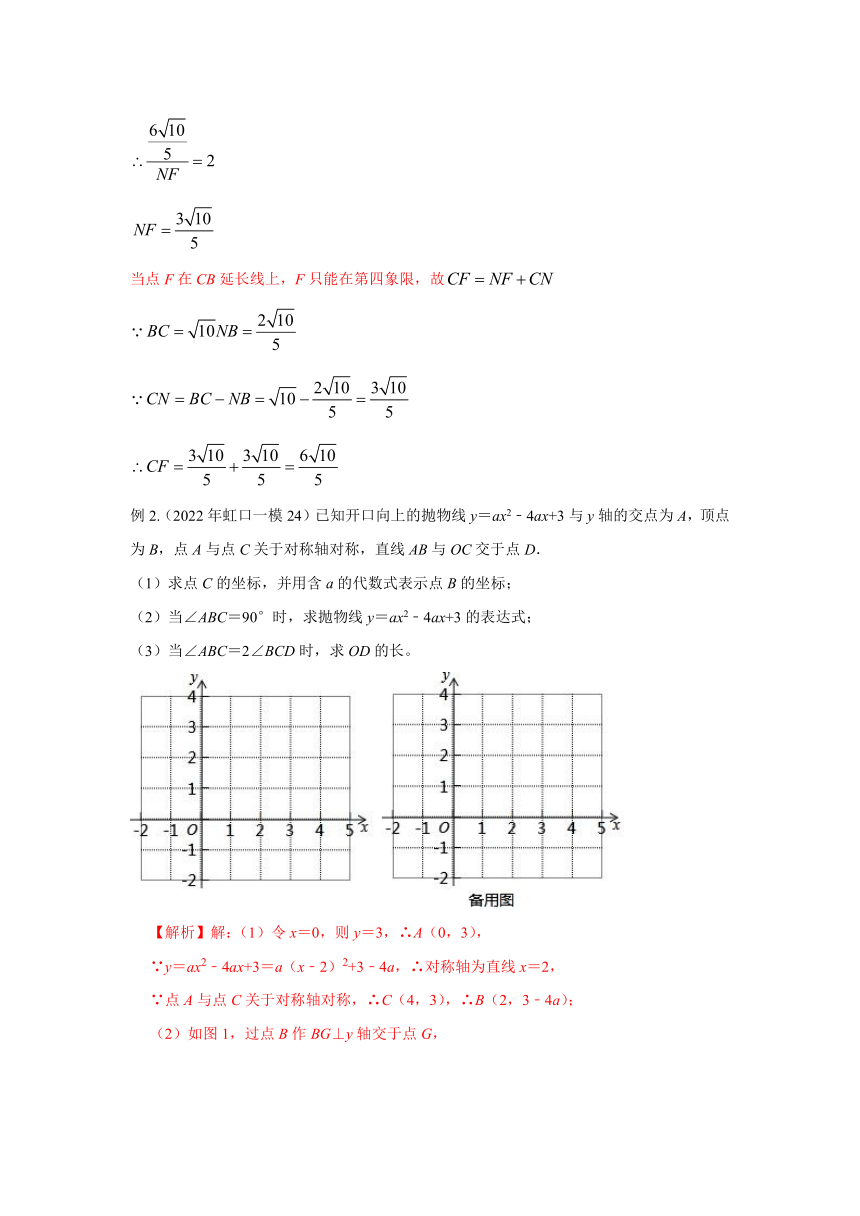
例2.(2022年虹口一模24)已知开口向上的抛物线y=ax2﹣4ax+3与y轴的交点为A,顶点为B,点A与点C关于对称轴对称,直线AB与OC交于点D.
(1)求点C的坐标,并用含a的代数式表示点B的坐标;
(2)当∠ABC=90°时,求抛物线y=ax2﹣4ax+3的表达式;
(3)当∠ABC=2∠BCD时,求OD的长。
【解析】解:(1)令x=0,则y=3,∴A(0,3),
∵y=ax2﹣4ax+3=a(x﹣2)2+3﹣4a,∴对称轴为直线x=2,
∵点A与点C关于对称轴对称,∴C(4,3),∴B(2,3﹣4a);
(2)如图1,过点B作BG⊥y轴交于点G,
∵∠ABC=90°,∴∠OAB=45°,∴AG=BG=2,
∴B(2,1),∴3﹣4a=1,∴a=,∴y=x2﹣2x+3;
(3)如图2,过点B作BH⊥OC交于点H,连接AC,
∵∠ABC=2∠BCD,∴∠NBC=∠CNB,∴∠ONB=2∠OCB,
∵NB∥y轴,∴∠AOC=∠ONB,
∵AC=4,AO=3,∴tan∠AOC=,∴tan∠HNB=,
设HB=4x,则HN=3x,∴NB=5x,∴NB=CN=5x,
∴CH=8x,∴tan∠HCB=,
∵∠OCB=∠NBC=∠ABN,∴=,∴a=1,
∴y=x2﹣4x+3,∴B(2,﹣1),
∵N是OC的中点,∴N(2,),∴BN=,ON=,
∵AO∥BN,∴△AOD∽△BND,
∴=,即=,∴OD=.
练习
1.如图,已知在平面直角坐标系xOy中,直线y=x﹣5与x轴相交于点A,与y轴相交于点B,抛物线y=ax2+6x+c经过A、B两点.
(1)求这条抛物线的表达式;
(2)设抛物线与x轴的另一个交点为C,点P是抛物线上一点,点Q是直线AB上一点,当四边形BCPQ是平行四边形时,求点Q的坐标;
(3)在第(2)小题的条件下,联结QC,在∠QCB内作射线CD与抛物线的对称轴相交于点D,使得∠QCD=∠ABC,求线段DQ的长.
【练习1解析】解:(1)在y=x﹣5中令x=0,得y=﹣5,令y=0得x=5,
∴A(5,0),B(0,﹣5),
将A(5,0),B(0,﹣5)代入y=ax2+6x+c得:
,解得,
∴抛物线的表达式为y=﹣x2+6x﹣5;
(2)在y=﹣x2+6x﹣5中令y=0得x1=1,x2=5,
∴C(1,0),
点P是抛物线上一点,点Q是直线AB上一点,
设P(m,﹣m2+6m﹣5),Q(n,n﹣5),
则BP的中点为(,),CQ的中点为(,),
∵四边形BCPQ是平行四边形,
∴线段BP的中点即是CQ的中点,
∴,
解得或,
∴Q(3,﹣2);
(3)设CD与AB交于N,如图:
∵B(0,﹣5),C(1,0),Q(3,﹣2),
∴CQ=2,BQ=3,
∵∠QCD=∠ABC,∠CQN=∠BQC,
∴△CQN∽△BQC,
∴,即=,
∴QN=,
设N(t,t﹣5),而Q(3,﹣2),
∴=,
∴t=或t=,
∵在∠QCB内作射线CD,
∴t=,N(,﹣),
设CN解析式为y=kx+b,将N(,﹣),C(1,0)代入得:
,解得,
∴CN解析式为y=﹣5x+5,
令x=3得y=﹣10,
∴Q(3,﹣10),
∴DQ=﹣2﹣(﹣10)=8.
如图,抛物线经过,两点,与y轴交于点C,P为第四象限内抛物线上一点,过点P作PM⊥x轴于点M,连接AC,AP,AP与y轴交于点D.
(1)求抛物线的函数表达式.
(2)当∠MPA=2∠PAC时,求直线AP的函数表达式.
(3)在(2)的条件下,在抛物线的对称轴上是否存在点E,使以E,M,C为顶点的三角形是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)
解:把,分别代入,得.
解得.
∴抛物线的函数表达式为;
(2)
解:根据题意,得.
∴∠MPA=∠ODA.
又∵∠MPA=2∠PAC,∴∠ODA=2∠PAC.
又∵∠ODA=∠DAC+∠ACD,
∴∠DAC=∠ACD.∴CD=AD.
在中,令,解得,∴.
设OD=m,则AD=CD=3-m.
∵,∴OA=1.
在Rt△AOD中,根据勾股定理,得.解得.
∴.
设直线AP的函数表达式为.
把,分别代入,得解得
∴直线AP的函数表达式为;
(3)
解:存在,点E的坐标为或或或.
令,解得,.
∴点P的横坐标为.
∵PM⊥x轴,∴.
由,得抛物线的对称轴为直线,
由(2)可得.
设点E的坐标为,则,,.
若∠MCE=90°,则,即,解得.
若∠CME=90°,则,即,解得.
若∠CEM=90°,则,即,解得,.
综上所述,点E的坐标为或或或.
【点睛】本题考查的是二次函数的综合题,熟练掌握二次函数的图像与性质,直角三角形的性质是解决问题的关键.
综合与探究
如图,抛物线y= x2+x+4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求A,B,C三点及抛物线顶点的坐标;
(2)点D是抛物线上的一个动点,设点D的横坐标为m(0(3)试探究:在y轴上是否存在点P,使得∠PAO=∠ABC,若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)
解:将y=0代入y= x2+x+4,得0= x2+x+4.
解得:x1= 1,x2=3.
∴A( 1,0),B(3,0).
将x=0代入y= x2+x+4,得y=4.
∴C(0,4).
∵y= x2+x+4= (x 1) 2+,
∴抛物线顶点坐标为(1,);
(2)
解:过点D作DM∥y轴,交BC于点M.
设直线BC的函数表达式为y=kx+b.
将B(3,0),C(0,4)代入y=kx+b,
得解得,
∴直线BC的函数表达式为y= x+4.
∵点D在抛物线上,
∴D(m, m2+m+4).
∵DM∥y轴,
∴M(m, m+4).
∵S△CBD=S△CMD+S△BMD=DM |xB xC|=DM,
∴当DM最大时,S△CBD最大.
∵DM=( m2+m+4) ( m+4)= m2+4m= (m )2+3.
∵ <0,
∴当△CBD的面积最大时,m的值为;
(3)
解:∵B(3,0),C(0,4),
∴OB=3,OC=4,
∴BC==5,
作BN平分∠OBC交OC于点N,过点N作NE⊥BC于点E,
∵NO⊥OB,NE⊥BC,BN平分∠OBC,
∴NO= NE,
∴,
∵,
∴,
又∵CN+ON=OC=4,
∴CN=,ON=,
∵∠P1AO=∠ABC=∠NBO,∠P1OA=∠NOB=90°,
∴△P1OA∽△NOB,
∴,即,
∴P1O=,
同理求得P2O=,
∴P1(0,),P2(0,-) .
【点睛】本题是二次函数的综合题,熟练掌握二次函数的图像及性质,角平分线的性质,相似三角形的判定和性质,分类讨论是解题的关键.
对于平面直角坐标系中的二倍角问题,往往将其转化成等角问题。对于等角问题,往往有以下解决路径:
(1)将等角转化在一个三角形中,利用等腰三角形两边相等,借助距离公式解决;
(2)用等角的三角比相等,构造直角三角形,寻找比例关系;;
(3)利用角的和差关系,寻找等角,而等角存在两个相似三角形中,往往是子母三角形,利用比例线段构建数量关系;
(4)利用角平分线的相关性质定理。
一、相等角
轴交于点, 其顶点的纵坐标为 4.
(1)求该抛物线的表达式;
(2)求 的正切值;
(3)点在线段的延长线上, 且 , 求 的长.
【解析】解:(1)把点代入得:
当时,
顶点的纵坐标为 4.
故抛物线的表达式为
(2)过点B作交于E点,
令
则
故,
(3)过点D作轴,过点A作,
当点F在CB延长线上,F只能在第四象限,故
例2.(2022年虹口一模24)已知开口向上的抛物线y=ax2﹣4ax+3与y轴的交点为A,顶点为B,点A与点C关于对称轴对称,直线AB与OC交于点D.
(1)求点C的坐标,并用含a的代数式表示点B的坐标;
(2)当∠ABC=90°时,求抛物线y=ax2﹣4ax+3的表达式;
(3)当∠ABC=2∠BCD时,求OD的长。
【解析】解:(1)令x=0,则y=3,∴A(0,3),
∵y=ax2﹣4ax+3=a(x﹣2)2+3﹣4a,∴对称轴为直线x=2,
∵点A与点C关于对称轴对称,∴C(4,3),∴B(2,3﹣4a);
(2)如图1,过点B作BG⊥y轴交于点G,
∵∠ABC=90°,∴∠OAB=45°,∴AG=BG=2,
∴B(2,1),∴3﹣4a=1,∴a=,∴y=x2﹣2x+3;
(3)如图2,过点B作BH⊥OC交于点H,连接AC,
∵∠ABC=2∠BCD,∴∠NBC=∠CNB,∴∠ONB=2∠OCB,
∵NB∥y轴,∴∠AOC=∠ONB,
∵AC=4,AO=3,∴tan∠AOC=,∴tan∠HNB=,
设HB=4x,则HN=3x,∴NB=5x,∴NB=CN=5x,
∴CH=8x,∴tan∠HCB=,
∵∠OCB=∠NBC=∠ABN,∴=,∴a=1,
∴y=x2﹣4x+3,∴B(2,﹣1),
∵N是OC的中点,∴N(2,),∴BN=,ON=,
∵AO∥BN,∴△AOD∽△BND,
∴=,即=,∴OD=.
练习
1.如图,已知在平面直角坐标系xOy中,直线y=x﹣5与x轴相交于点A,与y轴相交于点B,抛物线y=ax2+6x+c经过A、B两点.
(1)求这条抛物线的表达式;
(2)设抛物线与x轴的另一个交点为C,点P是抛物线上一点,点Q是直线AB上一点,当四边形BCPQ是平行四边形时,求点Q的坐标;
(3)在第(2)小题的条件下,联结QC,在∠QCB内作射线CD与抛物线的对称轴相交于点D,使得∠QCD=∠ABC,求线段DQ的长.
【练习1解析】解:(1)在y=x﹣5中令x=0,得y=﹣5,令y=0得x=5,
∴A(5,0),B(0,﹣5),
将A(5,0),B(0,﹣5)代入y=ax2+6x+c得:
,解得,
∴抛物线的表达式为y=﹣x2+6x﹣5;
(2)在y=﹣x2+6x﹣5中令y=0得x1=1,x2=5,
∴C(1,0),
点P是抛物线上一点,点Q是直线AB上一点,
设P(m,﹣m2+6m﹣5),Q(n,n﹣5),
则BP的中点为(,),CQ的中点为(,),
∵四边形BCPQ是平行四边形,
∴线段BP的中点即是CQ的中点,
∴,
解得或,
∴Q(3,﹣2);
(3)设CD与AB交于N,如图:
∵B(0,﹣5),C(1,0),Q(3,﹣2),
∴CQ=2,BQ=3,
∵∠QCD=∠ABC,∠CQN=∠BQC,
∴△CQN∽△BQC,
∴,即=,
∴QN=,
设N(t,t﹣5),而Q(3,﹣2),
∴=,
∴t=或t=,
∵在∠QCB内作射线CD,
∴t=,N(,﹣),
设CN解析式为y=kx+b,将N(,﹣),C(1,0)代入得:
,解得,
∴CN解析式为y=﹣5x+5,
令x=3得y=﹣10,
∴Q(3,﹣10),
∴DQ=﹣2﹣(﹣10)=8.
如图,抛物线经过,两点,与y轴交于点C,P为第四象限内抛物线上一点,过点P作PM⊥x轴于点M,连接AC,AP,AP与y轴交于点D.
(1)求抛物线的函数表达式.
(2)当∠MPA=2∠PAC时,求直线AP的函数表达式.
(3)在(2)的条件下,在抛物线的对称轴上是否存在点E,使以E,M,C为顶点的三角形是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)
解:把,分别代入,得.
解得.
∴抛物线的函数表达式为;
(2)
解:根据题意,得.
∴∠MPA=∠ODA.
又∵∠MPA=2∠PAC,∴∠ODA=2∠PAC.
又∵∠ODA=∠DAC+∠ACD,
∴∠DAC=∠ACD.∴CD=AD.
在中,令,解得,∴.
设OD=m,则AD=CD=3-m.
∵,∴OA=1.
在Rt△AOD中,根据勾股定理,得.解得.
∴.
设直线AP的函数表达式为.
把,分别代入,得解得
∴直线AP的函数表达式为;
(3)
解:存在,点E的坐标为或或或.
令,解得,.
∴点P的横坐标为.
∵PM⊥x轴,∴.
由,得抛物线的对称轴为直线,
由(2)可得.
设点E的坐标为,则,,.
若∠MCE=90°,则,即,解得.
若∠CME=90°,则,即,解得.
若∠CEM=90°,则,即,解得,.
综上所述,点E的坐标为或或或.
【点睛】本题考查的是二次函数的综合题,熟练掌握二次函数的图像与性质,直角三角形的性质是解决问题的关键.
综合与探究
如图,抛物线y= x2+x+4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求A,B,C三点及抛物线顶点的坐标;
(2)点D是抛物线上的一个动点,设点D的横坐标为m(0
(1)
解:将y=0代入y= x2+x+4,得0= x2+x+4.
解得:x1= 1,x2=3.
∴A( 1,0),B(3,0).
将x=0代入y= x2+x+4,得y=4.
∴C(0,4).
∵y= x2+x+4= (x 1) 2+,
∴抛物线顶点坐标为(1,);
(2)
解:过点D作DM∥y轴,交BC于点M.
设直线BC的函数表达式为y=kx+b.
将B(3,0),C(0,4)代入y=kx+b,
得解得,
∴直线BC的函数表达式为y= x+4.
∵点D在抛物线上,
∴D(m, m2+m+4).
∵DM∥y轴,
∴M(m, m+4).
∵S△CBD=S△CMD+S△BMD=DM |xB xC|=DM,
∴当DM最大时,S△CBD最大.
∵DM=( m2+m+4) ( m+4)= m2+4m= (m )2+3.
∵ <0,
∴当△CBD的面积最大时,m的值为;
(3)
解:∵B(3,0),C(0,4),
∴OB=3,OC=4,
∴BC==5,
作BN平分∠OBC交OC于点N,过点N作NE⊥BC于点E,
∵NO⊥OB,NE⊥BC,BN平分∠OBC,
∴NO= NE,
∴,
∵,
∴,
又∵CN+ON=OC=4,
∴CN=,ON=,
∵∠P1AO=∠ABC=∠NBO,∠P1OA=∠NOB=90°,
∴△P1OA∽△NOB,
∴,即,
∴P1O=,
同理求得P2O=,
∴P1(0,),P2(0,-) .
【点睛】本题是二次函数的综合题,熟练掌握二次函数的图像及性质,角平分线的性质,相似三角形的判定和性质,分类讨论是解题的关键.
同课章节目录
